多重不确定性需求下多产品订单相似性研究

张青山， 刘岩峰，2， 徐 伟

(1. 沈阳工业大学 管理学院， 沈阳 110870； 2. 渤海大学 管理学院， 辽宁 锦州 121013)

用户需求的不确定性，使得其对于装备制造企业的产品需求也不相同。这种不确定性包括产品品种不确定、数量不确定、质量不确定、交货期不确定等。由于客户订单的不确定性以及各种情况的发生，虽然客户需求的产品品种不同，需求的时间、数量、质量以及交货期等都不相同，但是这些订单需求存在一定的相似性，如果能找到它们之间的相似性，就可以把相似性大的订单进行并单处理或者组合处理。这样就能有效地利用有限的资源满足各种复杂的订单需求，同时也可节省大量时间成本和生产成本。因此，研究不确定需求下订单相似性十分必要，可以对出现相似性的订单需求进行相似性智能处理，从而方便企业制定生产计划或者修改、取消计划，并制定出相应的订单排产策略。

针对制造企业订单相似性，很多学者和专家都进行了相应的工作和研究。韩文民等(2018)研究了紧急订单下序位相似性问题[1]。张于贤等(2018)研究了多品种小批量的产品交货期和加工工艺相似性订单成组问题[2]。吴天行等(2017)基于巷道相似性和通道相似性研究了订单分批问题[3-4]。陈俊等(2017)建立了产品质量属性相似度模型和优化方法[5]。程贤福等(2017)研究了产品相似性等方面的适应性指标[6]。徐新胜等(2016)提出了解决产品结构相似性的判断方法[7]。胡小林等(2019)研究了需求不均衡下拣选截止时间和通道的相似性[8]。禹春霞等(2019)为了满足用户需求，研究了用户与候选服务商的相似性[9]。李若岩等(2019)采用模糊数学聚类法分析青海石脑油相似性[10]。施伟锋等(2019)采用模糊C均值聚类算法分析属性空间相似性[11]。王永泉等(2019)采用模糊聚类多层次分析法研究了零件间加工工艺相似性[12]。张青山等(2018)研究了双渠道采购模式下装备制造业选址生产问题[13]。韩世莲(2016)研究了可以满足多种客户需求属性的模糊系统聚类方法[14]。岳文军(2015)采用RSCF分析法分析了订单的相似性等特征对物流体系的影响[15]。

虽然很多学者对于产品或订单相似性进行研究，但是没有从需求的角度分析，研究在多重不确定需求的情况下订单相似性问题。虽然有研究订单的交货期、工艺路线和数量，但是没有将各种情况进行综合研究。本文针对装备制造企业多品种生产中基于多重不确定性需求的产品订单相似性进行分析。

一、问题描述与分析

假设装备制造企业共有N种产品，某段时间内有H个产品订单需求，UncertainDemandh表示某一时刻的需求，包括需求到达的时间、需求的品种、需求的数量、需求的质量和需求的交货日期等，具体可表示为UncertainDemandh=(DNh，DVh，DQh，DWh，DTh，PSh)。式中：h=1，2，…，H；DNh表示第h订单需求到达的时间，其取值为0，1，2，…的非负整数，假设为随机离散变量；DVh表示为第h订单需求的产品品种，其取值为1，2，…，N，N+1的正整数，假设为随机离散变量；DQh表示第h订单需求的需求数量，其取值为正整数或者为批量的倍数，假设为随机离散变量；DWh表示第h订单需求的质量需求，假设为模糊区间需求；DTh表示订单交货期需求，假设交货期需求为模糊区间需求；PSh表示订单需求的情景，取值为：PSh=1表示正常订单，PSh=2表示紧急订单，PSh=3表示修改订单。不确定需求的构成如表1所示。

表1 不确定需求的构成

二、具有多重不确定性需求的装备制造企业多产品订单相似性模型

对于产品的相似性.主要是考虑产品加工工艺的相似性。对于装备制造企业来说，可以利用加工工艺的工序步骤来区分不同品种产品的相似性。对产品的细化，可以根据组件或者部件相似性来定义。产品相似性主要是由部件组成，包括组成部件的种类、部件的相似性、组件个数和产品组装工艺。而产品组件的相似性由部件或组件的加工工艺、加工生产车间、加工时间等来定义。

1. 产品品种的相似性

设装备制造企业的工件或组件有M个，Componentm表示第m个工件或组件。假设装备制造企业共有Z个加工工序，则Processz表示第z个加工工序，并设ProcessNoz=z，z=1，2，…，Z，具体如表2所示。

表2 工序内容信息

设第m个工件或组件需要加工OPNumberm个工序，用OPm(g)表示第m个组件的第g个加工工序，则

OPm(g)=ProcessNoz(z=1，2，…，Z)

(1)

另外，设第m个工件或组件Componentm的加工工艺路线为Routingm，设其包括RoutingNumberm个工序，则

Routingm=OPm(1)→OPm(2)→ … →

OPm(OPNumberm)

(2)

则企业的工件或组件的内容信息构成如表3所示。

表3 工件或组件的内容信息

根据文献[16]的工序相似性算法计算组件的相似性距离，记为Distance(m1，m2)，假设m1≠m2，表示工件或组件m2到工件或组件m1的加工工艺相似性距离。

计算工件或组件加工的步骤如下：

(1) 以m1组件为基准，对于其每一个工序i=1，2，…，RoutingNumberm1计算其在m2组件工序中的序号，用PosNumi(m1，m2)表示m1组件第i个工序OPm1(i)在m2组件工序Routingm2中的序号。如果m1组件的OPm1(i)在m2组件工序中则得到其序号，否则记为0。

(2) 对于步骤(1)中序号PosNumi(OPm1(i)，Routingm)之间的距离则有

(3)

其中：i=1，2，…，RoutingNumberm1-1

(3) 组件的相似性距离

RoutingNumberm1+1

(4)

则构建组件间相似性距离M×M方形矩阵，组件间相似性距离如表4所示。

由表4可知，以组件中距离最远的组件与该行组件最不相似，距离最近的组件与该行组件最为相似。

表4 组件间相似性距离

假设similiar(i，j)表示组件组件i到j的相似性，则

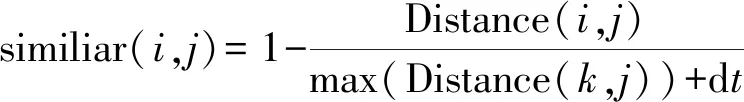
(5)

式中，dt是产品相似性偏移量。

本文采用取平均值最小的行所在的组件作为基准组件，以该组件为对比组件计算组件的相似性。假设取的平均值最小的行号为minLine，则组件相似性为similiar(minLine，j)，其中j=1，2，…，M。

2. 产品需求的聚类分析

首先，由于表1中多重不确定性需求的各项数据单位并不一致，所以需要进行归一化处理，可以采用如下处理：

DNh取最低值为1，其他值为与该最低值的比值；DVh取最低值为1，其他值为与该最低值的比值；DQh取最低值为1，其他值为与该最低值的比值；DWh采用三角模糊进行处理，然后取模糊数最低值为1，其他值为与该最低值的比值；DTh采用梯形模糊进行处理，然后取模糊数最低值为1，其他值为与该最低值的比值；PSh以正常订单为1，其他值为与该最低值的比值。

对UncertainDemandh进行归一化处理。采用组件相似性为similiar(minLine，j)对产品种类DVh进行归一化处理。到达时间DNh和交货期DTh取最小的时间为1，其他值为与该最低值的比值。设归一化后的矩阵UncertainDemand′={UncertainDemand′1，UncertainDemand′2，…，Uncertain-Demand′h}，其中UncertainDemand′h={DN′h，DV′h，DQ′h，DW′h，PS′h}表示第h=1，2，…，H个需求。

对于UncertainDemand′具有H个订单需求，假设将这H个订单需求分成type_num(2≤type_num≤H)个类别，则UncertainDemand′被分成{SK1，SK2，…，SKtype_num}的type_num个类别，U为相似分类值，并设各类别的聚类中心为{center1，center2，…，centertype_num}，设μhk为订单需求Uncertain-Demand′h对于SKk的隶属度，则可以将目标函数Jb表示为

(6)

dhk=d(UncertainDemand′h-centerk)=

(7)

式中：dhk表示第h个订单需求UncertainDemand′h与SKk的欧几里得距离；m为订单需求的特征数；b为加权参数，其取值为1≤b≤∞。

为寻找一个最佳的分类，模糊C-均值聚类方法(FCM)要求该订单需求对于类别的隶属度值和为1，从而产生最小的函数值Jb，即满足

(8)

利用式(5)、(6)来分别计算订单需求Uncertain-Demand′h对于SKk的隶属度μhk和type_num个聚类中心{centerk}，则有

(9)

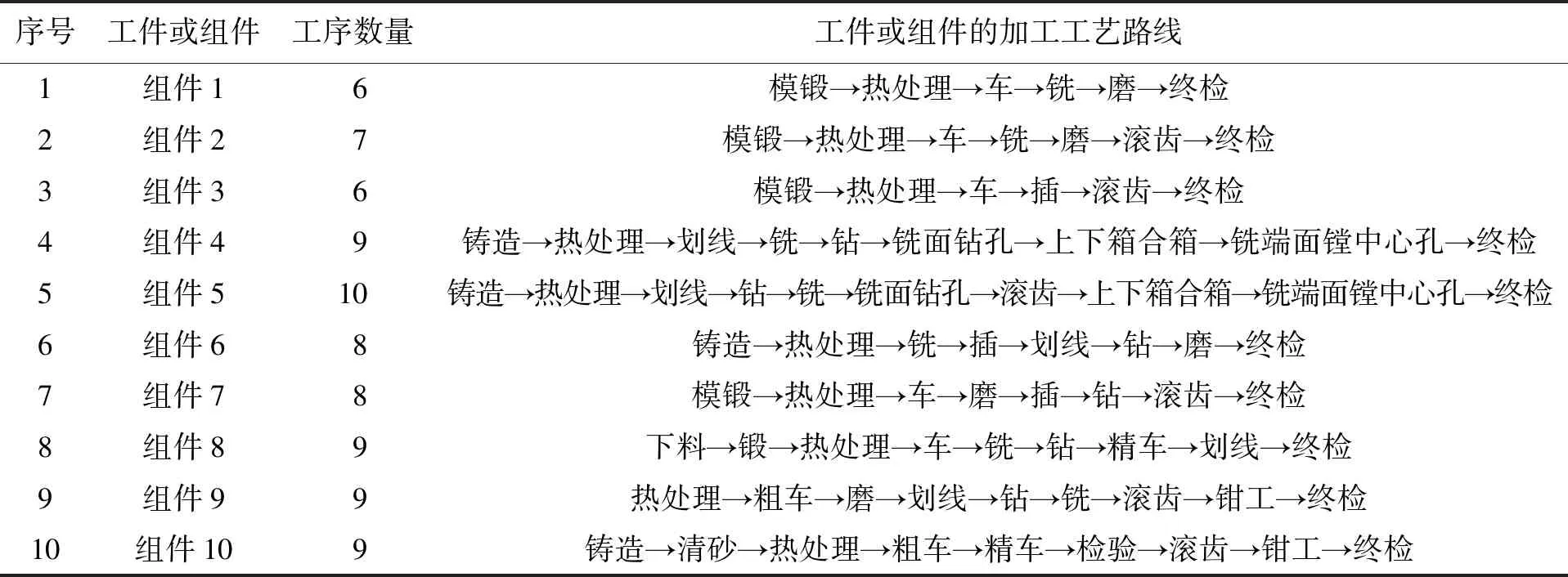
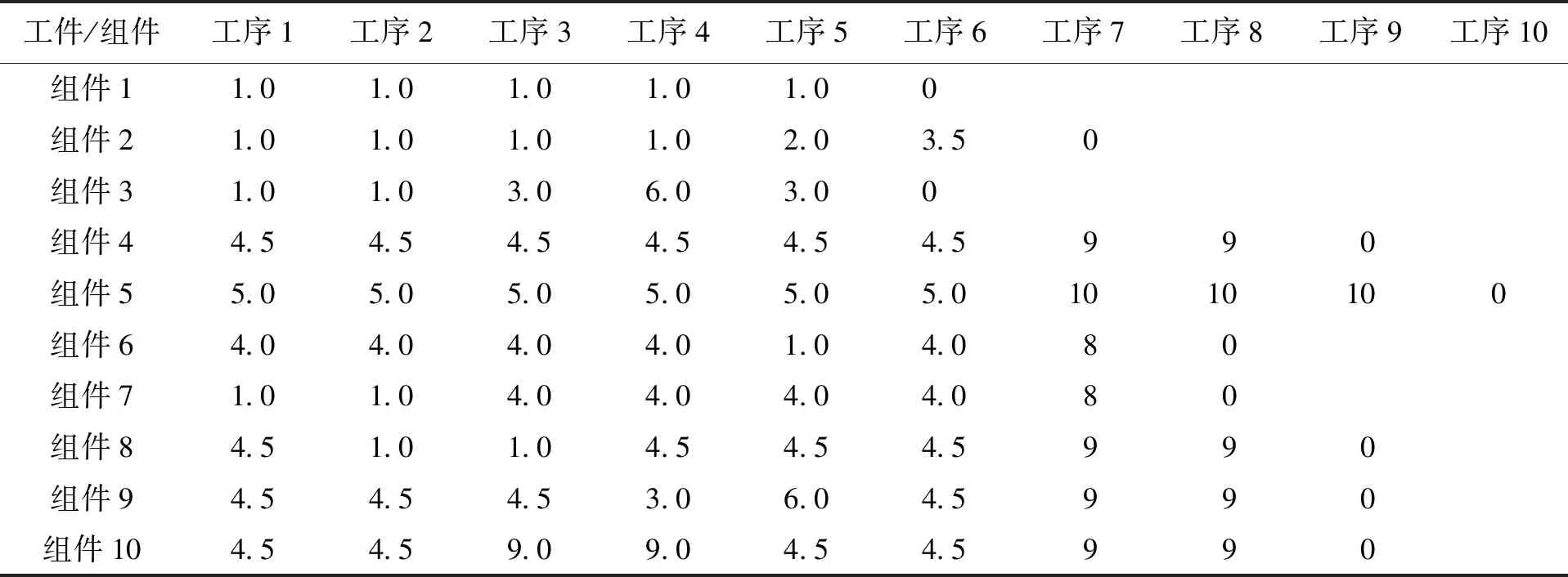
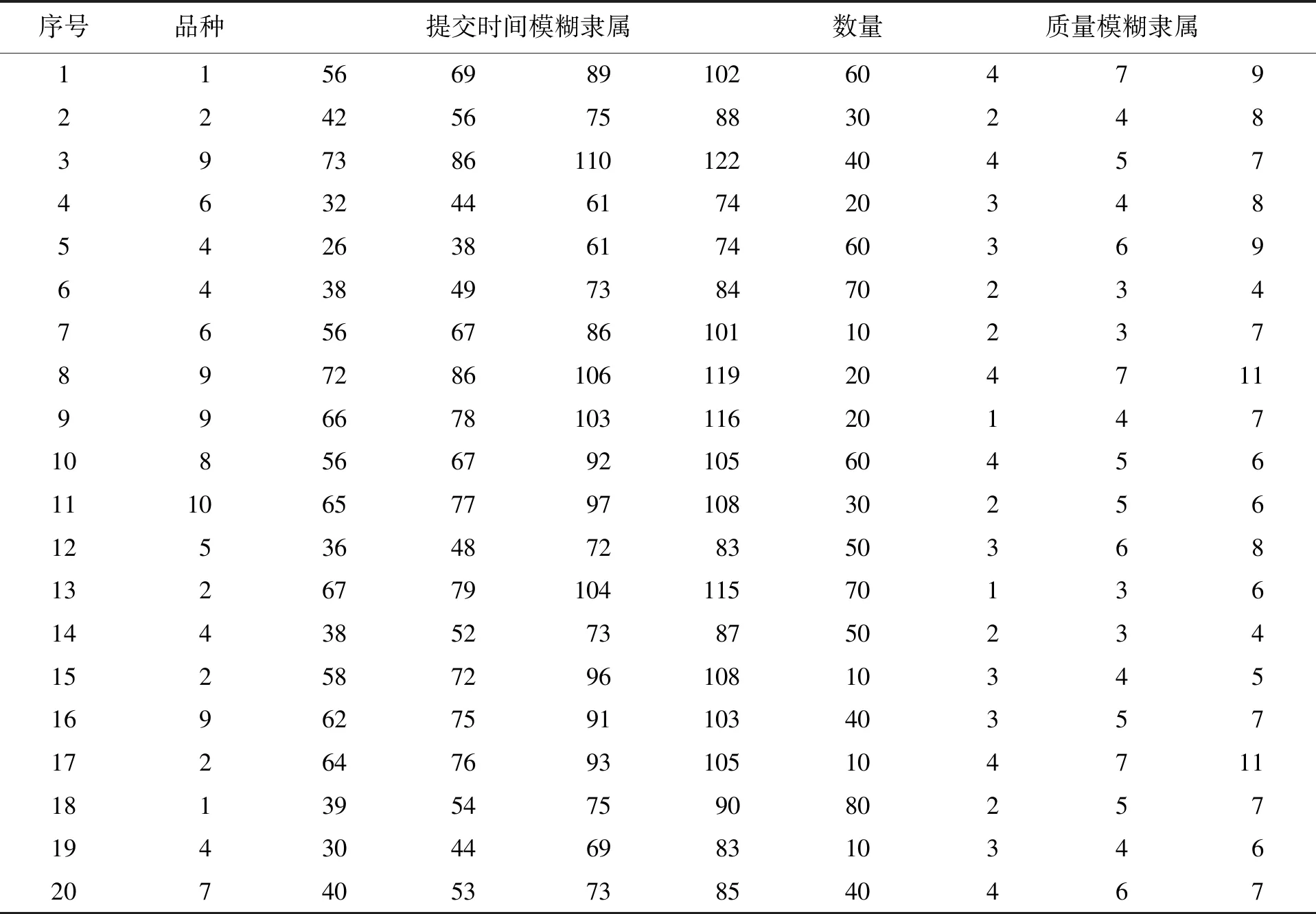
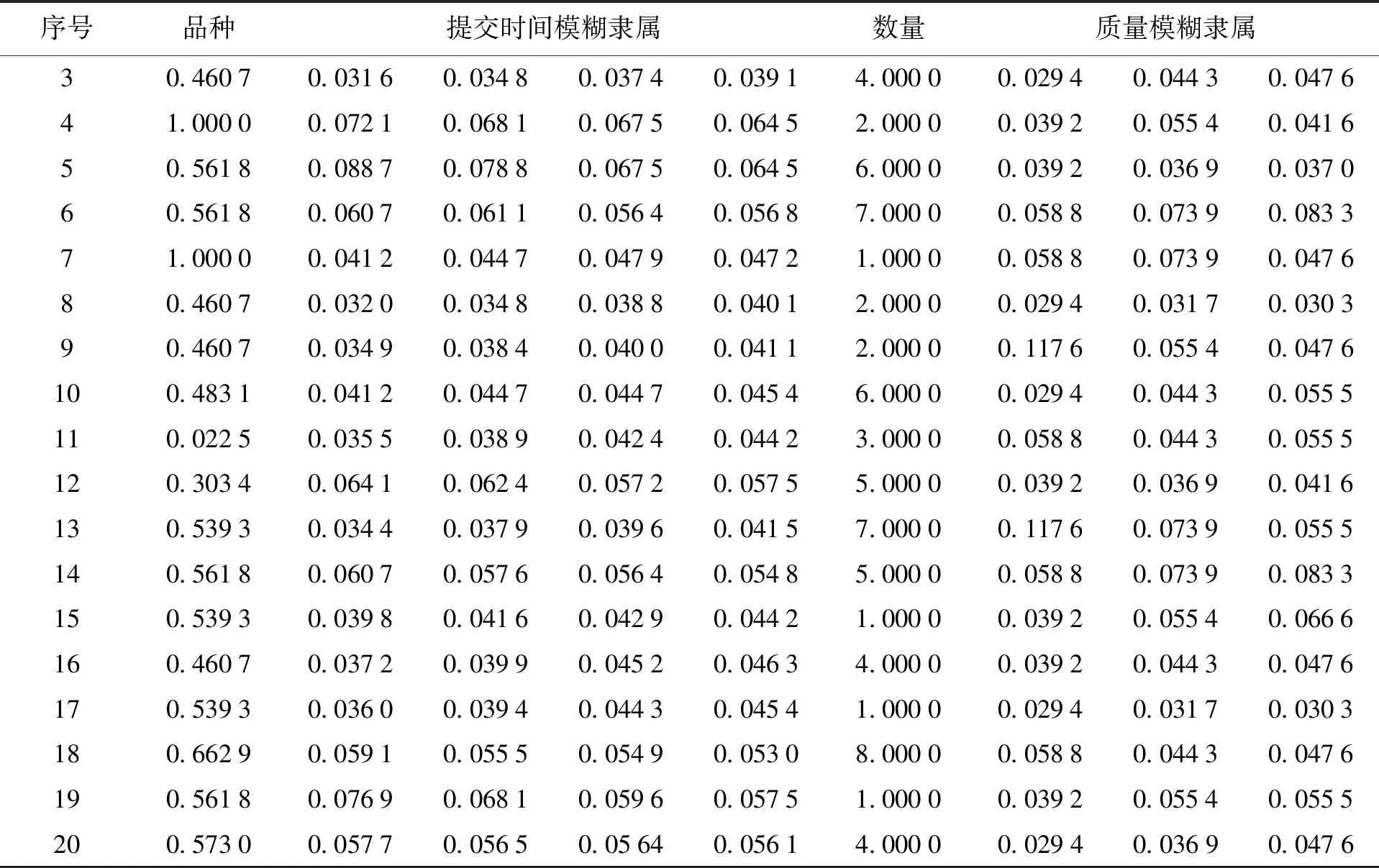
设Hk={h|2≤type_num

(10)

利用式(7)、(8)重复修改{center1，center2，…，centertype_num}、μhk和分类。当算法收敛时模糊聚类结束，从而获得各类别的{center1，center2，…，centertype_num}以及μhk。

三、算例分析

假设某装备制造企业工件或组件有10个，Componentm表示的是第m个工件或组件。假设装备制造企业共有Z个加工工序，则Processz表示第z个加工工序，并设ProcessNoz=z，z=1，2，…，Z。设第m个工件或组件需要加工OPNumberm个工序，用OPm(g)表示第m个组件的第g个加工工序。工件或组件加工工艺如表5所示。

表5 工件或组件加工工艺

计算PosNumi(m1，m2)来表示m1组件第i个工序OPm1(i)在m2组件工序Routingm2中的序号，并以每个组件为基准计算每个组件的Pos-Numi(m1，m2)。表6为以m1=组件1为基准的每个组件的位置号，其他限于篇幅不一一列举。

表6 以m1=组件1为基准的每个组件的位置号PosNumi(1，m2)

计算组件i到组件j的相似性距离，结果如表7所示。

计算组件i到j的相似性，其中产品相似性偏移量dt=1，结果如表8所示。

表7 组件间相似性距离

表8 组件间工艺相似性距离

将平均值最小的行所在的组件作为基准组件，即组件6，以其为对比组件计算组件的相似性。假设取平均值最小的行号为minLine=6，则组件相似性如表9所示。

假设某装备制造企业的客户需求如表10所示。进行归一化处理，结果如表11所示。

表9 组件的工艺相似性

表10 某装备制造企业的客户需求

表11 某装备制造企业的客户需求归一化处理

表11(续)

采用模糊C-均值聚类算法(FMC)对需求进行聚类。可以将20组需求按序号如下的方法进行聚类：第一类为2、8、9、11；第二类为1、5、6、10、13、18；第三类为3、12、14、16、20；第四类为4、7、15、17、19。

运行之后得到的目标函数值Jb=2.064 8，而且每次运行结果都不一样。这跟初始聚类中的中心点有关系，其中某次聚类结果如图1所示，三角形为各类的聚类中心点。

图1 多产品订单需求模糊C-均值聚类

四、结 语

本文根据产品组件的加工工艺过程进行相似性分析，找到相似性基准组件，并计算各组件之间的相似性。同时，针对订单需求的多重不确定性，包括品种、数量、交货期、质量等，采用模糊C-均值聚类算法对订单需求进行聚类。采用算例对产品订单需求的相似性进行分析，能够解决现实中的订单分组或成组生产问题。未来对相似订单排产问题可以进行进一步研究。