拟Clifford半环的性质与结构

韩 姣 李 刚

(山东师范大学数学与统计学院,250358,济南)

1 引言及预备知识

半环是具有加法和乘法两个代数运算且满足结合律、分配律的代数系.半环的概念最早是在1894年由Dedekind提出来的，如今半环理论已经广泛运用到泛函分析、拓扑学及计算机科学等领域，近年来，许多代数学者对半环的结构进行了深入的研究并取得了很多有意义的研究成果.

称半环S=(S,+,·)为幂等元半环，若∀(a∈S)a+a=a·a=a.文献[1]介绍了一类重要的幂等元半环—带半环，一个幂等元半环S=(S,+,·)称为带半环，若对∀a,b∈S，

a+ab+a=a，

a+ba+a=a.

一个带半环S=(S,+,·)称为T半环，若S的加法半群(S,+)是一个T带，其中T可能是“矩形”、“左(右)零”、“左(右)正则”、“正则”、“正规”带等等.

本文定义了拟Clifford半环，它是左(右)Clifford半环、矩形Clifford半环的推广，给出了一个半环是拟Clifford半环的充要条件及拟Clifford半环的织积分解.

引理1[2]若S是纯整群，则∀a,b∈S,V+(b)+V+(a)⊆V+(a+b).

引理2[2]关于半群S下列条件等价：

(i)S是一个左群；

(ii)S是正则的且E(S)是左零半群；

(iii)S≅L×G,其中L是左零半群，G是群.

引理3[3]关于半群S下列条件等价：

(i)S是一个左Clifford半群；

(ii)S是左群的半格.

同样对于右Clifford半群有类似的结论.

定义1[4]纯整群S称为拟Clifford半群，若E(S)是正则带.

因为纯整群是矩形群的半格，所以若S是拟Clifford半群，则S是矩形群的半格且E(S)是正则带.

定理1[4]半群S是拟Clifford半群的充分必要条件是S同构于织积Sl×TSr,其中Sl=[Y;Lα×Tα]是左Clifford半群，Sr=[Y;Tα×Rα]是右Clifford半群，且在半群同态Φ:(i,x)x，∀(i,x)∈Sl与Ψ:(x,λ)x，∀(x,λ)∈Sr下它们有相同的Clifford半群分量T=[Y;Tα].

引理4[5]若S是加法半群为完全正则半群的半环，则

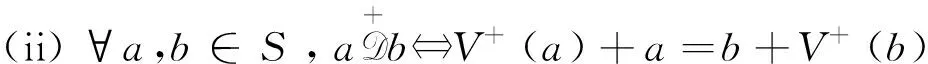
定义2[6]一个半环S称为左环，若S是一个左零带半环和一个环的直积.

定理2[6]一个半环是左环的充分必要条件是：

(i)S的加法半群(S,+)是一个左交换群，即是一个左零带和一个交换群的直积；

(ii)E+(S)⊆E·(S)其中E+(S)(E·(S))表示S的加法(乘法)半群的幂等元的集合.

定义3[6]一个半环S称为左Clifford半环，若S是左环的分配格.

定义4[5]一个半环S称为矩形环，若S是一个矩形带半环和一个环的直积.

定理3[5]一个半环S是矩形环的充分必要条件是：

(i)S的加法半群(S,+)是一个矩形交换群，即是一个矩形带和一个交换群的直积；

(ii)E+(S)⊆E·(S)其中E+(S)(E·(S))表示S的加法(乘法)半群的幂等元的集合.

定义5[6]一个半环S称为矩形Clifford半环，若S是矩形环的分配格.

2 拟Clifford 半环的定义与性质

定义6[7,8]一个半环S称为拟Clifford半环，若S是矩形环的分配格，并且E+(S)是一个正则带.

定理4半环S是拟Clifford半环的充分必要条件是S的加法半群(S,+)是拟Clifford半群，其极大子群是可交换的，E+(S)⊆E·(S)，并且S满足以下条件：

(i) ∀a∈S,V+(a)+a⊇a(a+V+(a))；

(ii) ∀a,b∈S,V+(ab)+ab⊇(b+V+(b))a；

(iii) ∀a,b∈S,V+(a)+a⊇a+ab+V+(ab)+V+(a).

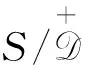
a2+ax+a2=a(a+x+a)=aa=a2；

ax+a2+ax=a(x+a+x)=ax.

所以aV+(a)⊆V+(a2)，从而由引理4知

V+(a)+a=a2+V+(a2)⊇a2+aV+(a)=a(a+V+(a))，

即

∀a∈S,V+(a)+a⊇a(a+V+(a)).

(1)

同样的，由引理4知

V+(ab)+ab=ba+V+(ba)⊇ba+V+(b)a=(b+V+(b))a，

即

∀a,b∈S,V+(ab)+ab⊇(b+V+(b))a.

(2)

又因为(S,+)是纯整群，所以∀a,b∈S,V+(a+b)⊇V+(b)+V+(a)，因此由引理4得

V+(a)+a=a+ab+V+(a+ab)⊇(a+ab)+V+(ab)+V+(a)，

∀a,b∈S,V+(a)+a⊇a+ab+V+(ab)+V+(a).

(3)

(a2+V+(a2)∩(V+(a)+a)⊇a(a+V+(a))，

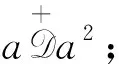
因为∀a,b∈S,ba+V+(ba)⊇ba+V+(b)a=(b+V+(b))a，由S满足条件(ii)得

(ba+V+(ba)∩(V+(ba)+ab)⊇(b+V+(b))a，

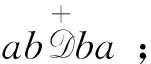
因为∀a,b∈S,a+ab+V+(a+ab)⊇a+ab+V+(ab)+V+(a)，所以由S满足条件(iii)得

(a+ab+V+(a+ab))∩(V+(a)+a)⊇a+ab+V+(ab)+V+(a)，

在上述定理中，通过式子(2)我们知道对∀a,b∈S,V+(ab)+ab⊇a(V+(b)+b)，由此可得E+(S)是(S,·)上的理想.

3 拟Clifford 半环的织积结构

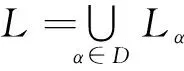
∀(i,x)∈Sl与Ψ:(x,λ)x，∀(x,λ)∈Sr下它们有相同的半环Clifford分量T=[D;Tα].

证充分性.若S同构于织积Sl×TSr，其中(Sl,+)=[D;(Lα,+)×(Tα,+)]是左Clifford半群，(Sr,+)=[D;(Tα,+)×(Rα,+)]是右Clifford半群且它们在同态Φ:(i,x)x，∀(i,x)∈(Sl,+)与Ψ:(x,λ)x，∀(x,λ)∈(Sr,+)下具有相同的Clifford半群分量(T,+)=[D;(Tα,+)],则(S,+)=(Sl,+)×T(Sr,+),E+(S)=E+(Sl)×TE+(Sr),其中E+(Sl)=[D;(Iα,+)×{1(Tα,+)}]，E+(Sr)=[D;{1(Tα,+)}×(Rα,+)]，则E+(S)是正则带.对∀((i,x),(x,λ))∈Sl×Sr，记((i,x),(x,λ))=(i,x,λ).易证S是矩形环Lα×Tα×Rα的分配格，因为E+(S)是正则带，因此S是拟Clifford半环.由引理5得是左Clifford半环Sl和右Clifford半环Sr上的半环同余，所以是(S,+)上的同余.

的织积，其中(Lα,+)是左零带，(Tα,+)是交换群，(Rα,+)是右零带，并且它们在半群同态Φ:(i,x)x，∀(i,x)∈(Sl,+)与Ψ:(x,λ)x，∀(x,λ)∈(Sr,+)下它们有相同的Clifford半群分量若(i,x),(x,λ))∈(Lα×Tα)×(Tα×Rα),((j,y),(y,μ))∈(Lβ×Tβ)×(Tβ×Rβ)，则((i,x),(x,λ))+((j,y),(y,μ))=((i,x)+(j,y),(x,λ)+(y,μ))∈(Lα+β×Tα+β)×(Tα+β×Rα+β)，其中(i,x)+(j,y)表示(i,x)与(j,y)在(Sl,+)中的和，(x,λ)+(y,μ)表示(x,λ)与(y,μ)在(Sr,+)中的和.

下面讨论((i,x),(x,λ))∈(Lα×Tα)×(Tα×Rα)与((j,y),(y,μ))∈(Lβ×Tβ)×(Tβ×Rβ)的积.令((i,x),(x,λ))((j,y),(y,μ))=((k,z),(z,c))，下证k(z、c)的选择只依赖于i与j(x与y、λ与μ)的选择.

∀((i,x),(x,λ))∈(Lα×Tα)×(Tα×Rα)，∀((i',x),(x,λ))∈(Lα×Tα)×(Tα×Rα)，((j,y),(y,μ))∈(Lβ×Tβ)×(Tβ×Rβ)，若((i,x),(x,λ))((j,y),(y,μ))=((k,z),(z,c)),((i',x),(x,λ))((j,y),(y,μ))=((k',z'),(z',c'))，则由S满足乘法分配律及E+(S)是(S,·)上的理想可知

((k,z),(z,c))=((i,x),(x,λ))((j,y),(y,μ))

=[((i,0),(0,λ))+((i',x),(x,λ))]((j,y),(y,μ))

=((i,0),(0,λ))((j,y),(y,μ))+((i',x),(x,λ))((j,y),(y,μ))

=((k,0),(0,c))+((k',z'),(z',c'))

=((k,z'),(z',c')),

所以z=z'，c=c'，从而可得z、c的选择与i无关，同理可证z、c的选择与j无关.

同理，∀((i,x),(x,λ))∈(Lα×Tα)×(Tα×Rα)， ∀((i,x),(x,λ'))∈(Lα×Tα)×(Tα×Rα)，((j,y),(y,μ))∈(Lβ×Tβ)×(Tβ×Rβ)，若((i,x),(x,λ))((j,y),(y,μ))=((k,z),(z,c))，((i,x),(x,λ'))((j,y),(y,μ))=((k',z'),(z',c'))，则由S满足乘法分配律及E+(S)是(S,·)上的理想可知

((k,z),(z,c))=((i,x),(x,λ))((j,y),(y,μ))

=[((i,x),(x,λ'))+((i,0),(0,λ))]((j,y),(y,μ))

=((i,x),(x,λ'))((j,y),(y,μ))+((i,0),(0,λ))((j,y),(y,μ))

=((k',z'),(z',c'))+((k,0),(0,c))

=((k',z'),(z',c)),

所以k=k'，z=z'，从而可得k、z的选择与λ无关，同理可证k、z的选择与μ无关.由此可得k(z、c)的选择只依赖于i与j(x与y、λ与μ)的选择.由上面的事实，可以在Sl(Sr)上定义乘法运算如下：

∀(i,x)∈Lα×Tα,(j,y)∈Lβ×Tβ(∀(x,λ)∈Tα×Rα,(y,μ)∈Tβ×Rβ)，

(i,x)(j,y)=(k,z)⟺((i,x),(x,λ))((j,y),(y,μ))=((k,z),(z,λμ))；

(x,λ)(y,μ)=(z,c)⟺((i,x),(x,λ))((j,y),(y,μ))=((ij,z),(z,c)).