基于聚类及霍夫变换的轮对廓形提取算法研究
2020-06-30王洪峥从光涛邢宗义
王洪峥,从光涛,邢宗义,张 永
(1.广州地铁集团有限公司 运营事业总部,广州 510335;2. 南京理工大学 自动化学院,南京 210094)
轮对作为城轨车辆走行部的关键部件,其生产精度及安装精度直接影响车辆运行中乘客的安全及舒适性[1]。目前,广州镇龙14/21 号线快慢车模式已开始运行,快车模式下最高速度可达120 km/h[2]。为保障列车运行安全,对列车轮对尺寸在线检测系统与检测算法都提出了更高的要求。
轮对在线检测系统中,轮对廓形提取是检测算法的重要组成部分,有学者提出小波函数[3]、最优双圆弧拟合[4]等方法实现廓形提取,但这些算法较为复杂;另有学者提出的基于多传感器融合的方法[5],但未考虑噪声影响,会导致廓形在干扰情况下畸变。
本文提出一种结合密度聚类与霍夫变换的轮对廓形提取算法:(1)采用DBSCAN(Density-based Spatial Clustering of Applications with Noise)算法[6]对数据进行聚类处理;(2)采用霍夫变换确定廓形有效区域,并进一步利用曲率熵和多项式拟合来寻找廓形基准点;(3)通过坐标变换与平移,获取完整的轮对廓形。
1 轮对廓形数据采集与聚类
1.1 轮对廓形原始数据采集
当列车驶入在线检测系统的有效工作区域时如图1 所示,激光位移传感器扫描轮对踏面,获取行进中轮对的踏面数据,并经处理后得到轮缘及轮径等轮对尺寸参数值。
在图1 中,位于轨道两侧的传感器3 和传感器4 采集的原始廓形数据,经本文提出的算法处理后,实现轮对廓形提取。
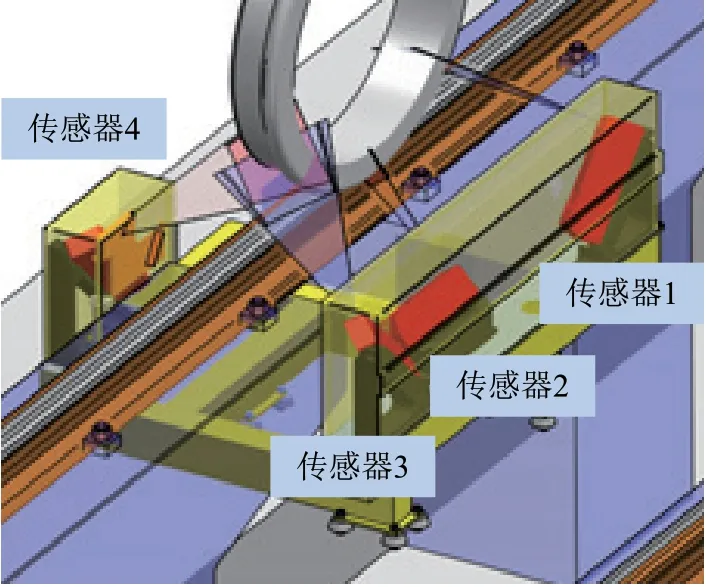
图1 传感器布局示意
在轮对尺寸检测过程中,由于传感器激光投射角度及位置的变化,传感器梯形检测场不仅会扫描到轮对廓形,同时也会采集到轨道以及车底其它部件廓形,且上述廓形会随着车辆运动而发生变化。通过对已安装的在线检测系统的数据分析,可以将采集到的廓形分为6 种:正常廓形、踏面和端面遮挡廓形、踏面遮挡廓形、踏面丢失廓形、端面遮挡廓形和端面丢失廓形,如图2 所示。从图2 可知,除正常廓形数据外,均存在个别噪声点。
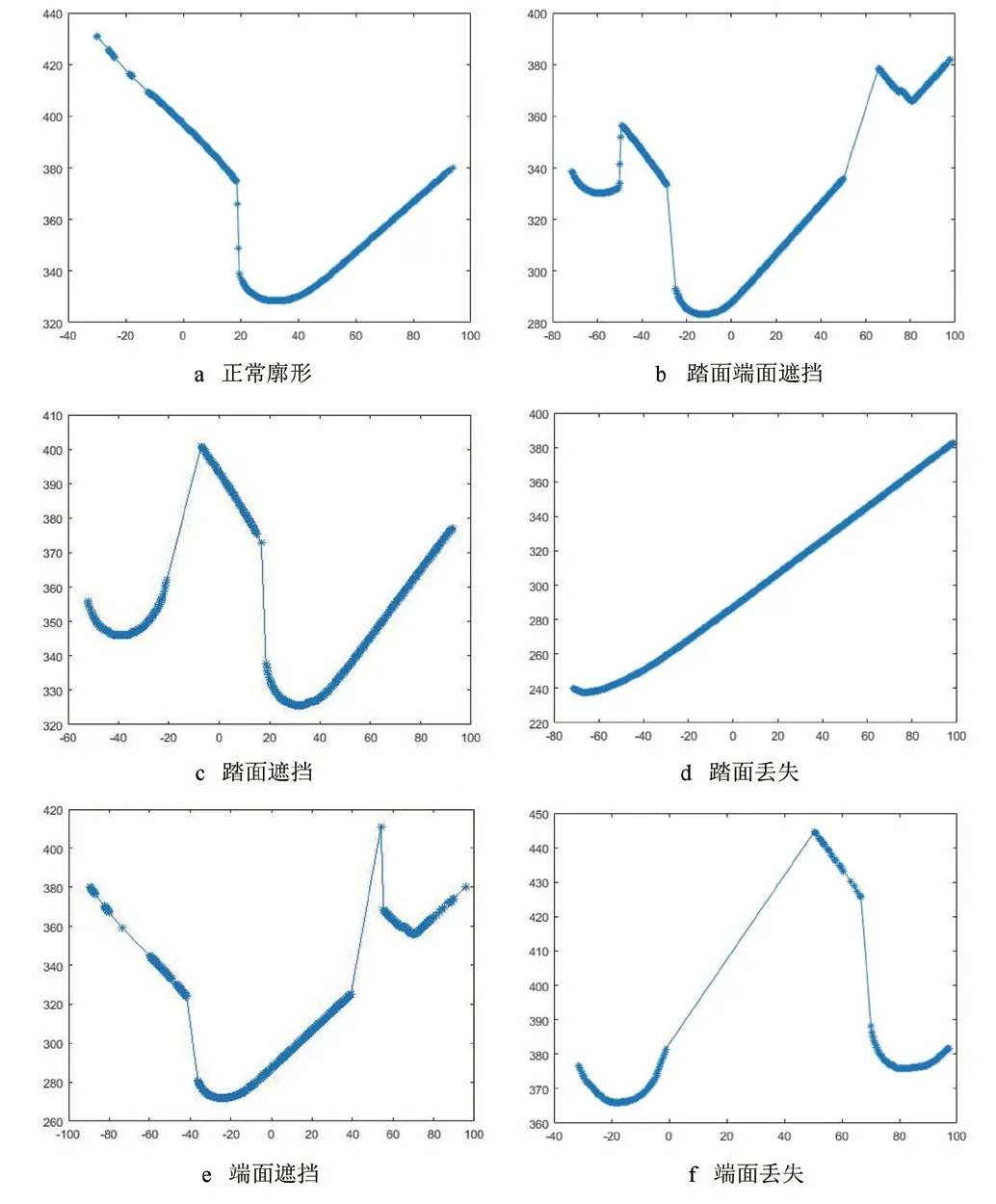
图2 不同轮对廓形示意图
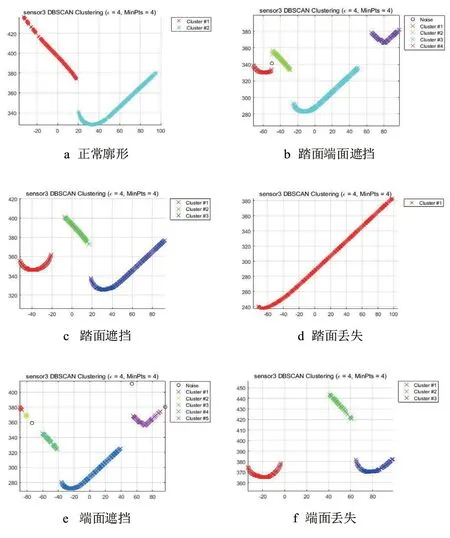
图3 不同轮对廓形的聚类
1.2 轮对廓形数据密度聚类
DBSCAN 算法是一种典型的密度聚类算法,与传统的基于划分和基于层次聚类方法不同,能在含有噪点的数据空间中自动寻找达到密度要求的最大集合,将这些区域识别为一个簇,从而实现含噪声数据中自动发现任意形状族的功能[6],尤其适合于本文中轮对廓形的数据处理。
轮对与其它转向架等部件之间的距离形成的数据密度断层可以使DBSCAN 实现有效聚类。对图2中的轮对廓形数据进行聚类,依据K-Distance 指导原则[7]选取聚类半径及最小聚类点数为4,得到的聚类结果如图3 所示。
从图3 可以看出,DBSCAN 算法可以将连续的轮对踏面或者端面聚合在一类数据中,并形成清晰的边界;如图3a 正常廓形被聚类为2 簇数据,图3e端面遮挡被聚类为5 簇数据,图3d 踏面丢失时仅1簇数据;同时可以看出,DBSCAN 算法能够自动识别噪声点,如图3e 中识别出3 个明显噪声点。由此可见,针对轮对不同的轮对廓形,DBSCAN 算法均能够获得很好的聚类效果。
2 轮对廓形有效区域检测
完成轮对廓形密度聚类后,利用改进霍夫变换进行不同类型廓形判断,并根据廓形种类和有效端面/踏面数据族边界,确定廓形有效区域。
2.1 改进的霍夫变换
为了避免直角斜截霍夫变换时,无法克服斜率较大时的表示问题[8],以及标准霍夫变换需要计算三角函数,计算效率较低的问题,本文将标准霍夫变换检测范围从[0o,180o]变为[-45o,135o],并对新的直线检测范围进行划分,检测范围变为[-45o,45o]和[45o,135o],如图4 所示,两段检测区间的变换公式为:
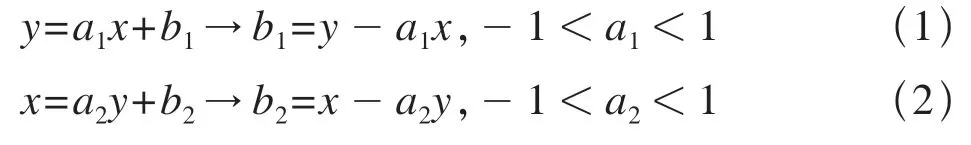
通过上述改进,将原空间中与y轴平行的直线变换到式(2)所对应的直角斜截空间中,消除了单斜截空间的表示问题,因而无需进行三角函数计算。
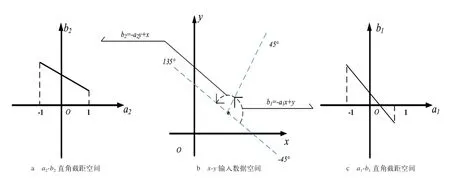
图4 改进霍夫变换示意
2.2 基于改进霍夫变换的轮对廓形区域检测
将DBSCAN 聚类后得到的数据簇,按照簇顺序进行端面和踏面的检测。针对图3 中不同廓形的单个数据族,其包含的有效直线数量不大于2,且端面直线和踏面直线的角度恰好分布在[-45o, 45o]和[45o,135o]两个区间,实现了两个参数空间的对应。因此,在统计霍夫变换参数空间累加变量时,仅需要统计两个参数空间的最大累加值,作为最终检测结果。
在进行端面检测时,将所有聚类后的数据族均进行改进霍夫变换,判断得到的当前数据簇内是否含有直线(即踏面直线或端面直线),然后针对每个廓形统计检测到直线的数据族数量,进行不同类型廓形判断:
(1)若端面直线数量为0,踏面直线数量为1,则为端面丢失;
(2)若端面直线数量为1,踏面直线数量为0,则为踏面丢失;
(3)若端面直线数量为1,踏面直线数量为1,则为廓形正常;
(4)若端面直线数量为>1,踏面直线数量为1,则为端面遮挡;
(5)若端面直线数量为1,踏面直线数量为>1,则为踏面遮挡;
(6)若端面直线数量>1,踏面直线数量为>1,则为端面和踏面遮挡;否则无有效目标。
针对不同的廓形类型,需要将其有效数据族作为边界,实现廓形有效区域检测,具体描述如下:
(1)对于正常端面,提取当前端面直线及踏面直线所在数据簇编号为边界,提取此边界内所有数据簇;
(2)对于端面遮挡,当端面直线检测数量大于1 时,取点数最大端面作为有效端面,而后同正常端面一样处理;
(3)对于踏面遮挡,当踏面直线检测数量大于1 时,取该踏面距离端面数据簇最近的数据簇为有效踏面,而后同正常端面一样处理;
(4)对于端面和踏面遮挡,当端面直线检测数量大于1 时,取点数最大端面作为有效端面,而后同踏面遮挡一样处理;
(5)端面丢失,因无法进行下一步计算,直接作为无效数据处理;
(6)踏面丢失,此类型数据仍然可以用于后续计算轮径值,取端面所在簇数据为有效数据簇。
轮对廓形聚类与有效区域检测的流程如图5 所示,依据该流程对图4 中不同廓形进行有效区域检测,结果如图6 所示。
从图6 可知,图6a 为正常廓形,图6b、6c 和6e 均在红框中检测出含有踏面端面及轮缘的轮对有效廓形,这4 种廓形有效数据点数分别为348、321、324、301,图6d 有效区域内数据点数为563;图6f为端面丢失,由于失去计算意义,因此无有效检测结果。由此可见,改进的霍夫变换能够实现6 种轮对廓形的有效区域检测。
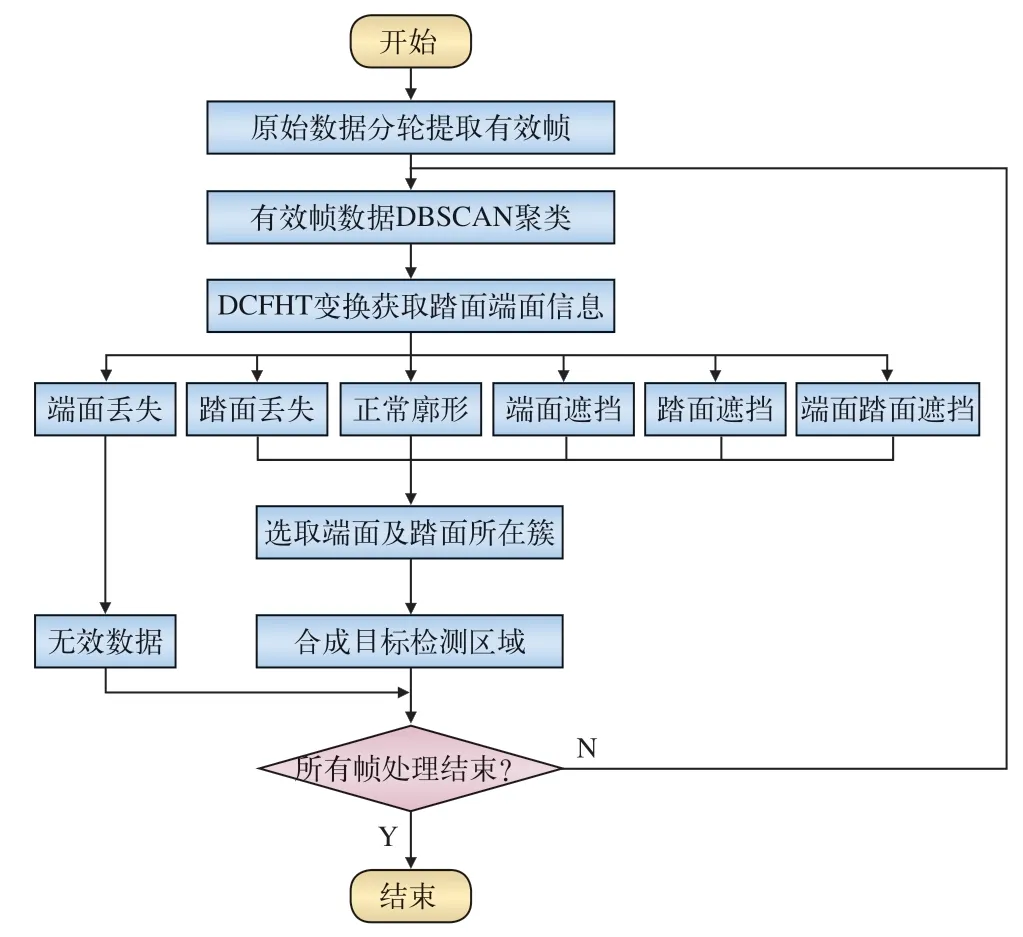
图5 轮对廓形有效区域检测流程

图6 轮对廓形有效区域检测结果
3 轮对廓形匹配
完成轮对廓形有效区域检测后,对得到的廓形进行坐标旋转、轮缘曲线拟合和基准点对准等廓形匹配操作,完成完整的轮对廓形提取。
3.1 坐标旋转
由于轮对尺寸在线检测系统各传感器存在偏转角如图7 所示,以传感器3 和传感器4 为例,对其廓形进行如下坐标旋转[9]。
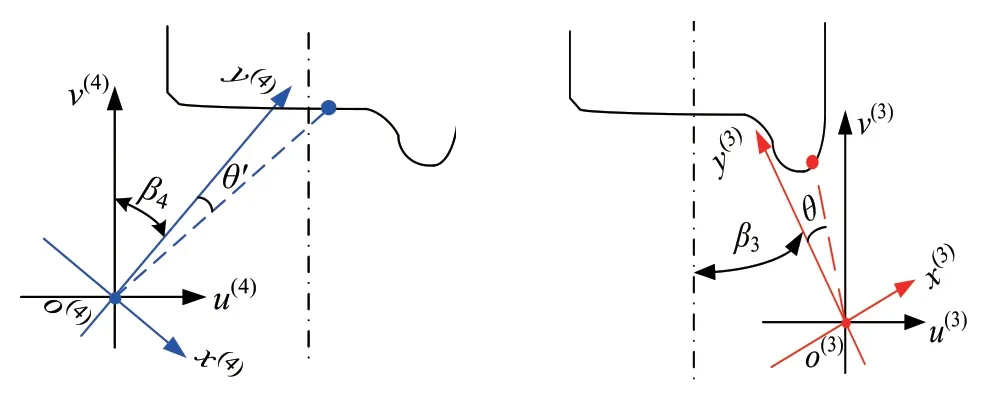
图7 坐标旋转变换过程
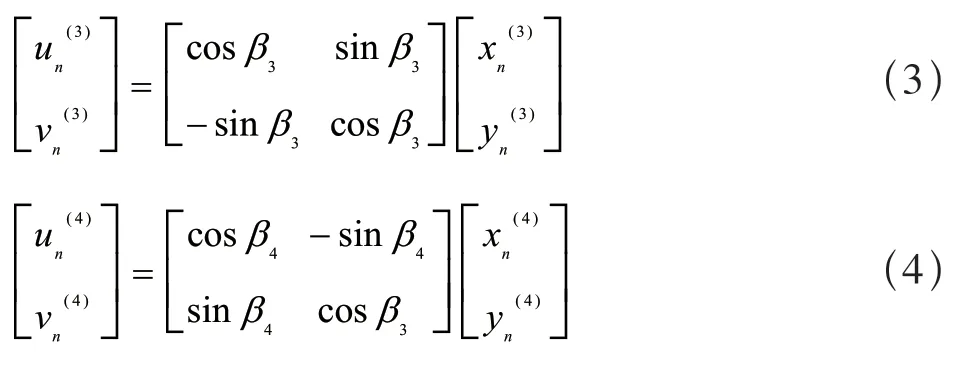
式(3)、式(4)中,角度β3、β4为传感器安装设计偏转角为目标区域廓形点在传感器3 和传感器4 自有坐标系上的坐标。坐标变换前轮对廓形如图8 所示,坐标变换结果如图9 所示,可见传感器廓形的端面坐标旋转后与水平轴基本垂直。

图8 传感器3和传感器4坐标旋转前轮对廓形
3.2 基于曲率熵的曲线拟合
轮对廓形由一组离散数据构成,在后续基准点计算时,需要对基准点附近区域进行轮廓线的曲线拟合。根据轮对廓形的曲率变化,对廓形进行分段曲线拟合。廓形曲率定义为:

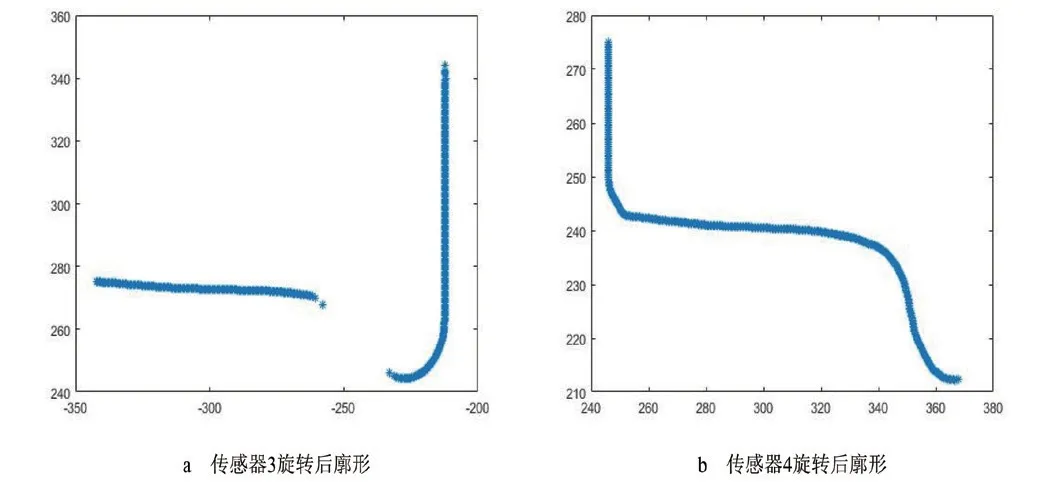
图9 传感器3和传感器4坐标旋转后轮对廓形
其中,vi′为第i个离散数据点的一阶导数;vi"为第i个离散数据点的二阶导数。
以传感器3 数据为例进行说明,其廓形图及其曲率图如图10 所示;由图10b 可见,最大曲率值接近1.2,位于横坐标[-236.9 -223] 之间,对应于图10(a)的纵坐标最低点,即轮对轮缘最低点,符合现场经验认知。
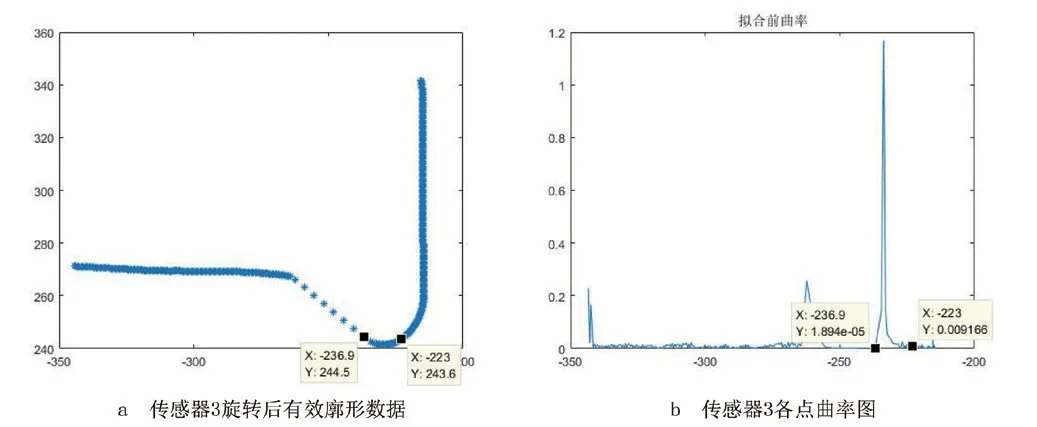
图10 廓形图及其曲率图
为确定最大曲率前后坐标的合理范围,引入曲率熵[10-11],对某段区间内曲率信号的概率分布进行评估,其定义为:

其中,Q为区间(ε,ε+l)的曲率概率分布,ε为当前滑动区间起点,l为当前滑动区间长度。
以传感器3 数据为例进行说明,针对不同的区间起点和区间长度,计算廓形数据的曲率熵,其结果如图11 所示;曲率熵最大值为2.779,对应的滑动区间起点为264,区间长度为19。由此可见,能够很容易确定最大曲率前后坐标的合理范围,即轮对实际的待拟合轮缘范围。
在曲率熵最大点前后合理范围内采用最小二乘法多项式进行曲线拟合[12],可以获取轮缘最低点纵坐标,作为轮缘基准点用于后续轮对几何参数计算。
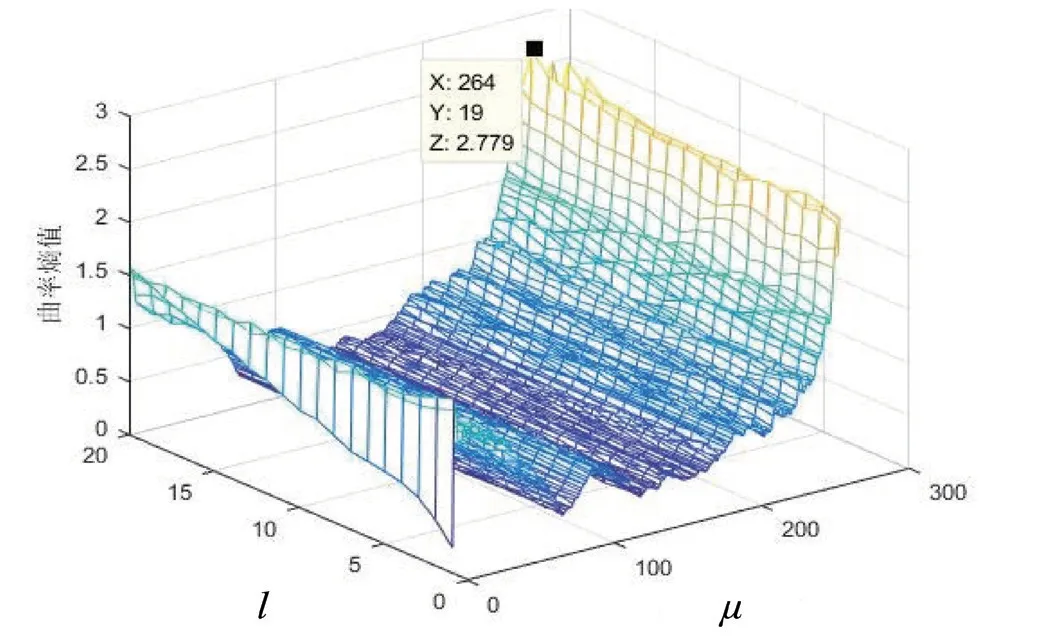
图11 廓形图曲率熵
多项式拟合目标为:
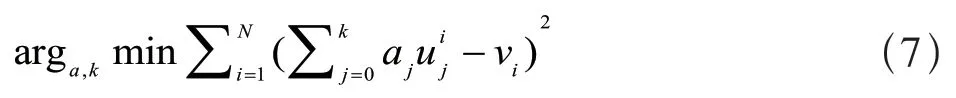
其中,k为多项式阶数,N为数据点个数,a为多项式系数,uj与vi为拟合点坐标值。
针对传感器3 和传感器4 的轮缘最低点,对其区间进行多项式拟合:

其中,a为传感器3 的多项式系数,b为传感器4 的多项式系数,采用4 阶多项式拟合。
3.3 基于踏面基准点的廓形匹配
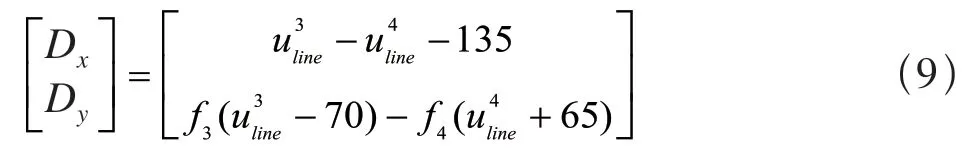
经过平移匹配后,可将由传感器3 和传感器4生成的廓形匹配为完整的轮对轮廓线,如图12 所示,从而可以根据轮对几何参数定义,进一步计算轮对尺寸参数[13]。
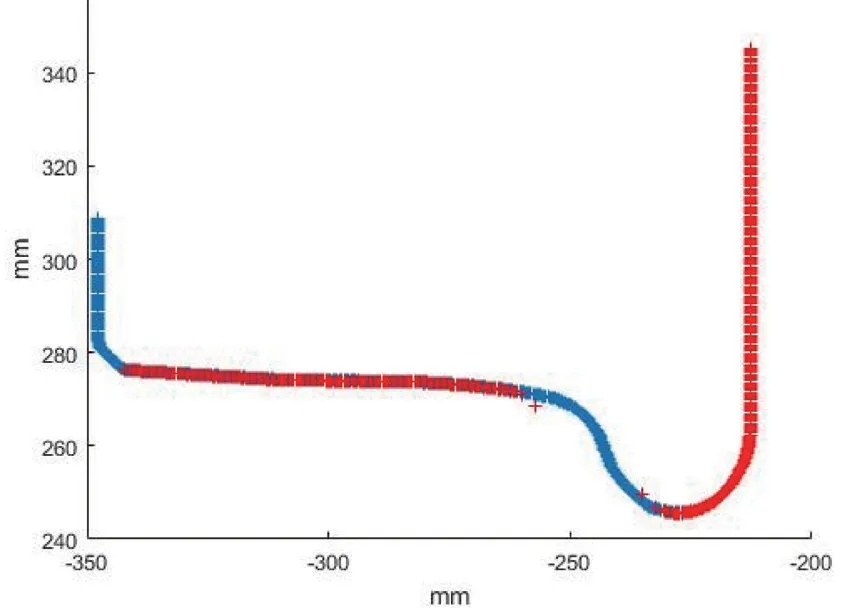
图12 传感器3及传感器4目标廓形匹配
4 试验结果及分析
本文算法程序采用C++语言编写,运行于广州地铁14 号线镇龙车辆段轮对检测试验棚服务器内。选取14 号线上试验用车辆(编号为14019020)反复通过轮对检测棚,由安装于轨道下方的传感器读取原始数据,轨旁控制机柜读取传感器采集的数据后,通过TCP/IP 协议将其传输至运行该算法程序的服务器;服务器对数据进行目标廓形提取,并计算轮缘参数,共进行7 次重复试验。取该车辆两节车厢共8个轮对,以轮缘高度为例进行精度分析,以验证本文算法的有效性。
轮缘高度检测结果见表1,其标准差如图13 所示,标准差均小于0.15,且优于人工检测值的标准差,可见系统检测重复性好。
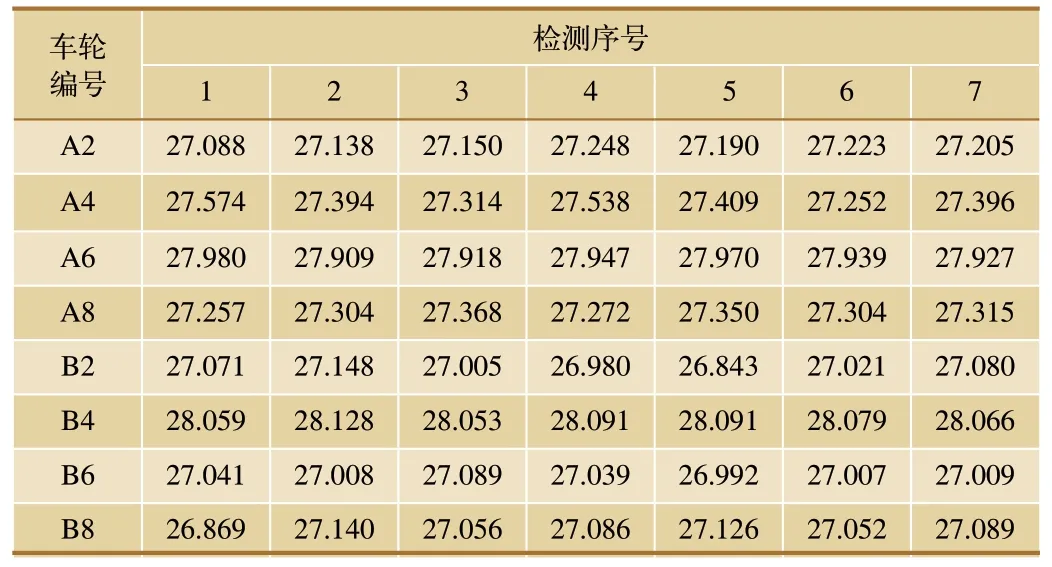
表1 轮缘高度7次检测结果
图14 给出了系统检测与人工检测最大最小值的比较,可见系统检测的最值区域完全包含在人工检测最值区域内,说明系统测量精度优于人工测量。
5 结束语
本文提出一种轮对廓形提取算法,可用于轮对尺寸参数计算。采用密度聚类DBSCAN 及改进霍夫变换实现对传感器各种廓形有效区域提取,根据目标廓形曲率熵的变化特点,对轮缘廓形进行曲线拟合;最后,对其进行基于踏面基准点的廓形匹配,实现旋转及平移矩阵的在线计算,得到完整的轮对廓形。通过现场试验,验证了该算法在轮缘高度参数计算中的精度及可靠性,能够满足轮对几何参数计算的需求。
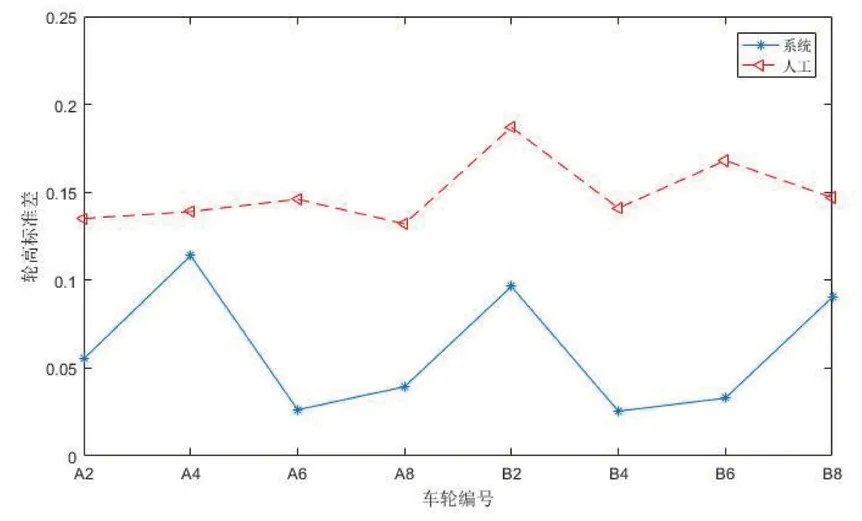
图13 轮缘高度7次测量标准差
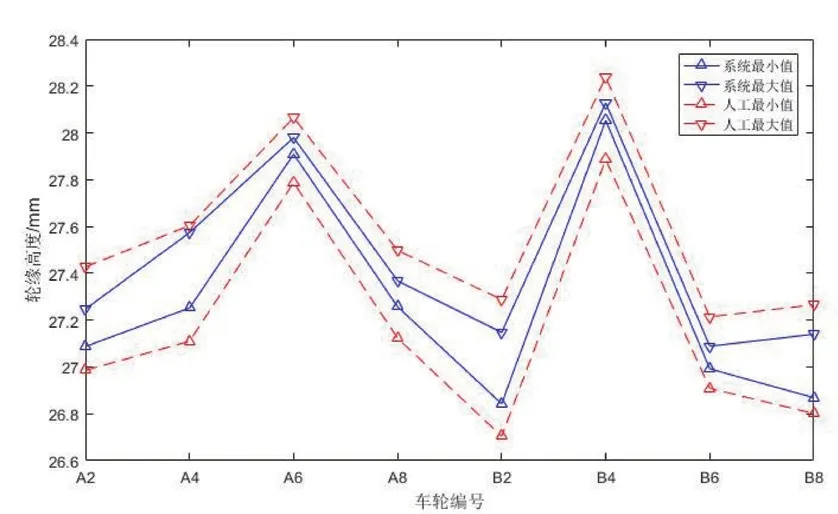
图14 轮缘高度最值与人工最值比较
