基于参数优化VMD和SPWVD的轨道波磨辨识方法

张海强，王 楠，刘 松，李柄奎

（1.广州地铁集团有限公司 运营事业总部，广州 510335；2. 南京理工大学 自动化学院，南京 210094；3.中国移动江苏公司 扬州分公司，扬州 225000）

随着城市轨道交通技术的快速发展，地铁运行速度逐步提升，钢轨表面受到的冲击愈加严重，导致轨道表面容易产生波磨磨耗。当车辆行驶至波磨路段时，会引起强烈的震动和冲击，导致列车部件受损和乘客舒适度下降，严重时可能会发生列车脱轨事故。弦测法[1-2]和惯性基准法[3-4]是目前轨道波磨检测的主要方法，得到了深入研究。孙锐等人[5]以实测轨道波磨数据为基础采用ABAQUS 仿真软件，建立了轮轨关系有限元模型，研究了不同参数对车辆驶过波磨时的动态影响，并论证了不同波磨之间存在共生关系。张厚贵等人[6]通过大量的试验和现场调研，对波磨形成机理进行了探讨，结果表明，当钢轨模态频率因轨下结构与轮对反共振频率一致时，轮轨系统将发生强烈振动，引起轨面磨耗损伤，在反馈- 循环机制下，会生成与轨下模态频率相对应的某种波长的波磨。Oyarzabal 等人[7]应用钢轨波磨萌生和扩展（RACING）对轨道支撑结构中14 个最为明显的因素进行优化，以实现波磨产生概率的最小化。Valehrach J 等人[8]对轨道波磨的产生环境进行分析，发现列车行驶速度是影响波磨发展的因素之一。Kurzeck 等人[9]对小半径曲线轨道的波磨进行分析，验证了轮轨间的摩擦振动对轨道波磨的产生具有很大的相关性，并且讨论了轮轨之间的摩擦自激振动需要的条件。Zhai 等人[10]利用SIMPACK 软件进行转向架加速度数据仿真，利用连续小波分析得到的特征频率和经验模态分解得到的特征模态可以对轨道波磨进行诊断识别。黄文等人[11]研究了小波包能量熵方法，通过对波磨仿真数据的处理，能够获得轨道波磨位置与波长，并通过现场数据验证了检测方法的可行性。王乃珍等人[12]通过建立灰色区间预测模型对轨道的不平顺状态进行预测，并基于京九线的实测数据进行验证。

本文提出了一种基于参数优化变分模态分解（VMD，Variational Mode Decomposition）和平滑伪维格纳分布（SPWVD ，Smooth Pseudo Wigner-Ville Distribution）的轨道波磨辨识方法，对列车轴箱垂向振动加速度信号进行处理分析，以分解信号的包络熵为特征量，设定故障阈值，识别轨道波磨故障，计算波磨波长并确定轨道波磨发生的位置。本方法不仅消除了VMD 分解参数选取不确定的弊端，而且克服了振动信号时频分解过程中出现的模态混叠问题，具有良好的准确性，可辅助轨道波磨辨识，提高轨道维保效率。

1 基本理论

1.1 变步长最小均方算法

变步长最小均方（VSSLMS，VariableStep Size Least Mean Square）算法[13-14]具有计算量小、自适应能力高等优点，且其收敛速度在算法不同时期可以采用不同步长来控制，因此在信号处理的各个领域得到了广泛的应用。

令d(n)表示期望输出信号，W(n)表示滤波器的抽头权向量，e(n)表示误差信号，X(n)表示输入信号向量，则它们有如下关系：

式中，μ(n)为步长参数，并且步长迭代关系为：

式中，μmax是获得最大可能收敛速率的步长；μmin是具有跟踪能力的最小步长；α＞0，β＜1，α为步长遗传因子，主要作用是确定算法收敛时的步长值，β决定步长受误差瞬时能量的影响程度，决定着算法的开始和跟踪速度。

在VSSLMS 的初期阶段，e(n)很大，且指数an衰减很小，因此相对的步长μ(n)比较大，算法收敛比较快。在VSSLMS 的收敛末期，e(n)较小，而指数an衰减较大，所以对应的步长μ(n)较小。由于VSSLMS 能较好地达到稳态误差和收敛速率之间的平衡，且容易实现，因此本文用该方法对振动信号进行滤波，取得了较好的效果。

1.2 参数优化VMD

1.2.1 VMD

Dragomiretskiy 等人[15]提出了VMD 方法，属于一类非递归分解方法，自适应同步提取复杂信号中的调幅-调频分量[16]。变分模式分解将信号x(t)分解为一组本征模态分量（IMF）ck(t)，通过这些本征模态分量，可以重构信号，在频域内迭代更新各个本征模态分量ck(t)，将本征模态分量频谱的重心作为中心频率ωk。

假设本征模态分量ck(t)在频域内紧致聚集在中心频率ωk周围，即具有稀疏性质。每个本征模态分量的稀疏性质通过它的带宽来描述：（1）应用Hibert变换构造其解析信号，以便获得非负频率的单边频谱；（2）通过和频率调整至各自中心频率处的指数谐波相乘，将频谱平移至基带；（3）通过梯度的平方l2范数估计带宽。

为了将约束变分优化问题转化为无约束形式，增加惩罚项和Lagrance 乘子，以便快速收敛并增强约束，所以，将最小化的目标函数转换为增广Lagrance 函数：

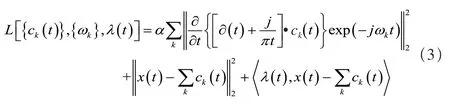
式中，λ(t)为Lagrance 乘子，α 为数据真实性约束的平衡参数表示内积。

求解与式（3）等价的最小化问题，应用最优解更新每个本征模态分量ck(t)：

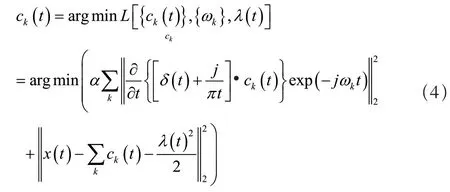
将式（4）频域内的解取Fourier 逆变换并取实部，获得时域里的本征模态分量。

求解和式（3）等价的最小化问题，应用最优解更新每个本征模态分量ck(t)的中心频率ωk：

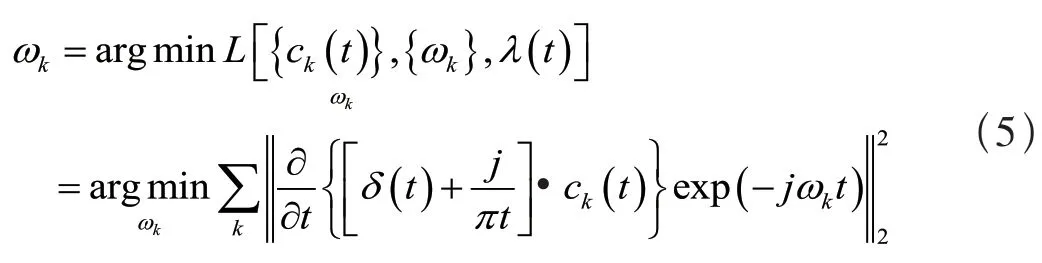
变分模式分解的完整算法如下。

（2）对于k=1，2，…，K 及所有ω(ω ≥0)，更新每个本征模态分量ck(t)及其中心频率ωk；

（3）对于所有ω ≥0，更新Lagrance 乘子；

（4）检查收敛条件：

1.2.2 VMD参数优化

虽然变分模态分解具有非递归同步分解本质，从而有效避免了递归分解算法的缺点，如对噪声的采样敏感性，以及在极值插值过程中产生的上下包络过拟合和欠拟合等问题，但是对振动信号分解结果影响比较大的参数分解模态数K 与惩罚参数α 却不能自适应选取，这很容易对分解结果造成较大影响。因此，提出了一种基于变分模态分解信号中IMF 分量最大峭度值参数优化选择方法。参数优化VMD 算法的流程如图1 所示，详细步骤如下：

（1）设定参数α 的搜索区间为[200 3 000]，搜索步长为10，参数K 的搜索区间设为[2 10]，搜索步长为1，在（K，α）的坐标平面上构建了一个二维网格；

（2）选取（K，α）平面网格点上的参数值，对原始信号实施变分模态分解；

（3）求出分解后的原始信号各IMF 分量中最大峭度值并保存；

（4）遍历网格中所有的点，并完成步骤（2）、步骤（3）；

（5）从保存的峭度值中筛选出最大的，这个最大峭度值所采用的参数K 值与α 值即为最优。

图1 参数优化VMD算法流程

1.3 SPWVD

维格纳分布（WVD，Wigner-Ville-Distribution）是非平稳信号分析中常见的二次型时频分布，广泛应用在各种领域[17]，但WVD 可能会产生交叉项，从而输出虚假分量。因此，为避免信号分析时的交叉项干扰，获得良好的信号时频分析效果，本文采用时域加窗的WVD 对信号的WVD 在时域和频域做平滑处理的方法进行时频分析[18]。

根据WVD 的特性，两个时域信号乘积的WVD与各自WVD 在频域的卷积相等，因此可以表示成：

根据上式能够得知，在时域加窗之后的结果与在频域进行低通平滑滤波效果等同。如果再在频域加一个窗函数，等同于在时域做卷积。两个时域信号卷积后的WVD 等于各自WVD 在时间轴上的卷积，相当于对WVD 变换在时域做平滑。经过时域与频域加窗处理后的WVD 称为平滑伪维格纳分布（SPWVD）。

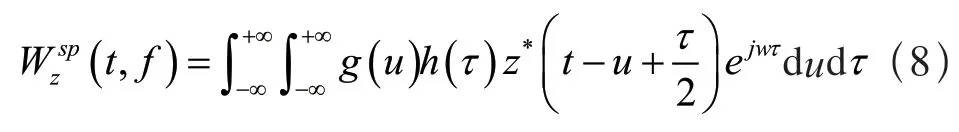
式中，h(t)和g(t)是奇数长度的窗函数，满足h(0)=1 和G(0)=1，G(f)为g(t)的傅里叶变换。

2 算法流程

本文提出的基于参数优化VMD 和SPWVD 的波磨辨识算法如图2 所示，步骤描述如下：

图2 轨道波磨辨识算法流程

（1）采集轴箱垂向振动信号，进行去除干扰及噪声等滤波处理；

（2）将滤波后的振动信号进行参数优化的变分模态分解；

（3）选取信号的本征模态分量，计算波磨的特征值包络谱熵；

（4）根据阈值判断是否存在波磨；

（5）若采集的垂向振动信号，存在波磨，则对分解后的振动信号进行SPWVD 时频分析，确定波磨中心频率及波磨位置，计算波磨波长。

3 仿真分析

3.1 波磨仿真

轨道波磨能够用一个近似余弦的信号来描述，为了更好地对轨道波磨进行仿真，本文进行4 种不同的波磨仿真实验。钢轨长度为40 m，采样频率为1 kHz，车速为10 m/s，一侧轨道添加美国五级轨道垂向不平顺（AAR5），另一侧轨道在特定位置添加不同波磨，详细的参数设置如表1 所示。

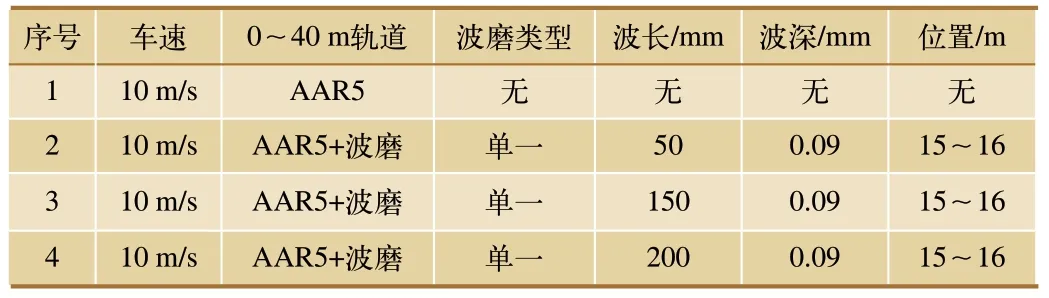
表1 轨道波磨参数设置

按照表1 所述参数，将轨道不平顺数据制作成tre 格式的文件，导入SIMPACK 多体动力学软件，并建立相应的轨道激励函数，添加至列车仿真模型，然后分别完成速度、采集频率、时间等一系列参数设置后，进行离线分析，保存轴箱振动的仿真结果数据，得到振动信号时域图如图3、图4 所示，由图可见，当添加的轨道波磨波深相同时，随着波长的增加，轴箱垂向振动信号幅值呈现下降的趋势。

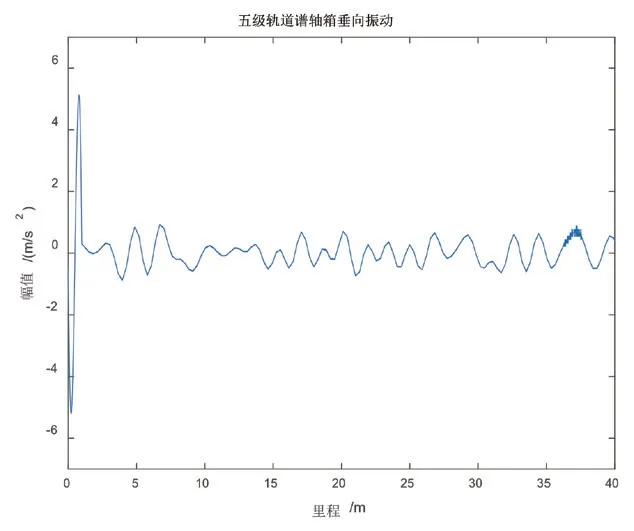
图3 仅添加AAR5的轴箱垂向振动时域

3.2 波磨故障辨识

由于仿真信号的振动数据不含有噪声信号，故不再应用VSSLMS 方法进行滤波，直接采用参数优化VMD 方法进行模态分解，根据轴箱垂向振动信号的模态分解结果，计算分解后信号的包络熵值，K、α参数值及包络熵值，如表2 所示。

图4 不同波长0.09 mm波深轴箱垂向振动时域

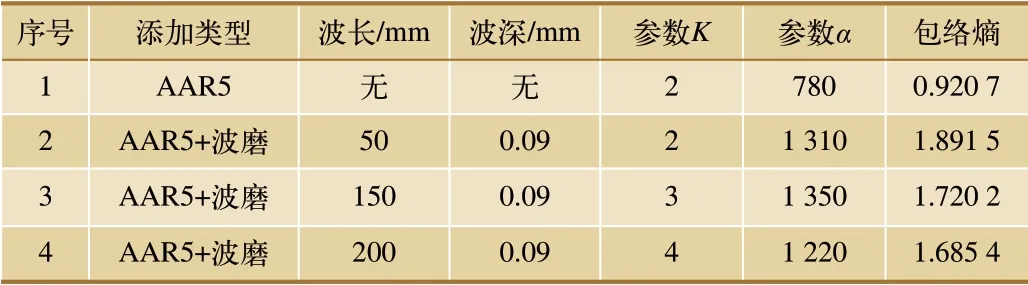
表2 轴箱垂向振动参数优化VMD的分解参数及信号包络熵

由表2 中结果可知，仅含美国五级轨道谱的第一组包络熵值为0.920 7，而其他添加轨道不平顺的包络熵数据远大于第一组的值，因此，包络熵可以作为轨道是否发生波磨的特征值，参考仅含美国五级轨道谱的包络熵值，为留有一定的工程余量设置阈值为0.95，大于阈值判定为存在轨道波磨故障，反之则无轨道波磨故障。接下来为了进一步分析轨道波磨发生的位置及波长范围，本文选取第4 组数据，用SPWVD 方法对分解后的垂向振动信号进行时频分析，分析结果如图5 所示。

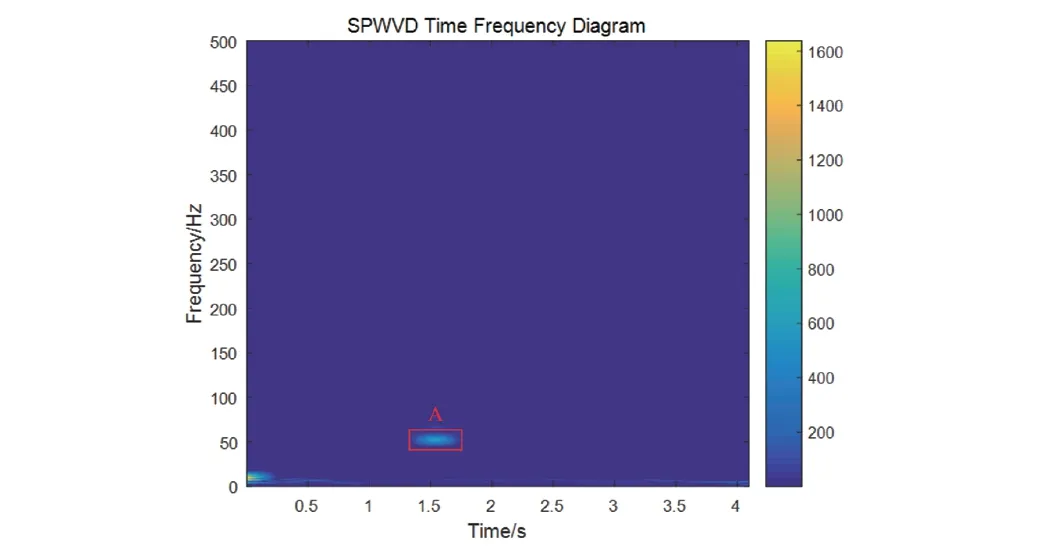
图5 200 mm波长0.09 mm波深时频

由图5 可知，在A 处1.41 s ～1.69 s 时发生频率集中，频率范围为[44.91 Hz 56.63 Hz]。时频图中零点起始位置也有频率集中现象，但经过分析可知，此位置是由美国五级轨道谱所引起，并非添加轨道波磨所致。由于采样频率设置为1 kHz，根据波磨波长λ与振动频率f的关系式可知：

式中，v为列车速度。

为了准确计算波磨波长，f取频率集中区的中心频率，计算可知，图5 中添加轨道波磨的位置在14.1 m ～16.9 m，这与在15 m ～16 m 处的添加波磨位置基本稳合，波长为199.63 mm，与仿真200 mm波磨波长非常接近。

4 实例分析

为了进一步验证波磨故障辨识算法的有效性，本节利用轨道波磨在线检测系统设备，对广州地铁8号线的轨道线路进行检测试验，检测列车运行速度为72 km/h，采样频率是10 kHz。本文截取一段1 km长度包含异常的轴箱垂向振动信号数据进行分析，其振动信号波形如图6 所示。由图6 可知，实测轴箱垂向振动信号中含有大量噪声干扰，因此需要对采集的振动信号进行滤波处理，本文采用VSSLMS方法滤波，滤波后的波形如图7 所示。

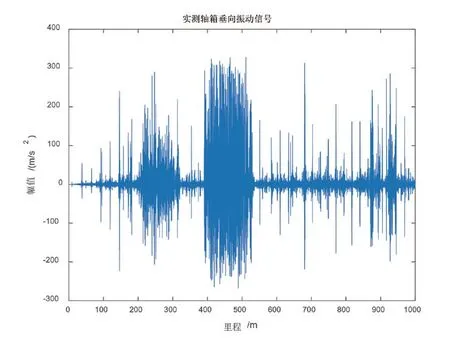
图6 轴箱垂向振动信号波形（实测值）

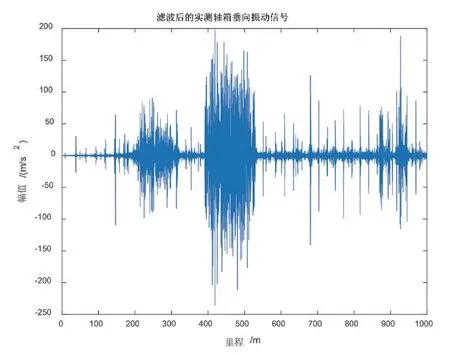
图7 轴箱垂向振动信号波形（滤波后）

由图7 可知，经过滤波后的轴箱振动信号在200 m ～300 m 及390 m ～530 m 处具有比较大的幅值波动，特别是在里程390 m ～530 m 处，不仅波幅大而且里程较长，并且从图7 还可以看到较多的振动信号尖峰，分析可知，这是由于城轨车辆运行到钢轨接头处产生的冲击力变化所致。

为了计算方便，本文截取350 m ～550 m 里程处的滤波振动信号进行数据分析，并且对此段数据5倍降频处理，采样频率降为2 kHz，如图8 所示。

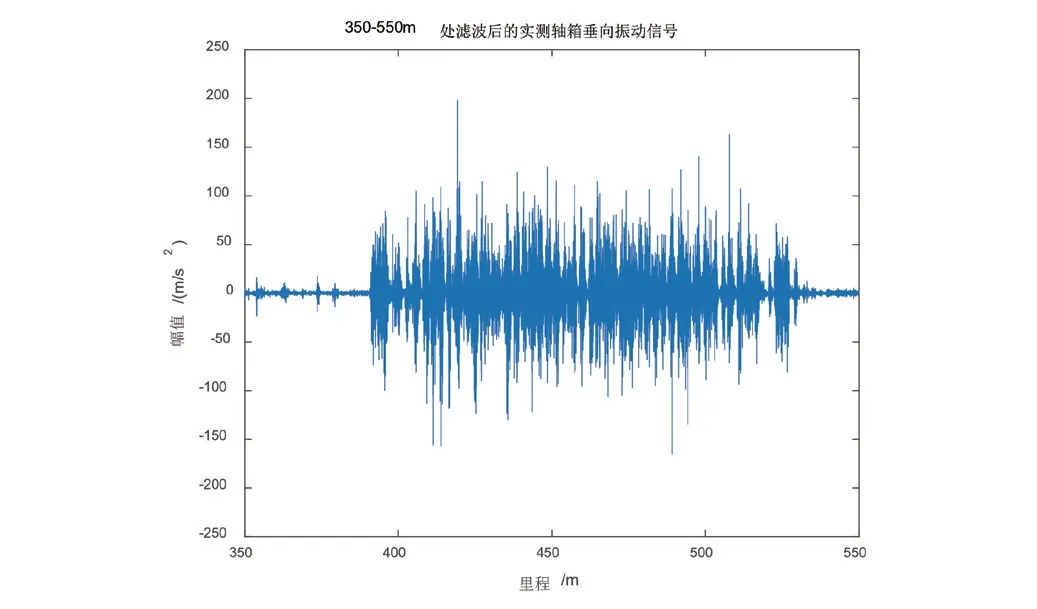
图8 350 m～550 m处滤波后的实测轴箱垂向振动信号

在350 m ～550 m 里程处滤波信号经过参数优化的变分模态分解后，计算各IMF 分量的包络熵为13.936，而这段轨道正常轴向振动的信号的包络熵值为1.917，故可以判断出该段轨道存在波磨。

为了进一步验证检测方法的有效性，在广州地铁工程人员的配合下，对440 m ～480 m 处轨道进行检查，发现该段线路发生了如图9 所示的波磨故障，从图中可以明显看到钢轨表面发生了波浪形的磨耗，测量后得到该处轨道波磨的波长大致在76 mm 左右，与本方法检测结果误差最大仅为3.92%，从而验证了本文所述方法对波磨故障检测的有效性。

图9 现场存在轨道波磨路段

5 结束语

本文通过采集环境激励下列车轴箱上振动加速度传感器的响应信号，利用变步长的LMS 自适应滤波方法对采集的加速度信号过滤作降噪处理，采用参数优化VMD 方法对信号进行分解，以分解信号的包络熵为故障辨识指标，根据正常轨道的包络熵设定阈值，识别轨道波磨，最后利用SPWVD 方法对含有波磨的振动信号进行时频分析。具体结论如下：

（1）参数优化VMD 算法不仅克服了VMD 分解参数不能自适应选取的弊端，并且通过对比振动信号VMD 分解图及各IMF 分量的时频图，充分说明了VMD 分解在关于抑制模态混叠方面的优越性；

（2）根据不同故障振动信号分解时包络谱的差异，提出了以分解信号的包络熵为轨道波磨辨识指标，通过设定故障阈值，识别轨道波磨；

（3）基于SPWVD 方法含轨道波磨振动信号进行时频分析，根据分析结果，可以判断出轨道波磨位置，并且利用波磨波长λ与振动频率f的关系，能够计算出波磨波长。