基于压痕功的加工表面残余应力测试实验

邱 硕，杨文玉，周金强，陈文成，孔维森

（1.上海航天设备制造总厂有限公司，上海 200245；2.华中科技大学 数字制造装备与技术国家重点实验室，湖北 武汉 430074）

0 引言

复杂曲面类零件，如桨叶等，对数控装备制造要求较高，合理的加工工艺参数对优化该类零件的产品质量十分重要。通常在工况下可调距螺旋桨桨叶最不利的晶体在最大剪切应力的作用表面形成滑移区，滑移区域开裂导致微观裂纹，通过汇集生成宏观裂纹［1］。通过对失效桨叶的调查，表面残余应力对桨叶的失效影响显著［2］。在金属切削加工中，切削参数、刀具参数、工件材料等都会对零件表面残余应力的产生造成影响。残余应力是影响表面质量的关键因素，连接工艺参数与疲劳性能的桥梁，是研究材料性能较关键的物理量。因此，如何通过优化工艺参数使残余应力的分布与大小能满足条件，从而实现更长的服役寿命，成为了目前一个热门的研究课题。

残余应力检测技术可分为有损检测和无损检测。微纳米压痕法作为无损检测的新兴方法，比较适合桨叶的在役检测。BOLSHSKOV 等［3］为了解应力对硬度、接触面积、弹性模量的影响，研究了平面等轴残余应力对8009 铝合金压入响应的影响，探索了压痕试验测量等轴残余应力的方法；SWADENER 等［4］在使用球形压头进行压痕实验中，提出了用接触压力代替接触面积来计算残余应力的模型，根据压痕深度与应力的关系，建立残余应力和等效应变的相互关系，进而推算残余应力值；刘琦［5］提出一种基于压痕功的微纳米表层硬度检测方法，通过材料的载荷压深曲线和压痕三维形貌，为分析和研究压痕尺寸效应的成因奠定了基础；谭森［6］对表面存在不同残余应力的低碳钢进行压痕实验有限元仿真，得出载荷位移曲线，然后根据实际压痕深度计算表面平均残余应力；金宏平［7］通过对载荷位移曲线分析，分离出残余应力，建立残余应力对压痕功和等效应变间的关系，提出了基于等效应变的残余应力的能量测量方法。上述研究成果为镍铝青铜材料在加工过程中表面残余应力的检测提供了参考。

1 测试原理

通过压痕技术测量材料表面残余应力一般有两种方法：一种基于断裂力学理论，一种基于残余应力对压痕响应的影响。前者仅仅适用于脆性材料，如陶瓷等；而后者借助有限元模拟技术分析残余应力对材料接触面积、加/卸载曲线的影响，得出相应的函数关系。

压痕试验的理论基础为Hertz 接触理论，压头与试样的接触为非协调接触，两者接触面积相较于试样本身很小，可认为应力仅高度集中在接触附近区域。一个完整的压痕试验可分为两个过程：加载阶段和卸载阶段。典型压痕载荷-位移曲线如图1所示，横坐标h表示压痕深度，纵坐标F表示压头施加的载荷。最终深度hp为压头在试样上留下的永久塑性变形，接触深度hr为卸载初始段斜率延长线与位移轴的交点，由加载曲线和卸载曲线及位移曲线所包围的面积可得到材料变形所吸收的能量，即加载功为

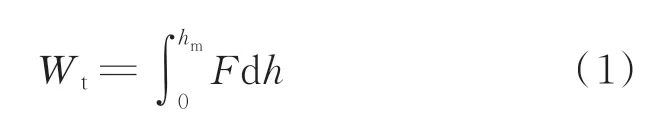
式中：hm为最大压痕深度，且卸载功为

图1 典型压痕载荷-位移曲线Fig.1 Typical curves of indentation load-displacement

任意一点的应力状态可以使用对称矩阵Σij来表示，该矩阵也就是应力张量。根据塑性变形理论，应力张量可分为球张量和应力偏张量：

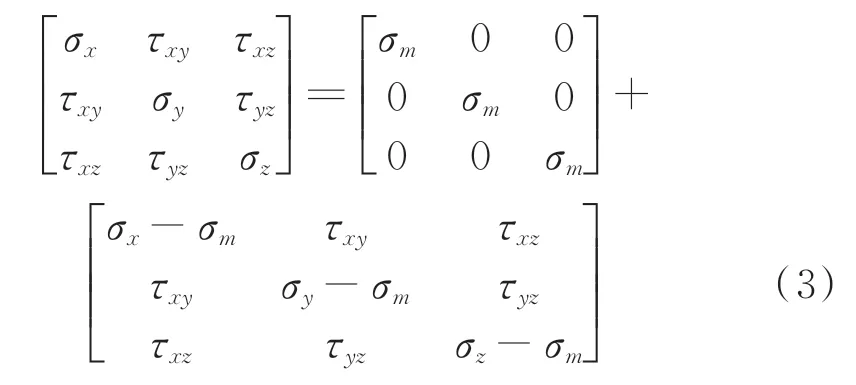
式中：σi为i（i=x，y，z）方向的正应力；τjk（j&k=x，y，z）中j为应力分量作用面，k为应力分量作用方向；σm为平均应力，是不变量，与所取坐标无关。当应力状态确定时，它为单值。

对存在残余应力的材料单元，将残余应力分解成平均残余应力和纯剪切应力：

当压痕深度一定时，在残余拉/压应力和无残余应力状态下的载荷位移曲线，从A到B过程中释放的应力即为球张量，这样材料在压痕状态下塑性变形不变，有

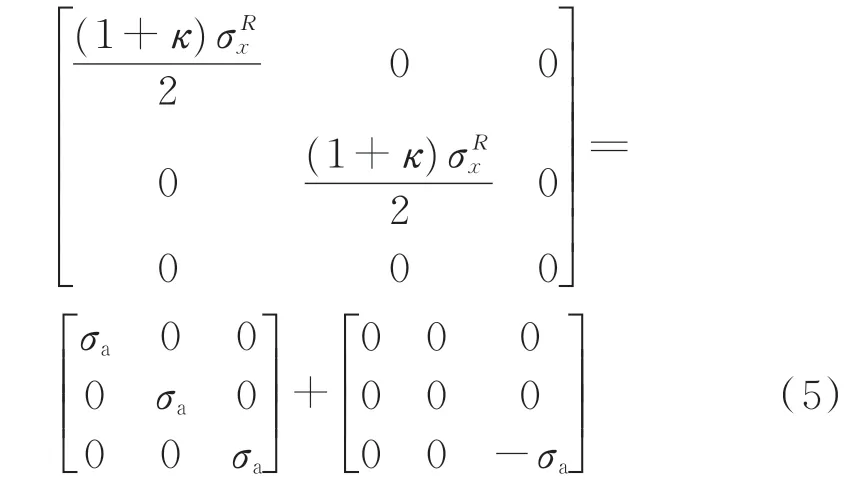
等效于Z方向给材料施加的压力σz=−σa，则该过程中式（5）中的第一项静水压力为0。如图2 所示，假设材料在无应力状态下压入深度为ht时，对应的接触面积为Ac。则有

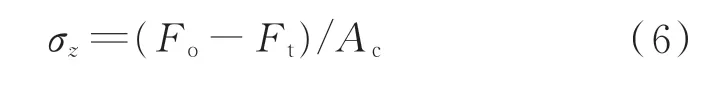
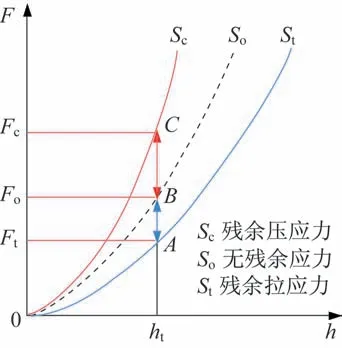
图2 加载曲线随应力状态的变化图Fig.2 Diagram of loading curves with different stress states

材料单元从C到B过程中有

在压痕实验中，采用球形压头，其加载段载荷

式中：E、ν分别为被检测试样的弹性模量和泊松比；Ei、νi分别为压头的弹性模量和泊松比；σy为弹塑性材料的屈服强度；σr为待检测材料的残余应力；n为材料的硬化指数；R为球形压头半径；h为压痕深度。

根据量纲分析和泊金汉定理可知

式中：Fm为压头施加最大载荷；Er为等效弹性模量，且

卸载段的载荷为

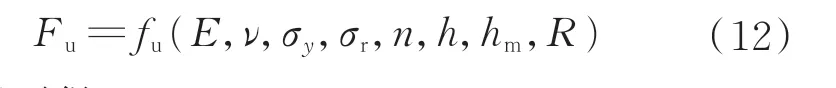
同理可得

定义不可逆功

因此，不可逆功与加载功的比值W为

假设在压痕过程中，材料受到平面二等轴残余应力且应力沿层深分布，在卸载过程中忽视残余应力的影响，则近似认为材料在压痕加载阶段为弹塑性变形过程，卸载阶段为弹性变形过程。通过Abaqus 模拟压痕状态下无量纲不可逆功W与等效应变、残余应力及硬化指数间的相互关系，得到的数据经过处理后，得出相互关系。根据不可逆功与等效应变、残余应力及硬化指数间的曲面关系，采用多项式函数拟合［7］，可得

式中：fi(i=1～10)与硬化指数n有关。

2 计算程序开发

从无量纲函数不可逆功W与等效应变、残余应力和硬化指数间的非线性函数关系，想要获得比较精确的全局最优解是比较困难的，所以我们使用人工神经网络来进行逼近曲面进行求解，计算出残余应力。为获取训练数据，可以使用有限元仿真分析完成。通常Abaqus 可以自动匹配合适的载荷增量和收敛准则，同时在仿真计算过程中持续调整这些参数值。压头半径为0.794 mm，将其作为解析刚体来处理，仿真过程中用一段弧线来表示接触面，被压材料尺寸为Φ 20 mm×10 mm；整个模型为轴对称模型，因此，可以进行相应的简化，简化后的模型绕Y轴旋转一周即为整个三维模型；同时为减小计算量对接触区域使用三节点单元进行网格划分，离接触区域较远的采用四节点的单元划分网格；在材料底部施加约束，限制Y轴上的运动，通过驱动压头压入材料，根据odb 文件中压头上的反作用力来取得载荷值，从相应的inp 文件取得位移值。

在压痕仿真过程中，设置不同材料弹塑性参数，不同的硬化指数和残余应力，其中E/σy∈(25，1 000)，σr/σy=±0.3、±0.6、±0.9。相应的数据处理后得出1 200 个数据对，900 个数据对进行神经网络训练，剩下的用于测试误差，部分训练数据见表1。

表1 部分神经网络训练数据Tab.1 Partial neural network training data

导入BP 神经网络进行训练，辨识残余应力。训练完成之后，使用剩下的数据，进行验算后发现，反演结果和参考数据对的误差可以控制在一定范围内，满足实际工程需要。因此，只需要从得到的载荷-位移曲线中获得压痕深度、加载功、卸载功、最大载荷、卸载斜率就能够计算出压痕处的残余应力大小，整个程序流程如图3 所示。最终编写的残余应力计算程序界面如图4 所示。

3 测量实验

使用经过改装的慢应变拉伸试验机对加工工件进行压痕试验，测量两组不同残留高度的平板工件，得到了镍铝青铜载荷位移数据，计算出残余应力大小。工件材料为铸造铜合金ZCuAl9Fe4Ni4Mn2，主要化学成分见表2。加工机床为拓璞VMC-C50五轴加工中心，刀具为仿形铣刀，直径25 mm，刀刃直径5 mm。压痕试验设备为慢应变速率应力腐蚀试验机4000，选用球形压头，直径为1.588 mm。通过外接力位传感器，以及对操控界面二次开发完成压痕加/卸载过程的数据采集。

图3 残余应力计算流程Fig.3 Process of residual stress calculation

图4 残余应力计算程序界面Fig.4 Interface of residual stress calculation program

表2 镍铝青铜材料的化学成分Tab.2 Chemical component of Ni-Al bronze material

工件1，如图5 所示，加工过程中铣刀转速458 r/min，每齿进给量0.09 mm，铣削宽度为2 mm，剪切角为25°。使用CAM 软件进行刀路规划时是使用残留高度来设置加工参数，所以实际加工中输入变量是残留高度，编号001 对应0.03 mm，编号002 对应0.09 mm，编号003 对应0.18 mm，其中A区域为单条刀路加工，B为交叉刀路加工。分别选择区域进行实验，A区域选择为单条刀路下的最低点为测量区域，随机选择8 条刀路，每个刀路测量一个点，B区域选择沟槽面的最低点为测量区域，随机选择8 个沟槽面，每个沟槽面一个点，之后得出相应的载荷-位移曲线。在数据分析时，去掉残余应力计算最大值和最小值，同时考虑神经网络计算过程中的误差情况，以及镍铝青铜材料力学性能，去掉与实际不符的数据，然后计算残余应力平均值，则A001的残余应力为160.49 MPa，A002 的残余应力为128.61 MPa，A003 的残余应力为144.68 MPa，B001的残余应力为139.57 MPa，B002 的残余应力为112.25 MPa，B003 的残余应力 为128.77 MPa。绘制残余应力和残高的关系曲线，如图6 所示，发现两条曲线趋势大致接近，也就是说残余应力计算程序可以预测铣削工件表面残余应力的趋势发展，能为加工工艺参数调控提供一定参考。

图5 不同行间距加工后的工件Fig.5 Workpieces machined at different line spacing

图6 残余应力随残留高度变化趋势Fig.6 Variation trend of residual stress with residual height

图7 不同主轴转速下的工件刀槽Fig.7 Workpiece slots at different spindle speeds

工件2，如图7 所示，进行单槽铣削加工，轴向切深0.9 mm，每齿进给量0.09 mm，主轴转速分别为229.18、458.37、840.34、1 222.31、1 833.46 r/min。如图6 画线区域压痕测试区每条槽测量2 个点，得出相应的载荷-位移曲线。最终取测量点平均值，测试结果见表3，其中主轴转速对残余应力的影响如图8 所示，随着主轴转速增加，残余拉应力有增大的趋势。

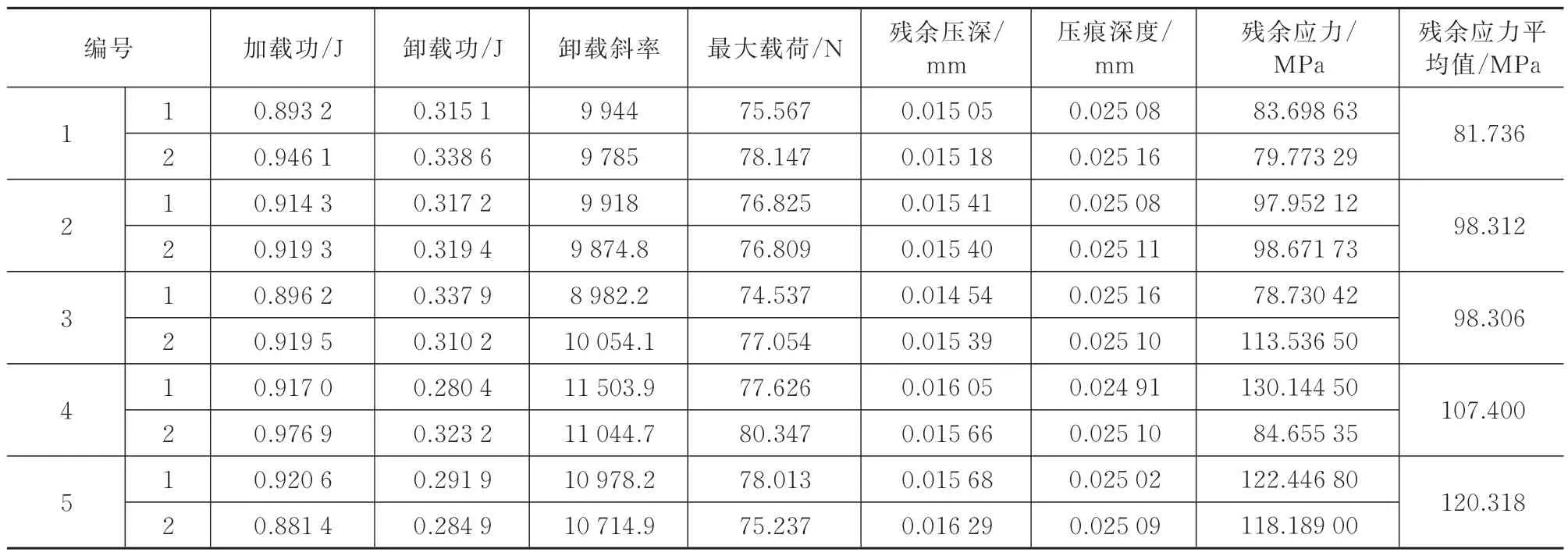
表3 不同凹槽下残余应力计算值Tab.3 Calculation values of residual stress under different slots

图8 主轴转速对残余应力的影响Fig.8 Effect of spindle speed on residual stress

4 结束语

在对镍铝青铜平板工件铣削过程中，改变残留高度，测量不同残高下残余应力变化水平，验证了基于压痕功残余应力测试方法的有效性；开展主轴转速对残余应力影响的实验，观察分析了随主轴转速的增加，工件表面残余应力的变化趋势。测试实验为桨叶铣削加工阶段切削参数优化调控提供了参考价值。后续，将测试仪器驱动控制—载荷位移数据采集—数据处理—残余应力计算集成为一个软件平台，提高交互性；同时为提高BP 神经网络计算精度，应增加训练数据对。