小学“数学广角”单元教学中的数学思想渗透
2020-06-29黄兆光
黄兆光


摘要:“数学广角”作为人教版数学教材编排的一大特色,其对发展学生的数学思想,培养学生的应用意识、解决实际问题的能力以及学生的数学核心素养,都有着积极的作用。文章以人教版五年级上册的“数学广角”——“植树问题”的教学为例,通过展示部分教学片断,分析如何利用“植树”问题向学生渗透建模思想,以使学生触类旁通、举一反三。
关键词:小学数学;“数学广角”;数学思想
一、小学“数学广角”单元教学内容的特点
“数学广角”这一单元内容是人教版数学教材的一大特色,从二年级到六年级,增设独立于“数与代数”“图形与几何”“统计与概率”“综合与实践”这四大板块的单元内容,它蕴藏着丰富的数学历史、数学知识以及数学思想。教材编者煞费苦心特意编排这一内容,旨在通过数学广角的教学,循序渐进地、系统地向学生更好地渗透相关的数学思想,引导学生发现数学与生活的紧密联系,培养学生的实际运用能力,促使数学核心素养的落实。
“数学广角”的教学内容比较灵活,兼具开放性与挑战性,并非简单计算便能得出答案,需要学生经历猜想、操作、验证等系列过程,这有利于学生的体验与感悟其中蕴含着的数学思想。此外,数学广角教学内容贴近现实生活,将复杂、抽象的数学思想寓于学生常见的生活情景中,既增强了数学教学的趣味性,又易于调动学生的学习兴趣,利于激发学生的好奇心和探究欲。
二、小学数学五年级上册“植树问题”中的数学模型思想渗透分析
模型思想是指从现实生活或具体情境中抽象出数学问题,用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律,换句话说,即将客观事物做抽象化的处理,从而建立起一个数学模型,根据这个数学模型有效分析事物本质规律的一种思维方法。
人教版五年级上册“数学广角”单元教学为“植树问题”,这一问题涉及“两端都植树”“一端植树”“两端都不植树”三种情况。
【教学片断一】
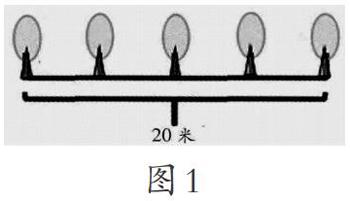
师:同学们,请看看屏幕上的这道题,大家会做吗?(多媒体出示题目:20米,每5米分一段,一共可分几段?)
生(大部分学生快速回答):4段。
师:正确,我们继续挑战,请继续看题。这题的答案又是多少呢?(多媒体出示题目:20米路,每5米种一棵树,一共可以种几棵树?)
生(多数):4棵。
生(少数):5棵。
师:有同学说4棵,有同学说5棵,到底谁正确呢?请看屏幕。(多媒体出示图1)
在备课时,笔者预测学生做“20米路,每5米种一棵树,一共可以种几棵树?”这道题时会出现两种不同答案,为此,笔者在实际教学中以此为契机,引发学生的认知冲突。另外,当出现两种不同的答案时,笔者先告诉学生正确的答案,却未告诉学生“为什么”,这有利于激发学生的求知欲,调动学生的主动性,促使其积极参与教学活动,主动探究新知。
【教学片断二】
师:正确答案是5棵。真奇怪,两道题目的表述好像都一样呀,为什么一个答案是4,一个答案是5呢?下面,请同学们以小组的形式来“找茬”,认真讨论这两道题的异同点在哪里。
(经过讨论,学生发表意见)
生:这两道题的相同点:都是平均分。这两道题的不同我们也找到了,前面一道题说的是“每5米分一段”,后面一道题说的是“每5米种一棵树”。
师:好,关于不同点,老师觉得可以再精准一点,不同点在于“一段”与“一棵树”,对吗?
生:对。
师:那“一段”与“一棵树”有什么不同呢?
生:“一段”有两个点,“树”是种在坑里的,所以“一棵树”相当于一个点。
师:按道理说,“一段”有两个点,“一棵树”才一个点,那是不是段数比点多呢?
师:两段有多少个点?三段呢?四段呢?五段呢?六段呢?—n段呢?
生:两段有三个点,三段有四个点,四段有五个点,五段有六个点。n段有n+1个点。
师:所以是点多还是段多?段数和点有什么关系?
生:点比段数多1,点=段数+1。
师:在植树问题里,“平均分的段”代表什么?
生:代表两棵树之间的间隔。
师:回答正确。所以,对于“20米路,每5米种一棵树,一共可以种几棵树?”这道题,我们应该怎么算?
生:20÷5+1=5(棵)。
师生齐总结:植树棵数=距离÷间隔+1。
在这一教学片断中,笔者首先引导学生明白,“植树”是植在点上,而不是植在段中;在此基础上,笔者通过循序渐进的提问,逐步引导学生发现“段”与“点”的关系——点=段数+1,并使学生明确“段”代表树与树之间的距离。这样,通过一连串问题的引导,学生在思考过程中不知不觉便在头脑中建立起了“植树问题”的模型思想:“植树棵数=距离÷间隔+1”。建立了这一模型思想后,对于“植树问题”,学生便能做到触类旁通、举一反三了。
【教学片断三】
师:同学们请看屏幕的这幅图,还是的同样的条件,在这种情况下,可以植多少棵树呢?(多媒体出示图2)
生:4棵。
师:怎么算的?可以用我们刚才学习的“植树棵数=距离-间隔+1”这个规律算吗?
生:就是用“植树棵数=距离÷间隔+1”这个规律算的,只不过算完之后要减去1,因为有一端被房子挡住了,不能种树。
师:那出现这种情况呢?可以种多少棵?同学们又是怎么计算的?(多媒体出示图3)
生:一共可以种3棵,还是可以用“植树棵数=距离÷间隔+1”这个规律来计算,只不过左右两端都被房子挡住了,所以算完之后需要减去2。
师:看来大家对植树问题的规律掌握得不错,能根据实际情况灵活变通运用。老师把同学们刚刚说的话重新整理一遍,大家仔细听,看老师说的对不对。一端能种树,一端不能种树的情况下,种树规律则为“植树棵数=距离-间隔+1-1”,也就是“植树棵数=距离÷间隔”;两端都被挡住,即两端都不种树的情况下,种树规律为“植树棵数=距离÷间隔+1-2”,也就是“植树棵数=距离÷间隔一1”。老师说清楚了吗?是不是这个意思?
生:对,就是这个意思。
师:好,老师想请同学们与老师一起来总结一下这三个种树规律,有信心吗?
师生齐总结:两端都种树:植树棵数=距离÷间隔+1。一端种树:植树棵数=距离÷间隔。两端都不种树:植树棵数=距离÷间隔-1。
在学生建立了一般植树问题的模型思想后,笔者逐步引申出植树问题的两种特殊情况,引导学生在运用植树问题模型思想解决问题的过程中,总结出“一端植树”和“两端都不植树”的数学规律。另外,在教学时,笔者用简练的语言复述学生的话,并请学生判断笔者说得对不对,这有利于集中學生的注意力,促使学生积极参与课堂教学;而最后师生齐总结三种不同的植树方式的规律时,有利于学生整理自己的思绪,回顾教学内容,巩固新知。
【教学片断四】
师:植树问题规律可以运用在其他地方吗?
生1:路灯的安装。
生2:公交站的设定。
生3:锯木头也可以用,属于两端都不种树的情况。
生4:爬楼梯是属于一端种树的情况。
模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。笔者让学生通过头脑风暴的形式,把植树问题的模型思想与生活联系起来,引导学生发现数学知识与生活联系的紧密性,让学生学会学以致用,将理论与实践结合起来。
三、结语
人教版小学数学中“数学广角”的教学内容,紧贴生活实际,虽然教起来有一定的难度,但其蕴含着丰富的数学思想,教师需要予以重视,不可因其难教便敷衍了事,不仅需要精心研读教材,更要做到“备学生”,引领学生经历“观察、分析、归纳、推理”等活动,使学生从中感悟到相关的数学思想,并灵活运用数学思想。
参考文献
[1]中华人民共和国教育部.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
[2]蒙泽颖.小学高年级“数学广角”单元渗透数学思想方法的教学策略研究——以人教版教材为个案[D].贵阳:贵州师范大学,2019.
