基于首次穿越时间概率密度的时变可靠性分析

俞 水，汪忠来

(电子科技大学 机械与电气工程学院，成都 611731)

1 引 言

在机械产品的寿命周期内，产品的材料性能、工作环境和载荷效应等呈现时变性和非线性，这将给产品的可靠性分析和设计带来新的挑战。由于传统的静态可靠性分析方法[1-3]忽略了时变不确定性对可靠性的影响，从而无法获得满足精度的可靠度。因此，针对产品的时变不确定性进行时变可靠性分析具有重要的工程意义。

时变可靠性分析是目前可靠性分析和设计的热点问题，已有大量的研究工作，主要可以分为解析法和数值仿真法两类。数值仿真方法利用随机过程时间序列离散，将时变可靠性问题转化成高维的静态可靠性问题，主要包括蒙特卡洛仿真方法[4]、重要度抽样技术[5]和子集模拟[6]。蒙特卡洛仿真虽然可以获得精确解，但是针对高可靠度评估问题计算效率极低，因此常将蒙特卡洛仿真方法作为评价其他可靠度分析方法的一个标准。重要度抽样技术在处理高维性能函数时往往无法给定合适的重要性抽样密度，而且重要度抽样密度的选择依赖于时效域的相关信息。子集模拟是最近出现的高可靠度评估的有效方法，但其计算效率取决于性能函数的线性程度。此外，国内外学者从解析法的角度开展了大量的研究工作，主要包括极值响应面方法[7]、Gamma过程[8]、复合随机过程法[9]、摄动法[10]、复合极限状态法[11]和穿越率方法[12]。极值响应面方法、Gamma过程和复合随机法在评估时变可靠性时需要假设系统参数或者性能服从特定的分布，将产生模型近似误差；摄动法对系统参数有较强的依赖性；复合极限状态法在处理非线性程度较高的性能函数时，将产生无法接受的误差；相对而言，穿越率方法在计算效率方面优势较大，引起学术界和工业界的广泛关注。Rice[12]首先提出了穿越率方法，随后许多学者在此基础上开展了大量的研究，主要包括可微高斯过程法[13]、矩形波更新过程法[14]、拉普拉斯积分法[15]、PHI2方法[16]和PHI2+方法[17]。由于近似时间积分的复杂性和泊松分布假设，可微高斯过程法、矩形波更新过程法和拉普拉斯积分法只能处理特定随机过程条件下的穿越率计算问题，且计算精度不高。PHI2和PHI2+方法利用并联系统可靠性框架来提高计算精度以及扩宽穿越率计算方法的适用范围。但现有研究表明，在处理非单调性系统时，基于并联系统可靠性框架的穿越率计算方法显现出较低的计算精度[18]。

本文针对产品全寿命周期的时变可靠性问题，建立了首次穿越点的概率分布模型，提出了一种求解时变可靠性的计算方法，可获得产品在寿命周期内的可靠性累计概率密度函数。

2 时变可靠性简介

时变可靠性是指产品在规定的时间内和条件下承受时变不确定性作用能够完成规定功能的概率。因此在寿命周期[0,T]内，产品的可靠度R(0,T)可以表示为

R(0,T)=Pr{g(X,Y(t),t)>0,∀t∈[0,T]}

(1)

式中X是n维随机变量向量，Y(t)是m维随机过程向量，g是产品的性能函数。

因此，产品在寿命周期内的失效概率为

P(0,T)=Pr{g(X,Y(t),t)≤0,∃t∈[0,T]}

(2)

3 基于首次穿越时间概率模型的时变可靠性分析

穿越率方法已经成为产品时变可靠性评估的主流方法，首先基于一些随机过程的假设来计算穿越率，然后利用穿越率估计可靠度或者失效概率是穿越率法的一般流程。然而，由于穿越率计算时的随机过程假设，导致了该方法目前仅能针对少数几类特殊形式的性能函数给出有效的穿越率计算方法，而对于一般类型的性能函数，采用蒙特卡洛计算穿越率效率极低。为此，本文提出了一种基于首次穿越时间概率模型的新型时变可靠性分析方法(F-PTPD方法)。

3.1 基于首次穿越时间概率密度函数的转化模型

为了简化计算过程，输入随机过程向量Y(t)通过离散随机过程方法[19]分解成随机向量Y*和时间t的耦合函数。因此，性能函数变为随机变量向量和时间t的函数，不妨设为g(Z,t)，其中，Z=(X,Y*)。

当赋予性能函数输入随机变量其自身分布的样本值Z时，性能函数视为关于时间t的一元函数，图1展示了样本值Z和其相对应的性能g(Z,t)的关系。

如图1所示，g(Z,t)与时间轴的三个交点分别是t1，t2和t3，称第一个交点t1为首次穿越点。首次穿越点与寿命周期[0,T]的位置关系决定了当输入为Z时产品的失效情况。如图1(a)所示，t1>T时，产品可靠；反之，如图1(b)所示，当t1∈[0,T]时，产品失效。根据产品性能函数g(Z,t)可知，首次穿越点是输入随机变量的函数，记为t1=t(Z)。则产品在寿命周期[0,T]的失效概率可以表示为

P(0,T)=Pr{t1∈[0,T]}

(3)

对于首次穿越点函数t1=t(Z)，若已知其概率密度函数f(τ)，则式(3)所示的产品失效概率可以转化为

(4)

3.2 首次穿越时间的概率密度函数

由于不同产品性能函数不同，而且复杂产品的性能函数维度和非线性程度较高，导致无法直接利用g(Z,t)=0来求解首次穿越点。因此，利用将性能函数在性能函数均值函数的首次穿越点处二阶泰勒展开为关于时间的二次函数，利用二次函数的性质来求解首次穿越点与输入变量的函数关系；再利用稀疏网络随机配置方法[20]得到首次穿越点的四阶原点矩；基于首次穿越点的四阶原点矩，采用最大熵估计方法来估计首次穿越时间的概率密度函数。

3.2.1 首次穿越点函数的求解

根据随机过程均值函数定义，性能函数g(Z,t)的均值函数可以表达为

(5)

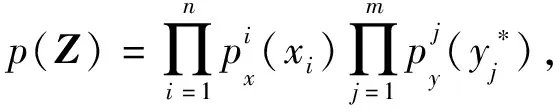
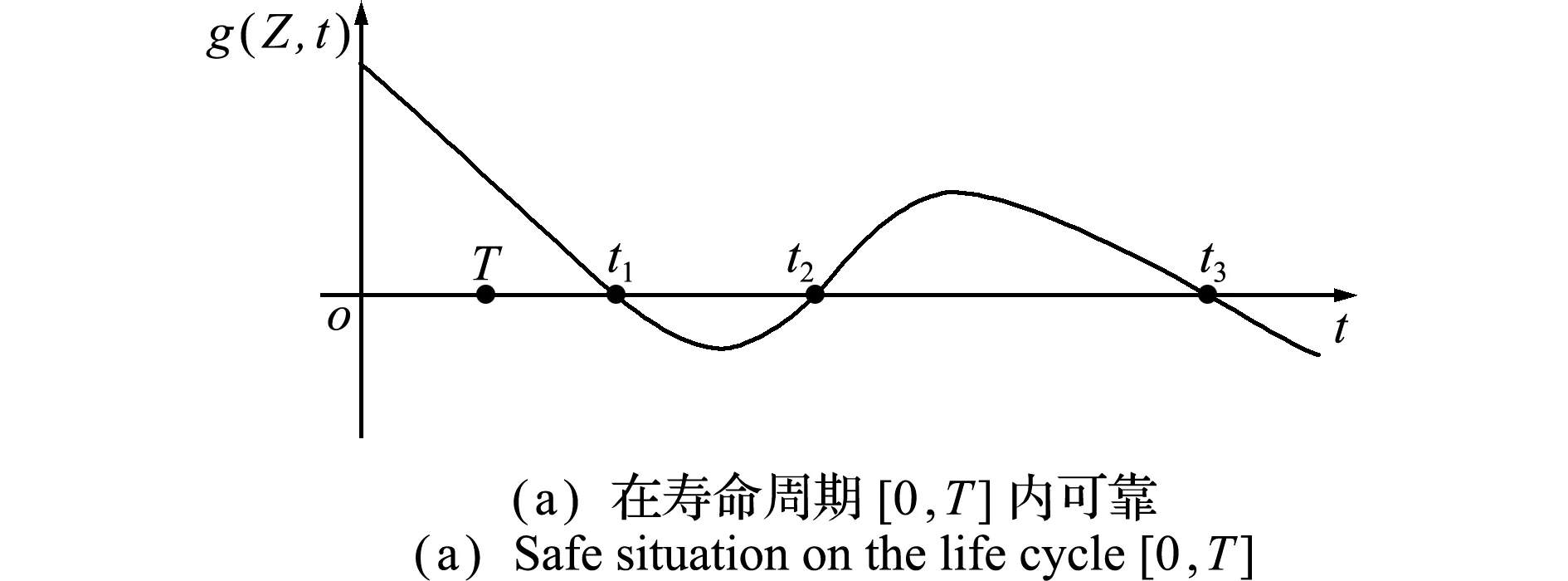
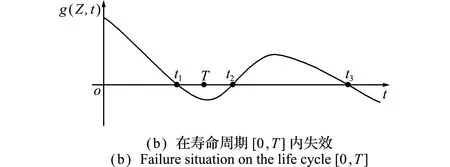
图1Z和其相对应的性能函数g(Z,t)的关系

Fig.1 Geometrical relationship betweeng(Z,t)andZ

(6)

对于式(6)的多重积分模型，利用稀疏网络随机配置方法来执行均值函数的计算。根据稀疏网络随机配置方法的特点，本文假设所有的输入随机变量均服从相互独立的标准正态分布，否则利用Rosenblatt变换[20]将其他分布类型转化成为相互独立的标准正态分布。基于Smolyak算法[20]，利用稀疏网络随机配置来计算式(6)的多重积分：

(7)

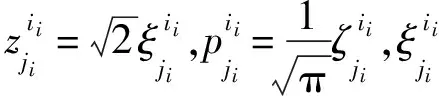
(8)

式中q值取决于性能函数的非线性程度，在实际工程中为了保证计算效率和精度，取2≤q≤4。

当输入变量积分点产生后，式(7)就是关于时间t的函数，即性能函数的均值函数。因此，均值函数的首次穿越点可由μ(t)=0获得，记为t*。将性能函数g(Z,t)在均值函数的首次穿越点t*处二阶泰勒展开为

(9)

3.2.2 首次穿越点的概率密度函数

当获得首次穿越点关于输入随机变量的函数t1=t(Z)后，首次穿越点的四阶原点矩可以表达为

(10)

利用稀疏网络随机配置来估计式(10)的多重积分，计算过程和均值函数计算过程相同。于是，得到首次穿越点的四阶原点矩M1,…,M4。基于四阶原点矩利用最大熵方法来估计首次穿越点的概率密度函数，首次穿越点的概率密度函数f(τ)可由最大熵模型(11)获得。

(11)

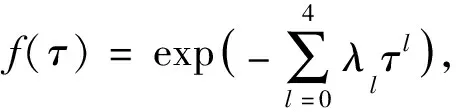
(12)

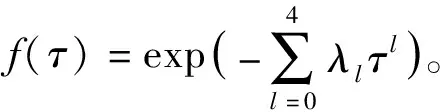
3.3 基于首次穿越点概率模型的时变可靠性分析

由稀疏网络随机配置法和最大熵概率密度估计方法可以得到首次穿越点的概率密度函数，因此在寿命周期[0,T]的可靠度可以表示为

(13)

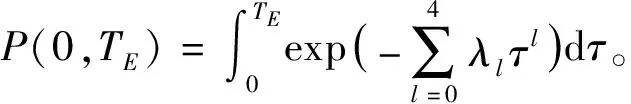
F-PTPD方法流程如图2所示，具体步骤如下。

(1)随机过程离散。根据输入随机过程信息，将输入随机过程向量Y(t)通过离散随机过程方法转化成随机向量Y*和时间t的耦合函数。

(2)求解均值函数首次穿越点。采用稀疏网络随机配置方法求解性能函数均值函数μ(t),并通过求解方程μ(t)=0获得均值函数首次穿越点t*。

(3)确定性能函数首次穿越点函数。通过对性能函数在t*二阶泰勒展开，并利用一元二次函数求根方法，求得性能函数首次穿越点函数t1=t(Z)。

(4)获得性能函数首次穿越点概率密度函数。利用稀疏网络随机配置方法结合最大熵概率密度估计方法，可获得性能函数首次穿越点概率密度函数f(τ)。

(5)时变可靠性计算。对概率密度函数f(τ)积分，可得到寿命周期[0,T]的可靠度。

4 数值算例

算例1考虑性能函数(14)

(14)

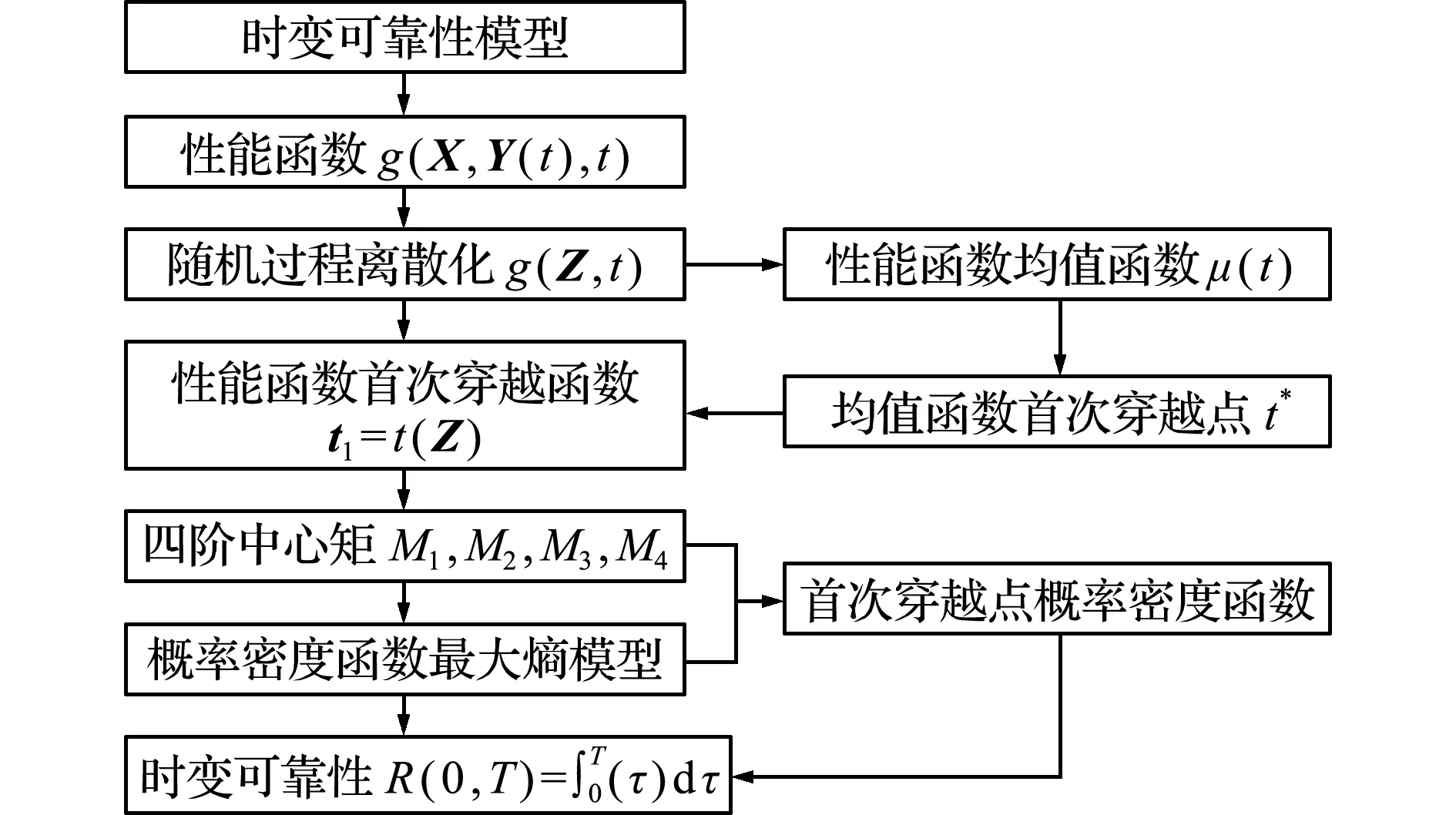
图2 F-PTPD方法的流程

Fig.2 Flowchart of F-PTPD method

式中X1和X2均服从正态分布，且X1～N(5,0.25),X2～N(5,0.25)。图3为利用本文方法得到的首次穿越点的概率密度函数。图4为由本文方法得到的概率密度函数通过对产品服役时间的积分求得产品时变失效概率的变化趋势，同时也展示了作为参考的蒙特卡洛方法估算的时变失效概率。可以看出，两种方法所得结果非常接近，说明由本文方法能够精确地估计产品寿命周期的时变失效概率的变化趋势。

此外，在利用随机网络系数配置法来估计性能函数均值函数和首次穿越点原点矩时，取q=3,于是可产生13个输入样本，同时算例1利用前四阶原点矩和最大熵优化模型来估计概率密度函数，求解最大熵优化模型需要迭代约20次，因此利用本文方法来估计首次穿点概率密度函数的函数调用次数为13+13×20=273。在蒙特卡洛仿真过程中，输入随机变量的样本个数为105，此外，在估计每段时间区间可靠度时，取时间间隔为0.01。如在利用蒙特卡洛仿真来估计时间区间[0,15]的时变可靠度时，需要函数调用次数为105×15×100=1.5×108。本文方法只需273次函数调用就可以得到产品寿命周期关于时间的概率密度函数，然后通过一次积分运算就可以得到任意区间的失效概率，然而，在利用蒙特卡洛仿真计算时间区间[0,T]的失效概率时，需要107×T次函数调用。可以看出，本文方法能够在保证精度的前提下极大地提高时变失效概率的评估效率。

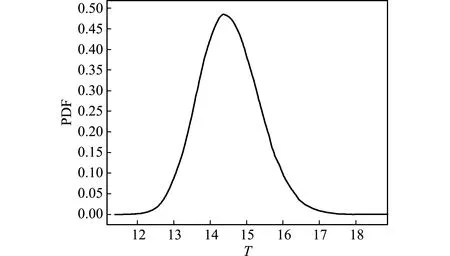
图3 算例1首次穿越点概率密度函数

Fig.3 Probability density of first-passage time point for the example 1

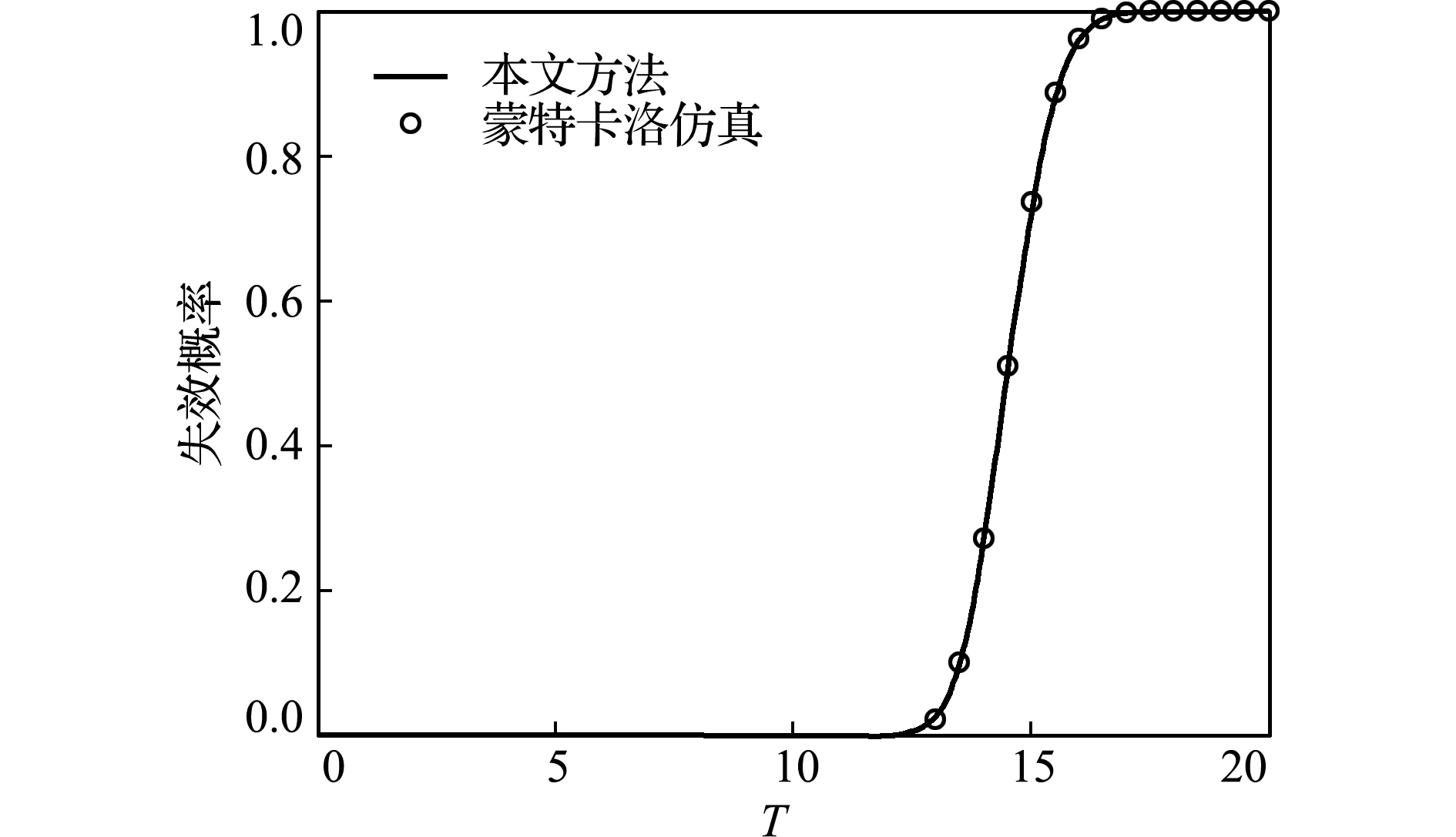
图4 算例1的时变失效概率

Fig.4 Time-dependent failure probability for the example 1

算例2图5为一悬臂梁结构，其中，长度L=5 m，界面是宽为b0，高为h0的矩形，且b0和h0均为随机变量。材料密度为ρ=7.85 kg/m3,屈服强度为σ。该简支梁中点承受集中随机载荷F(t)和均匀分布载荷p的作用，其中随机载荷F(t)是均值为3500 N、变异系数为0.2、自相关函数为exp[-(3τ)2]的高斯过程；均匀分布载荷p可以表示为ρgb0h0。

该悬臂梁从t=0时刻开始腐蚀，且在整个截面上腐蚀程度各向同性，同时腐蚀部分完全失去机械强度，则未腐蚀部分的面积表示为

A(t)=b(t)×h(t)

(15)

式中b(t)=b0-2κt,h(t)=h0-2κt,κ=0.03 mm/年。当应力达到材料的极限应力时，该简支梁发生失效，于是，性能函数可以表达为

g(X,Y(t),t)=σb(t)h(t)2/4-[F(t)L/4+

ρb(t)h(t)L2/8]

(16)

该悬臂梁的随机分布信息列入表1。图6给出了由本文方法所估计得到的悬臂梁的概率密度函数，该悬臂梁在服役期间的失效概率变化趋势如图7所示，同时图7包含了蒙特卡洛仿真结果。可以看出，两种方法得到的结果非常接近，这说明本文方法能够在提高计算效率的同时保证估计结果的精确性。

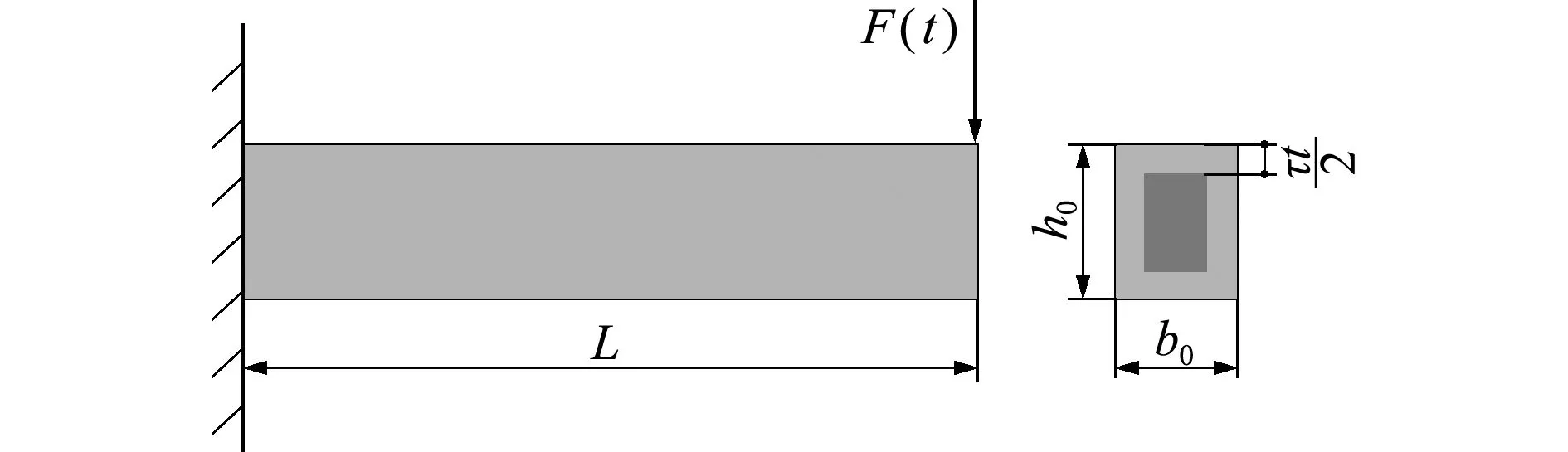
图5 悬臂梁

Fig.5 Cantilever beam

表1 简支梁的随机参数分布

Tab.1 Distribution information of cantilever beam

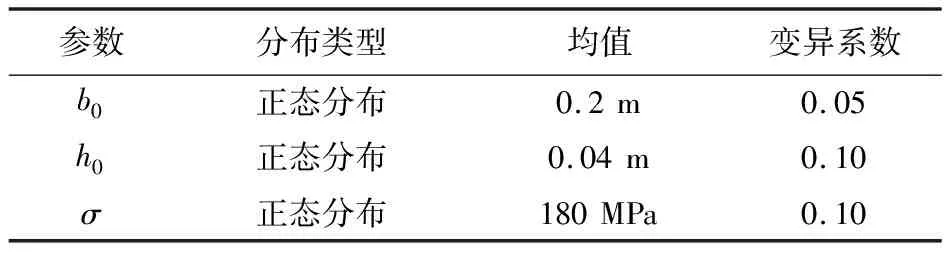
参数分布类型均值变异系数b0正态分布0.2m0.05h0正态分布0.04m0.10σ正态分布180MPa0.10

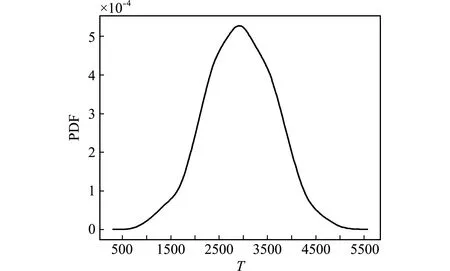
图6 算例2的首次穿越点概率密度函数

Fig.6 Probability density of first-passage time point for the example 2

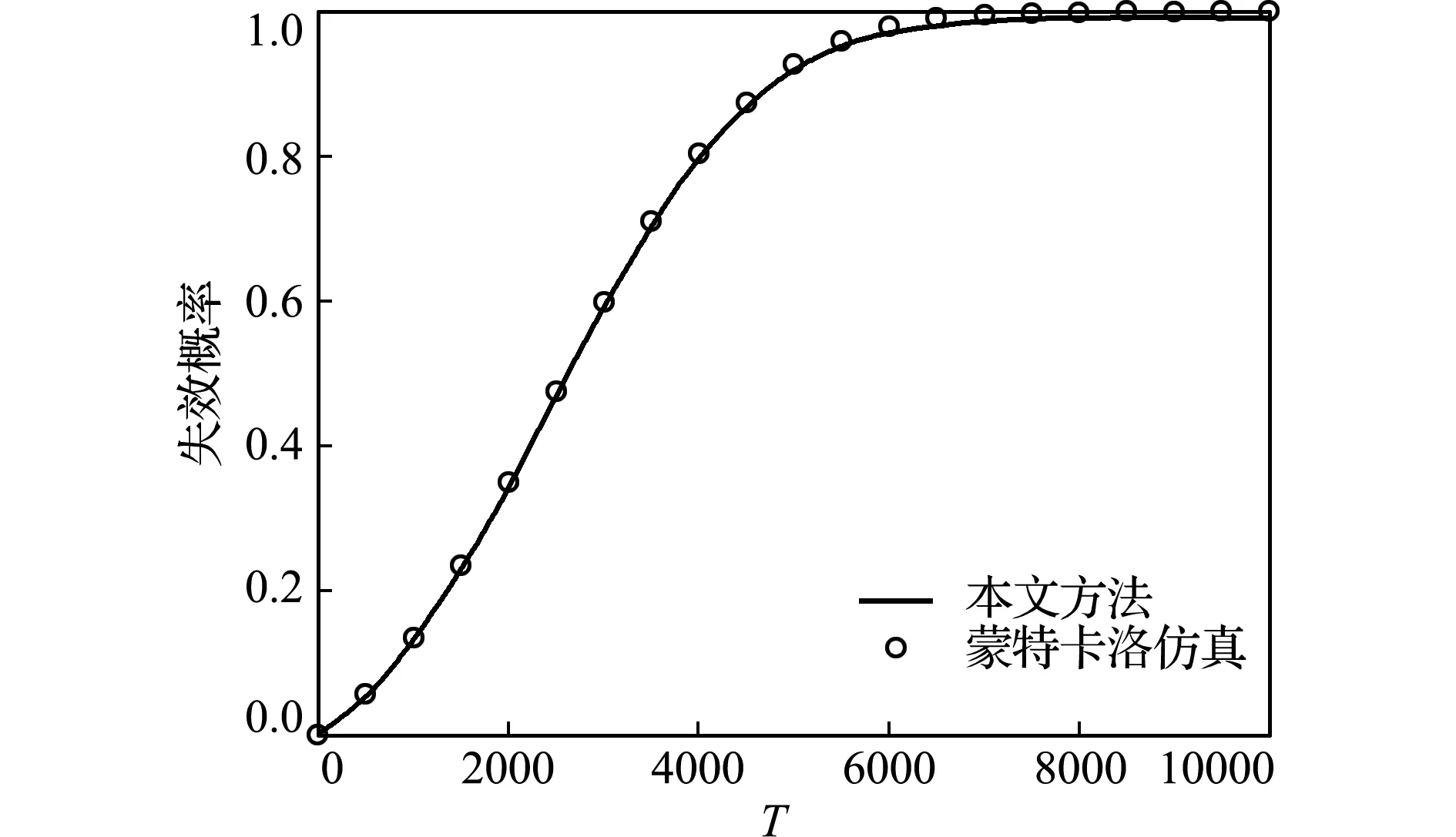
图7 算例2的时变失效概率

Fig.7 Time-dependent failure probability for the example 2

5 结 论

本文基于对产品性能函数的分解，利用稀疏网络随机配置方法和最大熵方法估计性能函数首次穿越点的概率密度函数，提出一种求解时变可靠性的方法，可获得产品整个寿命周期时变失效概率的变化趋势。通过对性能函数二阶泰勒展开，将性能函数分解成关于时间的二次函数；利用二次方程求根公式得到性能函数首次穿越点关于输入随机变量的函数表达式；采用稀疏网络随机配置方法和最大熵方法估算首次穿越点的概率密度函数。与传统的时变可靠性评估方法相比，本文方法可获得产品整个寿命周期失效概率的变化趋势，而不是某个时间区间，极大地提高了评估效率，对复杂产品的可靠性评估设计有一定的工程指导意义。同时两个算例表明，该方法的精度满足工程需求。