多因素限制下的管制间隔相似性

杜 实， 王利航， 任景瑞， 闫 丹

(1.中国民航大学空中交通管理学院，天津 300300；2.中国民航大学飞行技术学院，天津 300300)

2018年，中国民航全行业运输航空公司完成运输469.47×104架次，比上年增长7.6%[1]。中国持续、迅速增长的民航业，给居民出行和生活提供了便利，同时也给管制部门带来了空前的压力。

空中交通管制的核心任务是保障航空器的安全运行，实现这一目标的方法与手段是为航空器之间配备安全间隔[2]。管制员在调配航空器时，由于个人技术和间隔使用习惯的差异，对安全和效率有较大的影响。故而，对间隔使用情况及其规律的掌握非常必要。

关于管制间隔的研究已有大量报道。杨新湦等[3]、赵宁宁等[4]研究了航路上管制间隔与碰撞风险计算的问题；王莉莉等[5]研究了航路间隔调整问题，提出了对应的间隔调配方案；杜实等[6]分析了管制间隔的影响因素，建立了多因素关联模型并得到各因素的影响指数。前人研究主要集中在管制间隔影响因素及碰撞风险等方面，对管制员技术特征研究与管制员使用管制间隔特性的关联性研究很少。

对于相似性的研究，中外交通运输领域内研究大多集中在公路、铁路等交通流的识别以及发展趋势的预测等。张晚笛等[7]利用地铁乘客数据来分析不同时间序列下居民地铁出行规律的相似性，得到了客流时间序列模型和相似性度量方法；黄何列等[8]提出了一种新的度量交通流相似性的准则——最大偏差相似性准则以及相应的聚类算法；Habtemichael等[9]提出了一种基于加权欧氏距离改进的K-最近邻算法识别相似交通流模式的短期流量预测算法，并使用高速公路流量数据进行仿真验证；弓晋丽等[10]利用分层聚类算法比较不同时间序列识别交通流状态的结果，确定出最佳交通流模式相似性度量方法；李星毅[11]采用相似性特征分析方法来挖掘城市公路交通流可能蕴含的模式,并依据数据与模式之间的关系来评价交通流状态、分析预测交通流发展趋势。在民航领域内，相似性研究较少，尤其鲜少有关于航空器间隔的相似性研究。

研究管制运行间隔的相似性，是为了分析管制员航空器间隔使用特性的异同，掌握管制员工作模式及管制水平的差异点，将对于提高管制员能力水平、规范管制员工作行为、降低管制工作负荷的研究与决策工作有一定的支持作用，为空中交通安全、高效地运行提供保障。

1 数据处理与间隔计算

采用的数据是2018年6月—8月珠海终端区部分时段的航班数据，包括往来于澳门国际机场、深圳宝安国际机场、珠海金湾机场的数据。主要研究深圳机场的进场航空器之间的间隔值，使用MATLAB等软件对获取数据进行清洗与归约计算。

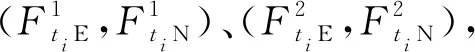
(1)

式(1)中：D为两架航空器之间水平距离，即航空器对的即时间隔或称作它们的雷达管制运行间隔,简称间隔。

利用式(1)进行间隔计算，同时对间隔数据进行归约处理并计算各间隔值的使用比例情况。在获得间隔值数据后，对其进行统计分析，期望发现其中的规律，为了得到初步的直观认识，将间隔值变化及其使用比例情况绘制在图中，选取6月16—19日的间隔数据进行绘制，如图1、图2所示。

图1 连续4 d的间隔值变化Fig.1 Change of consecutive four-day’s separation value

图2 连续4 d的每天间隔使用比例图Fig.2 Consecutive four-day’s daily separation usage proportion chart

由图1可以看出航空器的间隔值变化趋势有较为明显的分簇情况，即部分航空器间隔值变化在某种程度上是一致的。由图2可以看出，间隔的使用比例曲线变化趋势大体类似，同时也略有差异，可见其中蕴含着某种相似性，需要进行深入挖掘。将上述日期的间隔使用比例情况绘制在同一坐标系中，如图3所示，可以看出管制间隔使用比例曲线呈较高的重合度。

图3 连续4 d的间隔使用比例绘制在同一坐标系Fig.3 Consecutive four-day’s separation usage proportion draw in the same coordinate system

2 间隔相似性判据

根据第1节初步分析可以在直观上看出管制员在使用管制间隔时有一定的相似性，为了更好地量化这种特性，对这种客观规律进行科学表达，采取相似系数S和波动系数ξ来进行量化，根据两个系数的值的大小来判断相似性[12]。

2.1 相似系数

以研究的每天08:00—10:00的数据为对象，设为一个列向量pi，将所研究日的数据构成矩阵P=[p1,p2,…,pn]。定义相似系数S为各向量两两之间相关系数的均值，即：

(2)

式(2)中：R为矩阵P的相关系数阵，有：

R(i,j)=R(j,i)=

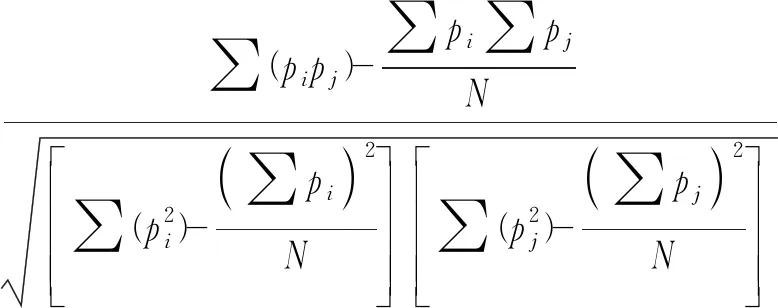
(3)

式(3)中：N为实际管制员使用具体间隔值的数量。

S越大，表明管制员使用相似间隔比例越高。此外，还要意识到在上述处理中没有考虑航班架次的影响，即以上所计算的S仅表明在没有涉及航班数量特征时管制员使用间隔比例的相似性。为了保证S的准确性，真实反映航班运行的特征，需要在求其数值之前确保所研究时段内航班构成是相同的或相似的。因此，再定义波动系数ξ，以此来判断航班架次是否具有相似性。

2.2 波动系数

令向量M=[E(P1),E(P2),…,E(Pi)]，其中M的每个元素代表第i(1≤i≤n)天08:00—10:00每10 min时间段内航班架次的均值。定义波动系数ξ为

(4)

式(4)中：D(M)为M的方差；E(M)为M的均值。ξ越小，表明各天平均航班架次的变化程度越小。结合研究数据以及实际情况，设定当ξ<0.05，则认为各天平均航班架次在绝对数值上具有相似性。

3 相似性分析

在民用航空运营中，每周的航班主体按照航班时刻表是不变的，因而相同的“周几”的航班架次、航班构成等基本一致。在实际运行中，因天气等影响因素作用，航班运行时间可能会有前后移动，但总体变化不大；在数量上可能会有加班、包机等变数，但占比较少，在间隔值计算上可忽略不计。在考虑天气因素之后，选取天气情况相近的几个类似的“周几”可以基本保证航班架次等外界要素的一致性，使得研究更加严谨可靠。在统计了每天 08:00—10:00的航班架次后，分别提取了几个周一以及连续几天的数据来进行研究，按照两个方向来进行间隔特性分析：①同一班组管制员在两个“类似”周一和不同班组管制员在连续的两个“类似”周一的管制间隔使用的特性；②同一班组管制员在三个“类似”周一和三个连续的“类似”的日历日管制间隔使用的特性。

“类似”日的数据指的是为保证管制间隔使用特性具有研究价值而选取的航班架次、航班构成、天气情况等要素差别不大日期的数据。

在保证航班架次具有较小差异的基础上，针对上述两个方向分别采用了6月25日、7月2日、7月23日3天的数据以及6月18日、7月16日、7月30日、7月31日、8月1日、8月13日6天的数据。为便于表示和计算，将所有日期的管制间隔使用比例数据按照日期的先后顺序，分别设为向量p1,p2,…，p9；依据第2节公式的设定，i表示第i天，i=1, 2, …，9；统计航班架次的时间间隔为10 min，则每天数据的序列长度为12。

依据实际工作中管制员轮流排班的情况，可以知道对于每天的08:00—10:00，6月25日与7月23日为同一班组管制员值班，6月25日与7月2日为不同班组管制员值班；6月18日、7月16日与8月13日为同一班组管制员值班，7月30日、7月31日与8月1日为不同班组管制员值班。

3.1 “类似”周一间隔特性分析

将6月25日、7月2日和7月23日3 d的数据向量构成矩阵P1=[p2,p3,p5]，则可得相关系数矩阵：

(5)

三个周一的天气情况和部分航班进场顺序情况如表1、表2所示。相似性计算结果如表3所示。对应管制间隔使用比例如图4、图5所示。

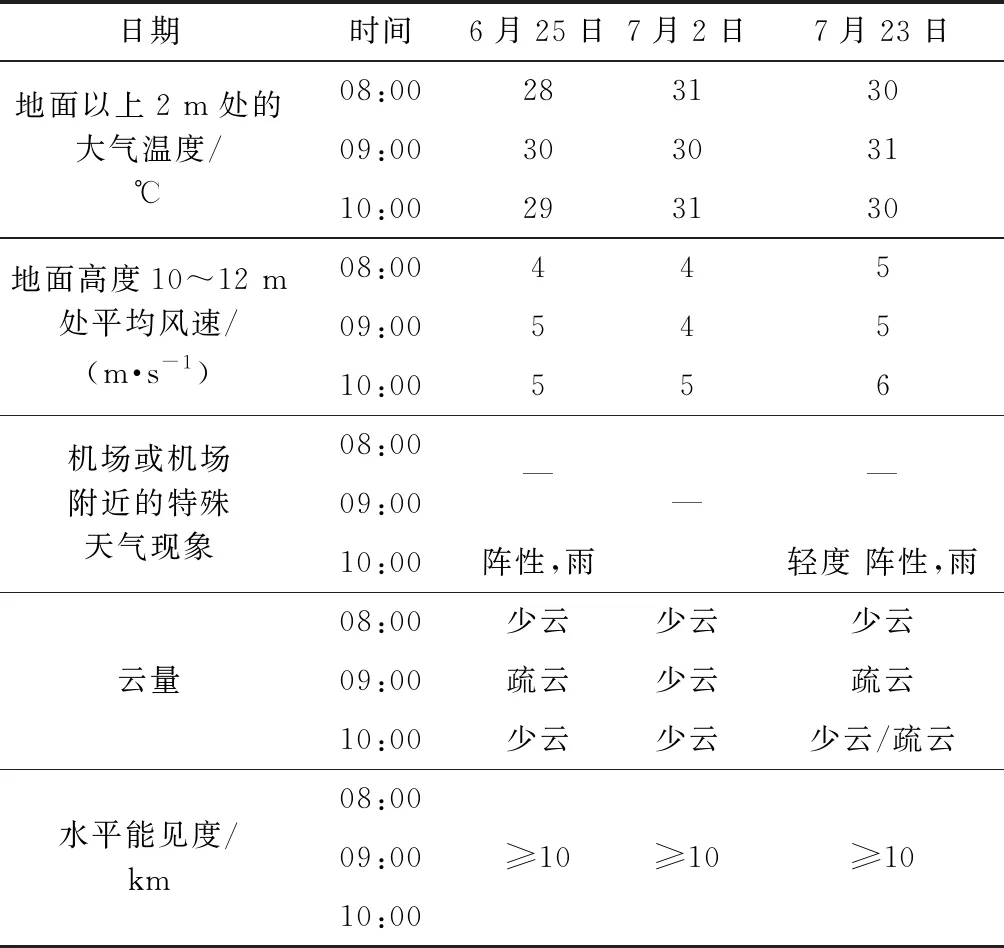
表1 6月25日、7月2日和7月23日天气情况Table 1 Weather conditions on June 25,July 2 and July 23

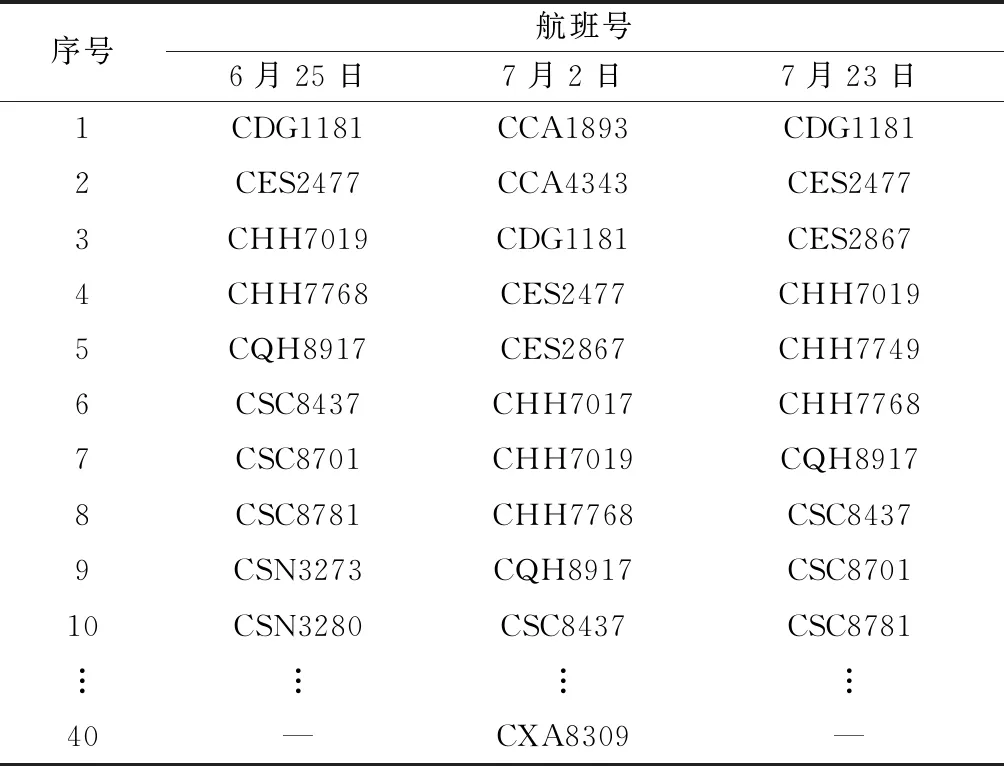
表2 6月25日、7月2日和7月23日部分航班进场顺序Table 2 Arrival sequence of partial flights on June 25,July 2 and July 23

注：在所研究的时段内，6月25日航班数量为39，7月2日航班数量为40，7月23日航班数量为39。

表3 三个周一的相似性分析Table 3 Three Mondays’ similarity analysis

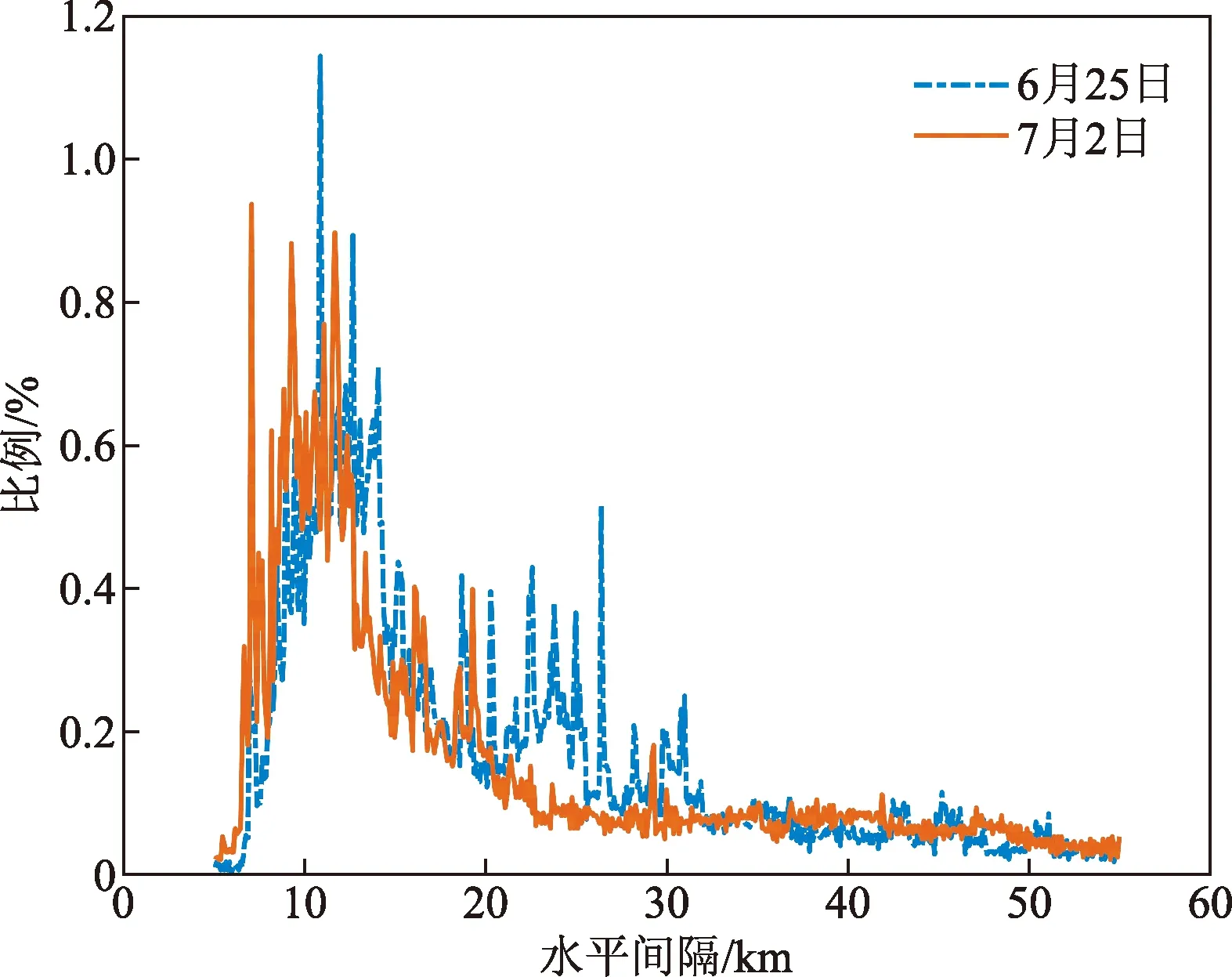
图4 6月25日与7月2日间隔使用比例Fig.4 Proportion of separation on June 25 and July 2

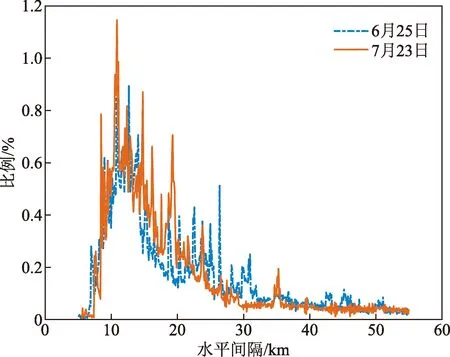
图5 6月25日与7月23日间隔使用比例Fig.5 Proportion of separation on June 25 and July 23

相关系数矩阵中的相似系数，计算的是两两向量之间的相似系数，即n=2，因此[pi,pj]两向量之间的相似系数S即为R(pi,pj)，如P12=[p2,p3]，那么对应的S12=R1(1, 2)=0.779 8，以此类推。

根据表1给出的天气情况，可以看到3 d的大气温度、平均风速、云量、水平能见度等比较接近，机场或机场附近的特殊天气现象中，6月25日与7月23日均在10：00左右有轻微阵性降雨，对航班影响程度较小；3 d的航班构成及进场顺序略有不同，但整体差别不大；再结合表3给出的分析结果，可以看到6月25日与7月23日和6月25日与7月2日两天数据波动系数ξ均较小，表明平均航班架次的绝对值接近，则可以认为3 d的航班运行情况较为一致。

同一班组的6月25日与7月23日的间隔使用相似系数S为0.859 9，管制间隔使用相似性较高；而不同班组的6月25日与7月2日的间隔使用相似系数S为0.779 8，相对较小，即同一班组管制员相较不同班组管制员在航班运行情况较为一致的日期中管制间隔使用上相似性较高。同时分析图4、图5给出不同日期的管制间隔使用比例绘制在同一坐标系中曲线的重合情况，也可以看出，6月25日与7月23日的曲线重合度相对6月25日与7月2日的曲线重合度而言较高，即表明前者的相似性更高，证实了前面的判断。

3.2 连续日与“类似”周一间隔相似性

选取的连续日与“类似”周一的天气情况都基本相似，均无影响航班运行的重要天气情况，且航班构成也大体一致，因此不再赘述相关日期的天气和航班构成情况。

3.2.1 连续3 d间隔特性分析

选取7月30日、7月31日和8月1日连续3 d的数据，这3 d为不同班组管制员值班，将3 d的管制间隔使用比例数据构成矩阵P2=[p6,p7,p8]，则可得相关系数矩阵如下：

(6)

相似性计算结果如表4所示。对应连续3 d的管制间隔使用情况如图6所示。

表4 连续3 d的相似性分析Table 4 Secutive three-day’s similarity analysis

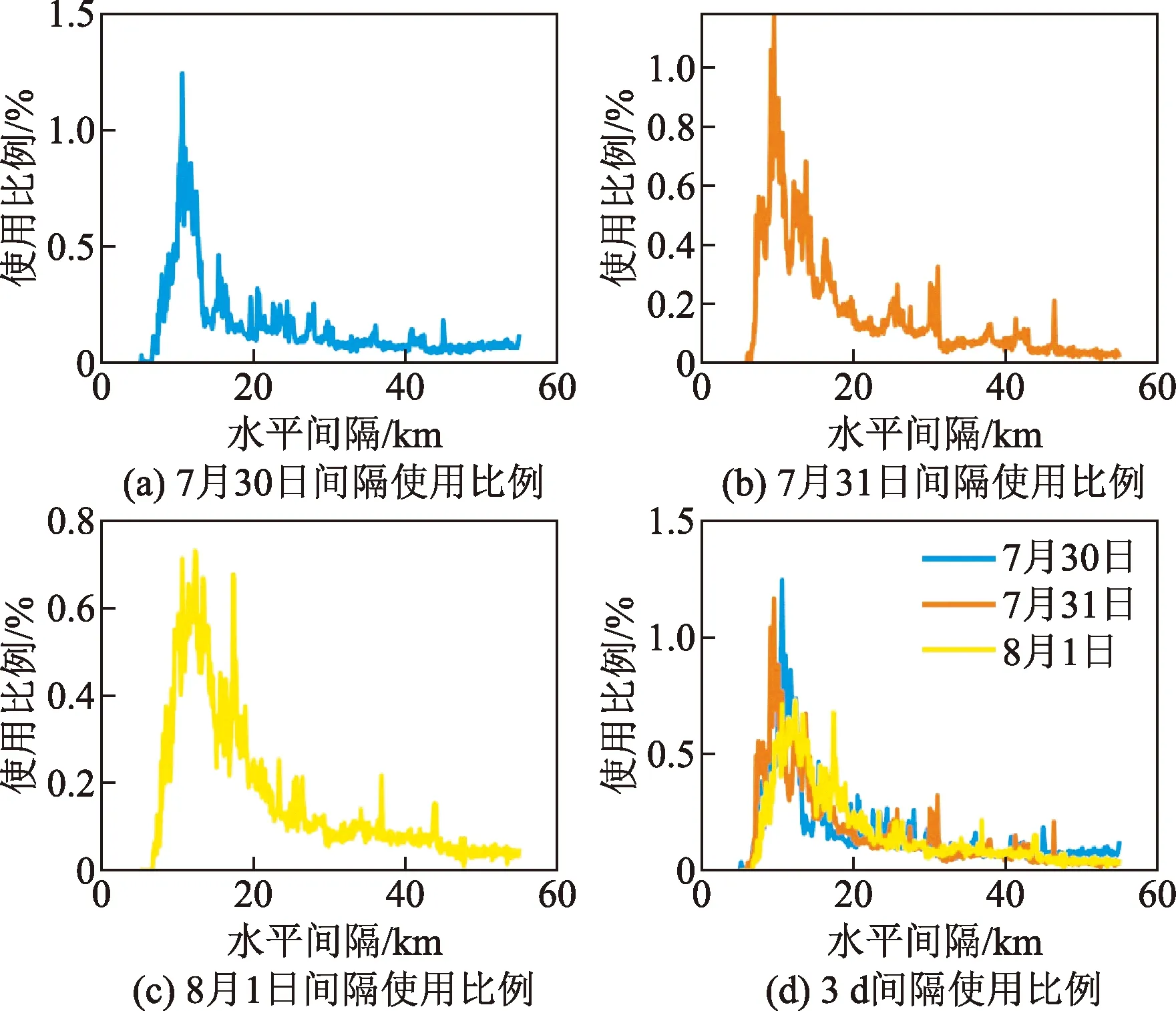
图6 连续3 d的管制间隔使用比例Fig.6 Secutive three-day’s control separation usage proportion

根据表4中计算结果的相似系数可以知道，在不同班组管制员值班时，管制间隔的使用相似性相对较小；同时分析对应的管制间隔使用比例图可以发现，连续3 d每天的曲线变化趋势差异相对较大，绘制在同一坐标系中重合度也相对较低，即这3 d管制员管制间隔使用相似性相对较低，可见不同班组管制员在使用管制间隔时在一定程度上分别有自己的管制习惯。

3.2.2 三个“类似”周一间隔特性分析

选取6月18日、7月16日和8月13日3 d的数据，依据管制员排班情况，这3 d均为同一班组管制员值班，将3 d的管制间隔使用比例数据构成矩阵P3=[p1,p4,p9]，则可得相关系数矩阵：

(7)

相似性计算结果见表5。对应三个类似周一的管制间隔使用比例情况如图7所示。

表5 三个“类似”周一相似性分析Table 5 Three “similar” Mondays’ similarity analysis

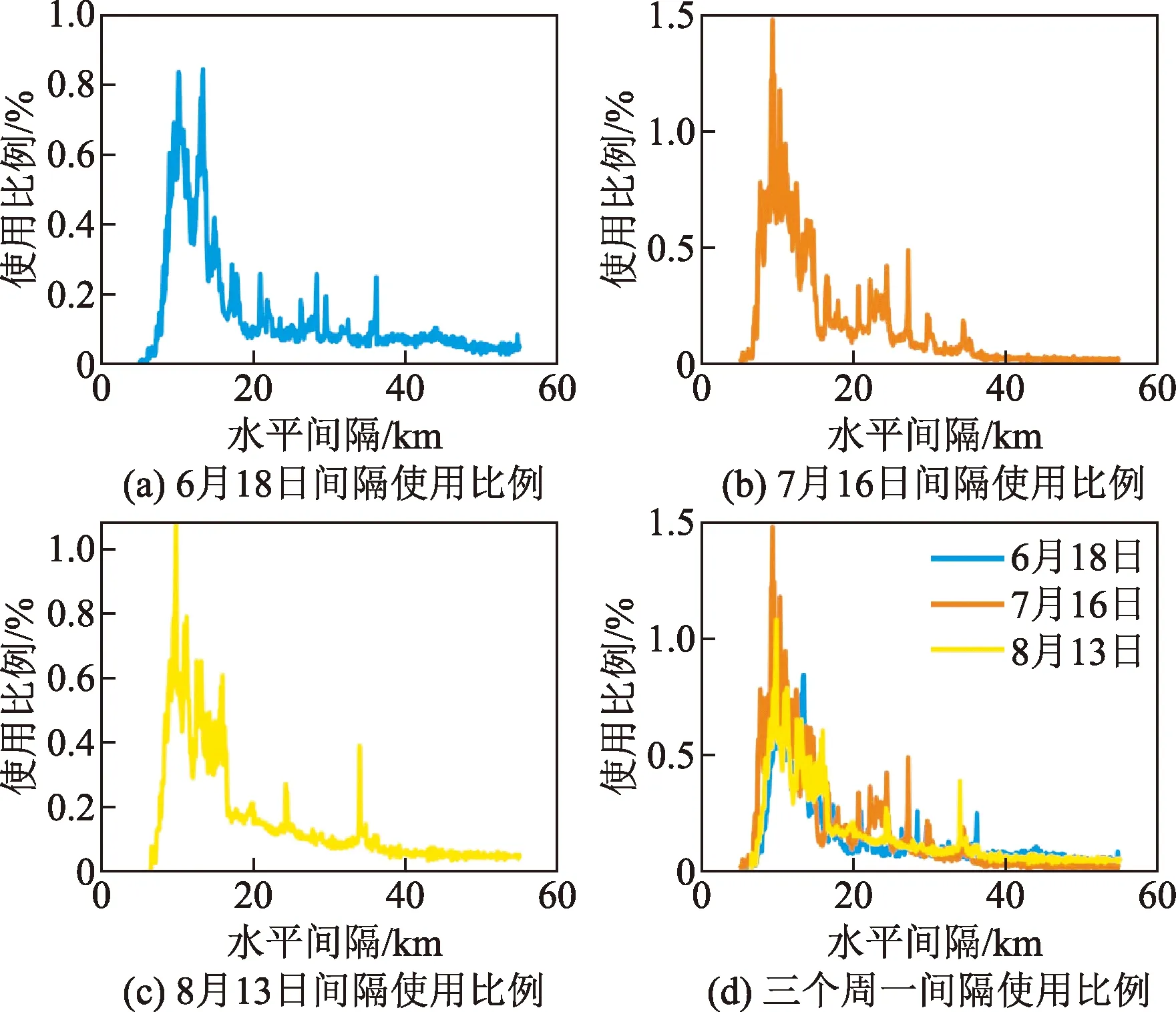
图7 三个类似周一的管制间隔使用比例图Fig.7 Three similar Mondays’ control separation usage proportion chart

由表5计算结果可以看出，三个周一航班架次波动系数较小，其航班运行情况基本一致。分析相似系数可以得出，同一班组管制员值班时，任意两个周一管制间隔的使用都具有较高的相似性。观察这三个周一的管制间隔使用比例图，可以发现每天曲线变化趋势较一致，绘制在同一坐标系中除在水平间隔值为20～35 km区间时重合度较低，但整体而言这3 d的曲线重合度较高，表明管制间隔的使用相似性也较高。

4 结论

在对终端区航空器实际运行轨迹数据处理的基础上，计算航空器对的间隔并计算间隔使用比例，利用相似系数及波动系数分析管制运行间隔的相似性。经过研究分析可以认为，在包括平均航班架次、航班构成和天气情况等在内的管制环境大体一致的“类似”日中，管制员使用管制间隔时具有一定的相似性，尤其对于同一班组管制员来说，在管制间隔的使用上相似性更高；对于情况接近的“类似”日或连续日来说，不同班组管制员值班时，其管制间隔的运用习惯不尽相同，有一定的差异性，体现在数据中为其管制间隔使用的相似性相较同一班组而言较小。对这种关于运行间隔相似性等类似的问题进行深入研究可以发现管制员在工作方法和管制技巧上的差异，从而分出工作水平的高低，通过鼓励推广高水平工作模式，努力改进低水平工作模式，进而消除这类差异，使得管制员的工作水平在保证安全的前提下，达到高水平的一致，大幅提高管制效率；将这种高水平工作模式进行提炼总结，编成可由计算机执行的命令、程序或者控制律，将可能对未来空中交通管制人工智能的发展提供一定的帮助。