变截面连续箱梁剪力滞效应及其形成机制
2020-06-29刘青林
刘青林
(中国铁建投资集团有限公司 北京 100855)
1 引言
箱梁的剪力滞是翼板纵向弯曲正应力沿横截面不均匀分布的现象,基于平截面假定的杆系有限元分析无法考虑这种弯曲应力的不均匀分布,从而导致应力计算结果可能偏小,因此箱梁剪力滞效应的分析和计算方法早已成为桥梁设计理论中重要研究内容之一。经过多年的研究,国内外专家学者对箱梁剪力滞的计算方法及其效应已达成诸多共识,翼板剪力滞的翘曲纵向位移可以使用二次或者三次抛物线近似描述,由此建立的剪力滞能量变分法和包含翘曲自由度的7自由度梁单元也成为剪力滞分析的主要方法和工具[1-4];比拟杆法利用比拟杆和比拟薄板的平衡条件和位移协调条件建立微分方程,是箱梁剪力滞理论分析的主要方法之一[5-6]。赵志峰[7]等推导了单箱三室箱梁的比拟杆面积计算公式和剪力滞效应计算的控制方程,通过与有机玻璃模型试验结果的对比,验证了比拟杆法分析单箱三室箱梁剪力滞效应的合理性。张元海[8-9]等通过分析箱梁截面剪力流分布规律,提出了翼板纵向位移的计算公式,认为翼板剪力滞翘曲位移模式可以近似使用二次抛物线描述。肖军[10]等基于能量变分原理推导并提出了一种针对不同余弦剪力分布的剪力滞翘曲函数,并以矩形简支箱梁和悬臂箱梁为例,证明了其提出的方法能更好地适应不同荷载作用形式下的箱梁剪力滞效应的求解。杨绿峰[11]等针对传统的一维离散有限元法在分析箱梁剪力滞效应方面的局限性,提出了以箱梁挠度、附加挠度及一阶导数作为单元节点位移参数的一维离散元法,通过与模型试验解以及空间有限元数值解的对比,验证了其提出方法的合理性。马驰[12]等基于能量变分原理推导了波形钢腹板组合箱梁的解析解,计算结果与实测结果吻合较好。周世军[13]等针对传统有限梁单元法无法求解集中弯矩作用下箱梁剪力滞效应,基于能量变分原理构造了一种具有新位移模式的有限梁单元,并通过与变分法解析结果的对比,验证了所提方法的可靠性。
能量变分法和比拟杆法在计算等截面箱梁剪力滞效应方面已有较多的研究成果,但变截面连续箱梁剪力滞效应的理论分析成果相对较少[14],且规范中仅给出了等截面简支梁、悬臂梁、连续梁翼板有效分布宽度取值,并未考虑截面变化对翼板有效分布宽度的影响。目前针对比拟杆的研究多以等截面简支梁和悬臂梁展开,本文以变截面连续箱梁为研究对象,提出了变截面连续梁边界条件的比拟杆处理方法,分析了连续梁正、负剪力滞分布规律及梁高变化对连续梁剪力滞效应的影响,加深了对变截面连续箱梁剪力滞效应的认识和理解。
2 变截面连续箱梁剪力滞效应的比拟杆法控制方程
比拟杆法将箱梁等效为承受轴力的比拟杆和承受面内剪力的比拟薄板组成的结构,每根比拟杆上轴力与两侧薄板内剪力的平衡关系满足式(1)所示的平衡方程,比拟杆和两侧薄板的位移协调条件满足式(2)所示的协调方程。

式中,下标i表示第i根比拟杆,当i-1=0时与之相关的变量即为0;x表示桥跨位置坐标;G为剪切模量,Ni(x)、Ai(x)表示第i根比拟杆的轴力、等效面积,te(x)表示比拟薄板等效厚度,di,i-1表示顶板第i、i-1 根比拟杆之间水平距离;qi,i-1(x)表示第i、i-1根比拟杆之间薄板的剪力流和剪应变,qEi(x)表示箱梁腹板内剪力流,E为弹性模量。
对于等截面箱梁,式(2)中Ai(x)、te(x)沿跨长x不变,对式(2)两边求导后即可得到关于翼板剪力流的二阶微分方程组,箱梁剪力滞效应的求解即转化为翼板剪力流二阶微分方程的求解。但是对于变截面箱梁而言,比拟杆等效面积将沿桥梁轴向发生变化,对式(2)两边求导时会产生Ai(x)、te(x)的导数,产生新的未知数,造成求解困难。为此本文参考文献[15]的处理方法,直接将公式(1)、(2)联立组成关于比拟杆轴力和翼板剪力流的一阶微分方程组并直接求解。需要注意的是变截面箱梁内的竖向弯矩会产生附加剪应力,在求解腹板内剪力流qEi(x)必须考虑该部分附加剪应力[15]。
3 比拟杆法分析变截面箱梁剪力滞效应的合理性验证
参考变截面连续箱梁桥常用的构造尺寸,设计一座桥跨布置为36 m+60 m+36 m的三跨变截面连续箱梁桥(见图1),梁宽25 m,梁高变化采用2次抛物线,墩顶5.0 m,跨中2.0 m,横截面尺寸如图2所示。梁体选用C50混凝土,建立实体有限元模型,支点处设置线约束,跨中截面采用对称边界。为保证求解精度,模型划分为六面体映射网格,截面有限元网格划分如图3所示。

图1 数值算例半桥跨径布置及各截面位置(单位:cm)

图2 数值算例横断面(单位:cm)
图4给出了自重作用下三跨变截面连续梁桥不同桥跨位置处箱梁顶缘的弯曲正应力分布,从图中可以看出本文理论解与实体有限元数值解吻合良好,证实了本文比拟杆算法在计算变截面连续梁桥剪力滞效应的可靠性。具体而言,连续梁中支点负弯矩区的D-D截面呈现正的剪力滞效应,C-C、E-E截面呈现负的剪力滞现象,靠近边支点处的A-A、B-B截面和中跨的大部分区域均呈现正的剪力滞效应,这种现象与简支梁、悬臂梁的剪力滞效应有所不同,这可能是由于翼缘板内水平剪切应力不均匀分布和剪应力方向的变化导致的。

图3 箱梁截面有限元网格划分
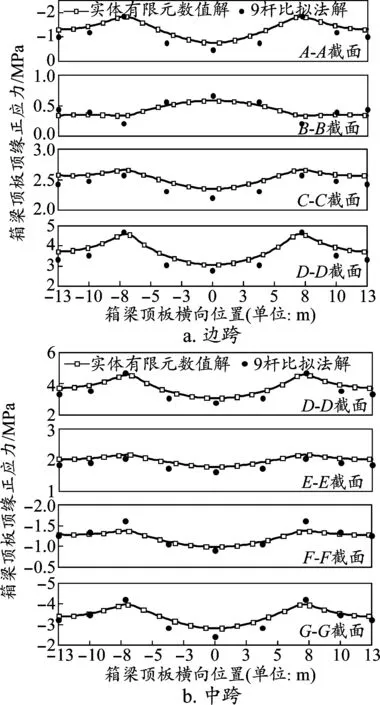
图4 自重作用下数值算例不同位置处顶板顶缘应力分布对比
4 箱梁梁高变化对剪力滞系数的影响
为了进一步分析梁高变化对连续梁剪力滞系数的影响,以上述变截面连续梁算例为参考,设置梁高沿跨径方向2次抛物线变化、1.5次抛物线变化、等高度2 m、等高度5.0 m等4种截面形式,对比4种工况下连续梁剪力滞系数沿跨径方向的变化规律。
图5中给出了4种工况下连续梁剪力滞系数沿跨径方向的分布,从图中可以发现,4种工况下的剪力滞系数的分布规律大致相同,在正弯矩区具有简支梁剪力滞效应的分布特点,负弯矩区具有悬臂梁剪力滞效应的特点,即靠近约束端(中间支点)呈现正剪力滞现象,远离约束端(中间支座)出现负剪力滞现象;连续梁正、负剪力滞交界位置大致在反弯点附近,这可能是由于反弯点附近自重弯矩及弯曲应力均接近于零所造成的;相比中跨而言,边跨的正剪力滞效应更为显著,但负剪力滞区段更短;箱梁截面沿桥跨方向的改变增大了正弯矩区内的剪力滞效应,而减小了负弯矩区内的剪力滞效应,另外连续箱梁梁高变化会增大梁体负剪力滞区长度,并减小正剪力滞区长度;相比于梁高的1.5次抛物线变化,梁高2次抛物线变化时连续梁桥正弯矩区剪力滞系数略大,而负弯矩区剪力滞系数略小。
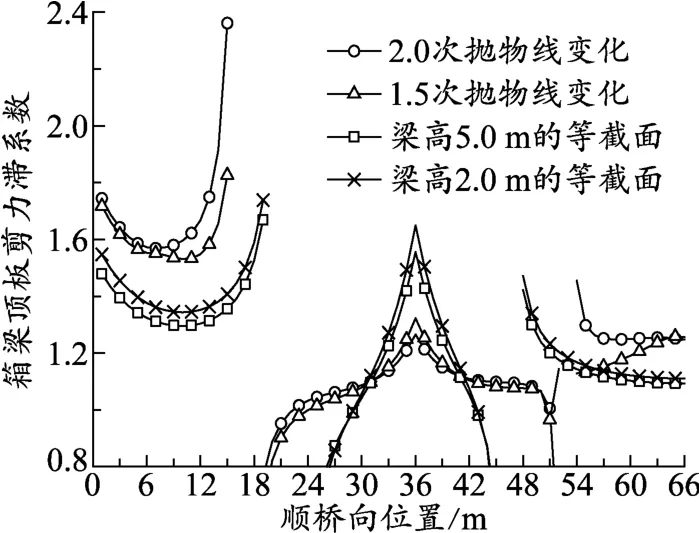
图5 梁高变化对顶板顶缘剪力滞系数的影响
为分析和解释上述现象产生的原因,图6、图7分别给出了4种截面高度变化形式下箱梁腹板剪力流qE和比拟薄板内水平剪力流q21沿桥跨方向的变化情况。从图6中可以看出:连续梁在靠近中间支座处,梁高变化对腹板剪力流的影响与悬臂梁相似[15],梁高从跨中向支点高次抛物线增大的趋势与截面剪力的变化相同,减弱了箱梁腹板剪力流qE沿桥跨方向的变化梯度,且qE量值也有所减小;相反连续梁正弯矩区内梁高的高次抛物线变化反而增大了qE,这表明连续箱梁腹板内的剪力流水平及其沿桥跨方向的变化梯度可能是导致箱梁剪力滞效应的重要外因。从图7中可以看出:中间支点截面附近的负弯矩区内,连续梁梁高的抛物线变化降低了比拟薄板内水平剪力流q21的变化梯度和幅值,而正弯矩区内连续梁梁高的抛物线变化却增大了比拟薄板内水平剪力流的变化梯度,这表明连续箱梁顶板内水平剪力流沿桥跨方向的变化梯度可能是影响连续梁剪力滞效应的主要内因。因此如何在构造上减小连续箱梁腹板和顶板内剪力流沿桥跨方向的变化梯度,尽量让剪力和截面的变化趋势一致可以减小剪力流的变化梯度,进而降低连续箱梁的剪力滞效应。

图6 不同梁高变化形式下qE沿桥跨方向的分布

图7 不同梁高变化形式下比拟薄板内q21沿桥跨方向分布
5 结论
(1)本文提出的变截面连续梁剪力滞效应分析的比拟杆法能正确地计算出各控制截面的剪力滞系数;
(2)连续梁正弯矩区呈现正剪力滞效应,负弯矩区的剪力滞现象与悬臂梁类似,即靠近中间支点处为正剪力滞区段,远离中间支座处呈现负的剪力滞现象;梁高的抛物线变化会减弱连续梁负弯矩区内的剪力滞效应,但会加大连续梁正弯矩区内的剪力滞效应;
(3)工程设计时可以增大连续梁在负弯矩区梁高的变化梯度,并减小正弯矩区内梁高的变化梯度,以最大程度地减小连续箱梁的剪力滞效应。
