规则波中无人艇回收的水动力性能分析

冯大奎，占进*，严军，孙月，王先洲

1 华中科技大学船舶与海洋工程学院，湖北武汉430074

2 高新船舶与深海开发装备协同创新中心，上海200240

3 船舶与海洋工程水动力湖北省重点实验室，湖北武汉430074

4 中国舰船研究设计中心，湖北武汉430064

0 引 言

舰船上的小艇是舰船作战的重要补充，现存的小艇释放和回收方法有3 种：1）特制的回收装置，比如最常见的吊臂结构；2）垂直投放系统；3）艉滑道式小艇收放系统。其中，第3 种收放方法具有稳定性好和效率高等优点［1-2］。在实际作业中，无人艇执行任务后，会在母船尾流中以不同的方向和速度运动，最终被母船艉部的滑道装置回收。

目前，国际上预报高速艇在波浪中纵向运动的方法基本上有3 种：1）对切片法进行湿表面积变化修正的方法；2）采用Wanger 水动力冲量理论的切片方法；3）最近开始研究的直接求解方法，即CFD 仿真。切片法的核心是平面流动假设，不考虑高速纵向流动引起的动升力（或动力矩）。而高速无人艇在顶浪航行时动升力的影响不可忽略，故前2 种方法不能准确预测高速无人艇在波浪中的运动，CFD 仿真是较优的选择。

对于三维CFD 方法，利用基于雷诺平均的Navier-Stokes 方程对流体域中流体的运动进行离散求解，即可对无人艇的运动进行数值仿真。与此同时，一系列由前人得到的无人艇水动力性能试验数据为CFD 仿真奠定了基础。例如，Clement等［3］对美国62 系列滑行艇进行了静水阻力试验，Fridsma［4］研究了波浪中滑行艇的水动力性能。两者都研究了具有不同横向斜升角和长宽比的滑行艇的水动力性能。

数值波浪水池技术、重叠网格技术和六自由度运动模型是对波浪中无人艇运动进行数值仿真的关键技术。学者们利用这些技术对无人艇水动力性能开展了大量的研究。曹洪建［5］利用商业软件FLUENT 对滑行艇在静水中的直航运动进行了数值模拟，并将结果与试验值比较，验证了利用FLUENT 软件研究滑行艇运动、计算研究阻力性能的可行性。苏玉民等［6］针对波浪中滑行艇水动力性能预报的不足，提出一种基于六自由度运动模型的滑行艇水动力性能预报方法，实现了其在波浪中自由运动的水动力性能预报。董文才等［7］分析了现有滑行艇纵向运动理论预报方法的不足，根据滑行艇的艇型特点以及模型静水阻力试验和规则波、不规则波的试验结果，提出了滑行艇纵向运动的基本假设。

大船尾流对无人艇在波浪中运动的干扰，本质上是多体干扰问题。基于无人艇在规则波中运动的研究，学者们对其在大船尾流中的运动进行了仿真研究。Nam 等［8］提出一种基于三维势流求解器的时域数值方法，研究了运动船只对码头边系泊驳船运动的影响。Kashiwagi 等［9］研究了相邻两个浮体之间的水动力相互作用。Castro 等［10］利用计算流体和多体干扰的求解器进行隐形耦合，研究了母船释放和回收无人潜航器的整个过程。但是，之前的研究多限于两船并行，对于航行器前后航行时两者之间由于流体压力传递而导致的影响研究较少，这是由于之前的海上作业中利用艉滑道装置回收无人艇的应用不够广泛，同时，大小相仿的船只前后航行时，两者之间的影响可忽略。

实际上，在研究母船尾流对小尺度无人艇运动的影响时，CFD 仿真相当重要。小艇在大船尾流中快速运动冲向艉部捕捉装置时，由于运动方向和速度大小的不同，在受到尾流影响时可能会出现倾覆危险。为此，本文拟利用数值波浪水池、重叠网格、六自由度运动等技术研究无人艇在规则波中回收的水动力性能，对无人艇沿大船尾流中心线和偏离尾流中心线这两种运动情况进行CFD 仿真，对比无人艇阻力、侧向力以及纵倾角、横摇角等航行姿态的变化，识别可能发生的倾覆风险，以便对实际作业中无人艇的运动控制提出建议，为后续进一步的研究奠定基础。

1 计算模型

1.1 控制方程和流体体积法

绕船流体的基本控制方程是三维连续方程和动量方程。不可压缩流体的连续性方程为

式中，u，v，w为质点速度U在x，y，z 三个方向的分量。

Navier-Stokes 方程为

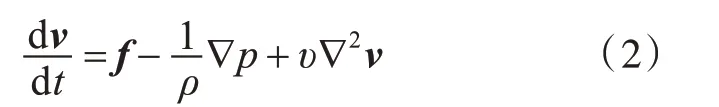
式中：d 为微分符号；v为流体速度；t 为运动时间；f为单位质量流体的体积力；p为流体压力；ρ为流体密度；∇为哈密顿算子；υ为流体的运动粘性系数。

研究中采用的湍流模型是RNG k-e 模型，计算时间步长根据项目验证结果设置为0.005 s。

本文利用流体体积方法来构建和捕捉自由液面。流体体积分数方程F 满足式（3）。

1.2 六自由度运动方程

建立2 个坐标系来确定DTMB 5415 和无人艇的运动，两者均为右手坐标系，一个是固定坐标系（大地坐标系），另一个是运动坐标系，固定在无人艇上，原点保持在无人艇重心G 位置，其中GX，GY，GZ分别表示通过横剖面、纵剖面和水线面的交线，如图1 所示。

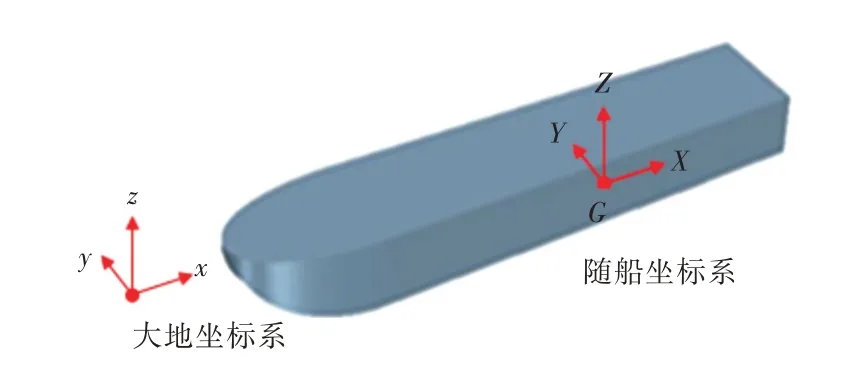
图1 坐标系Fig.1 The coordinates

在大地坐标系中，根据质心运动定理和相对质心的动量矩定理，有

式中：B为无人艇动量；K为其质心相对力矩；F为无人艇受力；M为力矩。

对于运动坐标系，式（4）和式（5）可以写成：

式中，ω为角频率。

式（8）和式（9）即为无人艇的六自由度运动方程：

式中：（FX，FY，FZ）为运动坐标系下无人艇在各个方向上的受力；（L，M，N）为其在运动坐标系下的转矩；m 为无人艇质量；（u，v，w）和（p，q，r）为其在运动坐标系下的线速度和角速度；(IX，IY，IZ)为其在运动坐标系中的惯性矩。

1.3 造波和消波

基于效率考虑，在造波区采用速度边界来造波，其原理是对三维水池做数值仿真，利用UDF函数给出生成边界物体的波浪速度和波高。对于线性规则波，入射边界的速度和波高满足以下条件：

X 方向的速度满足

Y 方向的速度满足

式中：ω为波浪圆频率；A 为波幅；k 为波数；ε为初始相位。

2 数值计算和结果

2.1 几何模型和计算域

无人艇研究对象选择Fridsma 模型，该系列模型构成简单，区别在于具有不同的艇底横向斜升角和长宽比。本文选择的是斜升角为10°、长宽比为5 的无人艇模型。其几何模型如图2 所示。该模型的技术规格如表1 所示。

图2 无人艇几何模型Fig.2 Geometric model of Fridsma hull

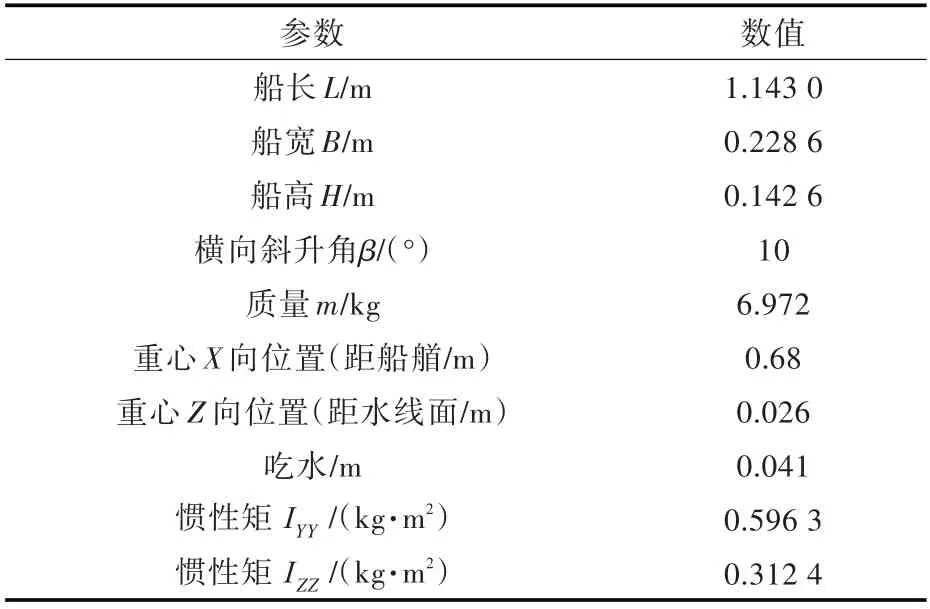
表1 Fridsma 的技术规格Table 1 Specifications of Fridsma

母船研究对象原型选择DTMB 5415。为保证与实际作业下小艇和母船的尺寸一致（母船和无人艇尺寸比在10∶1 左右），对其进行了缩放，缩放后母船的主尺度如表2 所示，其几何模型如图3所示。

对无人艇在规则波中的运动进行仿真时，建立了6.5 m×3 m×3 m 的计算域，即数值波浪水池，其边界条件如图4 所示，只给一个压力出口，其余均设置为速度入口。当计算无人艇在母船尾流中的运动时，需重新建立计算域，但边界条件保持与前者一致。

表2 DTMB 5415 模型的几何参数Table 2 Geometric parameters of DTMB 5415 model

图3 DTMB 5415 几何模型Fig.3 The 3D model of the DTMB 5415

图4 计算域及边界条件Fig.4 Computational domain and boundary conditions

2.2 网格模型

网格划分是整个仿真过程中最关键也最困难的部分，STAR CCM+软件可以进行非结构网格的绘制。绘制网格时，根据流体域的大小和仿真船体的几何尺寸，对整个流体域网格以及小船和DTMB 5415 表面的网格在根据工程项目经验确定基本尺寸后，通过仿真计算进行网格独立性验证，以确定最终网格模型。同时，为了更精细地捕捉自由液面，在水池长度方向单元网格尺寸设置为波长的1/100，波面处单元网格Z 向尺寸设为波高的1/12。由于计算域很大，对船体周围网格的精细程度要求比较高，所以设置了对应的体加密，其余部分网格尺寸可以相对较大，以节省计算资源。将整个控制域分成两个部分，一个是无人艇所在的内部域，一个是外部域，两者进行网格重叠，以达到其运动要求。图5 给出了无人艇在规则波中运动仿真时的局部网格模型，其与模拟无人艇在母船尾流中运动时网格尺寸的设置基本一致。

3 验 证

3.1 数值造波验证

图5 无人艇和自由液面处网格Fig.5 Meshes of USV and free surface

为了分析数值波浪的产生和运动，构建了数值波浪水池。初始自由液面在Z=0.041 m 处，水池深度为HT=2.041 m。具体的波浪参数与Fridsma［4］在1968年试验的波浪保持一致，波长λ=1.714 5 m，波高h=0.050 75 m。设置消波区域，长度为2 倍波长。图6 给出了数值波浪云图。图7 给出了计算波形和理论波形的对比。由图可知，数值计算波形与理论波形基本吻合，满足仿真要求。

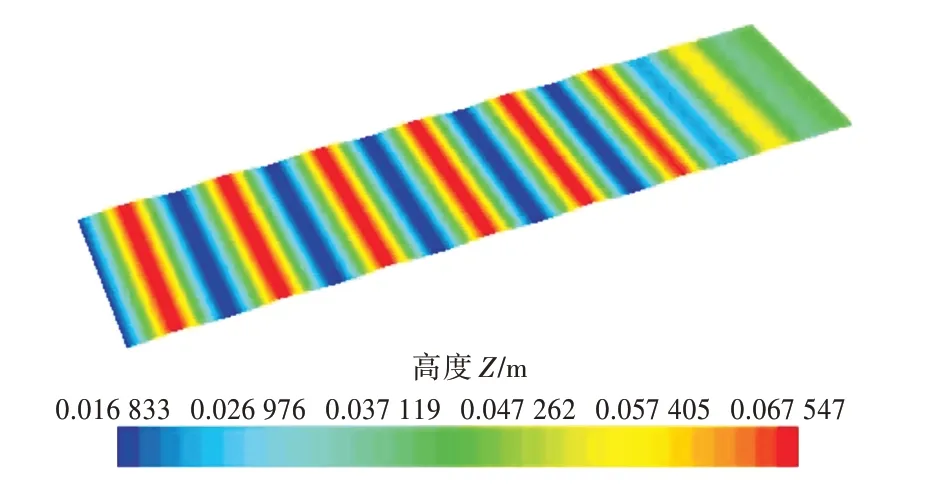
图6 波形云图Fig.6 Contours of wave profile

图7 计算波形与理论波形对比Fig.7 Time histories of computed and theory wave profiles

3.2 网格独立性验证

无人艇航速为2.2 m/s，与试验保持一致，允许其纵倾、升沉以及横摇，监测其波浪阻力以与试验数据对比。为了保证结果的准确性，需进行网格独立性验证，绘制了3 套网格进行仿真。不同网格模型下无人艇波浪阻力平均值及其与试验值的误差如表3 所示。由仿真结果可知，第2 套网格（网格数1 600 万）能在减少计算量的基础上保证计算精度。

图8 是利用第2 套网格进行CFD 仿真得到的规则波中无人艇阻力随时间变化的曲线，其变化趋势符合实际情况，进一步说明了该套网格符合计算要求。

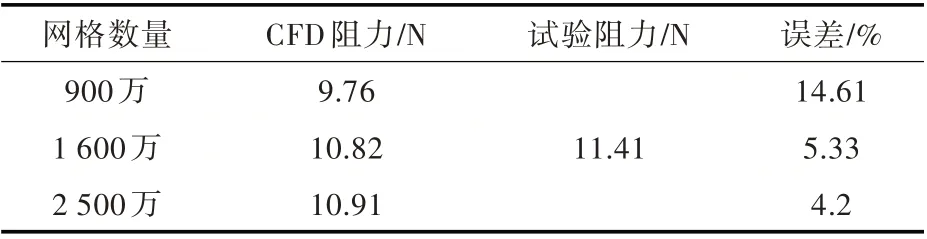
表3 规则波中无人艇的阻力Table 3 Mean resistance of USV in regular waves

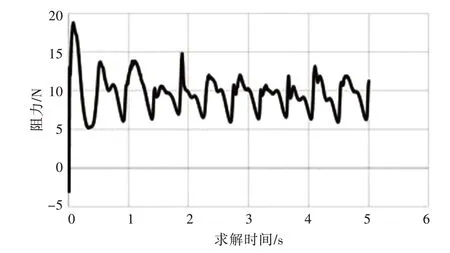
图8 CFD 模拟得到的无人艇阻力变化曲线Fig.8 Resistance of USV by CFD

4 仿真及结果分析

4.1 仿真过程

为研究母船尾流对无人艇运动的影响，本文对两种运动情况进行了数值仿真：一是无人艇沿着母船尾流中心线运动（Δl/L=0，Δl 为无人艇航向距母船尾流中心线距离），二是无人艇运动方向偏离该中心线约一倍船长（Δl/L≈1）。无人艇航速设为4 m/s，母船航速设为2 m/s。仿真中，对于小艇速度运用的是STAR CCM+软件中的平面运动机构功能，这样设置可以使小艇的速度在整个运动过程中保持恒定，不受母船尾流影响。波浪参数与之前保持一致，两船初始间距约9 倍艇长（图9 中用符号D 表示）。无人艇的两种运动情况如图9 所示。

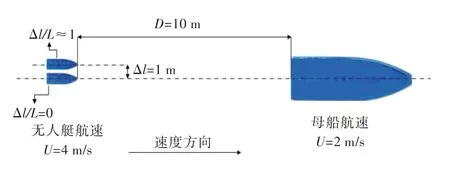
图9 无人艇运动示意图Fig.9 Schematic diagram of motions

4.2 结果分析

对上述两种运动过程进行了4 s 的仿真计算，考虑到实际情况中无人艇过于靠近母船尾部时螺旋桨转动会对其产生较大影响，故在无人艇距母船2 倍艇长时停止仿真。图10～图13 分别给出了两种工况下无人艇阻力、侧向力、纵倾角和横摇角随时间变化的曲线。

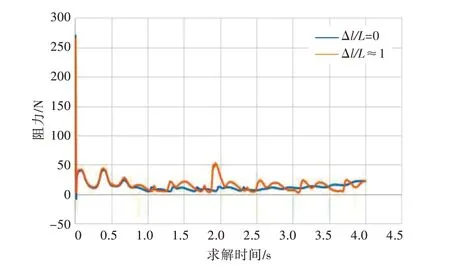
图10 两种情况下无人艇阻力对比曲线Fig.10 Comparison of resistance of USV between two schemes

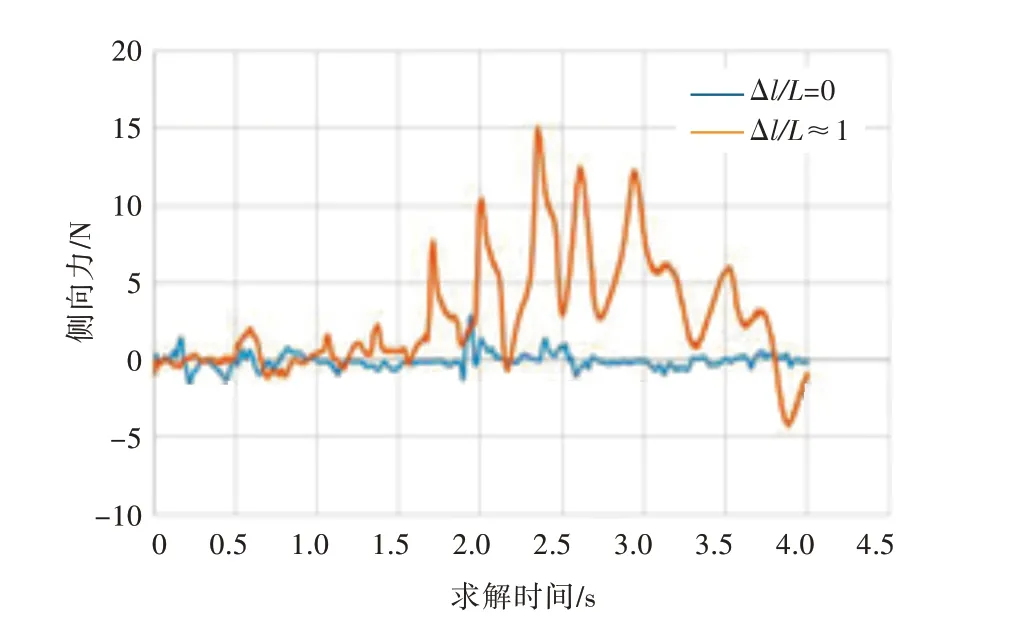
图11 两种情况下无人艇侧向力对比曲线Fig.11 Comparison of lateral force of USV between two schemes

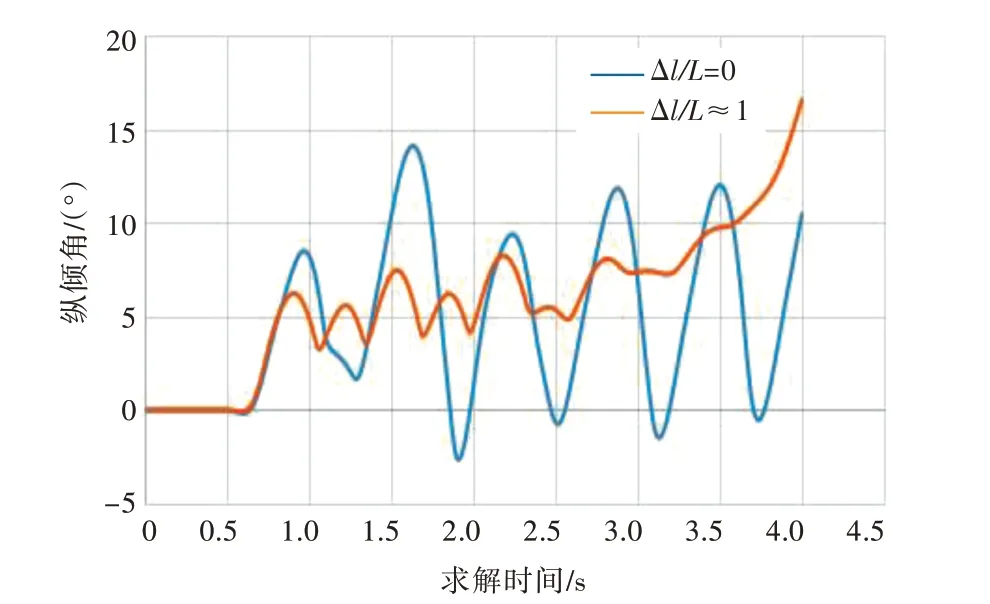
图12 两种情况况下无人艇纵倾角对比曲线Fig.12 Comparison of trim angle of USV between two schemes

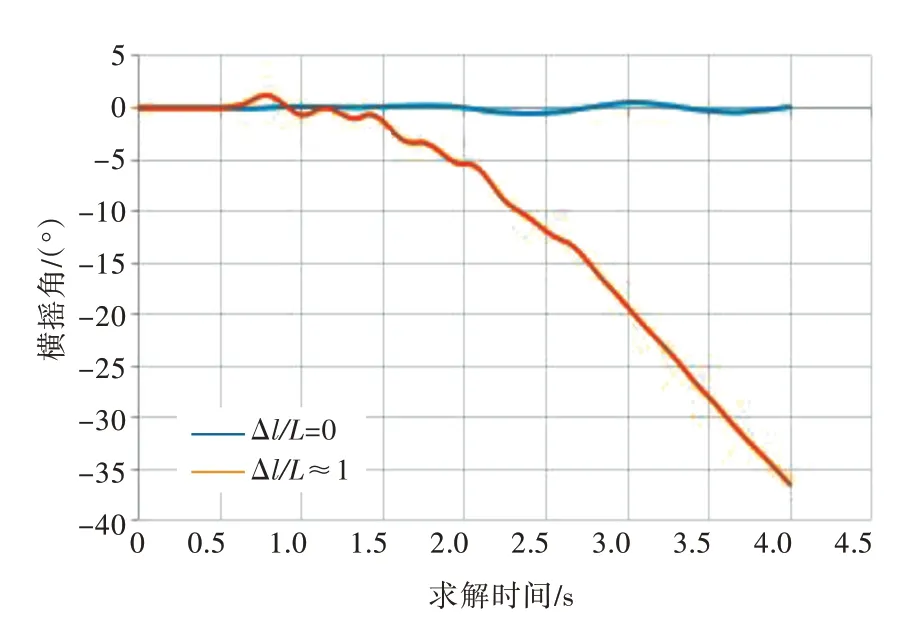
图13 两种请况下无人艇横摇角对比曲线Fig.13 Comparison of roll angle of USV between two schemes

由图10 可以看出，在仿真刚开始进行时，由于无人艇距母船较远，故两种情况下其阻力基本一致。当无人艇逐渐靠近母船时，开始出现差异，在第2 种情况下无人艇由于受尾流影响，其阻力波动更为剧烈，但均值与运动仿真结果基本一致。

由图11 可以看出，两种情况下无人艇的侧向力在仿真刚开始时基本一致，几乎为零。驶近后，母船尾流对无人艇运动的影响开始显现，侧向力开始剧烈变化，这与实际情况相符。

由图12 可以看出：当无人艇沿着尾流中心线由远及近驶向母船时，其纵倾角最后呈规律性变化，航行攻角在5°附近周期性波动；当无人艇运动方向偏离尾流中心线时，由于受尾流影响，其纵倾角不再规律性变化，而是一直增大，仿真停止时其纵倾角达到16°。

由图13 可以看出，两种情况下无人艇的横摇角差别十分明显。当Δl/L=0 时，其横摇角在零轴附近波动，这与实际情况相符。当无人艇运动方向偏离尾流中心线时，其横摇角持续增大，仿真停止时其横摇角近40°，且有继续增大的趋势，这与其侧向力的剧烈变化有关。在这种情况下，无人艇存在倾覆风险，在实际操舵中需要加以避免。同时，由于模拟中限制了无人艇在Y 向的平动和绕Z 轴的转动，也是出现这种极端情况的原因。在实际运动中，会通过操舵调整航向等措施来避免。

图14 给出了3 个时刻自由液面云图的对比，展示了规则波中无人艇在两种运动情况下由远及近驶向母船的过程，揭示了母船兴波对无人艇运动的影响。当运动方向偏离时，无人艇在复杂尾流中纵向运动，因而稳性受到影响。

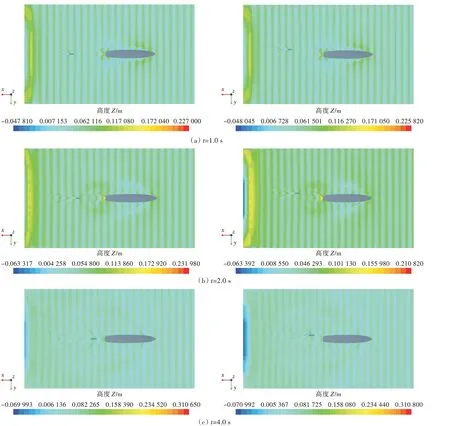
图14 两种情况下不同时刻自由液面云图对比（Δl/L=0 与Δl/L≈1）Fig.14 Contours comparison of the free-surface at different time（Δl/L=0 vs Δl/L≈1）

5 结 语

本文对无人艇在母船尾流中的运动进行了仿真，对比了两种运动下无人艇阻力、侧向力、纵倾角和横摇角随时间变化的曲线，具备一定的现实意义。无人艇与母船距离达到一定值时，其尾流的影响才开始显著，这可以为操舵时机提供参考。当无人艇航向不在母船尾流中心线时（这种情况很常见），母船兴波对其运动，尤其是横向运动与横摇，影响显著。若无人艇在靠近母船时不进行减速或操舵操作，可能会发生倾覆；而当其沿母船尾流中心线运动时，过程更加平稳。该结论可为无人艇回收的行驶路线提供参考。

下一步研究中，将针对无人艇的运动方向和速度进行多组仿真，以便为操舵提供更具体的建议。同时，也将研究母船尾部螺旋桨对无人艇运动的影响。

文中限制了无人艇在Y 方向的平动和绕Z 轴的转动，这也导致其在偏离尾流中心线运动时出现横摇过大的情况，后续将会打开这2 个方向的自由度，为无人艇施加PID 控制，以探寻避免倾覆风险的方法。