基于深度信念网络的船舶柴油机智能故障诊断

仲国强，贾宝柱，肖峰，王怀宇

1 大连海事大学轮机工程学院，辽宁大连116026

2 广东海洋大学海运学院，广东湛江524088

0 引 言

船舶大型中、低速柴油机的运动形式和系统结构较为复杂，部分运动部件的机械负荷和热负荷较高，其中润滑、冷却不良及热应力过大等问题极易引发故障，从而影响柴油机的正常运转，为船舶安全航行带来隐患。目前，船舶柴油机的故障诊断主要依赖于人为经验。然而，随着船舶智能化的发展，基于数据驱动的智能故障诊断方法可在一定程度上避免建立复杂的对象模型或过度依赖专家经验等缺点，所以受到了日益广泛的关注［1-2］。

柴油机智能故障诊断一般采用基于小样本数据训练的思路，故需先通过特征提取算法来获取故障信号特征，然后采用支持向量机（support vector machine，SVM）、BP 神 经 网 络（back propagation neural network，BPNN）、极限学习机（extreme learning machine，ELM）等机器学习方法，建立故障诊断模型。贺立敏等［3］利用随机森林对柴油机的热工参数进行了特征提取，并通过SVM 算法诊断了柴油机的常见故障。Zhang 等［4］利用一种新的时间尺度分解方法提取了振动信号，并采用粒子群优化算法对SVM 参数进行了优化，可用于柴油机故障诊断。Xi 等［5］采用t-SNE 算法对特征信号进行了特征提取和可视化处理，并建立了ELM 分类器，可用于识别船舶柴油机的故障隐患。

然而，在实际工程应用中，基于小样本数据训练的方法无法独立完成深层次的特征提取，一旦训练样本较多或特征较复杂时，将易出现陷入局部最优解、识别精度较低和泛化能力较弱等问题［6］。

深度信念网络（deep belief network，DBN）是深度学习框架下常用的一种概率生成模型，其在大量数据样本下更容易捕捉数据特征，具有较强的自主提取特征能力和较高的目标识别精度。与卷积神经网络算法相比，DBN 具有训练样本量小、操作灵活简单、与其他算法兼容性好等优点［7］。车畅畅等［8］和李本威等［9］采用DBN 对涡扇发动机的状态监测参数进行了处理，诊断了发动机部件的性能衰退故障。贾继德等［10］利用连续小波变换和DBN 对柴油机缸盖振动信号进行了特征提取和模型训练，实现了柴油机的失火故障识别。李军亮等［11］利用DBN 预测了发动机状态参数，可为可靠性分析和预防性维护工作提供数据支持。

通过结合无监督学习和有监督学习的特点，DBN 算法可以从样本数据中自主学习并提取隐性特征，同时获取较优的初始化权值，从而避免浅层神经网络因随机初始化权值而陷入局部最小值和计算精度较低等问题。为此，本文拟提出一种基于深度信念网络的船舶柴油机故障诊断方法，并将开展故障仿真实验，从而评估对比不同算法的计算精度和泛化性能，用以为柴油机智能故障诊断提供参考。

1 深度信念网络的原理

1.1 限制性玻尔兹曼机（RBM）

深度信念网络由多层限制性玻尔兹曼机（restricted Boltzmann machine，RBM）堆叠而成，每层RBM 通过调整神经元之间的权值，即可使整个神经网络按照最大概率来生成训练数据［11］，从而进行特征提取和目标识别。典型的RBM 结构是由1 个可见层v和1 个隐含层h组成的双层网络，如图1 所示。可见层用于接收输入数据，隐含层用于提取数据特征，可见层神经元与隐含层神经元相互连接，而各层内的神经元则相互独立。

图1中：v=[v1，v2，...，vn]，为可见层单元的n个输 入 节 点；h=[h1，h2，...，hm] ，为 隐 含 层 单 元 的m 个输出节点；w=[wij]n×m，为输入层到输出层的连接权值矩阵，其中i=1，2，…，n 且j=1，2，…，m；A=[a1，a2，...，an]，其中ai为第i 个可见单元vi的偏置；B=[b1，b2，...，bm]，其中bj为第j个隐含单元hj的偏置。

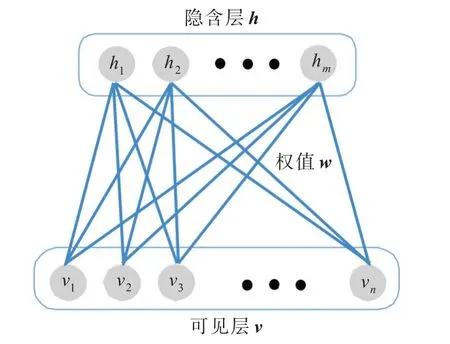
图1 限制性玻尔兹曼机的结构Fig.1 Structure of restricted Boltzmann machine

对于给定的可见层输入v和隐含层输出h，限制性玻尔兹曼机的能量函数E( )

v，h|θ为

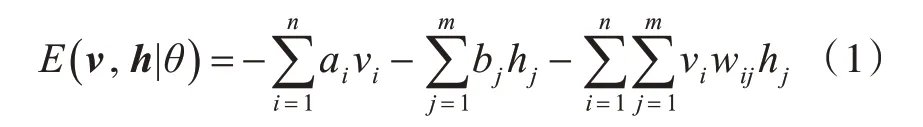
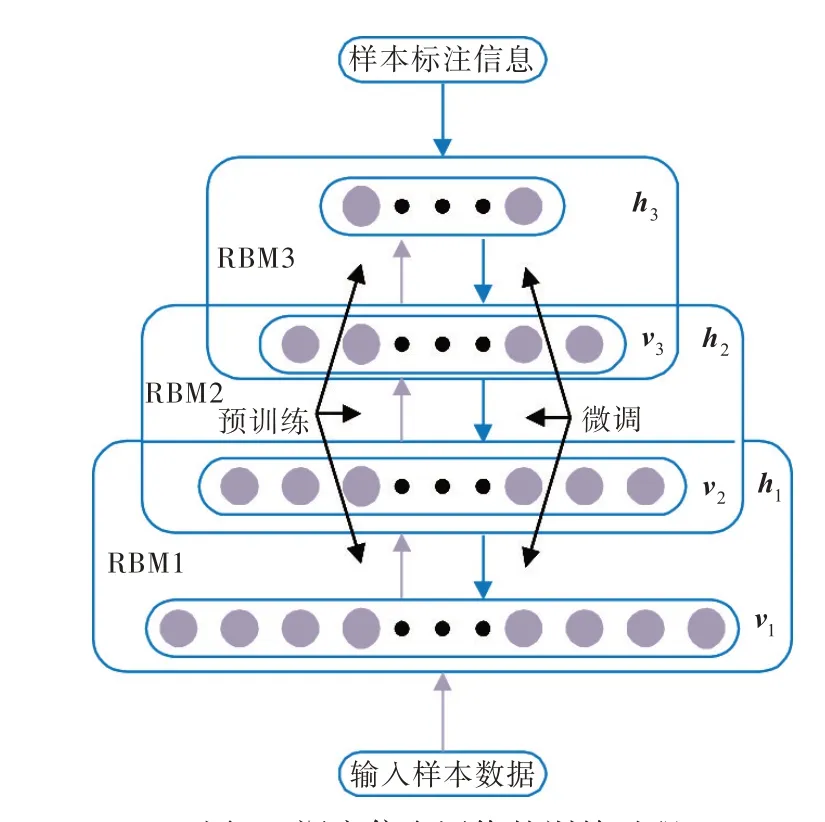
图2 深度信念网络的训练过程Fig.2 The training process of deep belief network

3 故障诊断流程

基于深度信念网络的船舶柴油机故障诊断方法主要包括离线学习和在线识别2 个阶段，具体步骤如图3 所示。

步骤1：故障样本的数据预处理。该项工作包括数据标准化处理和故障类型编码，并划分为训练样本集和测试样本集。

步骤2：创建基于DBN 的故障诊断模型，设置RBM 层数和每层RBM 的节点数。

图3 船舶柴油机的故障诊断流程Fig.3 Fault diagnosis process of marine diesel engine

步骤3：模型预训练。将训练样本集导入模型中，从下而上逐层训练各层RBM，按照式（10）～式（12），获得各层RBM 的初始化参数wij，ai，bj。

步骤4：模型微调。采用BP 神经网络算法反向调整预训练参数，得到最终的DBN 模型。

步骤5：测试柴油机故障诊断模型的性能。将测试样本集传入诊断模型，进行故障预测和实船工况对比，从而评估该故障诊断模型的性能。

步骤6：在线故障识别。将柴油机实时运行数据进行预处理，然后导入故障诊断模型，进行故障识别。

4 实 例

以某型船舶柴油机为研究对象，采用AVL BOOST 软件建立故障仿真模型，并开展故障仿真实验以获取相关的热工性能参数［14-15］。在100%，90%，80%负荷工况下，分别设置单缸供油量不均（d1）、增压器效率低下（d2）、空冷器效率低下（d3）、喷油过晚（d4）、喷油过早（d5）和正常状态（d6）这6种运行状态。同时，设置增压器出口（MP1）、空冷器出口（MP2）、排气总管（MP3）及涡轮出口（MP4）这4 个测量点，并选取各测量点的气体压力、温度和流速以及主机的输出功率P、输出扭矩N、最高爆发压力Pmax等15 个热工性能参数［3，8-10，14-15］。在100%工况下的6 种运行状态原始数据如表1 所示。根据故障仿真实验，可以获得规模为690×15的训练集和规模为360×15 的测试集。训练样本与测试样本是在同等故障模式下的不同样本，训练样本可用于评估其训练效果，测试样本可用于评估模型的泛化能力。

4.1 柴油机故障诊断模型

采用DBN 算法建立柴油机故障诊断模型时，需对网络结构参数进行设定。根据经验，第1 层和最后1 层RBM 的节点数量应与输入数据样本的属性维数和类别数对应。本文将RBM 的初始学习率设为0.01，训练数据批处理量设为50，RBM的激活函数设为sigmoid 函数。为了选取相对较好的网络结构，避免因网络层数过多而导致训练成本较大的问题，通过多次实验，计算不同层数的DBN 平均性能，其对比结果如表2 所示。

重构误差是DBN 在预训练阶段对样本数据进行特征提取的效果评价指标，重构误差越小，表示学习效果越好，其提取特征更具有代表性。从表2 可以看出，随着网络层数增加，耗时随之增加，重构误差逐渐降低到一定程度后略有波动，而网络的准确率先增加后减小，这是由于网络层数增加到一定数值后，复杂网络将出现过拟合的问题。综合考虑重构误差、准确率和耗时3 种性能指标，本文选择3 层RBM 作为DBN，并选择网络节点为15-3-11-9-6 的3 层RBM 进行训练。图4所示为在预训练阶段，3 层RBM 的重构误差随重构次数的变化曲线。由图4 可知，每层RBM 的重构误差均随重构次数的增加而不断减小，其中第3 层RBM 的重构误差在第56 次重构训练时已降至最小值0.244 9。因此，经过3 层RBM 学习之后，即可从原始样本集中提取代表性较强的特征，同时对网络参数进行初始化处理。

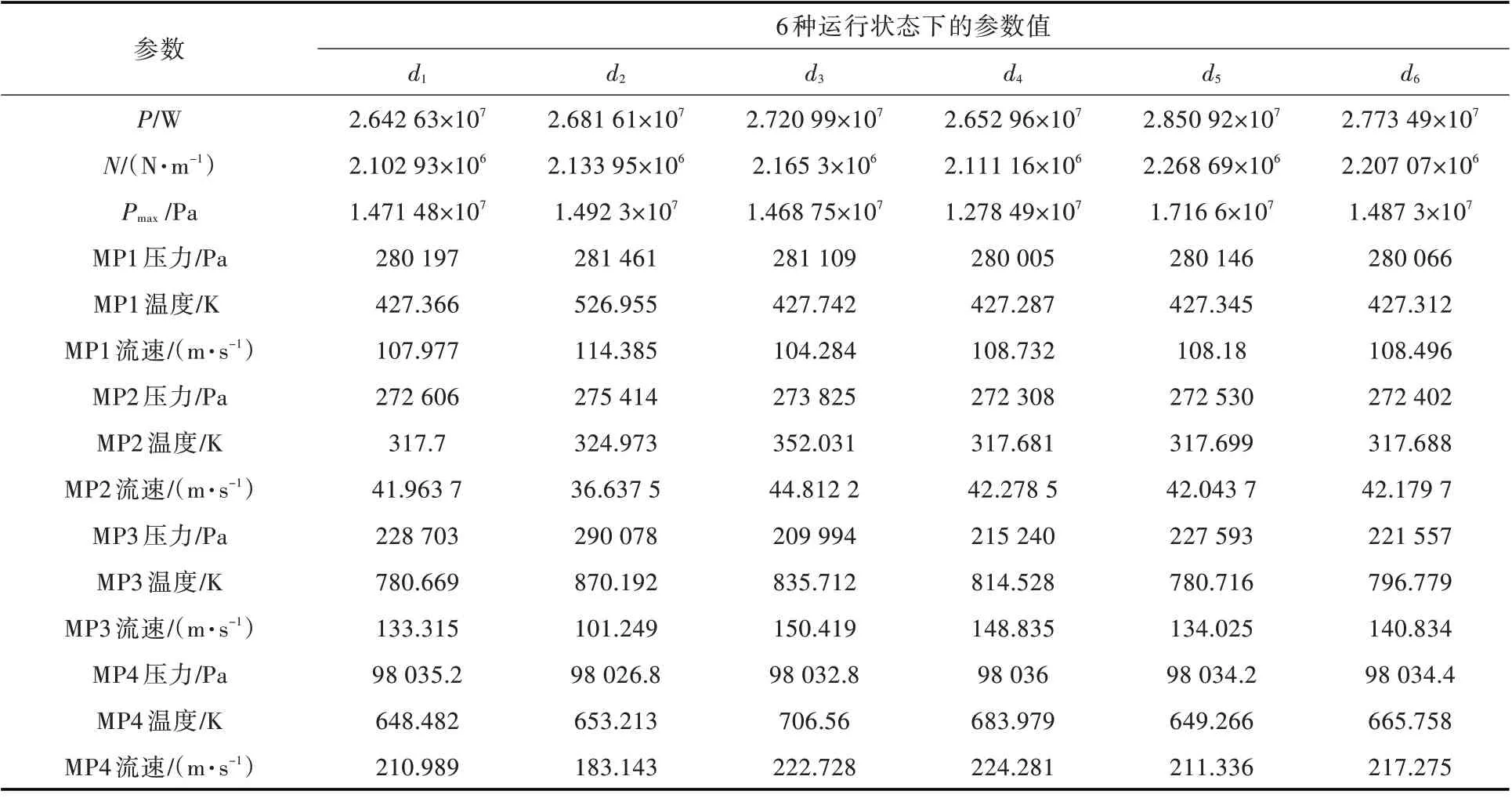
表1 在不同状态下船舶柴油机的原始状态数据Table 1 The original state data of marine diesel engine in different states

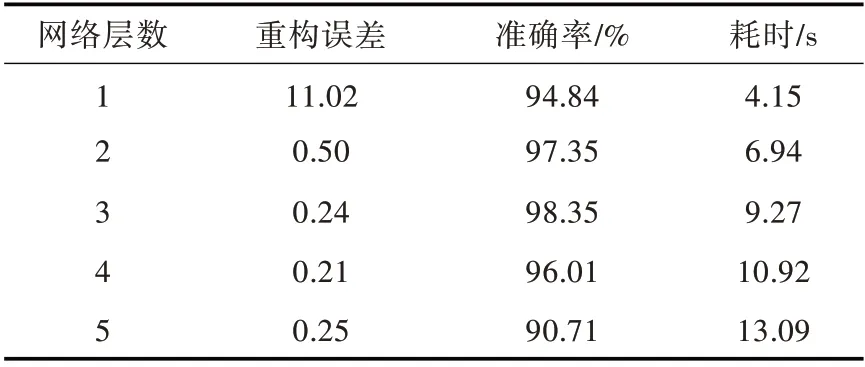
表2 不同结构的DBN 性能对比Table 2 Comparison of DBN performance with different structures

在预训练阶段所提取的特征和初始化参数，将作为下一步微调阶段输入量和网络参数的初始值。在微调阶段，设置BP 神经网络算法的最大训练次数为8 000 次，学习率为0.8。为了考察不同激活函数对训练效果的影响，对不同激活函数softmax，sigmoid，linear 的准确率进行测试，其对比结果如表3 所示。

图4 3 层RBM 的重构误差随重构次数的变化曲线Fig.4 The variation of the reconstruction error of the three-layer RBM with the number of reconstructions

从表3 可以看出，softmax 激活函数的准确率最 高，sigmoid 次 之，linear 最 低，因 此 本 文 选 择softmax 作为DBN 微调阶段的激活函数。在训练过程中，为了防止深度信念网络的过拟合问题，在微调阶段添加了dropout 算法，并将dropout 系数设为0.5。图5 所示为微调阶段DBN 的训练误差。经过训练样本集和测试样本集验证，该DBN 模型的故障识别率分别为98.26%和98.61%。

表3 不同激活函数的准确率Table 3 Accuracy of different activation functions

图5 微调阶段DBN 的训练误差变化曲线Fig.5 Curves of DBN training error in fine tuning

4.2 对比分析

为了进行对比分析，将DBN 算法所采用的数据集分别用于BPNN 和SVM 算法训练。BP 神经网络采用单隐含层，网络节点数为15-13-6，学习率为0.8，最大迭代次数为8 000，训练目标最小误差为0.001，并采用logsig 激活函数和traingdx 训练函数。SVM 算法的惩罚系数C 设为1，核函数选择RBF 函 数。计 算 机 配 置 为：Intel（R）Core（TM）i7-4790 CPU，主 频3.60 GHz，内 存12 G，运 行Matlab 仿真软件。

3 种算法对训练集和测试集样本的训练时间及识别率如表4 所示，可以看出，DBN 算法的耗时最长，但对训练样本集和测试样本集的识别率较高，这反映了该模型的学习训练效果和泛化能力较好。这是因为DBN 具有相对复杂的网络结构，可以从原始训练样本集中提取更深层次的代表性隐含特征，并且在进行BP 神经网络算法训练之前就获取了较好的初始化参数，故其在微调阶段网络训练的效果更好，从而提高了诊断模型的精度。后，可以准确识别的各类别训练样本数量为d1（110/120），d2（120/120），d3（120/120），d4（120/120），d5（120/120），d6（56/90）和d1（110/120），d2（120/120），d3（120/120），d4（120/120），d5（120/120），d6（76/90）。由此可知，3 种算法都可以准确识别运行状态d2～d5的训练样本，但易错误识别d1和d6这2 种状态的样本；其中DBN 算法的识别错误率最低，对故障状态d1和正常状态d6的识别错误分别为4 个和8 个，低于BPNN 和SVM 算法。诊断方法具有较强的泛化能力。

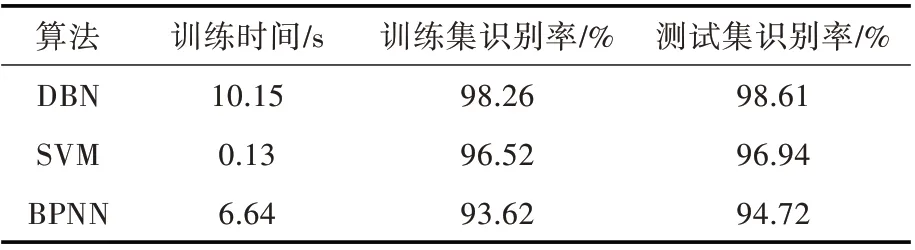
表4 3 种算法故障诊断精度的对比结果Table 4 Comparison of fault diagnosis accuracy of three algorithms

图6 3 种算法对训练样本集识别结果的混淆矩阵Fig.6 Confusion matrix of recognition results of training sample sets by three algorithms

图7 3 种算法对测试样本集识别结果的混淆矩阵Fig.7 Confusion matrix of recognition results of test sample sets by three algorithms

5 结 语

本文将深度信念网络应用于船舶柴油机故障诊断，实现了原始故障样本数据的深层次隐含特征提取和神经网络参数初始化，提升了故障诊断模型的精度和泛化性能。根据某型船用柴油机故障仿真的样本验证结果：基于DBN 的船用柴油机故障诊断方法具有较高的识别精度（高达98.26%）；DBN 算法的故障诊断精度优于BPNN 算法和SVM 算法。需注意的是，与其他机器学习方法类似，DBN 算法也是通过对样本库数据进行学习而成，因此目前无法识别新的故障状态。此外，调整DBN 的网络结构和训练次数时，需要依靠一定程度的人为经验，这有待进一步深入研究。