基于改进AK-MCS 法的船舶板架极限强度可靠性分析

罗文俊，王德禹*

1 上海交通大学海洋工程国家重点实验室，上海200240

2 高新船舶与深海开发装备协同创新中心，上海200240

0 引 言

近年来由于船舶的极限承载能力不够，在高海情下，许多船舶出现了局部失效破损甚至引发整体断裂的海损事故。因此，船舶的极限承载能力是船舶设计中需要重点考虑的方面。目前，国内外学者对于船舶的确定性极限强度的研究颇多，却鲜有考虑诸多不确定因素的船舶极限强度可靠性研究。

蒙特卡罗（MC）法是计算可靠度最准确的方法，且适用于极限状态函数为高维度、多峰、强非线性的情况。结合代理模型采用MC 法计算结构的可靠度，只需知道功能函数值的正负号即可，因此要求代理模型尽可能准确拟合极限状态边界。邱志平等[1]利用人工神经网络构建近似模型获得近似设计点，结合MC 模拟（MCS）计算结构可靠度。Rashki等[2]提出以MC 样本点的概率密度值作为权重因子，筛选出位于失效区域的样本点。张亮等[3]采用神经网络拟合极限状态函数，从而根据函数映射关系生成大量极限状态函数值，然后通过MC 概率分析得到结构的可靠度。陈松坤等[4]以样本点到极限状态边界的距离和权重因子同时作为筛选准则，筛选出极限状态边界附近的点训练BP 模型。Xiao 等[5]开发了3 种学习函数，确保了大多数新选择的训练样本点远离现有样本点，并且使其尽可能接近极限状态函数，在不考虑初始样本不确定性的情况下产生确定的结果。侯国祥等[6]采用神经网络拟合应力函数，结合MCS 计算内燃机的可靠度指标。Lü等[7]提出结合Kriging模型和线性采样的主动学习可靠性分析方法（AK-LS）法，通过构建的主动学习函数H 筛选出对提高Kriging 模型精度最好的样本点，以较少的样本点构造高精度Kriging 模型。Echard 等[8]提出了结合Kriging 模型和MCS 的主动学习可靠性分析方法（AK-MCS），引入了一种学习函数U，通过将失效面附近的点和预测误差较大的点筛选出来，以较少的样本点实现了对极限状态边界的高度拟合。Zheng 等[9]提出 基 于改进AK-MCS 中U 函数的可靠性分析方法，通过采用U 函数筛选出初步最佳样本点，然后再筛选出与初步最佳样本点预测值异号且距离其最近的样本点，通过这两点连线，生成n 个等分点，再通过U 函数筛选出这n+2 点中U 函数值最低的点,作为最佳样本点加入训练集更新Kriging 模型。

AK-LS 方法的优点在于采样点分布在整个设计空间，全局预测精度好；不足之处是Kriging 模型的后期更新效率较低，收敛速度较慢。AK-MCS方法的优点在于采样点主要集中在极限状态边界附近，极限状态边界的拟合精度高，且后期收敛较快；不足之处在于Kriging 模型前期全局拟合精度较低，导致更新效率较低，收敛速度较慢［11］。

本文将充分利用以上两种基于主动学习的可靠性分析方法的优势，采用新的序列采样筛选准则UH，并使用K 折交叉验证（K-fold cross validation）法作为序列采样停止准则，提出改进的AK-MCS 方法，对船舶板架的极限强度可靠性进行研究。使用该方法评估船舶实际航行中局部结构失效破损概率，尤其针对船舶局部较危险结构进行可靠性研究。本文对于船舶板架极限强度可靠性的研究具有重大意义。

1 改进AK-MCS 方法

1.1 学习函数U

在AK-MCS 方法中，Echard 等［8］引入了一种学习函数U：

式中：Ĝ(X)和σĜ(X)分别为Kriging 代理模型预测值的均值和方差。通过计算所有样本点的U 值，将U 值最小点作为下一个最佳样本点加入到实验设计（DOE），同时将Ĝ(X)值接近于0 的点（即失效面附件的点）和σĜ(X)值较大的点（即预测误差较大的点）筛选出来，以更新Kriging 模型。这种方法的优点在于不需要优化算法来识别添加到DOE 的下一个样本点，便于使用Matlab 建模软件中的DACE 工具箱。

1.2 学习函数H

Shannon［10］在1948 年 提 出 了“信 息 熵”的 概念，信息熵是对信息的量化度量。熵随着变量不确定性的增大而增大，分析变量所需的信息量也随之增大。Lü等［7］提出了结合Kriging 模型和线路抽样法（LS）的主动学习可靠性分析（AK-LS）方法，其中引入了基于信息熵的学习函数H：

式中：f(Ĝ(X)) 为Ĝ(X) 的正态分布概率密度函数；H(Ĝ(X)) 为Ĝ(X) 的 混 乱 度，可 以 用 来 判 断Ĝ(X)的不确定性。若某点的信息熵越大，预测越不准确，该样本点对提高代理模型精度的作用越大。

1.3 样本点筛选准则UH

AK-MCS 方法中，样本点筛选准则采用学习函数U，通过计算所有MC 样本点的U 值，选择U值最小点作为最佳样本点，加入DOE中更新Kriging模型。这种筛选准则的缺点是Kriging 模型前期更新效率较低，收敛速度较慢；优点在于采样点集中在失效面附近，可有效提高Kriging 模型对失效面的拟合精度，且后期收敛较快。AK-LS 方法中样本点筛选准则采用学习函数H，通过计算所有MC 样本点的H 值，选择H 值最大点作为最佳样本点，加入DOE 中更新Kriging 模型。这种筛选准则的缺点是Kriging 模型的后期更新效率较低，收敛速度较慢；优点在于采样点分布在整个设计空间，对于前期提高Kriging 模型的全局预测精度贡献较大。

本文采用的筛选准则结合了这两种学习函数的优势。先使用U 函数筛选出少量分布在失效面附近的候选样本点，然后采用H 函数从候选样本点中筛选出对提高Kriging 模型精度贡献最大的点。即结合两种学习函数，在每一轮迭代中筛选出对提高Kriging 模型拟合极限状态边界精度贡献最大的样本点。这种新的筛选准则既能有效保证Kriging 模型的精度，又能提高效率，减少了调用功能函数的次数。

1.4 迭代停止准则

本文迭代停止准则采用K 折交叉验证［5］。将原始DOE 数据均分成K 组，每个子集分别做一次验证集，剩下的K-1 组子集作为训练集，生成K 个代理模型。根据每个代理模型计算失效概率，迭代停止准则为

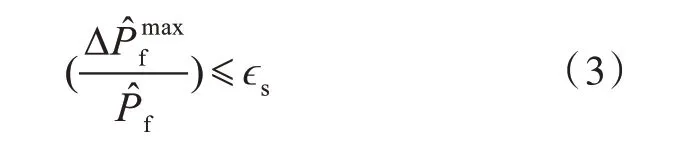
1.5 收敛准则

在MC 方法中，MC 样本容量应足够大才能确保失效概率的准确性。尤其是对于失效概率非常低的情况，需要大量MC 样本点。可根据变异系数评估样本点数量nMC对失效概率计算结果的影响［12］。

每次迭代停止时，需要对输出的变异系数进行校核，以确保样本容量足够大。本文取变异系数C.O.VPf≤0.05。

1.6 改进AK-MCS 方法的计算流程

改进AK-MCS 方法（AK-MCS（UH））的建立具体步骤为：

1）在设计空间中采用MC 采样生成样本集S，所有样本点均不调用有限元模型（FEM）。

2）生成训练集。采用拉丁超立方（LHS）采样生成少量样本点，生成的样本点调用FEM 计算得出响应集，建立初始DOE。

3）根据初始DOE，使用DACE 工具箱建立Kriging 模型。

4）用Kriging 模型预测S 集中样本点的响应值，采用MC 法计算失效概率P̂f。

5）采用样本筛选准则UH筛选出最佳样本点X。

6）开始停止迭代准则判断。若满足停止条件，则进入下一步，否则将样本点X 加入DOE 中，返回步骤3）。重复上述步骤，直到满足停止准则。

7）进行收敛准则判断。检查失效概率的变异系数C.O.VPf，保证该次试验有足够多的样本点。若计算结果低于设定值，则输出失效概率，流程结束；否则生成新的MC 样本点，加入到S 集，返回步骤4），重复上述步骤，直至满足收敛准则。

以上步骤的流程图如图1 所示。

在实际工程应用中，训练集中样本点的响应值往往需要通过耗时的有限元计算得到，训练集过大意味着计算成本巨大。而本文方法致力于以最少的样本点建立具有足够精度的Kriging 模型，从而尽可能减少调用有限元模型的次数，缩减计算成本。

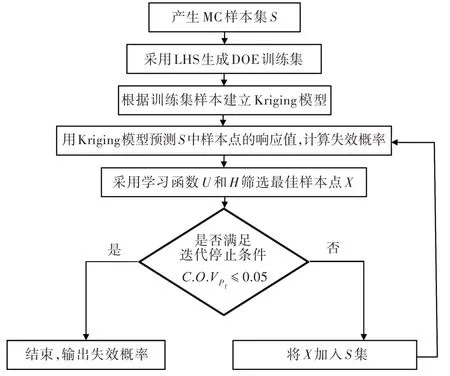
图1 改进AK-MCS 方法流程图Fig.1 Flow chart of improved AK-MCS method

1.7 算例展示

为验证本文提出的改进AK-MCS 方法的有效性和适用性，引用了文献［8］的一个非线性振荡器数学算例，其物理模型如图2（a）所示。采用不同可靠性方法计算对比。该振荡系统的动态响应，如图2 所示。

图2 非线性振荡器Fig.2 Nonlinear oscillator

该模型的功能函数为［8］

献［8］。6 个变量均为各自独立的随机变量，其分布范围如表1 所示。

表1 非线性振荡器设计变量特性Table 1 Nonlinear oscillator design variable characteristics

基于MC 抽样的7×104个样本点，分别运用MC 法、AK-MCS（U）法、AK-MCS（H）法 以 及AK-MCS（UH）法等对样本点进行求解，所得结果如表2 所示。

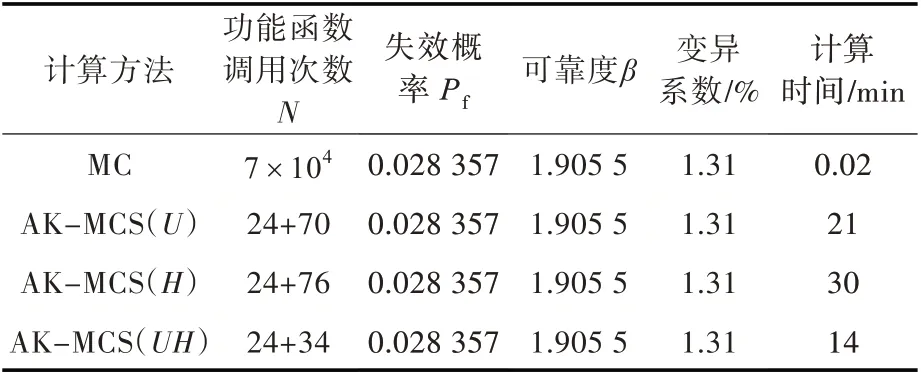
表2 非线性可靠性计算结果Table 2 Nonlinear reliability calculation results

表2 中，功能函数调用次数“24+70”为24 个初始样本点加上70 个筛选样本点。对比结果可以看出：AK-MCS（UH）方法计算的失效概率与MC法的结果一致，说明AK-MCS（UH）方法具有良好的计算精度；AK-MCS（UH）法仅调用了58 次功能函数，比AK-MCS（U）少调用了36次，比AK-MCS（H）少调用了42 次，显著减少了功能函数的调用次数；AK-MCS（UH）的 计 算 时 间 为14 min，比AK-MCS（U），AK-MCS（H）的计算时间各减少了7和16 min，说明AK-MCS（UH）法提高了求解效率。

2 基于改进AK-MCS 法的船舶板架极限强度可靠性分析

由纵骨和横梁组成的板架结构是船舶结构的主要组成部分，因此有必要校核船舶板架的极限强度。在求解船舶板架的极限强度时，材料特性、板厚及载荷等都具有一定的随机性，会对船体板架极限承载能力的计算结果产生影响，因此需要对船舶板架结构极限强度可靠性进行研究。本文将基于改进的AK-MCS 方法对文献中［13］一艘苏伊士型油船的船底板架进行极限强度的可靠性研究，截取船舶中加筋板计算其在组合载荷下的失效概率。几何模型如图3 所示。

图3 加筋板几何示意图Fig.3 Geometric diagram of stiffened plates

加筋板承受中拱弯矩σx，hg作用，底板承受横向水压力P。加筋板模型的功能函数为

G=σU-σx，hg（6）

式中：G＜0 为结构失效；σU为加筋板的极限承载能力，即在横向压力、纵向弯矩组合载荷下的极限强度，调用有限元模型计算；σx，hg为加筋板在中拱状态下的实际承载压力，可根据Shu 等［13］提出的经验公式进行计算。

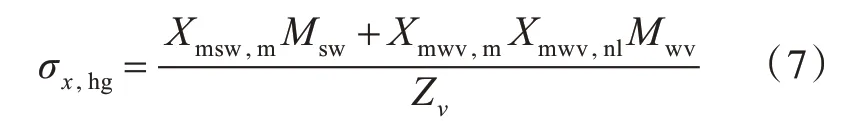
以上各式中参数含义如表3 所示。

表3 加筋板模型参数Table 3 Stiffened plate model parameters

该计算模型选用了纵向双跨距的1/2+1+1/2单根加筋板模型，如图4 所示。本模型同时考虑了几何尺寸与外载荷的不确定性，加筋板模型参数如表3 所示。

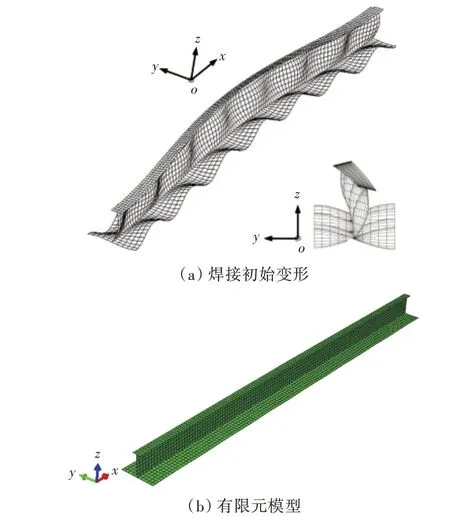
图4 加筋板有限元模型以及焊接初始变形（比例因子为50）Fig.4 Finite element model of stiffened plates and initial deformation of welding（scale factor is 50）

图5 为尺寸取设计值时加筋板在极限状态下的有限元计算结果。

从图5（b），图5（c），图5（d）可知，板架的失效模式分别由梁柱屈曲失效、桁材腹板失效和加筋侧倾失效3 种失效模式耦合组成。

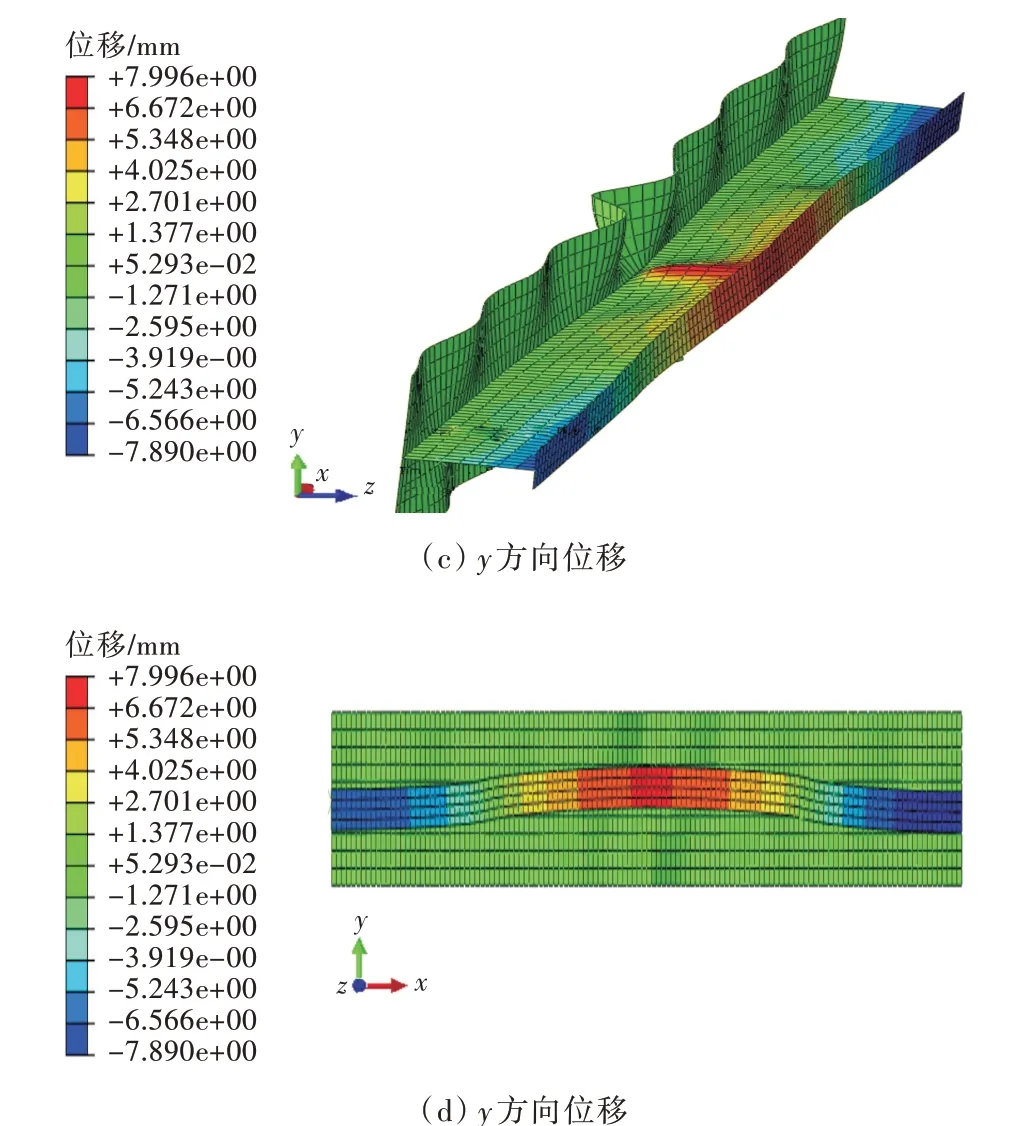
图5 加筋板极限状态下有限元模型计算云图（变形放大倍数为8）Fig.5 The finite element calculation cloud chart of stiffened plate under limit state（deformation magnification is 8）

本算例对比了文献［4］的改进蒙特卡罗法（BP-MC）［4］和文献［13］采用MCS 以及结合二阶响应面的MC 模拟（RS-MC）计算的加筋板的失效概率。同时，采用AK-MCS（U）法，AK-MCS（H）法以及AK-MCS（UH）法对其进行求解，计算结果如表4 所示。

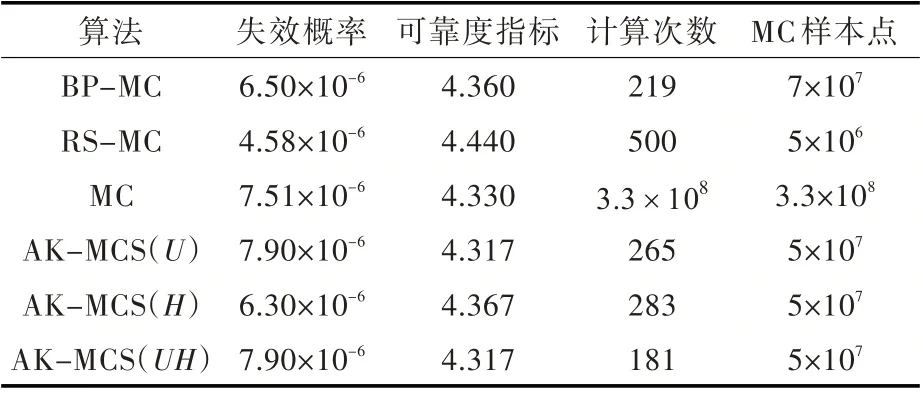
表4 加筋板可靠度计算结果Table 4 Stiffened plate reliability calculation result

由表4可知，改进AK-MCS方法（AK-MCS（UH））计算得到的失效概率最接近MC 方法的计算值，具有较高的计算精度。且仅需调用有限元模型181 次，比AK-MCS（U）法、AK-MCS（H）法 和BP-MC 法各少调用84，102 和38 次，是6 种方法中调用有限元模型次数最少的可靠性方法，有效降低了计算成本，对于船舶板架结构极限强度计算具有较好的适用性。

3 结 论

在工程实际应用中，通常保留了非常大的安全裕度，因此失效概率非常小。在此情况下，难以进行可靠性评估，尤其是当单次有限元模型仿真耗时较长时，计算成本将非常庞大。船舶结构极限强度可靠性分析具备以上特点，为此本文提出了改进AK-MCS 法，并将其应用于组合载荷作用下的船底板架极限强度可靠性分析，得到如下主要结论：

1）改进AK-MCS 法具有较高的求解精度和效率。以非线性振荡器数学模型为例，验证了该方法的可行性。可见，改进AK-MCS 法的计算结果与MC 法结果一致，且显著减少了调用功能函数的次数和计算时间，在保证求解精度的同时提高了计算效率。

2）改进AK-MCS 法在船舶板架极限强度可靠性研究中具有良好的适用性和高效性，与MC法计算结果相比，计算误差只有5%，与文中其他方法相比最接近于MC 法的计算结果，且调用有限元模型次数比原方法减少了32%，有效降低了计算成本。

本文所提改进AK-MCS 方法具有较好的继承性，适用于其他行业的高可靠度工程结构问题，也可以与智能优化算法结合进行可靠性优化设计。