船舶参数横摇数值计算与力学机理分析

朱军，朱韬，王智宇，夏齐强，黄昆仑，葛义军

1 海军工程大学舰船与海洋学院，湖北武汉430033

2 海军研究院特种勤务研究所，上海200235

0 引 言

半个多世纪前，研究人员就注意到，船舶在没有横向作用力的纵向波浪中会发生大幅度的横摇运动，即船舶参数横摇现象。Kerwin［1］采用一阶谐波形式表达了回复力矩的变化量，运用马蒂厄方程构建了横摇运动模型；Paulling 等［2］认为，垂荡和纵摇的非线性耦合至横向会引发横摇运动，其在垂荡或纵摇为谐振运动模式的假定下，导出了一阶谐波回复力矩形式的马蒂厄方程，经模型试验，测定了静水中由垂荡引发的参数横摇运动。

1998 年，巴拿马型C11 大型集装箱船因受极端气象影响而发生了参数横摇运动，导致甲板集装箱遭受巨大损失，再次引起了人们对船舶参数横摇运动的关注。有关船舶参数横摇运动计算，可以归纳为2 类：一是采用马蒂厄方程构建横摇运动模型，其中稳性参数采用遭遇频率的一阶谐波模式；二是采用垂荡、纵摇和横摇的耦合数值计算模型，即直接的摇荡耦合运动数值模拟。

France 等［3］对C11 大型集装箱船遭遇的海况进行了调查，确认了参数横摇发生的海况条件。Shin 等［4-6］针对船舶发生参数横摇运动的现象给出了相同的物理解释，即波浪通过船体时水线面面积会发生周期性的改变，并用遭遇频率的一阶谐波模式描述变化的稳性参数，以垂荡和纵摇的静态或准静态平衡方式估计稳性参数的改变量，以马蒂厄标准方程的数值图解作为稳定性的判据。Belenky 等［5］采用Spyrou［7］给出的参数横摇判别的衡准取决于稳性参数改变量的大小。

在数值计算方面，France 等［3］采用多个耐波性专业软件对参数横摇运动进行了计算，这些软件尽管不是完全针对参数横摇运动开发的，但其计算结果与试验结果在趋势上相同。傅汝德-克雷洛夫波浪力被认为是船舶发生参数横摇运动的关键。Ma 等［8-10］采用瞬时三维压力分布的湿表面积积分计算波浪力，计算研究了船舶的参数横摇运动。鲁江和卜淑霞等［11-12］运用单自由度（类似马蒂厄方程）和三自由度数学模型模拟了参数横摇运动，并在三自由度模型中采用STF 方法处理了波浪力，结果显示，与单自由度模型相比，三自由度模型的效果并非更好。

上述研究均未指明参数横摇运动的能量来源与机制（力学机理），Shin 和Belenky 等［4-5］只是泛泛地认为稳性参数的变化是横摇运动的能量来源，这个机理的认识是数学性的。另外，在国际海事组织（IMO）正在制定的船舶第2 代完整稳性标准中，参数横摇的薄弱性衡准是采用稳性变化量的大小来衡量［6］，然而，不同类型的船舶其计算结果离散较大，这表明以稳性变化量大小作为参数横摇衡准只是权宜办法［5］。

本文拟采用所提出的摇荡耦合切片计算方法［13］，克服大幅运动时参数含义的模糊性，以及会诱发更多自由度运动耦合的缺陷，数值计算船舶的参数横摇运动，由此分析发生参数横摇运动的力学机理，并基于能量原理提出船舶参数横摇的衡准。

1 坐标系及广义参数

1.1 坐标系

3 个坐标系分别为惯性坐标系、船体运动坐标系和船体固定坐标系，如图1 所示。

图1 坐标系Fig.1 Coordinate system

惯性坐标系E-ξηζ的原点E固定于静水面，Eξ轴指向船舶前进方向，Eζ轴垂直向上，Eη轴指向船体右舷。

船体运动坐标系M-xyz在初始时刻与惯性坐标系重合，坐标系沿惯性坐标系的Eξ轴方向以速度U做直线运动。

船体固定坐标系B-xByBzB固定于船体，原点位于船体龙骨基线左右对称面的船舯处，BzB轴线垂直向上，ByB轴线指向船体右舷，BxB轴线指向船艏。

1.2 广义参数

绕船体轴线转动定义的常规横倾角和纵倾角只适合小角度情况，它存在转动顺序问题，即转动顺序不同，船体姿态亦不同。在极端情况，例如当横倾角和纵倾角均为90°时，先后不同地转动横倾角和纵倾角，船体姿态会有很大的差异。为此，本文定义横倾角绕船体纵向坐标轴转动，纵倾角绕静水面横轴线（My 轴）转动，具体定义如下。

假定船舶静水漂浮时吃水为T，船体绕Mx轴线转动横摇角φ，再沿Mz轴平移吃水增量ΔT，最后再绕My轴转动纵倾角θ（图2）。这里，称ΔT，θ分别为广义吃水增量和广义纵倾角。根据转动关系，不难得到船体运动坐标系和船体固定坐标系的转换关系为：

图2 坐标系转动与平移Fig.2 Coordinate systems transformation by rotation and translation

2 船体摇荡耦合运动方程组

习惯上，将运动方程构建在船体固定坐标系中，其优点是绕坐标轴的转动惯量不随运动变化，其为常数，缺点是大幅度运动时易诱发更多自由度的运动耦合。例如，顶浪航行时，垂向波浪力在转换到船体固定坐标系后会有沿船体横向的分量，这个力会导致船体固定坐标下的横荡和摇艏运动。这就意味着原本在静水面观测到的3 个自由度运动，在船体固定坐标下会演变为5 个自由度的运动，这将导致交叉耦合项的水动力出现，使耦合运动的计算变得更加复杂。

因此，本文将摇荡耦合运动方程构建在船体运动坐标的惯性系中。在该惯性坐标系下，随时间不断变化的是船体水下形状，在垂直面内，船体重力和入射波浪力作用会产生垂荡运动，重力和入射波浪力对船舯的力矩会产生纵摇运动。采用普通切片法，将切片的位移、速度和加速度的作用力沿船体纵向积分得到作用于船体的力/力矩，从而不难得到垂荡和纵摇运动方程式为：

式中：ZΔT̈，ZΔṪ，Zθ̈，Zθ̇，ZUθ̇，ZUθ为船体垂荡的水动力系数；Mθ̈，Mθ̇，MΔT̈，MΔṪ，MUθ̇，MUθ为船体纵摇的水动力系数；Fζ和Mζ，Fζ̇和Mζ̇，Fζ̈和Mζ̈分别为入射波浪相对船体位移、速度和加速度的垂向力及纵摇力矩；m为船体质量；Jθ为船体纵向转动惯量；xG为船体重心纵向坐标位置；ρg∇为船体在静水中的排水量，其中ρ为水的密度，g为重力加速度，∇为静水中的排水体积。

横摇运动方程将忽略入射波浪对船体速度和加速度产生的偏心作用，只考虑入射波浪力的位移作用。因此，绕船体重心的横摇运动方程式可写为

式中：ΔIφ和Kφ̇分别为横摇附加惯性矩和阻尼系数；Iφ为船体横向转动惯量；yζ为作用力的横向坐标位置；yG船体重心横向坐标位置。

式（2）和式（3）即构成了船体垂荡、纵摇和横摇的耦合运动方程组。值得注意的是，Fζ是将船体姿态（ΔT，θ，φ）和瞬时波浪位置ζ作为一个整体来计算的，方程组通过力Fζ=f(ΔT，θ，φ，ζ)耦合了船体的垂荡、纵摇和横摇运动，具体计算公式将在后文给出。

3 水动力计算式

3.1 瞬时波面下压力分布

由势流理论，可知船体运动坐标系下小振幅规则波升ζ可表达为

水下压力p的分布式为e 指数形式

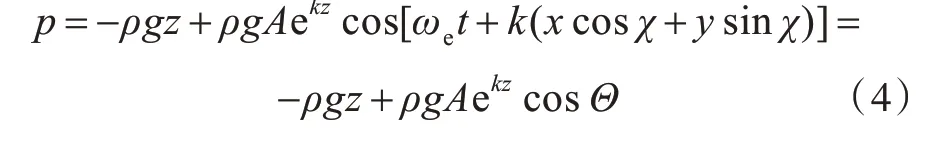
式中：k为波数；χ为浪向角；t 为时间；A 为波幅；ωe为遭遇频率；Θ为计入了时间和位置的波浪相位。为方便起见，令Θ=ωet+k(xcosχ+ysinχ) 。式（4）并不适合直接做压力积分计算，为此，通常采用静水压力和拉伸修正的近似方法［14］，或不做修正。本文采用线性近似，为此，做一个变量代换：

z=z1+AcosΘ

该代换的含义是，z坐标是以静水面为零点，而z1坐标则是以瞬时波面为零点。将其代入式（3），忽略高阶项后，可得压力的近似表达式为

p=-ρ′gz1（5）

式中，ρ′=ρ(1-α0cosΘ) ，为等效水的密度，其中α0=Ak，为最大波倾角。式（4）满足瞬时波面（z1=0）处压力p=0，这就意味着瞬时波面下的压力用等效静水压力近似，等效静水的密度ρ′在波峰区域（cosΘ＞0）较实际水的密度ρ小，在波谷区域（cosΘ＜0）较实际水的密度ρ大。

3.2 入射波浪的位移力

利用高斯定理，将瞬时波面下船体湿表面的压力积分转换成体积分：

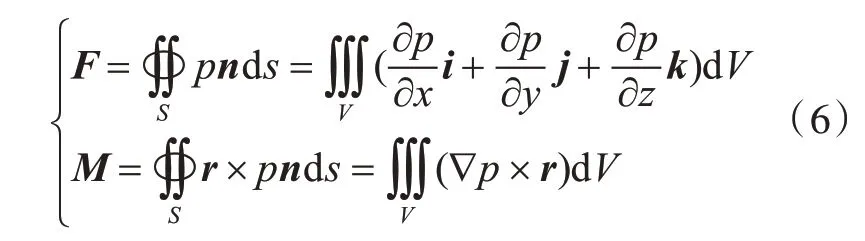
式中，F和M分别为作用于船体的力和绕坐标原点的力矩；s为船体湿表面的面积；V为波浪下船体湿表面的体积；n为船体表面的单位外法向矢量；r为微分湿表面ds到坐标原点的位置矢量；i，j，k分别为船体运动坐标系的3 个单位坐标矢量。将压力的表达式（4）代入到上述力的计算公式中，不难导出瞬时波面下船体入射波浪3 个方向的作用力为：

式中：L 为船长；Sx为瞬时波面下船体切片的面积（图3 中阴影部分面积）。式（7）表明，瞬时波面下船体入射波浪的作用力只有垂向力和纵向力，横向力为0。显然，纵向力Fx与波倾角α0成正比，因波倾角α0为小量，因此纵向力Fx是α0级小量，波浪的主要作用力是垂向力Fz。

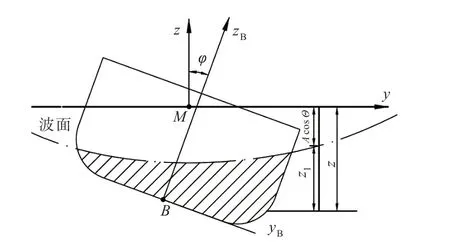
图3 瞬时波面下船体切片示意图Fig.3 Diagram of hull strip under transient wave surface

同样，可以导出绕坐标轴的横摇力矩K 和纵摇力矩M：

式中，xs，ys和zs分别为瞬时波面下船体切片面积中心在船体运动坐标系的坐标值。其中，纵摇力矩M由纵向力和垂向力2 部分构成，也即式（2）中的Mζ。由此，由式（7）和式（8）不难确定出垂向力的横向坐标位置yζ=K/Fz。推导中，利用了顶浪航行条件sinχ=0。

3.3 船体附加质量和阻尼系数估算

式（2）需要计算船体的附加质量和阻尼系数等，本文则将按经验公式来估算。本节中的经验公式和近似图谱来自于文献［15］。

1）船体横摇附加惯性矩和阻尼系数。

船体横摇的惯性矩、附加惯性矩和阻尼系数按照常规单自由度运动方式，以船体平均位置（静水平衡状态）近似估算。横摇附加惯性矩和阻尼系数由经验公式估算：

式中：ρφ为横摇惯性半径，ρφ=CB，其中B为船宽，经验系数C的取值范围为0.33～0.45；2μφ为无量纲横摇衰减系数，其取值范围为0.11～0.14；GM0为初稳性高；Fn 为傅汝德数。

2）切片垂荡附加质量和阻尼。

用二维浮体的宽度、宽吃水比和面积系数这3 个参数来估算船体切片的垂向附加质量和阻尼系数，沿船体纵向积分得出船体的垂荡附加质量、纵摇附加惯性矩和对应的阻尼系数。

二维浮体单位长度的附加质量Δm和阻尼系数ΔNμ估算公式为

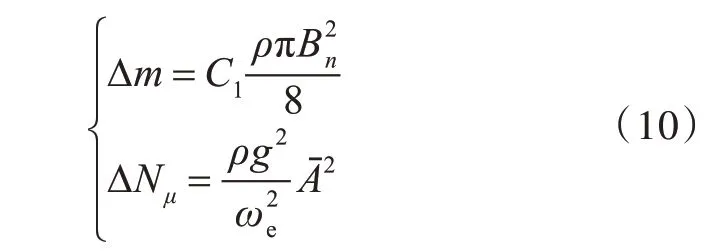
式中：Bn为二维浮体水面处的宽度；C1为附加质量系数；Aˉ为衰减系数，是辐射波幅值与垂荡幅值之比。附加质量系数C1和衰减系数Aˉ的大小与遭遇频率ωe、宽吃水比和水下面积系数有关，本文采用文献［15］的图谱插值近似。

3）船体附加质量和阻尼系数。

对式（2）等号左边的船体垂荡水动力系数和纵摇水动力系数，按照切片在瞬时波面下的船体姿态（ΔT，θ，φ），由式（10）来估算切片附加质量Δm和阻尼系数ΔNμ，然后再沿船体纵向积分得到船体垂荡和纵摇的附加质量及附加惯性矩等。

入射波浪相对于船体速度和加速度的垂向力及纵摇力矩也可按照同样的方法积分计算。

4 参数横摇数值计算及力学机理分析

本文采用上述动力学模型和基于图形面域技术开发的软件计算了一艘船舶在顶浪规则波中的摇荡运动，以此分析船舶发生参数横摇运动的力学机理。

4.1 参数横摇运动计算

计算船舶的船长L=142 m，航速U=14 kn，波陡范围Hw/λ=0.015～0.050。

图4 所示为波陡Hw/λ=0.025 时的垂荡、纵摇和横摇计算时历曲线。计算结果显示：在该状态下呈现出了参数横摇运动，横摇幅值不断增加；同时还表明，横摇频率为纵摇频率的一半，且位于横摇共振频率范围内，这与发生参数横摇的频率条件是吻合的。

图4 顶浪中的摇荡运动计算时历曲线（Hw/λ=0.025）Fig.4 The calculated time history curves of oscillating motions in head wave（Hw/λ=0.025）

表1 参数横摇运动的预报结果Table 1 Prediction results of parametric rolling motion

表1 所示为不同波陡和波长条件下的参数横摇运动预报结果。表中：符号“●”表示横摇运动振荡增加，呈现参数横摇运动；符号“×”表示横摇运动衰减，无参数横摇运动。预报结果显示，除较小的波陡不发生参数横摇运动外，随着波陡的增加，发生参数横摇的波段向高频区偏移，整体上波长/船长（λ/L）在0.9～1.4 范围。

4.2 参数横摇力学机理分析

将式（3）第3 项的回复力矩写成通常的形式：

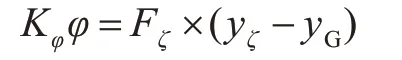
式中，参数Kφ为回复力矩系数，相当于船舶横摇系统刚度，其作用是在每半个横摇周期内，在横摇角增大的过程中吸收能量，在横摇角减小的过程释放所吸收的能量。

图5 回复力矩系数和横摇角计算曲线（λ/L=1.2）Fig.5 calculated curves of recovery moment coefficient and rolling angle（λ/L=1.2）

图6 回复力矩系数和横摇角计算曲线（λ/L=1.5）Fig.6 calculated curve of recovery moment coefficient and rolling angle（λ/L=1.5）

图5 和图6 所示为Hw/λ=0.025 时回复力矩系数Kφ与横摇角φ随时间变化的计算曲线（其中Kφ的单位为N·m，φ的单位为（°），图5、图6 的纵坐标为它们各自乘以不同系数后的尺度）。图5呈现的是参数横摇运动，其λ L=1.2；而图6 呈现的则是横摇运动振荡衰减，其λ L=1.5。从图5 所示的计算曲线可以看出，在横摇角增加过程中，参数Kφ低于平均值，处于较低水平；而在横摇角减小的过程中，参数Kφ高于平均值，处于较高水平。这就意味着在每半个横摇周期内，在横摇角增大过程中所吸收的能量小于横摇角减小过程中释放的能量；图6 的情况与之相反，因而不会出现参数横摇运动。

因此，参数横摇的力学机理是：回复力矩系数Kφ随着波浪的作用呈现出围绕均值的波动，在横摇角减小过程中，其释放的能量要大于横摇角增大过程中回复力矩系数吸收的能量。该能量差值也即参数横摇运动持续放大的能量来源。

4.3 参数横摇衡准

图5 和图6 显示，在不同波长/船长、相同波陡情况下，回复力矩系数Kφ的均值与振荡幅值没有明显差异。如上述分析，是否发生参数横摇运动取决于系统吸收和释放能量的平衡与否，系数Kφ与横摇角φ随时间变化的相对位置，即相位关系决定了吸收与释放能量的相对大小。现用遭遇频率ωe的谐波函数拟合系数Kφ：

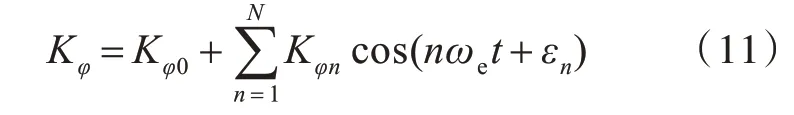
任意一个横摇半周期内，假定横摇角为正弦函数，其频率为用遭遇频率ωe的一半，即

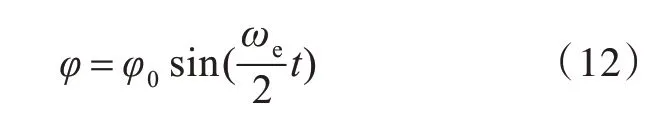
式中，φ0为半周期内的横摇角幅度，为常数。因此不难得到，横摇角半周期内回复力矩系数Kφ吸收和释放的能量总和为

式（13）表明，只有系数Kφ的一阶谐波分量的积分不为0，常数项和高阶谐波项的积分均等于0。发生参数横摇的条件是能量J＜0。因此，满足此条件的相位角ε1可由式（12）得到

这就是参数横摇的判别衡准。

如果将式（11）只保留常数项和一阶谐波项，则与France 等［3-5］研究的参数横摇所采用的马蒂厄方程相类似。但是，判别参数横摇的衡准不同，是否发生参数横摇不取决于一阶谐波项系数的大小，而是一阶谐波项的相位角ε1。相位角ε1的变化取决于船波相对运动，其与波浪中船舶的垂荡、纵摇和由入射波浪引起的水线面形状变化以及水下排水体积变化相关。

5 结 论

本文建立了惯性坐标下的垂荡和纵摇耦合运动方程，以及船体坐标下的横摇运动方程，由此构成垂荡、纵摇和横摇的混合动力学模型，并采用普通切片方法计算了入射波浪力、附加质量和阻尼系数。数值计算了一艘船舶的垂荡、纵摇和横摇耦合运动，预报了参数横摇运动，通过对数值计算结果的分析，得出了参数横摇运动的力学机理和参数横摇判别衡准，研究认为：

1）参数横摇的力学机理是：由于回复力矩系数Kφ是随时间变化的，导致在横摇过程中回复力矩系数吸收和释放的能量不等，释放能量大于吸收能量是发生参数横摇的力学机理，也是发生参数横摇后运动持续放大的能量来源。

2）判别参数横摇的衡准是，回复力矩系数Kφ的一阶谐波分量具有超前的相位角ε1⊂[0，π]。

船舶参数横摇力学机理的明确有助于对参数横摇运动的认识，而如何建立相位角ε1与船体参数的关系尚需深入研究。