基于SEIAQR动力学模型预测湖北省武汉市新型冠状病毒肺炎疫情趋势*

丁中兴 宋文煜 方欣玉 王 凯 鲍倡俊 陈 峰 沈洪兵 武 鸣△ 彭志行△

【提 要】 目的 基于新型冠状病毒传播特点，使用实际数据拟合并预测武汉市疫情发展趋势。方法 考虑新型冠状病毒肺炎传播规律及采取的隔离措施，构建SEIAQR动力学模型；研究使用2020年1月10日至1月31日武汉市累积发病人数及死亡人数数据对模型进行拟合，并使用2月1日至2月10日的实时数据对模型结果进行验证；最后，研究通过模型拟合结果评价现有抗疫防控措施的效果。结果 武汉市发病人数在2月4日左右达到峰值，随后持续下降，2月14日至2月16日出现一个短暂的反弹期，直至5月疫情将基本结束流行。防控措施不变的情况下，疫情结束时预计50780人感染，2449人死亡，粗死亡率约为4.82%；及时有效的防控措施降低了75.08%的感染率和72.40%的因病死亡率；模型拟合偏差约为4.08%。结论 SEIAQR模型拟合效果良好，可以较为准确地预测疾病流行趋势。

21世纪以来全世界共发生三起冠状病毒大流行，分别是2003年严重急性呼吸道综合征(SARS)、2014年中东呼吸综合征(MERS)和2020年新型冠状病毒感染型肺炎(COVID-19)，COVID-19较前两者具有更高的传染性及较低的致死率[1-2]。截至2020年5月1日，中国已报告82875例确诊，77685例治愈和4633例死亡，其中约87.70%(68128例)确诊和97.39%(4512例)死亡来自湖北省[3-4]。1月23日，中国政府启动突发公共卫生事件一级响应，上午10点起武汉的城市公交、地铁、机场和火车站等交通方式暂停运营，1月24日，湖北省启动重大突发公共卫生事件一级响应，陆续封锁其余城市的公共交通。基于传染病动力学模型，本研究拟合并预测武汉市新型冠状病毒肺炎的疫情发展趋势，为科学防控提供参考。

资料与方法

1.数据来源：数据来自于国家卫健委、武汉市卫健委的发布信息，整理得到2020年1月10日至2月10日武汉市新型冠状病毒感染肺炎累积报告病例数、累积治愈病例数及累积死亡病例数，见表1。

2.模型构建：已有学者使用SEIR模型较好地拟合COVID-19流行趋势[5-6]，在此基础上，我们构建SEIAQR模型，总人群N被分为6个仓室：易感者(S)，潜伏者(E)，感染者(I)，无症状感染者(A)，发现并被隔离者(Q)以及康复者(R)；即N=S+E+I+A+Q+R。新冠肺炎的传播流程图如图1所示，因潜伏者和染病者均具有感染性，易感者接触潜伏者或感染者可成为新冠肺炎的病毒携带者，考虑疾病的发生率为标准发生率，易感者与潜伏者或感染者的接触率分别是β(t)，βE(t)，其中β(t)=1-(1-β)C×(1-f(t))×((1-δ)×β)c×f(t)，β表示易感者每次与感染者接触后被感染的平均概率，c表示人群日接触次数，δ表示佩戴各类口罩预防病毒感染的平均有效率，函数f(t)在t时刻时口罩的使用率；βE(t)=εβ(t)，这里ε(0<ε<1)是一个衰减因子，表示潜伏者相对于感染者传染力度的差异；潜伏者以速率k发展成为感染者(其中p部分为有症状感染者，1-p为无症状感染者)；感染者和无症状感染者均以α1的速率恢复，其中感染者因为出现临床症状以速率α2被发现和隔离，因新冠肺炎的病死率为μ。在严格的隔离防控措施下，不考虑隔离者与易感者发生接触，隔离感染者以速率γ恢复。进而建立如下新冠肺炎的动力学模型：

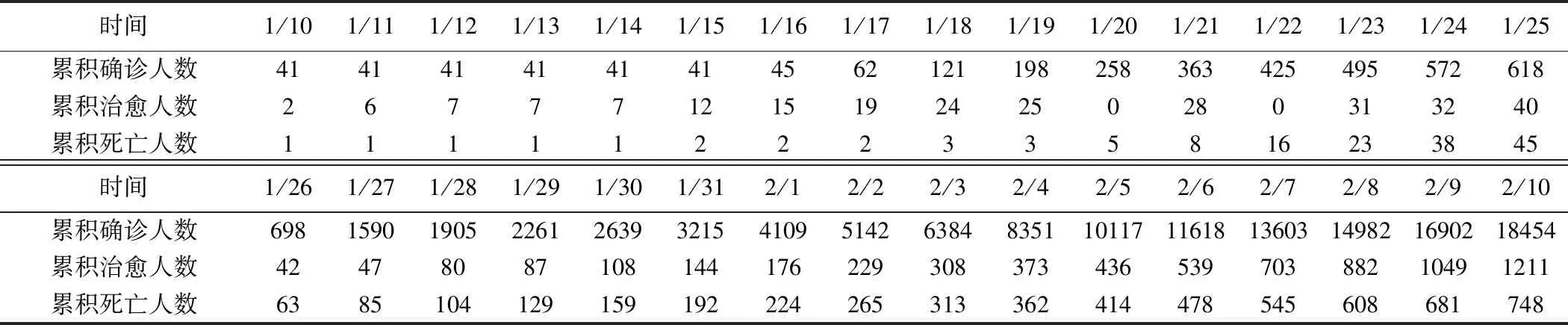
表1 2020年1月10日至1月31日武汉市新型冠状病毒感染肺炎病例

图1 COVID-19传播动力学SEIAQR模型

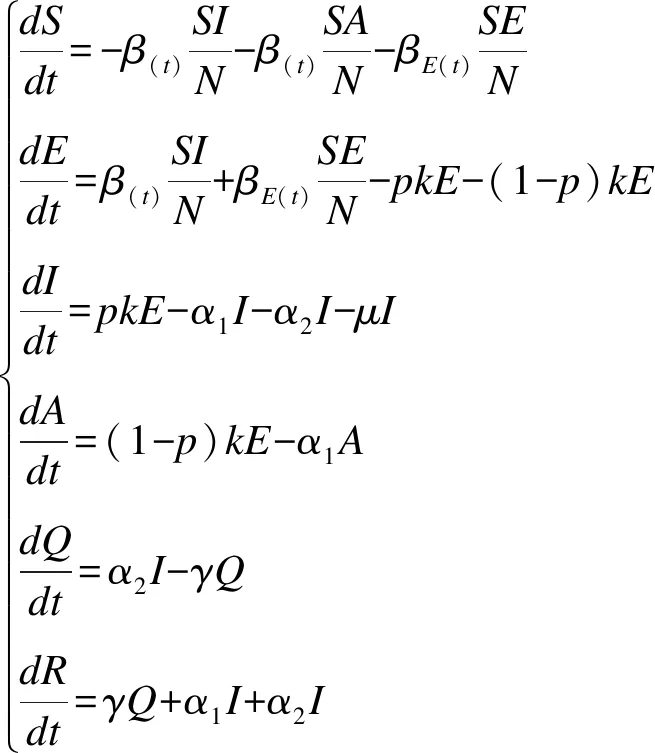
3.参数估计：新型冠状病毒的潜伏期平均为5.2天[5]，发病到隔离、治疗的时间平均为7天[3]，患者住院的中位数为10天[7-9]；人际日接触系数c初始设定为10(1～50)[10]；以既往文献研究为参考，口罩的有效保护率δ设定为0.85(0.8～0.99)[11]。见表2，表3。

表2 SEIAQR模型参数含义及取值

*：专家意见为咨询中华预防医学会新型冠状病毒肺炎防控专家组后得到。

表3 SEIAQR模型仓室含义及初值

本研究从已有数据中截取武汉市1月10日至1月31日的数据进行参数拟合，采用非线性最小二乘的方法拟合潜伏者仓室初始值E(0)，患者自然康复速率α以及传染率系数β。将初步估计出的参数值用作MCMC方法[12]中M-H算法的先验信息，使用Matlab软件进行10000次的迭代，退火后选取后面2000次迭代结果计算各参数平均数及相应95%可信区间。模型预测2月1日后肺炎疫情的流行趋势，通过比较预测结果与2月1日至2月10日实际数据的差异验证参数准确性和合理性。

结 果

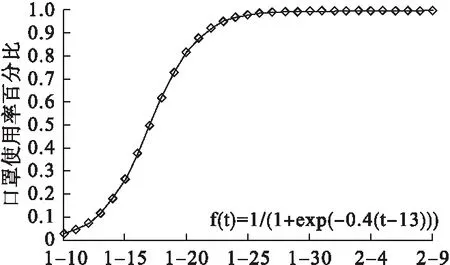
图2 口罩使用率变化趋势图

2.新型冠状病毒肺炎疫情趋势模拟：我们在图3中使用湖北省武汉市1月10日至1月31日累积发病数据及死亡数据对模型参数进行拟合。左上图中data1为实际累积发病者，data2为实际累积死亡者；蓝色实线表示使用模型拟合的累积发病预测值，红色实线表示累积死亡预测值。为了让结果体现更清晰，我们对y轴刻度值取对数后得右上图。结果显示，累积发病数和累积死亡数将在3月1日(第50天)趋于稳定。随着疫情逐渐被控制、消灭，疫情流行结束时预计武汉市会有50780人感染，累积死亡2449人，因病死亡率约为4.82%。使用均方误差(MSE)函数评估模型拟合优度，经计算2月1日至2月10日累积确诊病例数的平均偏差值为4.08%，差异处于可接受范围内，随着日期延长，差异逐渐变小且稳定，故认为本模型中所估计的各参数值较为合理。模型拟合效果见表4。

表4 SEIAQR动力学模型拟合效果评价

图3下行两图显示，模型预测武汉市发病人数在2月4日(第24天)左右达到峰值，预计当天确诊1512人，随后出现一个短暂下降趋势，这个过程持续6～7天。2月14日-2月16日(第34天～37天)疫情可能出现一个反弹期，2月16日(第37天)后持续下降，直至今年5月(第120天)将基本得到控制。随着时间推移，人群防控意识日益淡薄，疫情持续减弱过程中可能出现小幅度回升，但衰减趋势保持不变。实际数据显示，2月4日附近出现峰值，当天共有1967人次确诊，随后出现快速下降，与模型预测结果相吻合。2月12日，由于诊断方式的改变，临床诊断的患者数量增加到新增病例的数量中，日确诊人数激增1万多人，图3中出现一个极端的离群值。2月14日至2月16日，疫情出现小幅度反弹(新增病例分别为1001例，1405例，1548例)，与模型预测结果相一致(预测新增病例分别为1334例，1368例，1391例)。

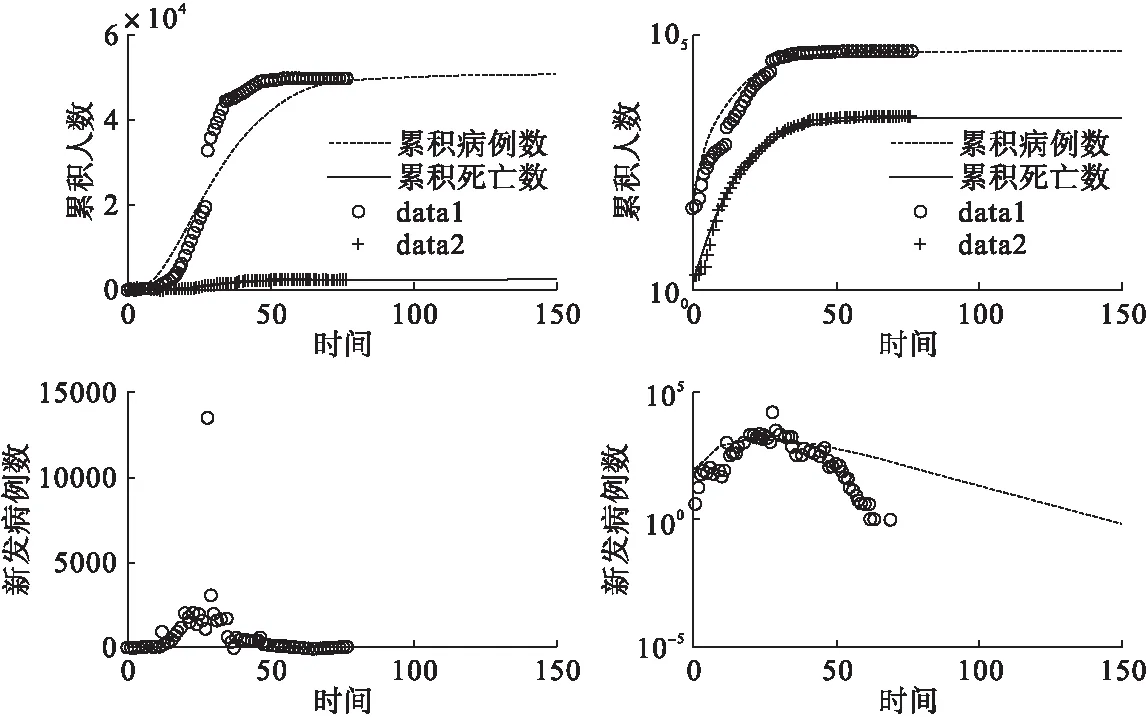
图3 武汉市COVID-19实际日发病人数与模型拟合日发病人数

疫情发生后，武汉市1月23日暂时关闭全市公交、地铁、机场和火车站等交通方式，进入全面封禁状态。本研究比较防控与未防控不同条件下疫情的蔓延趋势，结果见图4。截至疫情流行结束，不采取或未及时采取预防手段时，武汉市将有20.38万人感染，8874人死亡，及时采取防控至少避免15.30万人感染和6425人死亡，有效降低75.08%感染率和72.40%因病死亡率。

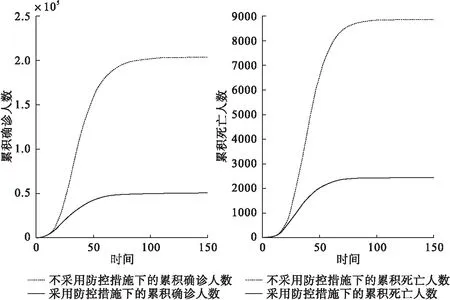
图4 武汉市两种措施下COVID-19疫情流行趋势

讨 论

已有研究发现[5]，COVID-19潜伏期较长且具有传染性，新型肺炎病毒感染者分为有症状和无症状两种类型，无症状感染者在实际工作中很难被发现，这些不利因素导致传染病监测数据复杂多变，给模型评估预测带来难度。面对诸多挑战，本研究基于COVID-19疾病流行特征，集中分析预测武汉市的肺炎流行趋势。相比于既往文献常用的SEIR模型，本模型新增无症状感染者、隔离者、死亡者等因素，在模型结构上取得完善与创新，更符合实际应用需求。

通过拟合累积发病人数及累积死亡人数，我们得到较好的拟合结果，累积确诊病例预测值与实际值的平均偏差约为4.08%。模型对累积死亡人数的预测十分准确，但累积发病人数的早期预测存在较小差异。考虑到实际工作过程中，部分COVID-19感染者不能及时被发现、上报，甚至存在漏报[13]，实时确诊报告人数存在滞后性，所以累积发病人数的预测值表现为开始略高于实际值，随后趋于一致。从日确诊发病数趋势来看，预测值也呈现“先高后低”现象，亦证实这种可能。

由模型拟合结果可知，截至疫情结束武汉市预计50780人感染，2449人死亡，因病死亡率约为4.82%，及时防控降低了75.08%感染率和72.40%因病死亡率。从分析结果来看，武汉的肺炎疫情已经过平台期，正处于逐渐衰退阶段。COVID-19已经成为21世纪以来我国危害性最大，社会影响性最强的重大突发性传染病之一。从防控手段来看，早发现、早隔离、早治疗依然是阻断传染病蔓延的关键思路，对传染病的早期重视和防控能够有效阻止“小病”发展为“大疫”，避免后续产生更多伤亡和损失。同时，我们需要正视预防工作的价值和意义。公共卫生体系的任务使命在于迅速准确地捕捉传染病蔓延的“蛛丝马迹”，及时提供反馈并依据这些信息部署正确合理的防控策略，这一点在未来的体系建设中应当加强。此外，模型结果显示，即使当前疫情拐点已过仍不能放松警惕，将来可能出现连续的小幅度反弹，保持现有防控力度和重视程度是合理且必要的。

本研究依然存在一些局限性。采取防控措施的同时，各方媒体大力宣传和报道，人群对疫情的预防措施愈发重视，导致我们可能忽略个人行为对疫情流行产生的干预[14]，过度估计防控手段对疫情控制的正面效果。另一方面，本研究仅考虑武汉市的疫情变化，没有关注到封城等措施对人口流动的积极影响，忽视了人口流动对于减缓疫情向省外城市蔓延的重要意义[15]。此外，模型中大多数参数在疫情流行期间呈现动态变化，本研究尚未考虑参数的随机化过程，可能会影响模型精确性。后续研究可以从卫生经济学的角度分析，探究采取有效防控措施所避免的经济损失。