基于准Z源直接矩阵变换器的新型空间矢量调制策略研究

李少峰，郭碧翔，程启明，吕 斌，郭凯军

（1.国家电网阜阳供电公司，阜阳236018；2.上海电力大学自动化工程学院，上海 200090）

在交流变频调速系统中，矩阵变换器MC（matrix converter）是一种新型交-交型直接变频装置[1]，其优点为：无需中间直流链路，结构紧凑，易于实现模块化；可以四象限运行，能量可双向流动；正弦输入/输出波形，谐波畸变率小；功率因数任意可调。目前MC逐步取代传统的交-直-交型变频装置，且已在可再生能源发电并网变换器、低速传动、功率因数校正及大功率变换等领域得到应用，因此具有很高的研究和应用价值。MC技术为电网污染的无功和谐波问题提供了解决方案，具有广阔的应用前景[2]。

MC相对较低的电压利用率和复杂的调制方法，使其尚未在工业中被广泛应用[3-4]。为克服电压利用率低的缺陷，相关学者进行了大量研究，提出多种解决方案[5-7]：改进调制方法，即采用过调制方法来提高电压传输比，而该方法以牺牲输出电压和输入电流波形质量为代价，且最大电压利用率也只能有限提高；MC和交流斩波器结合，称之为矩阵电抗变频器，由于MC需要与交流斩波器同步，使得算法复杂，且电压传输比的大小很大程度上依赖于电路和负载参数，输入功率因数低于其它类型的矩阵变换器；通过在输入电压源与MC之间添加升压变压器来提高电压传输比，但此方法增大了系统的体积和成本，且系统的效率和稳定性易受影响。

近年来出现的Z源网络为提高MC的电压利用率提供了可能性[8-9]。基于Z源逆变器的拓扑结构和升压原理，有研究人员将其引入到不同的MC拓扑结构中，并将这类结构统称为Z源矩阵变换器ZSMC（Z-source MC）[10-11]。目前，ZSMC 解决了电压利用率低的问题，能够工作于降压和升压的不同模式，而且比背靠背型变频器成本低，系统效率和可靠性也有所提高。

然而，在实际应用中，为了提供更高的电压传输比，ZSMC必须工作在极端条件下，较低的调制系数和较大的直通占空比约束了输出功率的质量与系统能力的提升，Z源网络的实际升压能力受到限制。此外，由于Z源网络的引入，使得MC的输入电压和电流之间产生不可控的相移，增加了系统的控制难度。而准Z源直接矩阵变换器QZSDMC（quasi-Z-source direct MC）的出现，成功应对了此问题[12-13]。

QZSDMC的调制方法中，如何产生升压所需的直通状态以及直通状态的插入方式至关重要。按注入直通零矢量方法的不同，可分为简单升压[14]、最大升压[15]、3 次谐波注入升压[16]、最大恒定升压[17]、正弦载波PWM[18]和直通状态分段SVPWM[19]等6种调制方法。由于直通分段SVPWM是基于单相直通方式实现的，电感电流纹波较小，能有效减小Z源网络所需电感值，而且具有较大的电压增益和较小的器件电压应力，调制因子的范围大，直流电源电压利用率高，具有较为优良的综合性能。因此，目前常用直通分段SVPWM调制方式。

传统的直通分段零矢量插入方式是将直通状态代替部分零矢量，但其电容电压和电感电流的脉动较大[20]。本文创新性地提出了一种新型直通分段零矢量插入方法，把直通零矢量均分10等份插入到SVPWM调制策略中，该方法通过提高SVPWM周期内直通状态次数，降低Z源网络中电容电压和电感电流的脉动。软件仿真和硬件实验结果验证了本文新型调制方法的正确性和有效性。

1 准Z源直接矩阵变换器的基本原理

1.1 拓扑结构

图1为QZSDMC拓扑结构。由图可见，QZSDMC主要包括输入三相交流电压源、准Z源网络、矩阵变换器以及阻感负载等。其中，Z源网络由6个电容（Ca1、Ca2、Cb1、Cb2、Cc1和 Cc2）、6 个电感（La1、La2、Lb1、Lb2、Lc1和 Lc2）以及 3 个双向开关（Sa、Sb和 Sc）构成。

图中，Ua0、Ub0和Uc0为三相输入电压源电压；UA、UB、UC和 iA、iB、iC分别为三相输出相电压和相电流；Sij为双向开关，i={A，B，C}，j={a，b，c}。

1.2 升压原理

QZSDMC有2种工作状态，分别定义为直通状态和非直通状态，如图2所示。当电路工作在直通状态时，3 个双向开关（Sa、Sb和 Sc）关断，即电路的支路相当于短路，如图2（a）所示；当电路工作在非直通状态时，3个双向开关均导通，即其支路相当于电流源，如图 2（b）所示。

由于输入的对称性，Z源网络电感和电容满足的关系为

对于开关周期Ts，假设直通状态的时间间隔是Tst，则在直通状态下，根据基尔霍夫电压定律，可得

式中：Uab、Ubc和 Uca分别为 ab、bc 和 ca 两相之间的电压；、和分别为 La1、Lb1和 Lc1电感上的电压；、和分别为 Ca1、Cb1和 Cc1电容上的电压；Ui为输入电压。

在非直通状态下电压方程为

如果定义直通占空比D0为

则可以得出Z源网络的输出电压为

式中，D0为直通占空比。

将B=1/（1-2D0）定义为升压因子，则电压传输比q可表示为

式中：mc和mv分别为输入和输出相电流空间矢量调制系数；Uim和Uom分别为输入和输出相电压幅值；φi为输入相位差。

2 准Z源直接矩阵变换器的调制

2.1 双空间矢量调制原理

图3为输入相电流空间矢量调制。根据检测到的三相输入相电压，运用矢量合成原理，可得输入相电压空间矢量UiPh，再由设定的输入相位差φi，可得到期望的输入相电流空间矢量iiPhref所处位置，即

图3中，任意时刻iiPhref可由两相邻的有效矢量iμ、iv（从 i1～i6中选择）和 1 个零矢量 i0（从 i7（a，a）、i8（b，b）和 i9（c，c）中选择）合成。 图中，θsc表示 iiPhref在当前扇区Sci中的位置，其取值范围为[0，π/3]。

有效矢量和零矢量的占空比dμ、dv和d0c可根据伏秒平衡原理和正弦定理得到，即

式中：mc为输入相电流空间矢量调制系数；ip,avg为“虚拟直流环节”的电流平均值。

图4为输出相电压空间矢量调制。输出电流矢量ioPh和期望输出相电压矢量UoPhref分别为

式中：Uom和Iom分别为输出相电压和电流幅值；ωo为输出角频率；φ为输出相电压与输入相电压之间的偏移角；φo为输出电流与电压之间的功率偏移角。

图4中，任意时刻UoPhref可由两相邻的非零开关矢量 Uα、Uβ（从 U1～U6中选择）和 1 个零开关矢量 U0（从 U0（p，p，p）和 U7（n，n，n）中选择）合成得到。图中，θsv表示UoPhref在当前扇区Svo中的位置，其取值范围为[0，π/3]。

有效矢量和零矢量的占空比dα、dβ和d0v可根据伏秒平衡原理和正弦定理得到，即

式中：mv为输出相电压空间矢量调制系数；Upn,avg为虚拟直流环节的电压平均值。

将输入相电流空间矢量调制以及输出相电压空间矢量调制相互结合，可以实现对MC的调制，得到输入/输出的正弦波形和可控的输入功率因数。具体调制过程如下：在每个PWM周期内，共有5 个开关状态对应的开关时间 Tαμ、Tβμ、Tβv、Tαv和T0，分别由矢量 Uα和 iμ、Uβ和 iμ、Uβ和 iv、Uα和 iv以及零矢量决定。这5个开关状态在PWM周期Ts内的作用时间可由式（10）和式（14）相乘得到，即

2.2 新型空间矢量调制

为了实现准Z源的升压，在传统双空间矢量调制策略的基础上，需进行适当修改，合理地插入直通状态，由此本文提出了新型空间矢量调制方法。

在传统零矢量中注入直通零矢量的方法有很多种，因此Z源逆变器的调制方法有很多。按注入直通零矢量方法的不同来分类有简单升压、最大升压、最大恒定升压、3次谐波注入升压、直通分段SVPWM和正弦载波PWM等6种调制方法。表1给出了Z源逆变器在上述各种调制策略下的参数比较，包括升压因子B和调制因子M的关系、电压增益G与调制因子M的关系等。

由表1的6种调制方法比较可知，由于直通分段SVPWM是基于单相直通方式实现的，电感电流纹波较小，能有效减小 Z源网络所需电感值，且具有较大的电压增益和较小的器件电压应力，调制因子范围大，直流电源电压利用率高，具有较为优良的综合性能。故本文采用直通分段SVPWM调制方式。

（1）直通零矢量

通过对电路直通和非直通状态的分析，确定直通零矢量后，结合MC具有的27个合成矢量，从而形成新的调制策略。其中，QZSDMC的直通矢量可以分为3类：单输出相直通、双输出相直通和三相输出直通。单输出相直通方式可以有效减少双向开关的开关次数，被广泛采用。表2所示为输出A、B和C相共计27个单输出相直通零矢量。

（2）新型PWM脉宽分布

为了使QZSDMC在非直通模式下不影响输出电压，传统的直通分段零矢量插入原则是：在1个开关周期Ts内，保证用于合成的有效矢量的占空比不变，用直通零矢量代替部分零矢量，直通零矢量作用时间Tst一般均分成4或6等份插入到SVPWM调制策略上。采用该原则还能减少双向开关的开关次数并降低其功率损耗。

根据式（5）可知，1个PWM周期Ts内，直通状态的作用时间为

因此，可得有效矢量及零矢量的作用时间为

表1 Z源逆变器6种调制策略性能比较Tab.1 Comparison of performance among six modulation strategies for Z-source inverter

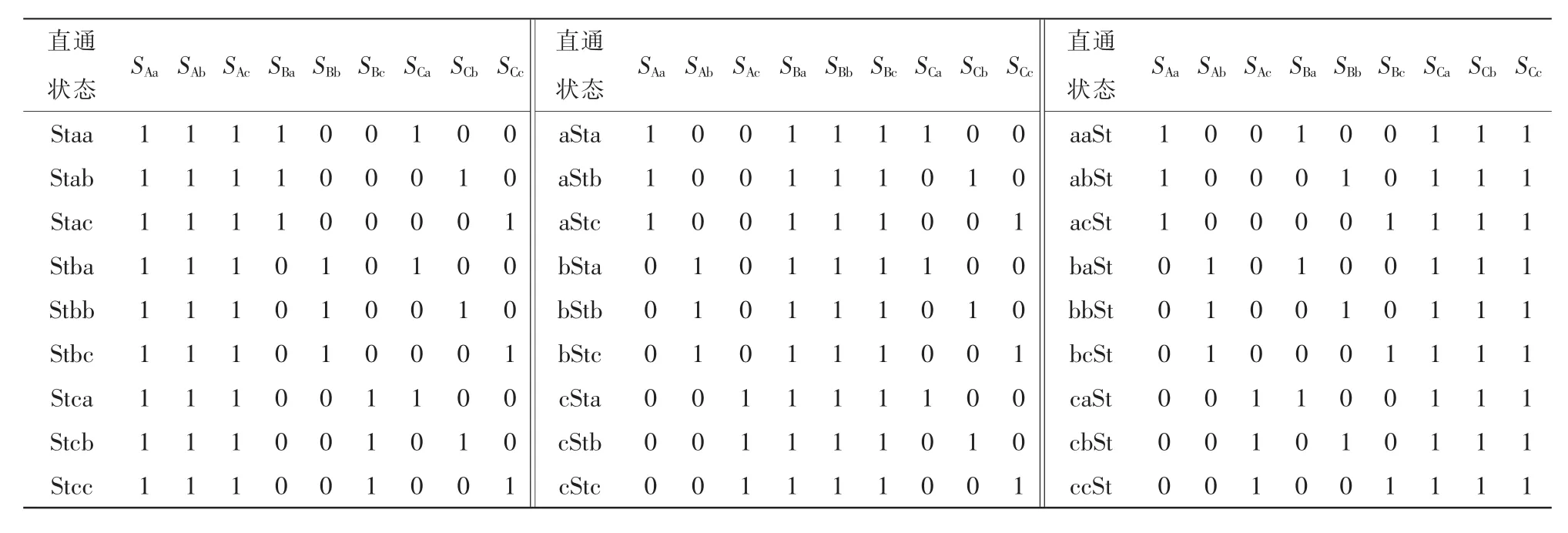
表2 直通零矢量的开关状态Tab.2 Switching states of through-state zero-vector

传统方式把直通零矢量作用时间仅均分成4等份插入到SVPWM调制策略上，将会导致Z源网络电容电压和电感电流的脉动较大，本文研究了一种新型空间矢量调制方法。首先，开关周期的直通零矢量作用时间Tst被等分为10个部分；然后，依次选择合适的直通零矢量，并将它们插入半周期双空间矢量调制的有效矢量之间；最后，调整作用时间以完成整个调制过程。相比于传统方法中等分为4个部分，本文提出的等分为10个部分增加了电感和电容的充电频率，减小了电感和电容所需容量及体积，降低了Z源网络电容电压和电感电流的波动。

假设输入参考电流矢量位于扇区Sci=1中，输出参考相电压矢量位于扇区Svo=1中，则有效矢量由电流矢量i6、i1和电压矢量U1、U2合成。在通过双空间矢量合成的过程之后，形成4个有效矢量（即abb、aab、aac 和 acc），2 个零矢量（即 bbb 和 ccc）以及相应的直通零矢量（Stbb、aStb、aaSt、aStc和 Stcc）。2 种直通插入方式与开关序列如图5所示，图中，T1～T4、T0和Tst分别为在1个采样周期Ts内4个有效矢量、2个零矢量和插入的直通零矢量的作用时间。

3 准Z源直接矩阵变换器的仿真及结果分析

设置输入三相电压源220 V/50 Hz，准Z源网络中电感为2 mH，电容为50 μF，阻感负载的电阻R=10 Ω，电感 L=5 mH。此外，设置调制系数 mc=0.8、mv=0.9，输入相位差φi=0，输出相电压频率为25 Hz。系统的采样时间和PWM周期均设置为0.2 ms。

3.1 系统工作于无升压模式

设置直通占空比D0=0，升压比B=1/（1-2D0）=1，即无升压，无升压情况本文所提方法的仿真结果如图6所示。图中，从上至下依次为输入电压源a相电压和电流、准Z源网络输出相电压、输出A相电压以及输出三相电流波形。

由图可见，准Z源网络的电感起到滤波作用，因此可以省略输入LC滤波器。同样的，由于准Z源网络具有的无功元件，使得输入电流略微超前于输入电压，这可以适当调整输入相位差φi值，达到输入功率因数cosφi=1。输出电压也为类阶梯波形，但由于负载为阻感负载，其电流波形接近正弦波，并且正弦度较高。通过理论计算以及FFT分析可知，输出相电压基波幅值在195 V左右（实际的电压传输比，符合所设置的电压传输比（设置的电压传输比由式（7）可算出

3.2 系统工作于升压模式

设置直通占空比D0=0.25，升压比B=1/（1-2D0）=2，即有升压，其他参数不变。图7为传统插入直通方式和本文所提方法中Z源网络输出电压的对比。

由图7（a）可见，在每等份中，由于直通矢量作用Ts/4时间，时间较长，电压包络线下降较多；而在图7（b）中，由于直通矢量作用Ts/10时间，时间相对较短，在每份直通矢量作用时间内，准Z源输出电压包络线下降较少。将电压包络线的下降值由传统的平均分配至4段变为10段，使得电压波形更为平缓。因此，本文提出了将直通矢量10等分，以达到更优的调制效果。

图8为加入升压后本文所提方法下的仿真结果。由图可见，由于准Z源网络具有升压能力，当设置直通占空比D0=0.25，即升压比B=2时，与相同输入电压和相同调制比的传统矩阵变换器相比，相电压的幅值提升了2倍准Z源网络输出相电压波形符合理论计算值，满足设置的升压比

通过对比图6和图8的仿真结果可知，相比于没有插入直通占空比（即D0=0），插入直通矢量占空比D0=0.25时，电压传输比提高了约2倍（即1.25/0.627≈2），因此准Z源网络直通矢量确实能够提高电压传输比。

图9为本文所提方法下输入、输出信号的频谱分析。由图可见，由于准Z源网络的升压作用，使输出电压幅值增大的同时，负载电流比输入电流小，且基本是无直通时的2倍，满足升压比B的设定。

4 实验验证

为进一步验证本文所提方法的优势，搭建了硬件实物平台进行硬件实验研究，该实验平台的参数与仿真参数基本相同。对第3.2节中升压情况下的调制策略进行了实验论证，结果如图10所示。由图10可见，硬件实验结论与软件仿真结果完全一致。

5 结语

准Z源直接矩阵变换器与传统矩阵变换器相比，能够克服传统拓扑结构电压传输比低的不足，而且允许桥臂出现直通的情况，可降低系统的换流难度，具有很高的研究价值。本文在双空间矢量调制方法的基础上，提出了基于直通零矢量的新调制方法，能够有效降低Z源网络输出电压的脉动。最后进行了软件仿真和硬件实验，通过分析比较实验结果，验证了本文所提方法的正确性和有效性。