数形结合帮助学生有效建构“分数的意义”

姚海燕

【摘要】小学生身心发展的规律以及数学概念的抽象性决定了数形结合思想在小学数学教学过程中的重要地位。为了帮助学生理解、掌握“分数的意义”这一重要且抽象的数学概念，完成对分数意义这一概念的有效建构，课堂上可以充分运用数形结合的方法，以形助数，以数解形，实现数到形、形到数的转化，把抽象思维与形象思维相结合，有效降低学生理解的难度，起到事半功倍的效果。

【关键词】数形结合 分数的意义 有效建构

数形结合就是在研究数学问题时，由数思形，见形思数，是一种可使复杂问题简单化、抽象问题具体化的常用的数学思想方法。分数的意义是比较抽象的数学概念，学生在掌握这一知识时有一定的困难。课堂上充分运用数形结合的思想，可以有效降低学生理解的难度，帮助学生理解、掌握分数的概念，促进学生对分数的意义的建构。

一、以形助数，充分理解单位“1”

“分数的意义”是在学生已初步认识了分数的基础上，进一步深入理解，由感性认识上升到理性认识，概括出分数的意义。单位“1”是认识分数意义的关键，是这一节课的重难点。

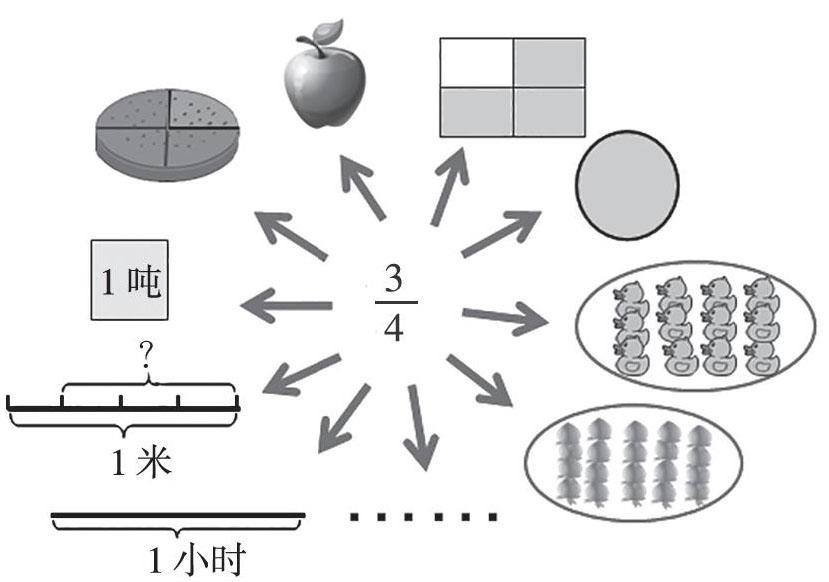
教学中，教师先出示四幅图，要求学生用分数表示涂色部分 。

学生回答后师追问：为什么图不一样却都可以用3/4表示？然后继续提问引发学生思考：那你觉得3/4还可以表示什么？把什么平均分？

教师根据学生回答，课件出示若干图片，在学生充分发表意见的基础上概括出“一个物体”“一个图形”“一个计量单位”以及一些物体组成的“一个整体”，再由它们的共同特点引导学生领悟单位“1”的含义，逐步抽象归纳出分数的意义。

以上过程中，教师先让学生见形思数，用分数表示图中的涂色部分，并说说写出的分数的含义，引起学生对相关旧知的回忆;再引导学生由数思形，“还可以表示什么？还可以把什么平均分？”丰富的答案让学生充分感受到被平均分的对象是非常广泛的，为建立单位“1”的概念积累了具体的感性材料。通过不断地思考、观察、比较、抽象、概括，完成了对单位“1”的认识与扩展，充分发挥了形象思维对抽象思维的支持作用，降低了认知难度。

二、以数解形，正确认识“分数单位”

与自然数、小数单位一样，“分数单位”是一个比较重要的概念，它是后续学习分数大小比较、分数运算的基础，但在教学中，却往往容易被忽视。分数单位是分数的单位，但由于它会随着单位“1”平均分的份数的变化而变化，不像自然数的计数单位（个、十、百、千、万……）那样固定不变，这就使学生理解起来感到抽象、困难。所以，教学中可以借助“形”的生动直观性进行讲解，帮助学生正确认识分数单位。

在学生充分感知的基础上，教师让学生通过观察、比较，感悟到一个分数是由若干个几分之一组成的。教师这时揭示：分数单位就是把单位“1”平均分成若干份，表示其中一份的数。结合上面的两张图学生很容易就理解了分数单位的意义，并意识到：把单位“1”平均分的份数不同，分数单位也就不同。

三、数形结合，沟通单位“1”与整数、分数的关系，完整建构“分数的意义”

分数是一个复杂且重要的数学概念，是连接整数和小数的纽带。为了让学生较好地领悟分数的内涵，在教学了分数的意义和分数单位后，教师可以在接下来的环节中巧妙地运用数形结合，平滑地将整数扩展到分数，把分数和整数统一，帮助学生逐步建构完整的数学概念。

教师先出示图1，把4朵花看做单位“1”，那么2朵花和1朵花分别用什么数表示？你是怎么想的？

接着出示图2，把2朵花看做单位“1”，那么4朵花和1朵花分别用什么数表示？为什么？

再出示圖3，把1朵花看做单位“1”，那么2朵花和4朵花分别用什么数表示？

出示图4，引导学生观察比较，同样朵数的花，为什么用不同的数表示？什么情况下用整数表示？什么时候要用分数表示？关键是什么？

直观的图形与抽象的数学语言相结合，帮助学生更进一步领悟单位“1”的深刻意义与重要性，对刚建立起的分数的意义也有了进一步的认识，更重要的是，沟通了整数与小数之间知识的联系性，帮助学生逐步形成并完善数学知识结构。

小学生身心发展的规律以及数学概念的抽象性决定了数形结合思想在小学数学教学过程中的重要地位。在“分数的意义”这一课的教学中，教师充分利用多媒体课件的演示加强直观教学，以形论数，以数解形，实现数到形、形到数的转化，把抽象思维与形象思维相结合，可以起到事半功倍的效果。数形结合的教学过程帮助学生清晰理解原本抽象的数学概念，有效建构了“分数的意义”，为以后的数学学习夯实了基础。