基于陶行知思想的高中数学教学情境创设探析
2020-06-27蒋浩强
蒋浩强


[摘 要]文章主要阐述基于陶行知思想,在高中数学教学中情境创设的探究,针对陶行知教育思想中的“生活即教育”“教是为了不教”“教学做合一”等相关理念做了简要的阐述,并对其思想如何应用于高中数学教学实践中作了简要的论述,以此体现陶行知先生教育思想的重要性和艺术性。
[关键词] 创设情境;生活即教育;教是为了不教;教学做合一
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2020)15-0054-02
数学新课标指出,基于数学学科核心素养的教学活动应该把握数学的本质,创设合适的教学情境、提出恰当的数学问题,引发学生思考与交流,形成和发展数学学科核心素养,由此可见高中数学教学中情境创设的重要性。由于高中数学比较抽象,所以情境创设其实就是把学生难以理解的知识的“学术形态”转化为学生易于接受的“教育形态”,学生对数学的思考主要来自具体的情境。从学生平时熟悉的实际生活情境出发,提出相应的问题,引导和启发学生积极地思考、主动地讨论和探究,从而学习相关的数学思想方法,获得在实际中如何应用知识的体验。
近代著名教育家陶行知从中国国情出发,提出“生活即教育”“社会即学校”“教学做合一”等三大理论主张。2017版数学课程标准也指出,学生需要用数学的眼光在生活当中捕捉数学问题,主动并灵活地运用数学知识思考和分析生活现象,自主地解决实际问题。所以,在数学教学中,教师应多重视学生的生活体验,把数学中复杂的知识与学生的实际生活联系起来,把数学中抽象的问题与生活中的实际情境结合起来,实施让数学生活化、让生活数学化的课堂教学。陶行知先生还积极倡导“教是为了不教”的教学理念,指出教师在教学时应把握好核心的教学要义:授人以鱼不如授人以渔。本文主要运用部分陶行知教育思想,结合在高中数学课堂教学中的情境创设这一环节的应用,进行简明的论述。
一、构建实际生活情境,让学生学习兴趣得以激发
陶行知先生教育思想的核心就是“生活教育”,所以教师应当多借助学生平时生活中的实际体验来创设教学情境。这种生活化的教学情境,可以使得原本枯燥乏味、抽象难懂的数学知识更直观,让学生感受学习数学的乐趣、体会数学知识的价值,从而激发学习数学的兴趣和学习的积极性,培养正确的数学意识。
[例1]在学习“算法语句”时,需要交换两个变量a和b的值,如果教师直接给出程序框图,学生可能会不易理解,教师可以结合实际生活中的常见例子,直观地创设情境引入。如,若现在讲台上有两个大的杯子A和B,A杯中盛满了水,B杯中盛满了牛奶,如果想将A中的水和B中的牛奶交换位置,应该如何交换呢?教师可以继续发问:“可不可以直接将水倒入牛奶中或直接将牛奶倒入水中?”学生立即回答:“不能,这样的话水和牛奶就会混合到一起了。”“那怎么样处理才能让水和牛奶既不混合,又能交换位置呢?”教师追问。学生会答:“再拿一个空杯子C过来,将水倒入C中,将牛奶倒入A中,最后再将C中的水倒入B中即可。”
教师在此可以总结:同学们认为要完成交换则需要借助空杯子。紧接着教师可以启发学生引出问题:可否编写一个程序框图,交换两个变量a和b的值?能不能直接将a和b直接交换呢?就如同刚刚我们所说的如何交換A杯中的水和B杯中的牛奶问题一样,需要借助于空杯子C才能完成交换,那么按照这个思路,对于变量a和b的交换,则需要借助于一个新的变量c才能完成。此案例将抽象的数学问题转化成学生生活中的实际问题,通过生活中实际问题的解决,从而学习数学问题的解决。
二、创设探究型的问题教学情境,让学生主动“学”
陶行知先生曾多次强调:“好的先生不是教书,不是教学生,乃是教学生学。”这正体现了陶行知思想中“教是为了不教”的理念。新课程标准也明确指出,让学生在自主探究与合作交流中自主构建知识。高中数学本身就具有较强的抽象性、逻辑性,要想让学生更好地掌握所学知识,教师需要科学地构建出可以让学生自主探究的问题教学情境,促使学发现问题、探索问题、解决问题,在整个教学过程中让学生主动“学”。
[例2]二项式定理对学生来说是一个全新的内容,教师教学时可以构建如下的问题教学情境。
问题1:以上两个式子展开后有几项?每一项是怎样构成的?
[设计意图]帮助学生回顾多项式乘法的法则,并引导学生归纳其中的规律:如何快速判断展开式的项数?每一项是怎样构成的?(为后面探究二项式定理做铺垫。)
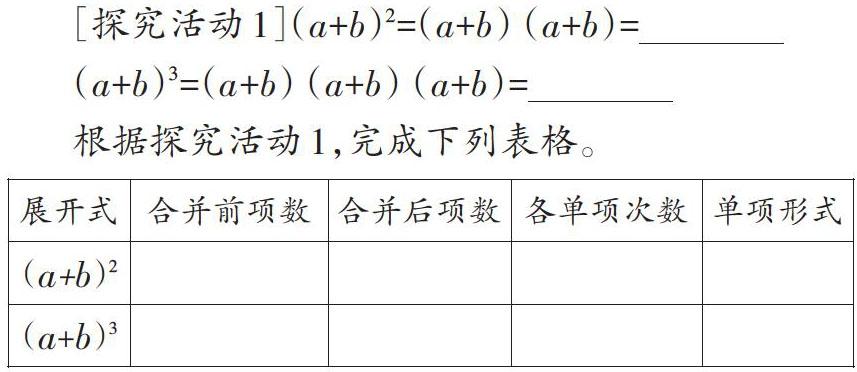
[探究活动1](a+b)2=(a+b) (a+b)=
(a+b)3=(a+b) (a+b) (a+b)=
根据探究活动1,完成下列表格。
问题2:(a+b)2展开式未合并同类项前为什么是4项?
问题3:(a+b)2展开式中ab项的系数为什么是2?
问题4:(a+b)3展开式中ab2项的系数为什么是3?
问题5:口袋中有大小形状相同的a、b两个球,从中摸出1个球后放回,如果有重复的摸3次,摸到1次a球,2次b球会有多少种情况?
[设计意图]通过以上表格数据及4个连续的问题,结合老师的引导,启发学生从展开式中的“项数、次数、项的构成及其系数”等方面来探究展开式的规律,其中的难点在于分析每一项的构成并得到对应项的系数。问题5的设计正是帮助学生将多项式乘法与计数原理建立联系,从而理解ab2的系数为什么是c。(为后面推广到一般情形,探索(a+b)n展开式中各项的系数做准备。)
问题6:你能根据以上结论直接填写下面的表格吗?
请根据以上规律直接写出(a+b)4的展开式(a+b)4=
[探究活动2]由此,你能得到(a+b)n的展开式吗?
[设计意图]让学生经历由特殊到一般的归纳总结,期间离不开对具体的特殊实例的分析。整个过程可以采用让学生独立思考或小组讨论等形式,让学生总结出二项式定理的表达式。
以上通过一系列问题串的设计,引导学生对一些典型和具体的实例进行观察、比较、分析、归纳,从中找出事物的本质属性,主动构建二项式定理的内容,不仅体现了学生学习的主体性,培养了主动学习的能力,而且提升了学生的数学运算、数学抽象、数学建模等数学核心素养。
三、创设探究活动型教学情境,让学生在“做”中学
“教学做合一”是陶行知先生提出的一个重要理论。先生特别强调要在“做”中获取知识。他说:“事怎样做便怎样学,怎样学便怎样教。教而不做,不能算是教; 学而不做,不能算是学。教与学都以做为中心,‘做是学的中心,也是‘教的中心。” 这些话特别强调实践是认识的先导,只有“做”了,“学”才能有收获。另外,学习要在情境中去体验;这也正是新课程倡导的: 学生要乐于探究、勤于动手,培养主动探究、自主学习的能力。
[例3]为了帮助学生更好地理解与掌握椭圆离心率的定义,教师可事先准备如下用具: 一块纸板,两个图钉,一根长约20cm的细绳。
[探究活动1]用图钉将椭圆的焦点固定(即将椭圆的焦距2c固定),然后将细绳的两端固定在焦点处,用铅笔笔尖拉紧细绳,在纸板上画一个椭圆,接着再改变绳子的长度(即改变2a的大小),继续画椭圆,观察这些椭圆“扁”的程度变化情况。
[探究活动2]固定细绳的长度(即2a不变),调整图钉之间的距离(即改变2c的大小),画几个椭圆,观察这些椭圆“扁”的程度变化情况。
问题:大家在动手画椭圆的过程中,发现有什么规律吗?
通过亲自实践,结合学生间的相互讨论,教师再以适当的问题做引导,学生就很自然地得出刻画椭圆形状“扁”的程度的量离心率 e=[ca]。
以上的教学过程是以学生亲自画图为教学情境,通过观察改变a、c两个量后,椭圆形状发生的变化,从中发现椭圆的离心率与椭圆形状的关系。整个过程以学生自主探究为主,很好地体现了“教学做合一”的教学理念。
总之,在高中数学课堂教学实践中,特别是情境创设这个教学环节上,笔者已经深刻地感受到陶行知先生教育思想的重要性和艺术性。在数学教学课堂上,教师不仅要让学生学习数学知识,更重要的是培养学生的数学思想和用数学思维方法去发现问题、思考问题、解决问题的能力。要做到以上这点,也要求教师及时将教育理念和课堂教学相结合,这样才能使学生得到知识素养和学习技能的“双丰收”。
[ 参 考 文 献 ]
[1] 中华人民共和国教育部. 普通高中数学课程标准(2017版)[M].北京:人民教育出版社,2017.
[2] 张奠宙,王振辉. 关于数学的学术形态和教育形态——谈“火热的思考”与“冰冷的美麗” [J]. 数学教育学报,2002(2):1-4.
(责任编辑 黄诺依)