曲梁与拱的正应力分析

陈琦，李振东

（1.兰州理工大学，兰州730050；2.江苏大学，江苏 镇江212013）

1 引言

曲梁与拱因样式多样、造型独特、结构合理而广泛应用于现代结构工程中，但也因其原有曲率的存在，使得曲梁与拱的力学性能较为复杂，研究较为困难。

20 世纪50 年代苏联学者Vlasov【1】建立了经典的稳定性理论，将曲梁的曲率替换，然后代入直梁的平衡方程中得到求解。Usami【2】等基于薄壁构件理论分析的基本假定，推导出曲梁翘曲位移的近似表达式，并推广至拱的研究。本文利用卡氏第二定理【3】以及超静定问题的解得到曲梁的正应力计算公式，并在MATLAB 中以标准实验构件为研究对象，讨论分析了3 种约束条件下曲梁与拱的正应力沿轴线变化的情况，为工程实际提供参考依据，以便于曲梁与拱结构在实际工程中的推广。

2 理论求解

理论研究对象为弹簧钢制（60Si2Mn）的矩形断面曲杆，其圆心角为120°，拱顶有承压支座，两侧拱腰为30°的对称截面。改变其约束方式，构建简支曲梁、二铰拱和无铰拱。取构件任一截面S作为研究对象，其与竖直方向夹角φ 为研究对象。

通过查阅相关资料【4】，得到曲梁的正应力σ 计算公式:

式中，a、Jz为系数；A为截面面积；N为截面S的轴力，N；M为截面S的弯矩，N·m；R为构件的曲率半径，m；y为构件内径到中性轴的距离，m。

2.1 简支曲梁

对于截面S，构件顶端施加集中力P，其弯矩M（φ）和轴力N分别为：

简支曲梁正应力沿截面的变化如图1 所示。

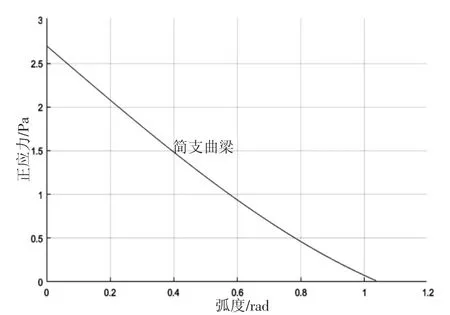
图1 简支曲梁正应力变化图像

2.2 二铰拱

对于截面S，构件顶端施加集中力P，利用卡氏第二定理可得，其弯矩M（φ）、轴力N分别为：

利用最小功原理求得其约束力X1：

二铰拱正应力变化如图2 所示。

图2 二铰拱正应力变化图像

2.3 无铰拱

对于截面S，构件顶端施加集中力P，利用卡氏第二定理可得，其弯矩M（φ）、轴力N为：

利用最小功原理求得约束力X1、X2：

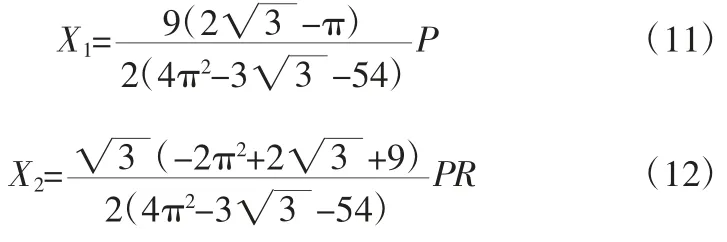
无铰拱正应力变化如图3 所示。

图3 无铰拱正应力变化图像

3 结语

在曲梁与拱的正应力分析中，可以得到简支曲梁与无铰拱的正应力最大截面在φ=0°时，即正应力最大截面在简支曲梁的顶端以及无铰拱的拱顶处。而通过高等材料力学中的理论分析，得到二铰拱正应力最大截面并不存在拱顶处。因此，工程实践中应当加强曲梁与拱在正应力最大截面处的材料强度，以保证工程实践的安全性，同时也为在保证强度要求的前提下节约材料提供了方向。