基于时间序列分析的单采血小板临床需求预测模型研究

彭荣荣 刘芸男 杨小丽* 杨冬燕

(1.重庆医科大学公共卫生与管理学院 医学与社会发展研究中心 健康领域社会风险预测治理协同创新中心，重庆 400016;2.重庆市血液中心，重庆 400015)

近些年,随着我国地市级医院医疗服务水平的提高，罹患再生障碍性贫血、白血病、血小板减少性紫癜等血液病的城乡居民，不再像以前不得不去省级综合医院接受治疗，如今更多地选择到中心血站覆盖的地市级医疗机构就医，致使地市级医疗机构血小板用量迅速增加，中心血站血小板供需矛盾突出，季节性和结构性血小板缺乏时有发生[1]。目前我国采供血机构尚无科学的临床血小板需求预测方法，仅凭相关人员过往经验简单估算，实践中时有血小板缺乏及过期报废现象发生，本研究拟采用时间序列分析方法建立血小板临床需求预测的自回归移动平均(autoregressive integrated moving average，ARIMA)模型，为中心血站制定无偿献血招募及采集计划提供科学依据。

1 资料与方法

1.1 数据来源

获取2006至2016年重庆市6个中心血站每月向医院提供的单采血小板临床用量数据(单采血小板是用细胞分离机单采技术采集的血小板)。

1.2 ARIMA模型的建立

ARIMA模型建立的基本步骤：(1)时间序列分析及处理。对于平稳序列可直接拟合模型，非平稳序列需先进行平稳化处理。使用差分和季节差分分别对存在趋势性和季节性的序列进行处理使其平稳。(2)模型识别与参数估计。根据自相关函数(autocorrelation function,ACF)图和偏自相关函数(partial autocorrelation function，PACF)图的特征，判断其拖尾或截尾情况，初步确定p、q和P、Q值，提出几种备选模型；对备选模型进行参数估计与假设检验，根据t检验结果中的P值进行判定，若P>0.05[2]则参数检验未通过；反之，则通过。然后依据贝叶斯信息准则(Bayesian information criterion，BIC)确定最佳模型。(3)模型检验。对模型的残差序列进行白噪声检验，主要是为了检验残差是否存在自相关性，一方面可以根据残差序列的自相关图判断，另一方面可以进行Ljung-Box Q检验。如果残差序列不是白噪声序列，则需进一步改进模型。(4)模型预测。运用最优模型预测2016年7至12 月每月血小板临床需求量，计算95%置信水平下的置信区间以及相对误差，以验证模型的拟合效果。

1.3 统计学方法

运用Excel软件建立数据库，按月统计单采血小板临床用量，以1个治疗量计算；然后将其导入IBM SPSS Statistics软件进行统计分析。

2 结果

2.1 单采血小板临床用量时间序列分析及处理

绘制2006年1月至2016年6月每月单采血小板临床用量的原始序列图(图1A)，可以看出原始序列存在明显的上升趋势，2006至2013年临床用量逐年上升，2013至2016年上升趋势才逐渐变缓。为了消除原序列趋势性影响，故对其进行一阶差分处理，结果见图1B，可见原序列的上升趋势不再明显。

图1 原始序列图和经过一阶差分后的序列图

绘制原序列经过一阶差分的自相关函数(ACF)和偏自相关函数(PACF)图来检验原序列是否存在季节性，见图2。由图2可见，发现ACF和PACF在滞后12阶均显著不为0，表明原序列还存在季节周期性，以12个月为一个周期。因此，需要对原序列的一阶差分序列进行季节差分，结果见图3。从图3可以看出经过一阶差分和一阶季节差分后序列中每个值都围绕在固定值附近波动，为平稳序列。

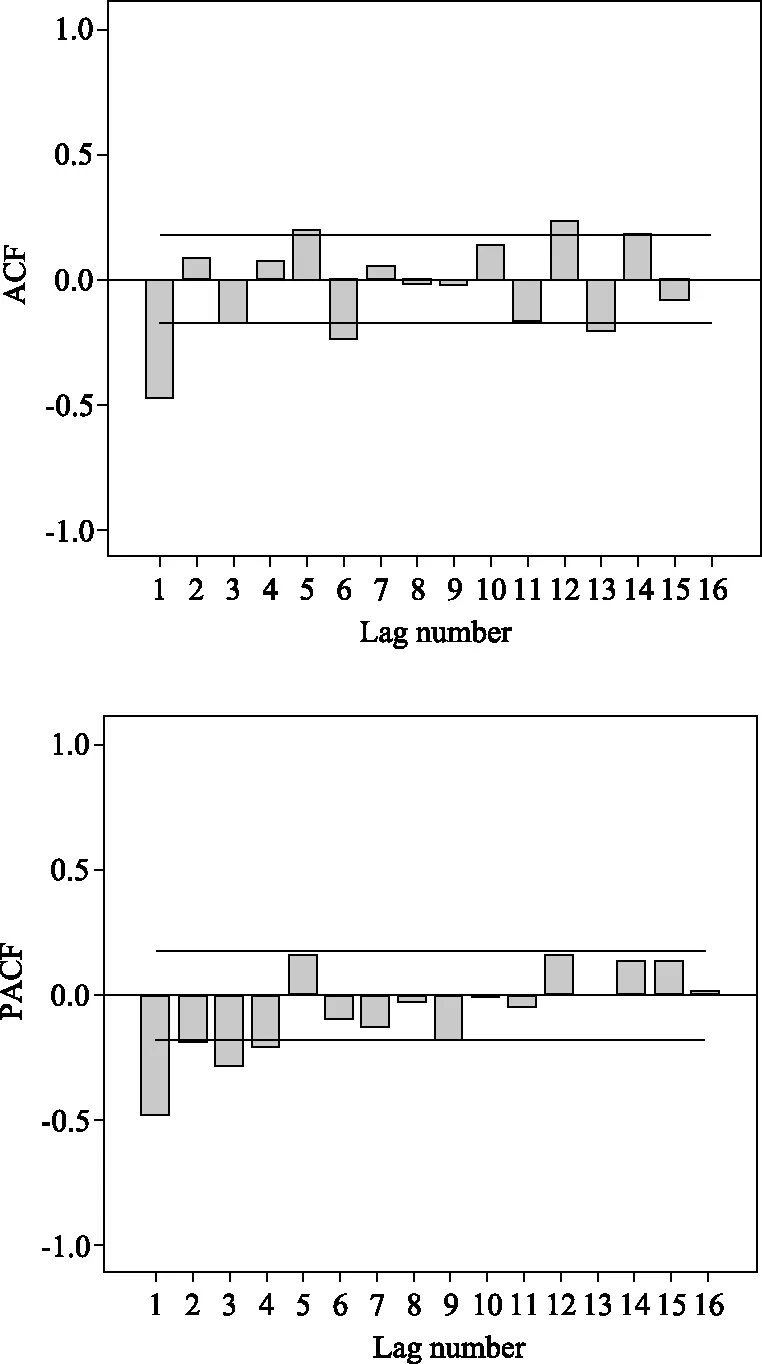
图2 经过一阶差分后的自相关函数和偏自相关函数图

图3 经过一阶差分和一阶季节差分后的序列图

2.2 单采血小板临床用量模型识别与参数估计

由于2006年1月至2016年6月每月单采血小板临床用量序列存在明显的趋势性和季节性，故选用ARIMA乘积季节性模型，即ARIMA(p,d,q)(P,D,Q)s，其中p为非季节自回归阶数，d为非季节差分阶数，q为非季节移动平均阶数，P为季节自回归阶数，D为季节差分阶数，Q为季节移动平均阶数，s为季节长度。因序列的季节周期为12个月，故s取12；由于对原序列进行了一阶差分和一阶季节差分，因此d和D都取1。

绘制单采血小板临床用量序列经过一阶差分和一阶季节差分序列的自相关函数(ACF)和偏自相关函数(PACF)图，见图4。图4可见，ACF在滞后1、5、6、12、13阶都有突出，表明ACF拖尾或者截尾特征不明显，q取0；PACF在滞后1～5阶突出，第5阶后明显收缩，因此判断PACF呈5阶截尾，p取5。同时，ACF在滞后12阶显著不为0，故Q取1；PACF在滞后12阶可以认为是0，故P取0或1。综上可知，识别模型为ARIMA(5,1,0)(0,1,1)12、ARIMA(5,1,0)(1,1,1)12。

图4 一阶差分和一阶季节差分后的自相关函数和偏自相关函数图

识别模型的参数估计与假设检验见表1。从表1可知，识别模型ARIMA(5,1,0)(0,1,1)12和ARIMA(5,1,0)(1,1,1)12的参数显著性检验均未通过(P>0.05)，故需重新选定模型。相关学者[3-4]认为P、D、Q三者取值一般不大于2，即取0、1或2；为了将模型考虑得更加全面，尝试p和q取0的情况。采用从低阶向高阶不断尝试的办法，通过比较各个模型的标准化BIC值，BIC值越小的模型，拟合效果越好[5-6]，最终选定最优模型为ARIMA(0,1,1)(1,0,1)12。

表1 识别模型和最优模型的参数估计值与假设检验

ARIMA: autoregressive integrated moving average;SE:standard error;AR： autoregressive;MA： moving average;SAR： seasonal autoregressive;SMA： seasonal moving average.

2.3 模型检验

图5 单采血小板临床用量ARIMA(0,1,1)(1,0,1)12模型残差序列自相关函数和偏自相关函数图

对最优模型ARIMA(0,1,1)(1,0,1)12进行白噪声诊断。由图5可见，残差序列自相关函数和偏自相关函数基本落在两倍标准差范围之内，即在95%的置信区间内；并且残差序列Ljung-Box Q统计结果显示P值大于0.05，表明残差不存在相关关系。因此，模型ARIMA(0,1,1)(1,0,1)12的残差序列满足随机性假设，为白噪声序列，拟合模型显著有效，适用于临床单采血小板需求量的预测。

2.4 模型预测

应用最优模型ARIMA(0,1,1)(1,0,1)12预测2016年7-12月每月单采血小板临床用量并评估模型的预测效果。预测结果显示，实际值与预测值均在95%的置信区间内，平均相对误差为7.5%(详见表2)，模型拟合图中预测值与实际值的曲线变化趋势基本一致(图6)。多数学者[7-9]认为平均相对误差小于10%说明模型的预测结果精度较高，预测拟合效果好。

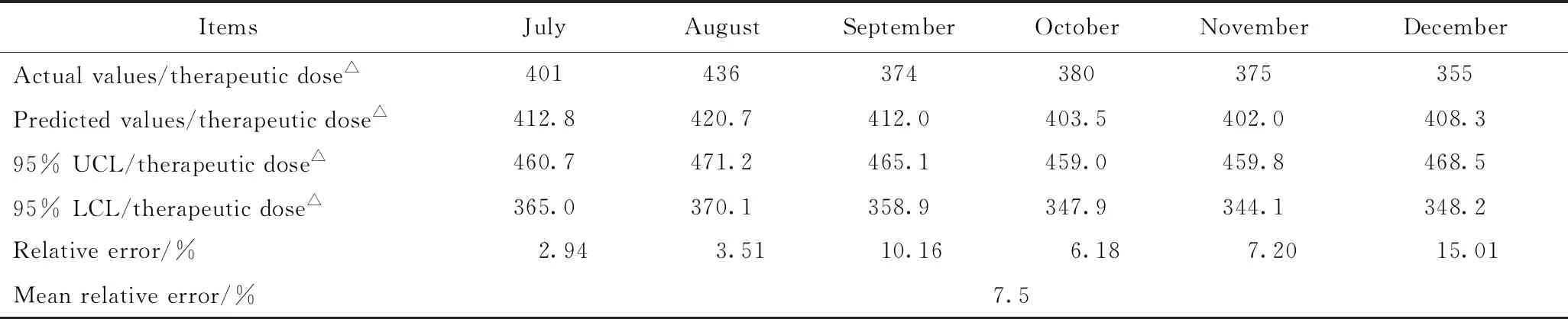
表2 2016年7至12月份每月单采血小板临床用量预测值与实际值的比较

△: one therapeutic dose is 50 mL apheresis platelets;UCL: upper confidence limit;LCL: lower confidence limit.

图6 单采血小板临床用量ARIMA(0,1,1)(1,0,1)12模型拟合效果图

3 讨论

时间序列预测是通过历史数据来分析目标对象随着时间而改变的内在规律，并利用外推机制将这种规律推演到未来，预测目标未来的变化情况，其中ARIMA模型是应用最广泛的时间序列模型[10-11]。ARIMA模型通过不断反复识别、修改和模型诊断，可筛选出最优的拟合预测模型，该模型具有适用性强和精确度高等特点，且能综合分析线性趋势、季节波动和随机误差等因素[12]，适用于与季节周期性相关的临床血小板需求预测研究。

本研究将近些年血小板供需矛盾较为突出的中心血站纳入研究视野，以重庆市中心血站为研究对象，利用中心血站2006年1月至2016年6月每月单采血小板临床用量建立ARIMA模型，运用最终确定的最优模型对2016年7至12月每月单采血小板临床需求量进行预测，预测结果显示，平均相对误差为7.5%，说明各模型的预测精度较高，拟合效果好。

临床上血小板输注主要用于治疗血液病等各种因素所致的血小板数量下降或功能障碍。由于血小板的保存期限短，在温度(22±2)℃的环境下保存时间小于5 d，建立血小板临床需求量ARIMA预测模型，为血小板采集、制备、供给提供科学的依据，增强风险应对能力，使采供血机构提供的血小板量既能满足临床需求，又能避免过期浪费。有研究[13]表明ARIMA模型适宜短期(1年)预测，是由于ARIMA模型是依据历史数据建立的预测模型，并未考虑政府相关政策出台和调整、突发公共卫生事件等外部因素的影响[14-15]。因此，运用ARIMA模型预测血小板临床用量时除需及时更新血小板临床用量数据对模型类型、参数不断完善[16]，以修正拟合效果最佳的模型以外，尚需关注外部因素可能带来的影响。