基于集总参数模型的人工耳蜗圆窗植入位置对残余听力影响分析
2020-06-23倪广健庞嘉高搏蒋刈4戴朴明东
倪广健庞嘉高搏蒋刈,4戴朴明东*
1天津大学精密仪器与光电子学院生物医学工程系(天津300072)
2天津大学医学工程与转化医学研究院(天津300072)
3解放军总医院耳鼻咽喉头颈外科(北京100853)
4福建医科大学省立临床医学院、福建省立医院耳鼻咽喉科(福州350001)
听觉系统受损原因复杂而且是一个不可逆的过程,对人们正常生活、信息交流有不可估量的负面影响,除感觉功能的缺失,更会引起严重的心理问题。据第二次全国残疾人抽样调查结果推算,全国听力残疾者共2780万,其中单纯听力残疾者2004万,多重残疾者776万,且每年新生聋儿约3万名[1]。人工耳蜗(Cochlear Implant,CI)是目前应用最为广泛和成功的神经假体,它为重度到极重度感音性耳聋患者提供了通过电刺激恢复听觉的方法。截止到2017年全国约有6万余人接受了人工耳蜗植入,其中80%植入者为婴幼儿。
经过多年临床观察,发现人工耳蜗植入对语前聋和语后聋患者的康复都会起到积极的作用。电生理研究表明失聪儿童的听觉皮层发展有一个关键期,在此关键期内适当的刺激对听觉感知的形成和言语的发展至关重要[2,3]。CI植入能够重建重度耳聋患者的听力,帮助患者恢复听觉、言语、认知功能,其康复效果受术前听力水平、植入时年龄、使用时间、家人教育程度等多方面综合因素影响[4-8]。
人工耳蜗植入手术中,需要对耳蜗开窗以便电极植入。临床上针对正常结构的耳蜗经常采用的开窗位置包括耳蜗鼓岬、圆窗以及耳蜗顶回[9,10]。电极圆窗植入行径耳蜗自然孔道、植入电极直接、安全有效,较符合刺激电极植入要求[11-13]。Richard等研究表明经圆窗插入电极对耳蜗损伤最小,耳蜗内形成的新生组织最少[14]。Rask-Andersen等认为钻磨鼓阶行耳蜗切开术,在耳蜗内可能产生因骨粉诱导的纤维化和新骨形成,对听神经反应产生负面影响[15]。Hartl等人研究发现人工耳蜗植入后耳蜗在空气传导声激励情况下变化较为明显,从临床的角度表明电极植入是残余听力下降的原因之一[16]。Attias等人也通过动物模型验证了人工耳蜗植入改变了内耳力学特性,进而引起传导性听损[17]。
本文研究基于人工耳蜗植入者的CT影像资料获得圆窗几何结构、植入电极的几何结构和位置,以此进行有限元建模与分析。通过仿真计算得到不同频率下各人工耳蜗植入者圆窗膜的刚度变化情况,进而利用集总参数模型求解得到此刚度变化对残余听力的影响,从理论的角度比较分析不同电极在圆窗的植入位置对残余听力的影响情况。
1 圆窗膜刚度变化
圆窗膜附着于鼓室内壁的圆窗龛内,介于鼓室与耳蜗之间,是中耳与内耳之间的软组织屏障,又称第二鼓膜。人、猴、猫和啮齿动物的圆窗膜超微结构的研究表明,人和动物的圆窗膜均包括三层基本结构:与中耳粘膜上皮相连的外上皮层、核心的结缔组织层和与内耳上皮相连续的内上皮层[18]。有针对中国人颞骨圆窗龛研究发现其圆窗膜横径平均值为1.14 mm(0.8~1.35 mm),上下径平均值为1.65 mm(1.65~2.20 mm)。
本文采用有限元方法建立了圆窗膜的数学模型用于研究其刚度在植入前后的变化情况。真实圆窗膜的结构形态比较复杂,为马鞍状且因人而异[19,20],但是由于其具体形态主要影响高频时的动态特性,实际研究中大多简化为圆形平板状[21-24]。图1为人工耳蜗用户的CT图像,红色包络线显示了圆窗膜结构,图中可以明显看出圆窗膜的结构更近似于椭圆状,蓝色包络线显示了人工耳蜗的植入电极。
本文主要关注圆窗植入电极后对低频残余听力的影响,因此将圆窗膜按照其CT图像二维投影的特征简化为厚度为70 μm的椭圆状平板结构(如图2所示),其边缘参考实际解剖特点假设为固支(即圆窗膜边缘不可移动或转动)。模型中圆窗膜的杨氏模量假设为2×106 Pa,密度为1,200 kg m-3[23,24]。真实情况下圆窗膜与鼓阶内的外淋巴液相接触,构成一个流-固耦合结构。本文在有限元软件ANSYS(v17.0)中采用“solid185”弹性单元模拟圆窗膜,采用“fluid30”流体单元模拟鼓阶中的外淋巴液,以此构建出圆窗膜-鼓阶淋巴液的流-固耦合系统。电极植入带来的圆窗膜刚度变化情况通过限制圆窗膜内被电极占据位置的单元自由度来模拟表示(如图2b所示)。
本文模型对人工耳蜗植入后的圆窗膜进行了若干简化处理,包括:1)假设人工耳蜗的电极不会发生移动;2)假设圆窗膜的厚度和材料属性不会随人工耳蜗电极植入或粘合过程而发生改变。

图1 人工耳蜗病人的CT图像,其中红色包络线显示了圆窗膜轮廓,蓝色包络线显示了电极轮廓。Fig.1 CT image of the CI user,in which red and blue circles show outlines of the round window membrane and the electrode,respectively.
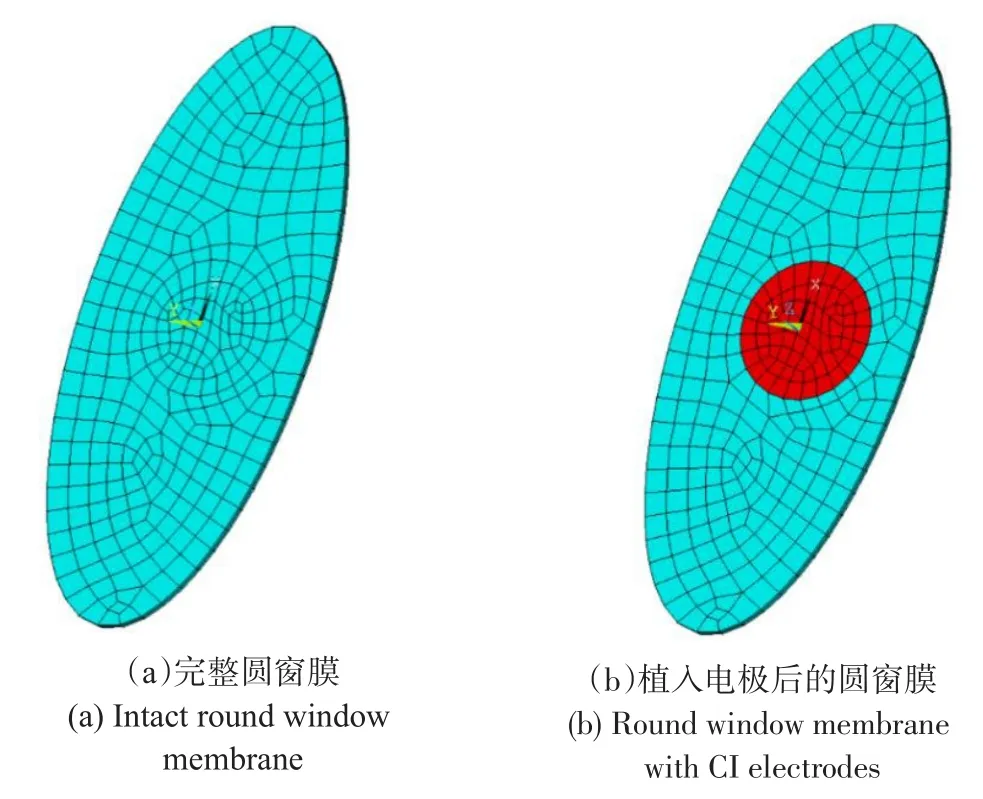
图2 圆窗膜有限元模型Fig.2 Finite element model of the round window membrane

图3 圆窗膜阻抗变化Fig.3 Variation of the round window impedance
圆窗膜的声阻抗可以根据其上的声压与圆窗膜体积速度的比值求得。在具体有限元计算过程中,体积速度计算方法为各单元中节点速度的平均值乘以该单元与法向(压力所在方向)垂直的面积。图3显示了在不同频率下完整圆窗膜及人工耳蜗植入后圆窗膜的平均阻抗变化情况。
考虑到圆窗膜不同简化方式对圆窗阻抗的影响,在此将提出的椭圆形平板圆窗膜模型阻抗与Elliott等人[23]采用的圆形平板圆窗膜模型阻抗进行对比。在对比计算中保持两种形状的圆窗膜面积相等,根据面积公式得到圆形平板圆窗模型的半径。如图4所示,左侧图为本文提出的椭圆形平板圆窗膜模型,右侧图为Elliott等人采用的圆形平板圆窗模型,其中两种模型具有相同的面积,以便于对比。

图4 简化圆窗膜的形状。Fig.4 Shapes of the simplified round window membrane,(left)ellipse and(right)circular.The two shapes have the same area
椭圆形平板圆窗膜模型在完整情况下的阻抗变化在低频部分与已有的Nakajima等实验测量[25]及Elliott等模型计算[23]类似。在低频1 kHz以下,圆窗膜的各部分保持相同的相位运动,与Stenfelt等和Kwacz等研究发现结论相符合[26,27]。区别于Elliott等人采用的圆形平板圆窗膜模型,此椭圆状平板模型还可以得到一些圆窗膜的高阶阵型情况。在不同频率下不同圆窗膜简化形状的阻抗值变化如图5所示,图中实线为圆形平板模型的阻抗值变化,虚线为椭圆形平板模型的阻抗值变化。

图5 不同频率下的不同简化形式下圆窗膜阻抗值变化Fig.5 Calculated impedance distributions of the round window membrane with different simplified shapes,Solid line for circular shape and dashed line for ellipse shape
2 残余听力集总参数模型
本研究的目标是从理论的角度探求圆窗膜由于人工耳蜗植入而产生的阻抗变化对残余听力的影响情况。此处我们假设圆窗膜的刚度变化不会影响耳蜗内传递波的产生,其影响机理是通过改变基底膜基底端上下流体压强差而影响基底膜的响应强度。本文采用的了一种包含中耳、内耳的集总参数模型来求解基底膜响应与中耳响应的比值来表征听力水平的变化[23,28,29]。该模型包含了中耳(Middle ear,ME)、卵圆窗(Oval window,OW)、圆窗(Round window,RW)、前庭水管(Vestibular aque-duct,VA)、耳蜗水管(Cochlear aqueduct,CA)、前庭阶(Scala vestibuli,SV)、鼓阶(Scala tympani,ST)以及基底膜(Basilar membrane,BM),如图6所示。

图6 中耳-内耳简化模型示意图Fig.6 Middle-Inner ear model
图7显示了基于图6而得到的中耳-内耳集总参数模型,其中中耳阻抗(从前庭阶指向中耳)为ZME,基底膜阻抗为ZBM,前庭水管阻抗为ZVA,耳蜗水管阻抗为ZCA,圆窗膜阻抗为ZRW,pME代表中耳近鼓膜处压强,pSV代表前庭阶内的压强,pST代表鼓阶内的压强,pBM为基底膜上下压强差。其中圆窗膜的阻抗为前述有限元模型计算所得,基底膜阻抗取自参考文献,其余各个变量取值参见表1。下列各式中L代表惯性,R代表声抗,C代表顺度。
已有研究表明基底膜上下压强差pBM与中耳处压强pME的比值变化可以作为一个有效指标表示耳蜗所受到的声激励变化。根据图7所示的集总参数模型,可以建立基底膜上下压强差pBM与中耳处压强pME的关系,如下式:


图7 集总参数模型示意图Fig.7 Lumped parameter model
本文以圆窗膜中心点为参考,改变植入电极中心与其的相对偏移位置,选取了10种植入电极相对圆窗膜中心点的偏移方案。图8为带有植入电极的圆窗膜示意图,本研究将圆窗膜简化为椭圆平板结构,长轴半径为2.9 mm,短轴半径为1.2 mm,植入电极半径为0.65 mm。以圆窗膜中心点为参考零点,植入电极中心相对的长轴及短轴的偏移量分别为Δa和Δb。提出的10种植入方案M1~M10的CI植入电极中心相对圆窗中心位置偏移量如表2所示。

图8 带有CI电极的圆窗膜示意图Fig.8 Sketch of the round window membrane with a CI electrode

表1 集总模型变量表。Table 1 Variables in the lumped parameter model

表2 人工耳蜗电极中心相对于圆窗中心的位置Table 2 CI electrode center position with respect to the RW center
利用上述的集总参数模型可以得到不同频率下CI电极不同植入位置对圆窗膜阻抗值的影响。图9显示了不同频率下完整圆窗膜及人工耳蜗植入后圆窗膜阻抗的变化情况,其中红色曲线代表完整的圆窗膜阻抗变化,黑色曲线为CI电极在圆窗膜中心植入的阻抗变化,上述的M1~M10的植入方案分别对应在表中。当人工耳蜗在圆窗膜中心位置植入电极后,与完整圆窗膜的情况相比,植入电极的圆窗膜在低频部分的阻抗有大约6倍的增加,同时第一阶的阻抗极小值出现在约950 Hz附近,这表明圆窗膜因为与其耦合的淋巴液体积减少而出现了有效质量的降低。可以发现,与CI电极位于圆窗中心的情况相比,CI电极中心沿短轴的偏移不会显著改变圆窗膜阻抗,但沿长轴的偏移会降低圆窗的阻抗。
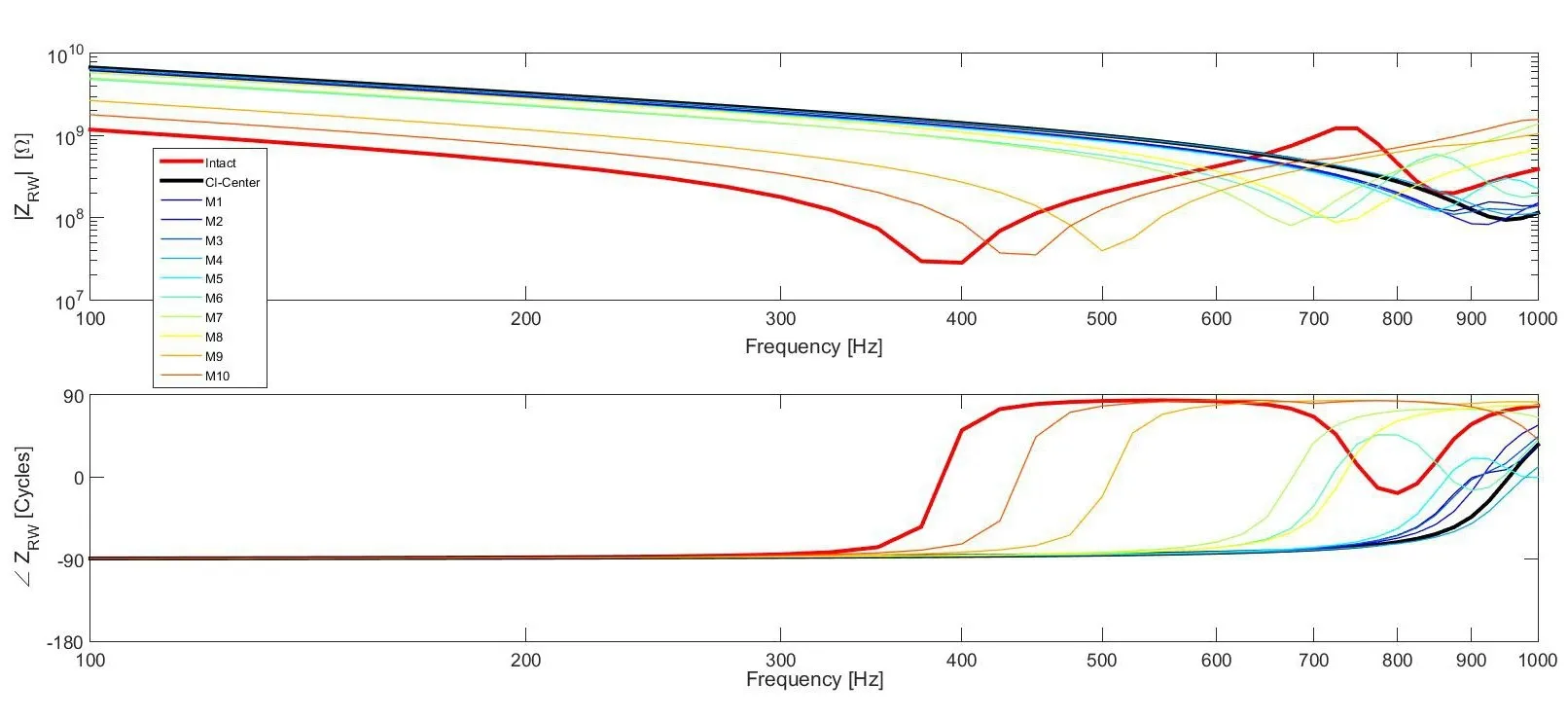
图9 不同频率下完整圆窗膜及人工耳蜗植入后圆窗膜阻抗ZRW变化情况Fig.9 Variation of the round window impedance with frequency when the round window is intact and when it is occupied by a cochlear implant.
图10显示了圆窗膜的振动模式。在频率300 Hz时,图10(a)为完整的圆窗膜振动模式,其中圆窗膜的振动峰值位于中心;图10(b)为CI电极位于圆窗中心时的振动模式,其振动峰值位于圆窗膜两侧;图10(c)为CI电极位于圆窗偏移短轴位置,即M5植入方案的振动模式;图10(d)为CI电极位于圆窗偏移长轴位置,即M10植入方案的振动模式,其振动峰值也产生了相应的偏移。可以发现,当人工耳蜗植入后,由于其阻碍了部分圆窗膜运动,导致了圆窗膜阻抗增加,这一情况势必会影响声波在内耳中传播。
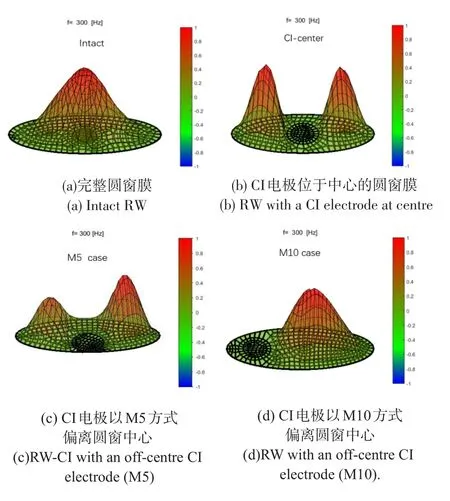
图10 圆窗膜的振动模式Fig.10 Vibration patterns of the round window membrane
3 残余听力变化分析
人工耳蜗植入后引起的圆窗膜刚度变化对残余听力的影响如图11所示,主要表现为1 kHz以内的低频残余听力损失。听力损失计算方法为圆窗膜植入人工耳蜗后基底膜压强与圆窗膜完整情况下基底膜压强之比,从图11可以看到M10对应的植入方案较其他植入方案的听力损失较小,这种情况下电极植入位置相对圆窗中心沿长轴的偏移量最大。

图11 人工耳蜗植入后残余听力的变化情况预测Fig.11 The predicted loss of residual hearing due to the insertion of a cochlear implant via the round window.
4 总结与讨论
在人工耳蜗电极植入手术中对患者原有低频残余听力进行有效保留具有非常重要的意义和作用。本文通过有限元建模与分析,发现CI电极通过圆窗植入会引起圆窗膜刚度的变化,在声波传递过程中,电极植入后的圆窗膜相比完整的圆窗膜其振动模式有所改变,从而阻碍了声波的有效传递。利用残余听力集总参数模型,对内耳和中耳进行参数化模拟,从而得到CI电极在圆窗的不同植入位置对残余听力的影响情况。通过分析,发现沿圆窗膜长轴方向相对中心偏移较大的植入方案对残余听力的影响较小。本文从理论的角度分析了人工耳蜗植入对患者残余听力可能带来的影响,其方法和结论有望为后续人工耳蜗手术植入方案的设计提供参考。
