高考选考科目定级计分和校准的若干问题

温忠麟

（华南师范大学心理应用研究中心/心理学院，广州 510631）

从2006 年开始，陆续有文章指出，高考选考科目成绩（分数或者等级）有必要使用必考科目成绩进行校准（罗冠中，2013；温忠麟，2014，2017；温忠麟，罗冠中，2006，2008，2010），其中包含了两层意思：第一，选考科目成绩不做校准是有问题的，这对考生整体能力较强的选考科目不利；第二，利用必考科目成绩对选考科目成绩进行校准是合理可行的。关于第一层意思，实践已经一再证明了选考科目成绩不校准会带来问题。而且，实践也证明，如果没有用一个合理的方法去校准选考科目成绩，而是碰到一个问题就出台一个应对措施，这样的结果只能是一个问题解决了，另一个问题又出来了，“按下葫芦浮起瓢”。关于第二层意思，国内（特指中国内地）高考至今没有采取用必考科目成绩去校准选考科目成绩的方法，主要原因在于政策制定者甚至部分专家对这种校准方法有疑虑。

本文首先回顾了选考科目成绩不校准带来的问题，举了几个典型的计分方案作为例子，这一部分属于问题的讨论部分，观前预后。随后，文章解答了有关采用必考科目成绩去校准选考科目成绩方面的问题，设计了校准方法的简单变式（包括只加不减方案），这一部分属于问题的澄清部分，释疑解惑。

一、问题从试图摆平各科难度开始

如大家所知，考试分数反映了两个关键指标，一个是考生能力，一个是试题难度。抓住能力和难度就可以把很多问题说清楚。

一次考试结束之后，就固定一个科目而言，试题难度就固定了，分数高低反映了考生在该科目上的能力高低；就固定一个大的考生群体（如一个省或全国考生）而言，考生能力就固定了，科目的平均分（即均值）大小反映了该科试题难度的高低（如果各科满分不同，难度为均值除以满分值）。如果要比较考试分数，要么是用固定科目去比考生能力，要么是用固定考生群体去比科目试题难度（简称科目难度）。若要各科分数具有可比性，前提是要各科的难度相同。难度不同的科目，直接比较分数是有问题的。

高考的目的是评价考生能力以选拔考生，最后要比较的是考生能力而不是科目难度。所以，合理的高考评分计分方案应当力求消除不同科目难度的差异，也就是说，设法让各科难度尽可能相同。

考试分数的分布在很大程度上由均值和标准差决定（正态分布，则完全由均值和标准差决定）。均值反映难度，而标准差与区分度有关。本文在重点考虑均值之外，也会考虑标准差，或者两者一并考虑的分数分布。简言之，考虑均值相当于考虑了难度，考虑标准差则在某种程度上考虑了区分度。

（一）没有选考科目的情形

在没有选考科目的时候，各科考生群体可以认为是相同的，个别缺考的情况可以忽略不计。这时候，用平均分除以满分值就反映了难度。如果满分值相同，两科的难度相同当且仅当平均分相同。

当然，如果能在出试题的时候就让各科试题难度相同，那就没有后面的问题了，比如，据说有的考试机构会在事前规定一个难度指标（如0.7）。但是，难度是考试以后才能计算出来的。由于不同科目的命题、评卷人员不同，因此很难提前设置一个评分标准使得难度等于预设的数值。例如，同是满分值150，语文和数学的原始分数平均分可能会相差30 多分（温忠麟，罗冠中，2008）。

在1985—2006 年间，我国许多省份在高考中采用了平均分为500、标准差为100 的标准分（范围100～900）。在没有选考科目的情形下，使用标准分可以消除各科难度差异（同时消除了各科区分度差异），摆平不同科目的难度，是比较合理的做法。具体来说就是，各科标准分的平均分（都是500）相同、满分值（都是900）相同，各科的难度也就相同了。因此，使用标准分，各科分数有可比性，而这个可比性提高了合成高考总分的合理性。

（二）有选考科目的情形

在有选考科目的时候，即使各科能设置评分标准使得难度等于预设的数值（如0.7），也不能说各科的难度就真的相同了，因为各科考生的整体能力可能是不同的，原始分均值已经无法反映难度了。

而且，在有选考科目的时候，通常的计算标准分的方法也有问题（温忠麟，罗冠中，2006）。这种做法不仅将各个选考科目的难度变成一样了，而且将不同选考科目考生群体的分数分布也弄成相同了。由于分数反映了能力，因此这就相当于将各科考生的能力分布也弄成一样的了。如果各个选考科目考生群体的整体能力相近（就像随机分派那样），这样做的问题不大，但现实是选考物理的考生整体能力较高（温忠麟，2017），因此使用标准分对物理科考生（尤其是中位数以下的考生）最不利。广东省从1999 年开始实行“3+X”并沿用1985 年开始使用的标准分以来，选考物理的考生比例逐年下降得很厉害，因此在2007 年又退回去使用原始分。但使用原始分还是有问题（各科难度摆不平），结果便是在 2010 年放弃了选考科目。由此可见，在有选考科目的情形下，使用原始分不妥，使用通常的标准分算法也不妥。

二、选考科目摆平难度引发的连串问题

在有选考科目的情形下，由于考生群体的能力高低不平，此时要摆平各科难度的做法是有问题的。因为在摆平难度的时候，各科考生群体的成绩（以及成绩反映的能力）也被抹平了。

（一）新高考第一批试点的选考科目计分问题

新高考第一批试点省（市）（上海和浙江）选考科目使用的是所谓的比例等级制计分，不少学者对此计分方法所导致的问题多有讨论（例如：陈爱文，胡银泉，2017；柯政，2016；王小虎等，2017；于涵等，2018）。为了比较前后三批试点的选考科目计分方案及其问题，这里对第一批的计分方案也作一些简要介绍。比例等级制的做法是预设比例按考生分数排位划分等级并赋分。以上海为例，11 个等级从高到底的比例依次为：最高的A+占5%，接着的9 个等级各占10%，最低等级E 占5%（见表1）。由于相等成绩的考生等级要相同，而最低等级的划分还有其他规定条件，因此在实践中上述百分比只是一个约数。这就意味着，一个考生在选考科目上的最后得分，与该科试题的难易没有关系，而是取决于他在该科分数上的排位。在这一点上，选考科目实行比例等级制赋分与在选考科目使用标准分（这是1999 年—2006 年间广东实行“3+X”时的做法）在本质上是相同的。也就是说，如果成绩（按百分等级）的排位相同，那么最后的得分也就相同。这种做法在摆平选考科目难度的同时，也抹平了不同选考科目考生整体能力的差异。

表1 2017 年上海高考选考科目等级、比例与赋分

这个方案的问题出在两个方面：一个与难度有关，另一个与区分度有关。先说第一个问题。因为比例等级制类似于标准分，在摆平难度的同时也抹平了不同选考科目考生的整体能力差异，因而对科目整体能力较高的考生不利。这对物理科的影响较大，容易直接导致选考物理的考生变少。为了补救，上海和浙江都出台了“保底”措施：如果物理考生人数少于保底人数，按保底人数（上海物理保底人数是15000）计算，从高到低给考生定级赋分。这种设计的不合理之处很明显：如果该科考生人数超过保底人数，考生会继续吃亏；如果该科考生人数只有保底人数的一半左右，那么最差的一个考生也可以得到C+等级（55 分），也是不合理的。第二个问题是分数区间[40，70]的全距（最大值减去最小值）只有30，与必考科目的全距150 比较，标准差小了很多，因而区分度也低了很多。这种计分方法会让选考科目变得不重要，因为在这些科目上付出再多的努力也多不了几分。

第一个问题会导致选考物理的人数受到影响，第二个问题会让选考科目发挥的作用不大。设想一下：如果非常多的人不愿意选考物理，或者说选了的人也不会怎么努力学习，这将产生什么样的结果？不难想象，这样的选考科目计分方案会对我们国家的教育乃至社会发展产生什么不可估量的影响。

（二）新高考第二批试点的选考科目计分问题

在新高考第二批试点中，山东方案是一个代表。它与前面选考科目相同的地方在于还是采用比例等级制，不同的则是等级比例的设置和赋分规则：将每个选考科目的卷面原始分数，参照正态分布划分为8 个等级并确定相应比例（见表2）；将8 个等级内考生的原始分数依照等比例转换法则分别转换到8 个分数区间（最后一列），得到考生的等级成绩（见图1）（山东省人民政府，2018）。

表2 山东高考选考科目等级、比例与赋分

图1 山东高考选考科目等级比例及计分规则

相对于上海的方案而言，山东方案确实改进了不少：一是分数区间变大，增加了区分度；二是使用正态化等级比例而不是上海那样的均匀等级比例（两端除外）；三是避免了同级必定同分的现象，使同一等级内原始分数的差异信息得以保留（于涵等，2018）。然而，这个方案还是在把各科难度摆平（严格来说是几乎摆平）了的同时也抹平了不同选考科目考生的整体能力差异。下面给出详细解释。

以B 级为例。得到B 级考生的原始分数有一个区间，原始分数在区间中点以上（以下）的考生得分高于（低于）75.5（区间71～80 的中点）。如果原始分数在区间中点以上和以下的考生人数一样多，那么B 级考生的等级成绩平均分正好就是75.5。如果所有级别都是这种理想状态，那么考生的等级成绩平均分为：

其实，根据等级比例的对称性，我们也容易知道平均分等于最小值21 与最大值100 的均值。一般情况下，没有上述的那么理想（通常是越靠近科目平均分的人数越密集），因而每个等级的平均分与理想状态会有少许差异，但每个等级上的差异往往有正有负。正负抵消的结果是每个选考科目平均分与60.5 会很接近，尤其是当考生人数比较多的时候（一个选考科目的考生一般都过万人）。

退一步说，即使各科的等级成绩平均分不完全相同，也改变不了对物理考生不利的状况，甚至可能物理考生的这个平均分还比其他科考生的低呢。所以说，山东方案，还是和上海方案一样对物理考生不利。而且，因为选考科目的分数范围比上海方案大，选考科目的重要性比较高，因而对物理考生的不利情况也会超过上海方案。

第二批试点中的海南方案值得提一下：等级考试成绩使用标准分计入高考总成绩；高考录取总成绩将由统一高考的语文、数学、外语3 个科目成绩和考生自主选择的学业水平等级考试的3 个科目成绩组成，以标准分呈现（海南省人民政府，2018）。具体来说就是，必考科目和选考科目都转换为正态化标准分作为单科分：均值180、标准差30、分数区间[60, 300]。在合成总分的时候，必考科目权重为1.5，选考科目权重为1，6 科相加成总分，然后再将总分转换为正态化标准分作为高考综合分：均值500、标准差100、分数区间[100, 900]（海南省教育厅，2020）。

首先，海南方案在必考科目使用标准分，比其他使用原始分的方案要合理，这一点是很值得肯定的。其次，我们可以看一下选考科目在方案中的重要性。选考科目与必考科目的分数全距比值，上海的是0.20，山东的是0.53，海南的是0.67。这个比值越小，说明选考科目在高考总分中越不重要，其考生越没有努力的动机；反之，这个比值越大，选考科目越重要，对整体能力高的选考科目考生群体越不利（在选考科目使用标准分或者比例计分的情况下）。

相对于上海方案和山东方案来说，海南方案的选考科目重要性较高，对整体能力高的选考科目考生群体比较不利，但与当年广东“3+X”的标准分方案（温忠麟, 罗冠中, 2006）相比较而言，海南新高考方案有下面几方面的改进：一是当年广东方案中选考科目与必考科目的标准分合成总分的权重相同，即选考科目与必考科目的分数全距比值是1，而海南方案的这个比值降为0.67；二是当年广东方案只有1 个选考科目，海南方案有3 个选考科目。综合上面两点可知，海南方案中的任何单个选考科目的重要性远低于当年广东方案的选考科目，这样就减少了因为使用标准分对某些科目带来的不利结果。具体来说就是，与当年广东使用的标准分方案比较，海南方案对物理科考生的不利程度减轻了很多。

海南新高考方案还有一个改进就是，单科标准分的区间由[100, 900]变成[60, 300]，压缩了分数间距，可以解决新高考选考模式下选考人数少的科目分数稀疏的现象。这可以避免单科原始分的一分之差可能导致单科标准分甚至综合标准分的不合理差距。

（三）新高考第三批试点的选考科目计分问题

与前两批试点相比，以江苏省为代表的第三批方案有较大的变化：必考物理或历史。具体来说就是，除了语文、数学、外语3 科必考外，首先在物理、历史中选择1 科，再从思想政治、地理、化学、生物中选择两科，考试分数计入考生总分。必考三科使用满分值150 的原始分（这与上海、山东的一样），选考科目满分值为100 分。物理、历史科目以原始分计入总分；其余科目以等级分计入总分（江苏省人民政府，2019）。

这种做法可以解决前面两批试点中许多考生不愿选考物理（还有历史）的问题，但得到的结果是：“理科生”必选物理，“文科生”必选历史。如果招生的时候严格走两条线（如计算机专业招物理考生、文学专业招历史考生），就不存在这两科分数的可比性问题，但在现实中有不少专业是兼招的（如心理学专业同时招物理和历史考生），这样就有选择物理或历史哪科更有利的问题。与在选考科目使用比例等级制相比，直接使用原始分有可能对物理科考生更加不利，因为物理科的平均分比历史科的低。

既然物理或历史必考，那剩下四个选考科目对哪一科考生会比较不利?多数人担心的是化学。原因有两个：一是重点大学需要化学的专业比需要生物的专业多，因而这两科相比有更多优秀考生选考化学（一般考生避强选弱就可能不会选化学）；二是化学的内容较多、备考需要较长时间（一般考生避难选易也可能不会选化学）。四个选考科目如果还是使用比例等级制（加上“如果”是因为还未见公布具体做法），江苏方案中的化学科可能会面临第一批方案中物理科的局面，即选考化学的人数会减少。

三、选考科目成绩合理的校准方法：摆平各科难度但不抹平考生群体成绩

从上面讨论可知，目前国内选考科目的定级和计分方法都是在摆平各选考科目难度的同时也抹平了各科考生的群体成绩，而抹平成绩与各科考生群体实际上的能力差异是矛盾的，这就是问题的根源。一种合理的做法是基于必考科目成绩对选考科目成绩进行校准（温忠麟，2014，2017）。校准方法有多种变式，其中一种变式是组别能力指数（罗冠中，2013）。从2012 年开始，香港就在中学文凭考试中采纳了该方法。多年的实践证明，该方法合理可行，不会系统出现考生选科时的“避强选弱”和“避难选易”的问题（温忠麟，2017）。

为何国内高考不设计一种基于必考科目成绩对选考科目成绩进行校准的方案呢?从部分政策制定者和专家那里，我们了解到了缘由，并收到了有代表性的看法和意见反馈：

（1）基于必考科目的校准方法复杂，难以接受；

（2）对于考生而言，加分容易接受，减分很难接受；

（3）回归分析不能用来做等值；必考科目与选考科目没有因果关系，不适合用回归来做预测；

（4）用必考科目成绩来校准的话，如果一个考生很拔尖但他的选考科目考生群体在必考科目上的表现比较差，那么他会吃亏。

下面我会逐一回答并澄清这些问题。

（一）基于必考科目成绩的选考科目成绩校准方法可以很简单

基于必考科目成绩对选考科目成绩进行校准，这是一类方法，它有多个不同的变式，有的设计得比较复杂（温忠麟，2017），但也可以设计得很简单。这里介绍一种比较简单的方法。

首先，使用规定的比例等级表对全体考生的必考科目进行定级。为了明确起见，这里以山东省的等级赋分表为例（见上表2），但暂时不会涉及等级赋分，只用到等级比例（如A 等级占3%，等等）。根据这个等级表，每个考生在语文科和数学科各有一个等级。

考虑到必考科目语文、数学和英语中有两个都是文科科目，所以比较公平合理且简单的做法是：只基于语文和数学两科成绩对选考科目进行校准。现在考虑某个选考科目，我们以物理科为例。假设物理科考生有4%的人在语文科获得A 等级，有10%的人在数学科获得A 等级，则物理科考生在语文和数学两科获得A 等级比例的平均值为7%。那么，就规定物理科考生7%的人获得A 等级（而不是等级表上的3%）。同理可以计算物理科其他等级的人数比例。有了等级比例就可以得到等级切分点，然后就可以按等比例转换法则（见上图1）计分了。

这种校准方法的优势在于，一方面它使物理科等级比例与物理科试题难度无关，不论物理科试题的难易程度如何，其等级比例完全由物理科考生在语文和数学上的表现所决定。另一方面，它没有把物理科考生的成绩拉平到与其他选考科目上的一样。

关于这种校准方法的合理性我在以前的有关文章中有详细讨论（温忠麟，罗冠中，2006，2010），简单来说就是：既然不同选考科目的试题难度不同，考生群体能力也不同，而最后的成绩又要有可比性（计入总分进行比较），那我们只好以考生在必考科目上的表现来进行比较，以确定各科考生的群体能力。具体到每个考生，虽然不一定考生的语文、数学成绩好，其选考科目成绩就一定好，但选考科目考生群体（往往上万人），在各个科目上的能力分布可以认为是近似的。

（二）一个变式：校准选考科目成绩时只加不减

对于考生及其家长而言，加分容易接受，减分很难接受。校准选考科目成绩一个妥协的变式是在比例等级制基础上只加不减，这样也比不校准要好很多。

还是以山东方案的等级比例表为例。对选考科目只加不减的做法是，从高级别到低级别依次往下，使用累计比例进行计算和比较，然后按只加不减的规则来定等级比例。首先考虑A 等级比例：如果按校准方法计算的A 等级比例为5%（高于表中比例3%），则使用5%；如果计算的A 等级比例为2%（低于表中比例3%），则使用3%。然后考虑“B+及以上等级”比例（即累计比例），如果计算的“B+及以上等级”比例为11%（高于表中累计比例10%），则使用11%；如果计算的“B+及以上等级”比例为9%（低于表中累计比例10%），则使用10%。往下依次考虑“B 及以上等级”比例，“C+及以上等级”比例……最后是“E 及以上等级”比例为100%（有可能之前某一步的累计比例已经达到100%，后面的就不用计算了）。

表3 是选考科目X 科只加不减校准方案的一个示例。第二、三行是设计的比例和累计比例（来自表2）。第四、五行是X 科考生在必考科目获得的等级比例和累计比例。在每个等级，取设计的等级累计（%）和X 科考生的必考科目等级累计（%）较大者，作为X 科等级累计（%）（倒数第二行），就可以计算X 科等级比例（%）（最后一行）。例如B+等级，有11%的X 科考生在必考科目上获得“B+及以上等级”，大于10%（设计的“B+及以上等级”），则X 科获得“B+及以上等级”的比例为11%（这时比设计的高就是加了）。又如B 等级，有24%的X 科考生在必考科目上获得“B 及以上等级”，小于26%（设计的“B 及以上等级”），则X 科获得“B 及以上等级”的比例为26%（这时跟随设计就是不减）。

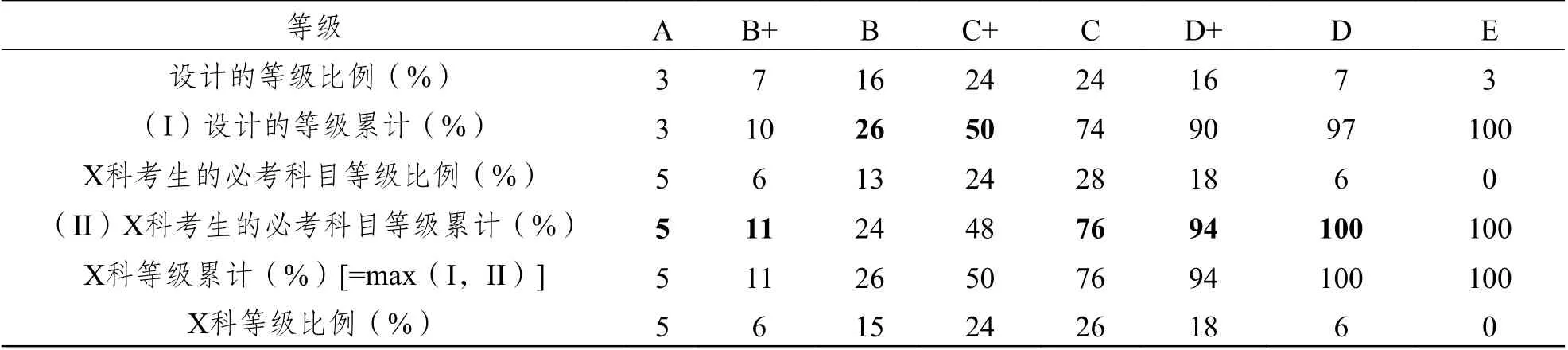
表3 X 科只加不减的等级及其比例

有了上面的那些累计比例，自然也就可以从上到下地计算每一个等级的比例。其实，根据累计比例，已经可以得到每个等级的切分点，也就划分了等级。但要留意的是，必须按表3 示范的那样用等级累计比例去只加不减，而不能像本文第三部分第一节中所介绍的那样计算每个等级比例去只加不减。原因很简单，如果每个等级比例都只加不减，那么所有等级比例之和就不止100%了。

还有一种只加不减的校准方法是：只对某个或某几个选考科目进行校准，也就是针对那些不校准便对考生不利的科目。只加不减的校准方法比一般的可加可减的校准方法更容易被接受，尤其是在刚开始的时候。

（三）选考科目分数校准中回归分析的作用

因为基于必考科目成绩的选考科目成绩校准方法的一些变式在某个环节会涉及回归分析，例如香港的中学文凭考试中使用的组别能力指数校准方法（罗冠中，2013）就有回归分析的环节，因此有人质疑“回归方法不能用来做等值”“必考科目与选考科目没有因果关系，不适合用回归方法做预测”等等。前一个质疑说明质疑者没有理解回归在其中扮演的角色，而后一个质疑说明质疑者没有明白回归与因果的逻辑关系。由于两个质疑都与回归有关，所以我放在本小节一起讨论。

没错，回归不能用来做等值，所以明晰回归在选考科目成绩校准方法中的作用很重要。香港在中学文凭考试中使用的组别能力指数校准方法中的回归分析，是用来找权重的，而不是用来做等值的。本文第三部分第一节中介绍的方法，其实是将语文和数学的权重当作一样来看待，所以用的是等级比例的平均值。实际上，物理与数学的相关往往大于物理与语文的相关，而历史与语文的相关往往大于历史与数学的相关。所以，用必考科目成绩校准选考科目成绩的时候，使用不同的权重是更好的做法：校准物理科成绩的时候，数学权重大于语文权重；校准历史科成绩的时候，语文权重大于数学权重。香港中学文凭考试中必考的四科（中文、英文、数学和通识）都用来校准选考科目成绩，使用了回归方法去找四科的权重。不难理解，这样找出来的权重，比用各科相等权重去校准要好。

按温忠麟（2017）的分类，香港中学文凭考试的组别能力指数校准方法属于强假设下的校准方法。此外，笔者也还提出了一种弱假设下的校准方法，其中用到了多重相关系数R，这也是通过回归分析得到的，而这里就涉及到了回归预测的问题。

回归不能做等值转换的一个原因是，回归方程中两个变量的地位是不平等的，而等值关系中两个变量是平等的。但如果只是用回归来做预测，关键就在于能否精准预测到误差可以忽略不计的问题。用一个（或多个）变量去预测另一个变量，能否通过回归精准地预测，这取决于相关系数（或多重相关系数）的大小，因为只有相关系数（或多重相关系数）很接近1 时，才能进行精准地预测。不同科目的成绩，通常相关系数都远小于1，所以单个的测验分数不能通过回归去预测。但就群体均值的预测而言，如果群体比较大，误差则会很小。这里以通过身高来预测体重为例，试作说明。假如只是预测一个身高1.7 米的单个人的体重，那么预测出来的体重与实际体重出入超过10 公斤都可能，预测误差很大。但对于平均值为1.7 米的一群男性来说，预测他们的平均体重，会相当准确。而如果要预测的男性群体有1 万人，那么误差大约是0.1 公斤（温忠麟，2017）。在这里，身高与体重谈不上等值的问题，但却可以用一个变量去做另一个变量的均值预测。

或许有人会接着质疑：上面说的群体均值的预测误差很小，指的是从大总体中随机抽取的一群人，而现在选考科目考生群体不是随机抽取的，那还可以预测吗?这个说法有点道理。以选考物理科的考生为例，如果放到全体考生来看，选考物理科的考生的物理平均成绩，应当比随机抽取的一群考生（该群考生的语文和数学成绩与选考物理的考生群体的语文和数学成绩相当）的物理成绩要好。这就说明，回归预测的成绩只是选考物理科的考生平均成绩的一个下限，选考物理科的考生平均成绩至少应当校准到预测值那里。换句话说，物理科考生用回归预测值去校准还是太保守了，这就是为什么可以建议在R 与1 之间让专家设置一个值去校准（温忠麟，2017）。

对于“必考科目与选考科目没有因果关系，不适合用回归方法做预测”这个质疑，也很容易证明它是一个错误的看法。这个质疑的逆否命题为“适合用回归方法做预测的关系，是因果关系”。一个命题与它的逆否命题等价。众所周知，“适合用回归方法做预测的关系，是因果关系”是错误的，所以“必考科目与选考科目没有因果关系，不适合用回归方法做预测”也是错误的。

（四）选考科目分数校准后拔尖考生不会吃亏

选考科目的分数校准是在群体层面进行的，如果一个选考科目群体在必考科目上的表现较差，意味着校准后该群体在选考科目上的成绩也比较差。那么，一个拔尖的考生，如果其所在群体的必考科目成绩比较差，他会不会吃亏呢?

如果考生甲在一个选考科目上拔尖，那么只要该选考科目群体有少数人在必考科目上获得A 等级，考生甲在该选考科目就可以获得A 等级了。如果考生甲在必考科目上拔尖，在选考科目上应当也不会太差（因为他可以选考他比较擅长的科目）。如果他的选考科目群体在必考科目上的表现较差，说明该科考生整体能力较低，那么他的必考科目表现会更加突出，即所谓的“小塘大鱼效应”（Ludtke et al.，2005）。就算他的选考科目成绩一般，在录取的竞争中也还是更有对比优势。道理很简单，因为甲在必考科目上拔尖，而与其竞争的同科考生群体又在必考科目上表现较差，他就像一个在全球都算得上是富豪的人去到一个穷国一样，显得更加富有。

还有一个相反的问题就是：一个很差的考生，在一个最出色的选考科目群体中会不会占便宜?这是有可能的。一个最差的考生，在所有的选考科目都是垫底的话，这时他如果在最出色的选考科目群体中垫底是比较合算的。就像一个最穷的人，与其在一个穷国当穷人，不如在一个富国当穷人。不过，这样的考生，不管他选考什么都改变不了会落榜的结果。

当然，人们总可以举出一些特定的个案，认为用必考科目成绩校准选考科目成绩时或多或少会吃亏，但这种选考科目校准方法的关键在于，它对各科公平。必考科目是每位考生都要考的，用必考科目作为校准的依据，对每一个选考科目的考生而言都是比较公平的。

四、结语

新高考中的选考科目定级计分方法，第一批的两个省（市）在实施一次后就需要推出“保底”措施。以山东为代表的第二批试点省份在同一等级上做分数细化计分，但还是在把各选考科目难度摆平的同时也抹平了不同选考科目考生的整体能力差异，没有解决根本问题。与第一批试点省份一样，第二批试点改革对物理科考生不利。

以江苏省为代表的第三批试点省份，要求物理和历史必选一科。如果大学在招生的时候没有交叉录取，那就没有问题，否则这两科也存在分数比较的问题。因为，直接使用原始分有可能对物理科考生更加不利。至于其余四科（化学、生物、政治、地理）由于是自由选考，如果还是使用比例等级制计分的话，对差生及少人去选的科目比较不利，并且会恶性循环。

新高考改革从第一批试点到第三批试点所采用的选考科目定级计分方法表明，前一批的方法有问题，而后一批出现的问题也亟待规避和解决。一个问题解决了，另一个问题又来了：在用简单的方法摆平选考科目难度的同时，也抹平了选考科目考生整体能力实际上存在的差异。

选考科目考生群体能力是动态变化的，不同科目考生群体之间是存在差异的，而这种差异在不同年份之间也会发生变化。如果不将上述差异和变化考虑在内的任何定级计分方法，都注定会有问题。例如，发现某科考生吃亏了，就将其分数提高（提高平均分），虽然有可能会吸引更多差生去选考，但下一年该科考生的整体能力就下降了，因此继续按上一年方法来处理就会有问题。根据必考科目成绩校准选考科目成绩的方法，依据的是每一年每一科选考群体的必考科目成绩，因此能够同时考虑到上述的差异和变化，可以系统性地解决问题。

严格来说，不同的选考科目成绩不好比较。如果不需要合成高考总分，只需分别报告各科成绩，然后由高校根据各科成绩去招生，那么对选考科目成绩不进行校准，问题也不大。但既然要合成高考总分，相当于要比较选考科目成绩，那么用必考科目成绩做参照去校准选考科目成绩是比较合理的。它虽然不是最好的方法，但却是经实践检验过的可行的方法。此外，我们还可以结合基于课程标准的专家校准，做出比较合理的选考科目计分方案。