寻找“最佳证据”：如何运用元分析进行文献综述 ＊——以STEM 教育对学生成绩的影响研究为例

曾昭炳 姚继军

（南京师范大学教育科学学院，南京 210097）

一、教育循证研究的有效途径：从既有研究的综述中获得“最佳证据”

文献综述是对既往研究文献的梳理和概括。对于一项规范的学术研究而言，对文献进行“再研究”都是必不可少的环节。通过撰写文献综述，研究者可以充分了解所关注领域的研究进展，发现既有研究的不足，确定新的研究思路和研究问题，阐明本研究的缘由和意义，并在理论基础、变量设置、研究内容和研究方法等方面为新的研究提供依据（Denney，2013）。从这个角度而言，文献综述为所有类型的研究所必需。

就当下的教育研究现状而言，实证研究往往对文献综述更为重视。大多数规范的实证研究，都会基于对既往文献的梳理，提出研究的问题和假设，给出变量及方法选取的依据。但在文献综述的方法方面，目前大多数研究均采用传统的文献回顾和评述方法，所得结论更多地依赖于评述者的个人经验和主观判断，往往难以令人信服。姚计海（2017）认为，教育研究方法应具有科学性、系统性和独特性，按此标准，描述性文献综述并不能被当作独立的研究方法使用，其结论也不具有客观性、可验证性和可重复性，难以消除读者的质疑。

相对于实证研究，当下思辨研究的文献综述质量则受到了更多的批评。有研究在分析了我国教育学博士学位论文的文献综述后认为，目前大多数博士论文皆为思辨研究，其文献综述存在着堆砌材料、来源单一、缺少实质性分析、未能对既往研究进行充分概括与分析、写作不够规范等问题（张斌贤，李曙光，2015）。在这种情况下，文献综述根本无法为研究提供扎实的依据，有些研究者甚至出于便于论述或发表的目的，对文献进行筛选，选择有利于自己观点的文献而非具有重要学术价值的文献进行呈现，这就使得文献综述丧失了为研究提供依据的功能，从而变成了一个“任人打扮的小姑娘”。

这种情况正如教育循证研究（evidence-based educational research）代表人物、约翰霍普金斯大学Slavin 教授所批评的那样，“进入新世纪的教育实践仍处于前科学阶段（pre-scientific point），很多研究和决策缺少严谨、科学的评估证据，无法为儿童提供最好的教育项目，也无法推动教育的创新”（Slavin，2008）。而要解决这一问题，就需将“有效的证据作为选择教育产品和服务的主要标准”，这样才能让所实施的教育项目为儿童带来更好的发展，进而使教育进入创新、评估和渐进式改革的良性循环（Slavin，2017）。但问题在于，教育学这样的社会科学领域存在着大量的不可控因素，即便是严格控制了相关变量的实验研究及准实验研究，同类研究的结果也会不同。因此，人们需要一种科学严谨的方法对现有研究结果进行综合分析，以得出一个“最佳证据”来支持教育决策。这样的“最佳证据”，至少应满足以下条件：首先，它需按一定的标准，对既往研究成果做无偏的、全面的总结，不能因个人好恶或论证方便，对研究结果进行有目的地筛选和“控制”；其次，它需运用可比较的指标，分析不同的研究成果，并明确告诉人们，某项干预是否真的有效，以及有哪些因素会影响到这些外生变量的实施效果；再次，这样的证据应能经受并通过严格的稳健性检验，其结论具有一致性和可重复性。元分析作为一种定量与定性相结合的文献分析方法，能对既有实证文献进行较好的综合分析，或是寻求“最佳证据”的一种有效手段。

元分析最早由Glass 提出并应用于临床心理学，其基本思路是通过一定的标准对某一领域内的文献进行检索和筛选，对结果进行标准化处理后，通过加权平均得出一个综合性结论，并利用一定的统计方法探讨异质性的来源。元分析因能较好控制不同研究间的差异性并使其具有可比性而受到了研究者们的广泛重视和应用，与传统的、描述性的文献综述相比，元分析具有两个突出的优势：一是可相对科学地给出综合性的结论以解决研究争议，并能有效探索不同研究结果存在差异的原因；二是可对既有文献中的数据进行二次分析，使人们无需获得直接研究数据便可对某一领域的研究结果进行讨论（Borenstein et al.，2009，p. 9-13）。元分析虽不排斥评价者自身的研究经验，但由于有着较为严格的规范和要求，其结论会更为稳健与科学。因此，元分析迅速成为循证研究的主要方法之一。新世纪以来，随着教育循证改革的推进，使用元分析方法的研究数量迅速攀升。此类研究，不但对前期研究结论做了很好的总结，还能通过“异质性分析”等手段清晰地告诉人们，导致研究结论差异的因素是什么，这无疑对后续的实证研究和实践探索具有导向与启示作用。

与西方相比，我国高品质的教育实证研究成果还不够丰富，对既有实证研究成果的归纳与总结也比较欠缺。以本文探讨的STEM 教育为例，目前国内研究对这一舶来品的讨论大多停留在概念讨论和经验介绍阶段，相关实证研究几为空白，以致难以回答实践工作者迫切需要了解的一些问题：这一教育模式对学生发展是否有效?如果有效，哪些因素是其见效的关键?哪些STEM 教育方法可能取得更好的效果?等等。考虑到国外的相关研究早已展开，运用元分析技术对国外STEM 教育实证研究进行梳理，应可为国内STEM 教育的科学推进提供高价值的证据。本文下面的内容，即着眼于此，以STEM 教育对中小学生学习成绩的影响为切入点，运用元分析对国外相关实证研究结论进行定量整合，力图为中国的STEM 教育改革提供可靠的研究证据。

二、文献回顾与问题提出

以1986 年美国国家科学委员会（NSB）发布的《本科科学、数学和工程教育》（Undergraduate Science Mathematics and Engineering Education）为标志，STEM 教育迅速成为国际教育界普遍关注的热点问题。成绩作为衡量教育质量的一个重要指标，STEM 教育是否有助于提高学生成绩，进而是否有利于提高人才培养质量，便成为人们最为关注的问题之一。

如前所述，以美国为代表的一些国家（或地区）在STEM 教育评估领域已积累了一定的实证研究成果，但这部分研究对STEM 教育效果的认识未达成一致。有学者发现接受STEM 教育的学生在测试中的表现要远远好于未接受STEM 教育的学生，比如Cakici & Turkemen（2013）发现，在前测差异不显著的情况下，STEM 教育组学生的科学测试成绩远高于非STEM 教育组的学生，效应量高达2.404；类似的研究还有Kassir（2013）、Robinson 等（2014）、Rehmat（2015）、Acar 等（2018），都发现STEM 教育对学生科学成绩的提升有很大帮助，效应量分别为1.781、1.902、0.940 和1.247。也有些研究发现，接受STEM 教育的学生，其成绩只在较小或中等程度上有所提升。比如Korur 等（2015）发现基于设计的学习（design-based learning）帮助学生提高科学成绩的效果为0.728；Cervetti（2012）的研究结果表明采用STEM 整合教育模式后，可在中等程度上提高学生的科学成绩（ES=0.501）；Olivarez（2013）使用因果比较研究分析了STEM 教育组与非STEM 教育组的学生在数学、阅读测试中的表现，发现STEM 教育组的学生优于非STEM 教育组，效应量分别为0.649 和0.549；Harris 等（2015）以及Han 等（2016）的研究则表明在提升学生测试表现上，STEM 教育相比非STEM 教育只具有微弱的优势，效应量分别为0.220 和0.170。上述研究虽然在STEM 教育效果的大小方面观点不一，但至少说明STEM 教育更有利于提高学生的学业成绩。有些学者则与上述学者的观点完全相反，他们发现STEM 教育在提升学生成绩方面并不比传统教育更为有效，甚至存在负效应。比如Merill（2001）、Li 等（2016）的研究表明STEM 教育对学生学业成绩几乎没有影响，效应量接近为0（d=0.026、d=0.015）；Barth（2013）、James（2014）的研究则表明STEM 教育不利于提高学生的学业成绩，其效应量分别为-0.147 和-0.412。

由此可见，有关STEM 教育效果的实证研究并未得出统一的结论，这意味着STEM 教育对学生成绩的影响，或受多种因素影响并有着较为复杂的影响机制。正如Glass 当年试图用元分析方法回应“心理疗法是否有效”这一争议一样，目前已有学者试图通过元分析来解决“STEM 教育是否有效”这个问题中存在的分歧，并探讨造成研究差异的原因。相关研究的大致信息如表1 所示。

表1 STEM 教育领域内元分析研究的基本信息

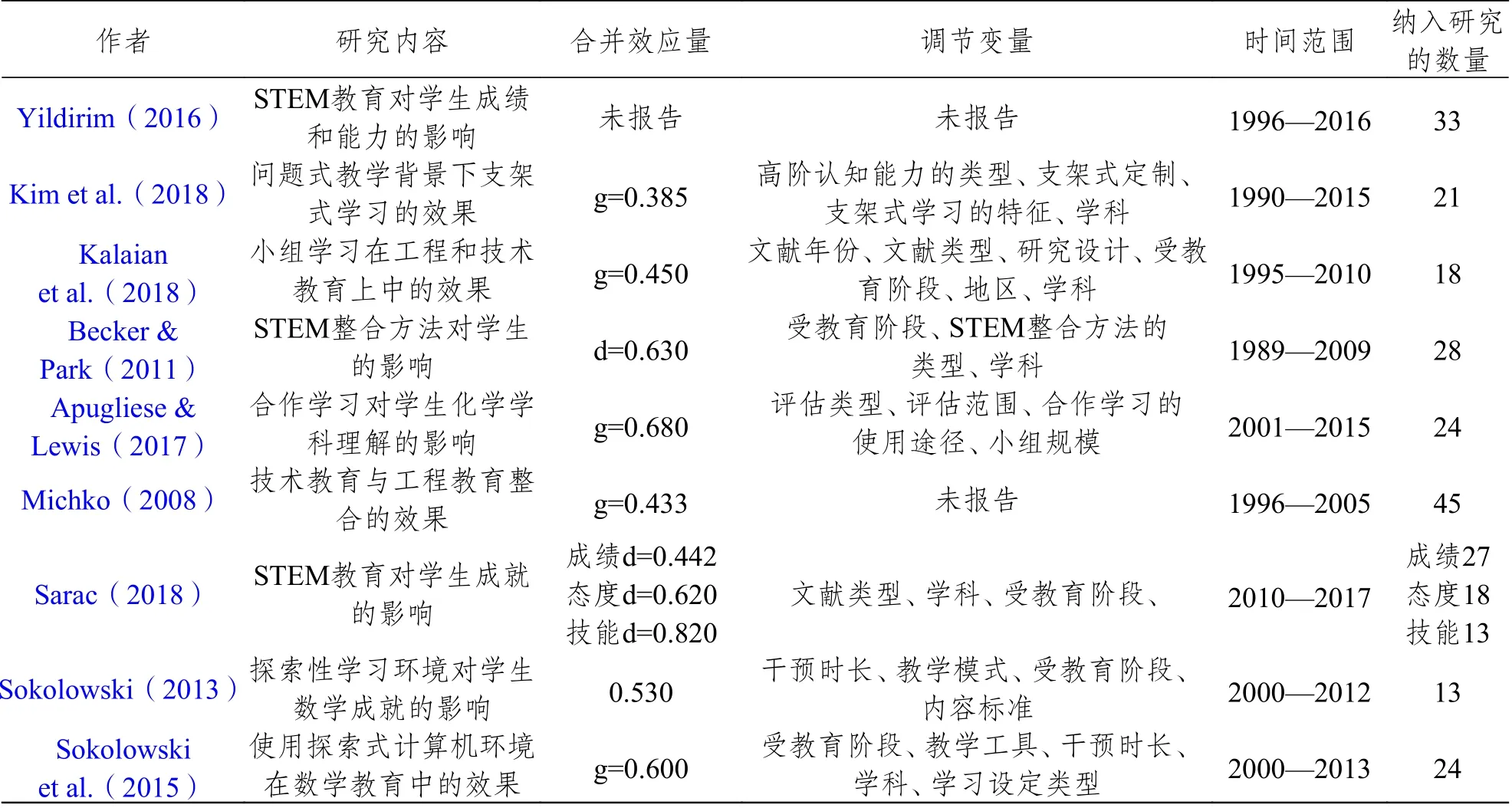
续表1

从表1 中可以看出，既有的元分析研究大多探讨某一方法在STEM 学科教育中的教学效果，此类研究约占九成。仅有Yildirim（2016）、Sarac（2018）从整体上探讨STEM 教育对学生学业成绩、能力或态度的影响。但是他们的研究仍有许多可以改进的地方。比如Yildirim 只对相关实证研究进行了系统性综述，未计算效应量从而无法直观、具体地判断STEM 教育对学生成绩和能力的影响。Sarac 的研究虽然计算了合并效应量，比较全面地测算了STEM 教育的效果（对学生成绩、态度和能力的影响的合并效应量分别为0.442、0.620 和0.820）；但是他对STEM 教育概念的界定过于宽泛，没有给出筛选文献的标准，未对纳入的文献进行质量评估，异质性分析也不够详细。这表明，尽管元分析是解决本领域实证研究差异的重要手段，但到目前为止，规范的、高质量的元分析仍较为缺乏。这在一定程度上影响了人们对STEM 教育规律的认识。

近年来，中国开始尝试推进STEM 教育，但人们对于STEM 教育效果的认识还基本停留在理论和经验层面。因此对国外本领域的实证研究结果进行归纳和总结，将在规律层面为我国的STEM 教育事业发展提供科学证据。有鉴于此，本研究将运用严谨而规范的元分析方法，讨论国外的实证研究结论，以帮助我国的研究者和实践工作者，了解STEM 教育对学生成绩影响的一般规律，推进我国STEM 教育的发展。为此，本研究将重点回答以下三个问题：

1. 相比于非STEM 教育，STEM 教育是否有利于提高学生成绩?

2. 若STEM 教育对学生的成绩有影响，影响程度有多大?

3. 哪些因素会影响到STEM 教育的效果?

三、概念界定与研究步骤

（一）核心概念的界定

在元分析的过程中，首先要做的工作就是对核心概念进行界定。这是因为只有确定了核心概念（或研究对象）的“操作性”定义后，才可能框定文献检索和筛选的范围。到目前为止，人们对“STEM教育”这个概念并未形成完全统一的认识。Carmichael（2017）通过分析政策文本，发现美国各州在实施STEM 教育的过程中，对STEM 教育的理解和期望都存有差异。因此，我们将通过简单回顾STEM 教育的发展历程，来把握其核心内涵并合理界定概念。事实上，在STEM 这个缩写刚被提出时，它所指的只是科学、技术、工程和数学四门学科及相关领域。早期的STEM 教育更多地聚焦于学科领域的知识，并常常单独教授STEM 的学科内容，这往往使得学生缺乏对STEM 学科的兴趣，学业表现也差强人意（Atkinson & Mayo，2010；Kelley & Knowles，2016）。因此美国提出了一系列改进STEM 教育质量的措施，其中就包括实行STEM 整合教育（integrated STEM education），并将学科间的整合从STEM 学科扩大到其他领域，强调基于真实情境与问题的教学（Honey，et al.，2014；Macdonald，2016）。在此过程中，以真实情景、学科融合、问题解决及学生中心为特征的STEM 教育模式逐步得到了广泛认可。基于此，我们将“STEM 教育”界定为：在真实情境中，利用项目式学习、问题式学习等以学生为中心的学习方式有机整合科学、技术、工程、数学或更多学科的一种教育。本文将按此定义框定文献范围并筛选符合要求的文献。

（二）研究步骤

本文按照元分析的一般步骤展开：第一，在理论分析和概念界定的基础上，确定文献搜索的范围和纳入标准，进而在各类数据库中检索相关文献，形成分析所需数据；第二，对所纳入的文献进行编码，列出纳入文献的详细统计信息，并对所纳入文献的质量进行评估；第三，计算合并效应量，分析STEM 教育对学习成绩影响的整体程度，回答本研究的第一和第二个问题，并在此基础上，进行异质性分析以讨论STEM 教育影响学生成绩的因素和机制，回答本研究的第三个问题；第四，进行稳健性检验，通过检验、校正发表偏倚与敏感性分析，确保结果的可靠性和科学性。以上步骤中涉及的数据分析工作均通过Comprehensive Meta-Analysis 2.0 软件来完成。

四、文献检索与质量评估

（一）文献纳入标准

元分析在确定文献纳入标准的过程中要尽量排除研究者的个人偏好，更多地依据研究目的、研究内容、文献特征和统计要求来确定。比如Lipsey & Wilson（2001，p. 16-20）指出，文献纳入标准需至少包含以下几个基本要素：需纳入文献的显著特征、研究对象、关键变量、研究设计、文化和语言范围、时间范围、文献类型。结合研究目的以及纳入标准应包含的基本要素，本研究拟定了以下七条标准用以筛选文献：

1. 研究所使用的语言为英语，发表于1996—2018 年间，文献类型不限。

2. 研究内容为STEM 教育对基础教育阶段学生测试成绩的影响，不包括特殊教育、职业教育及校外STEM 项目（out-school program）。

3. 研究设计为实验设计，对比STEM 教育与非STEM 教育效果的差异。参照Cheung & Slavin（2013a）的标准，文章需报告前测结果，差异过大的研究将被排除（ES>0.5），随机实验可不进行前测。

4. 至少由两名老师分别对实验组和控制组进行教学，尽量减少教师因素所带来的影响。若两组只由一名老师进行教学，无法保证干预措施的独立性，或会影响实验结果。

5. 研究在实验的进程中，不应告知学生研究的目的。因为在告知学生研究目的的情况下可能会导致实验结果出现偏差。

6. 实验组与对照组的样本量应相近。若实验组与对照组有一组样本量过小，且两者之间差距过大，可能导致研究结果存在偏误。

7. 研究应报告均值、标准差、样本量或t 值、F 值等统计信息，确保能够计算出效应量。

（二）文献的检索与筛选

所谓“最佳证据”应当是更具代表性和全面性的证据，其来源应当尽可能地广泛，不遗漏任何有价值的研究。为此，本研究以“STEM education”、“integrated STEM education”、“student achievement”等关键词在教育数据库以及搜索引擎（e.g.，ERIC，EBSCO，Springer，Google Scholar）中进行检索。根据已制定的纳入标准，先是对文献标题进行筛选，排除明显不符合标准的研究，并将可能符合标准的文献下载存档；然后阅读文献摘要，进一步排除不符合要求的研究；最后对剩余的文献进行全文阅读，筛选出完全符合标准的文献。本研究共检索了28683 篇文献，最终纳入17 篇，获得20 个效应量。文献检索与筛选流程如图1 所示。

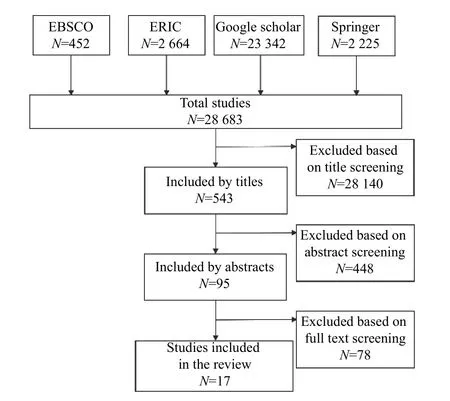
图1 文献检索与筛选流程

（三）文献编码

获得可供分析的文献后，需要将文献进行编码以便于信息提取与数据分析。本研究使用的编码规则如下：

1. 性别（Ge）：女编码为F，男编码为M，男女都有编码为B，未报告样本性别信息的编码为U。

2. 家庭社会经济地位（SES）：低SES 编码为L，中SES 编码为M，高SES 编码为H，样本低、中、高SES 都有编码为V，未报告SES 编码为U。

3. 种族（E）：白人编码为W，非裔编码为B，亚裔编码为A，西班牙裔编码为H，其他编码为O，样本中包含多个种族编码为V，未报告种族信息编码为U。

4. 受教育阶段（Gr）：K—5 年级编码为P，6—8 年级编码为M，9—12 年级编码为H。由于各地区学制不同，具体编码以作者报告为准。

5. 学科（D）：科学编码为science，数学编码为mathematics，工程编码为engineering。

6. 地区（L）：以作者报告的地区名称作为编码。

7. STEM 教育方法（I）：项目式学习（project-based learning）编码为PBL，问题式学习（problem-based learning）编码为pbl，探究式学习编码为（inquiry-based learning）IBL，其他以作者所报告STEM 教育措施为编码。

8. 研究设计（Rd）：准实验设计编码为QE，随机实验设计编码为RE。

9. 样本量（Ss）：大样本编码为L，小样本编码为S。参照Cheung & Slavin（2013b），样本量大于250 的为大样本，小于等于250 的为小样本。

10. 测试工具类型（Ti）：标准化测试工具编码为1，非标准化测试工具编码为0（研究中将大型测试或依据学科标准制定的测试题视为标准化测试，其余视为非标准化测试）。

11. 文献发表年份（Py）：分阶段编码为1996—2007 或2007—NOW。根据Sanders（2009），上世纪90 年代中期首次提出“STEM”这个缩写；2007 年首次提出“STEM 教育整合”，强调学科之间的有机融合。

12. 文献类型（Lt）：期刊编码为（J），非期刊类编码为（non-J）。

已纳入文献的部分信息如表2 所示。

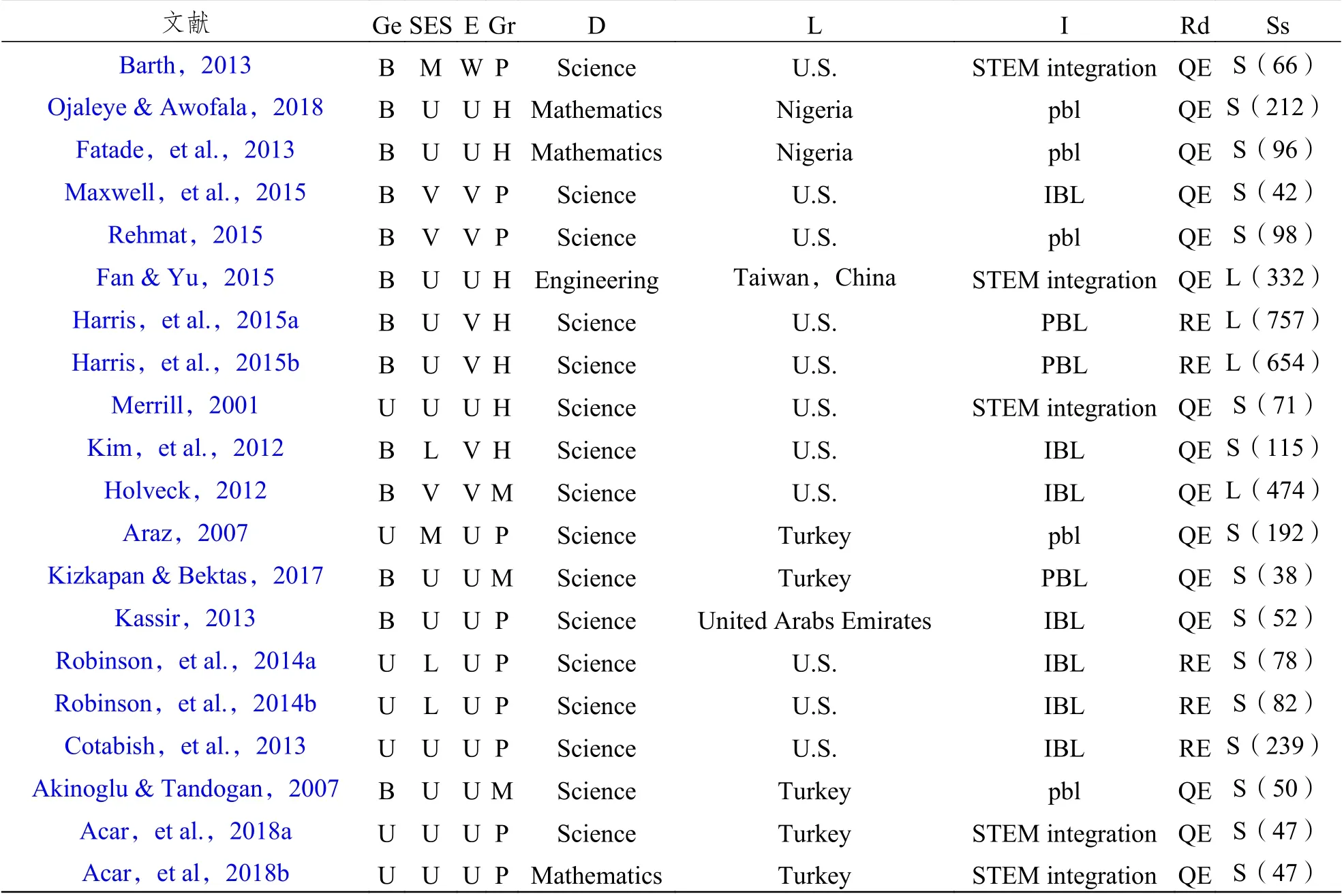
表2 纳入文献的信息

（四）文献质量评估

在元分析过程中，所纳入文献的质量会影响到最终结果的质量。我们参照Valentine & Cooper（2003）评估文献质量的方法，从纳入文献是否清楚地描述了干预措施、研究设计、样本特征、测试工具以及测量过程等五个方面对文献质量打分，其中，“不清楚”赋值为1，“较清楚”赋值为2，“清楚”赋值为3。一篇文献可获得的最高分为15 分，得分越高质量越高。为确保文献质量的评价尽可能客观，这一过程由本文的第一作者与通讯作者（姚继军）独立进行，各文献得分分值范围为7—13 分，评分一致性为0.910（p<0.0001），纳入文献的质量基本满足分析需求。

五、计算合并效应量与异质性分析

（一）STEM 教育对学生成绩影响的合并效应量

计算合并效应量是元分析的核心工作。这是因为，传统的虚无假设显著性检验（null hypothesis significance testing，NHST）仅能给出结果显著与否的结论，但却无法在不同样本数量的研究中比较结果的有效性。从寻找“最佳证据”的角度而言，如果我们得到的证据无法确切地给出某项干预措施的效果大小，且无法比较不同干预措施之间的优劣，那么这样的证据也就无法准确判断相关教育改革（干预）的效果并给出未来改进的方向。效应量指标恰恰可以解决这个问题，Chow（1988）认为，效应量不但能指出自变量作用的大小，而且可作为统一的度量标准用以比较包含相同变量的系列实验的结果；更为重要的是，人们可以通过元分析等技术手段，对效应量进行平均以给出某一方面研究的一般性结论。

然而，不同文献的研究设计不同，所使用的数据类型也有所差别。因此需要针对不同的数据和研究设计选择合适的效应量，必要的时候还需要进行效应量之间的转换（卢谢峰等，2011；Borenstein et al.，2009，p. 45-49）。具体到本研究，由于学生成绩为连续性变量，纳入的文献皆为实验设计并比较组间差异，因此笔者选用Cohen’s d 作为效应量。计算合并效应量的具体步骤是：

1. 计算各文献的效应量。

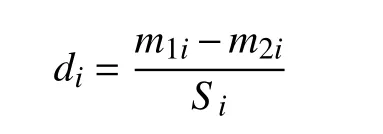
其中si为合并标准差，m1i为实验组均值，m2i为对照组均值。

2. 采用逆方差加权（inverse variance weighting）对各效应量进行赋权。

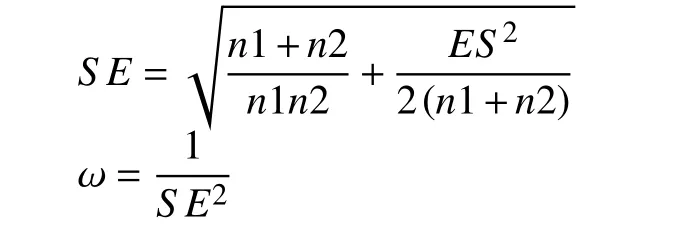
3. 通过加权平均计算合并效应量。

经Q 检验，发现研究间存在异质性（Q=168.11，p < 0.0001），且我们假设除样本误差外，还有其他因素导致了各研究结果存在差异，因此采用随机效应模型（random-effect model）（Borenstein et al.，2009，p.83）进行分析，详细结果如表3 所示。

各文献的效应量分布在（-0.147，1.902）之间。参照Cohen（1988）的标准，0.2 为小效应，0.5 为中等效应，0.8 为大效应。所纳入文献中，报告了大效应的有8 篇，且都具有统计意义，其中3 篇文献报告的效应量超过了1。效应量最大的是Robinson 等（2014）的研究，第一年测得的效应量为1.902（p<0.0001），第二年测得的效应量为1.713（p<0.0001）；Kassir（2013）的结果与Robinson 相近，效应量为1.781；Acar（2018）则发现STEM 教育对科学和数学成绩的提高程度都比较大，效应量分别为1.247 和1.174。报告了中等效应的有2 篇，且都比较接近于大效应量，其大小分别为0.789 和0.693。其余文献所报告的为小效应、负效应或不具统计意义。通过计算，未经发表偏倚矫正和稳健性检验的合并效应量为0.700（p<0.0001），是一个中等大小的效应量。

（二）异质性分析

元分析的另一项核心工作是异质性分析。在寻找“最佳证据”的过程中，我们不仅需要了解某项干预的综合效应，还需要知道有哪些因素会对干预的结果产生影响。元分析可以通过异质性分析，来对影响研究结论的因素进行讨论。调节变量分析（moderator analysis）是进行异质性分析的主要方法之一，根据一定的特征划分亚组，通过Q 检验比较各组之间是否存在差异，便可判断该特征是不是导致异质性的原因（Borenstein et al.，2009，p. 149-186）。调节变量的选取主要有两条途径。一是参照既有的元分析文献，或是探讨影响STEM 教育效果的因素的研究。对表1 中元分析文献所选定的调节变量进行简单的频数统计，出现频数超过3 次的调节变量有以下几个：受教育阶段（11 次），教学方法（6 次）、学科（8 次）、干预时长（5 次）、研究设计（7 次）、文献类型（3 次）、测试工具类型（3 次）、测试项目（3 次）、文献年份（3 次）。此外，还有学者表明STEM 教育的效果或受学生的性别、家庭社会经济地位（SES）以及种族等因素的影响。比如Bicer 等（2015）发现接受STEM 教育的女同学比未接受STEM 教育的男同学的成绩要好，STEM 教育组中低SES 的学生要比非STEM 教育组中高SES 的学生在数学上表现更好；Rozek 等人（2019）表明低SES 的学生在学习STEM 课程时更为吃力。诸如此类的研究都可以作为选择调节变量的参考。二是从专业角度及统计学角度来选取，比如张天嵩等（2015，第312 页）认为可从设计方案、研究质量等角度选取划分亚组的因素。结合以上两条选取调节变量的途径及本文的研究目的，笔者从研究特征、干预特征及文献特征三个方面选取调节变量，具体如表4 所示。

表4 调节变量的选取及其分类

由于已纳入的文献所报告的样本特征信息不足，加之本研究只探讨STEM 教育对学生学业成绩的影响，因此样本特征和测试项目不纳入调节变量分析之中。其余调节变量的分析结果如表5 所示。

由表5 可知，STEM 教育方法、受教育阶段、地区以及样本量的不同都是造成各研究效应量存在差异的原因：

1. 就STEM 教育方法而言（QB=47.760，p<0.0001），效果最好的是探究式学习（d=0.907），其次是问题式学习（d=0.888），二者都是大效应；学科整合则在中等程度上有利于提高学生的成绩（d=0.614）；项目式学习在提升学生成绩方面的效应量为0.228，是一个小效应量。

2. 就受教育阶段而言（QB=8.287，p=0.016），小学阶段STEM 教育效果最好（d=1.021），高中阶段其次（d=0.487），初中阶段STEM 教育效果较为一般（d=0.237）且不显著。

3. 就地区而言（QB=14.022，p=0.007），中国台湾、尼日利亚、土耳其以及阿拉伯联合酋长国STEM 教育的效果比较好，效应量分别为0.862、0.880、0.834 和1.781；而作为STEM 教育起源地的美国，纳入的文献最多，效应量相对较小（d=0.515），但也是一个中等效应量。

4. 就样本量而言（QB=5.782，p=0.016），大样本研究的效应量较小，为0.333；小样本研究的效应量则比较大，为0.816。

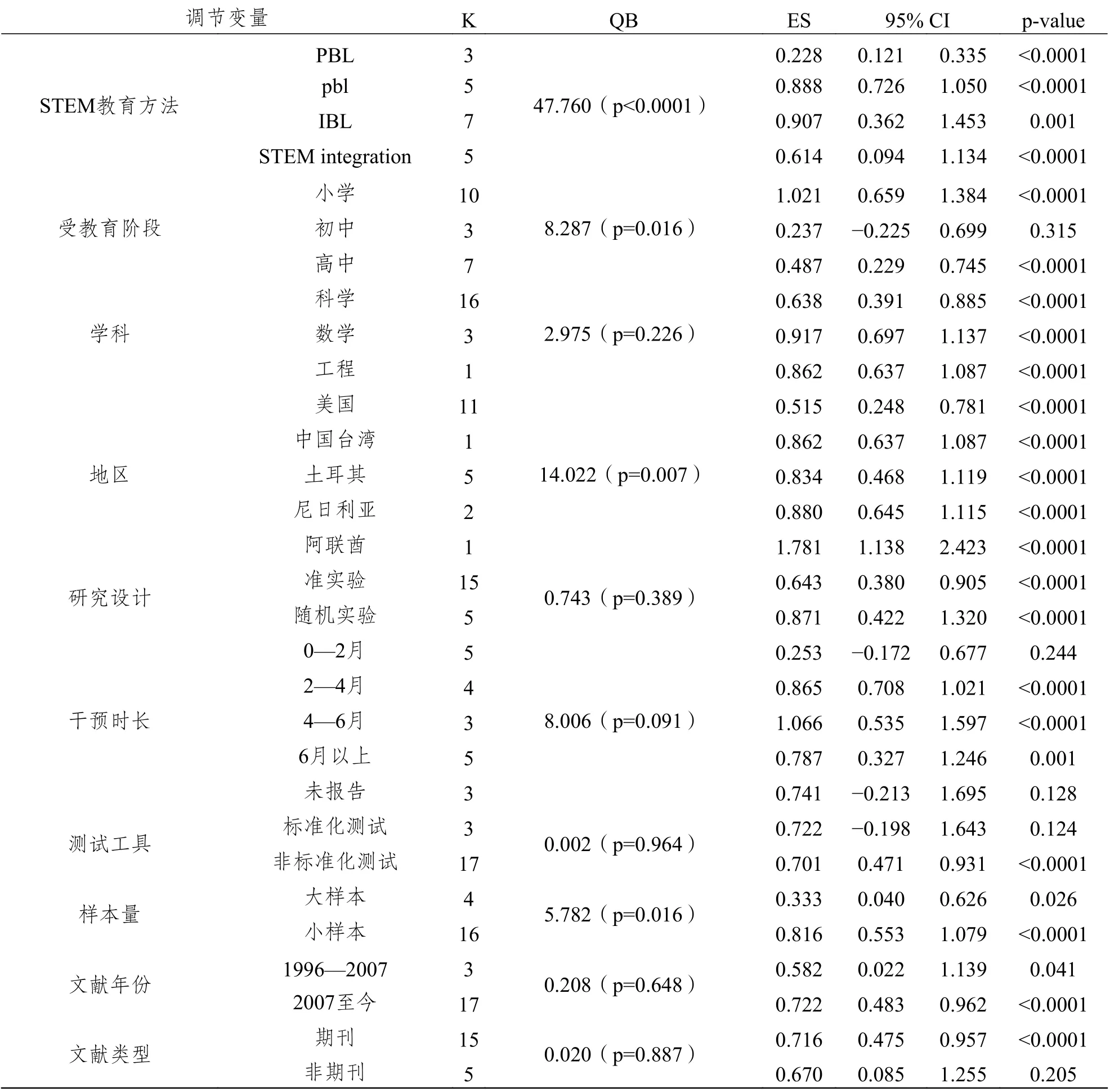
表5 调节效应分析

六、分析结果的稳健性检验

（一）发表偏倚的检验与效应量调整

一般而言，发表偏倚是指统计结果为正向显著的研究成果，更容易被期刊所接受并发表的一种现象。如果存在发表偏倚，元分析的结果可能会面临放大干预措施真实效果的风险（Rothstein et al.，2005，p. 2-3）。发表偏倚是影响研究结果可靠性的一个重要因素，因此对其进行检验是元分析不可或缺的重要一环。常用的检验方法是漏斗图，通过观察漏斗图是否对称来判断发表偏倚存在与否；若无法直观判断出漏斗图是否对称，则可通过Egger 检验来确定。本研究的漏斗图如图2 所示，该图明显不对称，Egger 检验的结果也显著（B0=3.289，t=2.714，p1=0.007，p2=0.014），这表明本研究存在发表偏倚。发表偏倚作为一种不可控的因素，元分析的研究者很难完全避免这一问题。若存在发表偏倚，则需要对发表偏倚进行修正并测算所缺失的研究文献对元分析结果的影响，同时还要更为谨慎地讨论研究的结果，以确保分析结果足够稳健。但需要指出的是，是否存在发表偏倚并不能作为评价元分析质量的唯一标准。事实上，无论是元分析还是传统的文献综述，都可能存在因发表偏倚而导致的“有偏估计”问题。相比于传统文献综述，元分析的研究者们已经发展出了一系列检验、修正发表偏倚的技术，以最大限度地保证分析结果的稳健性。

图2 发表偏倚检验（漏斗图）

修正与测算发表偏倚影响的常用方法是剪补法（trim and fill），其主要步骤是：首先，剪除（trim）引起漏斗图不对称的研究，并重新计算合并效应量（中心值）；其次，将去除的研究沿新的中心对称地填补（fill）到对称轴的另一侧；最后，计算合并效应量及其标准差，并不断叠代以上过程直至结果稳定（Duval & Tweedie，2000；Rothstein et al.，2005，p. 127-144）。Bediou 等人（2018）近期发表在心理学权威期刊《Psychology Bulletin》上的研究，便是利用这一方法修正了发表偏倚对研究结果的影响。参考以上研究，我们同样运用剪补法，对本文的效应量进行修正。修正后的合并效应量为0.410，95%置信区间为（0.185，0.636），说明发表偏倚的存在或导致效应量放大了41.43%。那么，这样一个经过修正的效应量是否可靠呢?为解决这个问题，我们还需要对结果进行敏感性检验，以评估元分析结果对发表偏倚的反应程度。

（二）敏感性分析

进行敏感性分析的常用方法是失安全系数法（failed-safe N）。通过对失安全系数的计算，我们可以判断因存在发表偏倚而逆转元分析结论的可能性（Cheung，& Slavin，2012；Lazowski，& Hulleman，2015）。该方法由Rosenthal（1979）提出，通过计算最少需要缺失多少研究才能使元分析的结论发生逆转，进而判断结论的稳健性。该系数值越大，说明虽然存在发表偏倚，但元分析结果对缺失文献的反应越不敏感。若新增研究个数小于5K+10 个（K 为纳入的文献数量），则对所得到的结论要慎重对待。本研究计算的Classic 失安全系数N=1257（α=0.050，p<0.0001），即需要额外纳入1257 篇文献，元分析的结论才能被推翻。

以上分析结果表明，本研究修正后的效应量，已经在一定程度上消除了发表偏倚对分析结果的影响，且研究结果较为稳健。这说明0.410 更为接近STEM 教育效果的真实效应量。

七、结论与讨论

经过严格的统计分析，我们可以得出结论：STEM 教育有利于提高学生的学业成绩，但是提升的程度较小（d=0.410）；诸如STEM 教育方法、受教育阶段、地区和样本量等都是造成实证研究结果不同的因素。本研究的结论支持“STEM 教育比传统教育模式更有利于提高学生的成绩”这一观点。对比同类研究，本文所得到的合并效应量略小于Sarac（2018）的0.442。但是Sarac 的研究除了前文提到的一些不足外，对发表偏倚的检验和讨论也有失严谨。因此，可认为本研究的结论更具稳健性。

本研究还进一步分析了造成各研究结果存在差异的原因。整体而言，这些原因可以分为两类。一类是研究设计本身引起的差异。比如，本研究发现，样本所在地区不同，STEM 教育的效果也不同。由于地区间文化存在差异，或可推测文化因素会影响STEM 教育的效果。就样本量而言，大样本研究的效应量远小于小样本研究，也更接近合并效应量。此外，虽然干预时长的异质性分析结果不显著，但是干预时长过短（0—2 月）的研究其平均效应量与其他亚组相比要小很多。可以推论要更为准确地评估STEM 教育的效果，应在条件允许的情况下，尽可能地增加样本量，并延长干预的时间，这样可减小研究结果的误差。

另一类导致结果不同的原因可归结为STEM 教育本身的特征。对这类原因的分析，将有助于我们了解，到底什么样的STEM 教育对学生的学习结果作用更为明显。具体而言，在STEM 教育方法方面，本研究表明不同的教育方法在提升学生学业成绩的表现上有所差别。比如学科整合方法在中等程度上有利于学生学业成绩的提升（d=0.614），这一结果与Becker & Park（2011）所得的结论非常接近（d=0.630）；问题式学习又比学科整合的效果更好，是一个大效应量（d=0.888）；项目式学习在提高学生成绩方面的效应量最小。既有研究表明，一些学习方法在促进学生能力发展方面的作用或远大于其在提高学生成绩方面的作用。以项目式学习为例，本研究表明其提高学生的成绩的效应量仅为0.228，Zeng 等人（2018）的研究却发现，这一方法对学生能力的提升作用非常明显，效应量高达1.335。就学科内容而言，本研究发现使用同一STEM 教育方法教授不同的内容，其效果差异并不显著，这也从一定程度上反映了STEM 学科之间具有紧密的内在联系（Bicer，et al.，2017）。就学生的受教育阶段而言，STEM 教育似乎最适合于在小学阶段实施，高中阶段实施STEM 教育的效果则一般，初中阶段的效应量最小，仅为0.237 且不具统计意义。已有研究表明STEM 教育的效果或受学生学习经验的影响，刚接触STEM 教育的学生其表现要好于接触过STEM 教育的学生（Taylor，2016），但这无法解释为何STEM 教育在初中阶段表现一般，其中的机制仍有待进一步揭示。

受纳入文献信息所限，本研究无法通过调节变量分析来判断样本特征（性别、SES、种族）是否会影响STEM 教育的效果，但已有研究指出，不同性别的学生在空间能力（spacial ability）上存在差异，进而影响STEM 学习表现，但这种能力上的差异是可塑的（Kine，2017）；还有研究发现家庭社会经济地位也会影响学生学习STEM 的效果（Bicer，et al.，2015；Rozek，et al.，2019）。

综合来看，STEM 教育虽然比传统教育模式更有利于学生的发展，但其作用机制仍是一个黑箱，打开这个黑箱是今后STEM 教育研究的一个重点方向。

八、结语

回到本文最初探讨的问题：如何基于既往教育研究文献为教育的改革与发展提供“最佳证据”?本研究可被视为是一个方法上的探索。与传统的主观性文献综述相比，本文的研究过程表明，规范的元分析至少具有以下几个方面的优势：第一，由于在文献搜集前，必须要确定“操作性定义”，因此元分析要求对核心概念进行严谨的界定，这就避免了概念含混不清的问题。第二，元分析有着明确的文献检索和纳入标准，这就解决了过度依赖个人经验甚至主观好恶选择文献的问题。虽然元分析在确定文献纳入标准时，也会受研究者个人研究背景和经验的影响，但这样的影响最终仍要以确定性的标准来体现，而非像有些主观性文献综述那样，可将文献筛选的标准“隐藏”于作者的意图之后，进而根据预设观点去安排文献。第三，在技术层面，元分析有着更为严谨的检验流程，可通过漏斗图、失安全系数等定量分析手段，更好地确保分析结果的稳健性。第四，与以上几点相关，元分析具有可重复性和可验证性。在研究对象、核心概念界定、文献筛选标准一致的情况下，不同的研究者使用元分析方法可以得到相同或相近的结论，这是传统的主观性文献综述所不具备的优势。需要指出的是，元分析到目前为止，主要还是用于对实证研究文献的分析，难以分析思辨研究文献。这可以视为这一方法的局限之一。但这并不意味着，基于元分析的结论不能为思辨研究提供证据。相对于传统的主观性文献综述，通过元分析方法对既有研究文献进行科学的梳理和综合归纳，所得到的证据，无疑更具一般性和指导性，更符合“最佳证据”的要求。这样的证据，无论对哪一类研究而言，都具有更强的证据效力，从而帮助相关研究建立在更为扎实的基础之上。

毋庸讳言的是，由于聚焦国内教育问题的高水准实证研究，尤其是严格设计的实验研究还较为缺乏，当前开展教育领域的元分析，在国内文献来源方面存在着一定的困难。为此，一方面，要大力强化和推动国内的教育实验研究。这是因为国内大多数实证研究均为相关性分析，这虽能帮助人们认识特定教育现象的影响因素，但却难以进行因果推断。而在不设对照组的教育实证研究中，还存在着有偏估计干预效果的风险（Cheung & Slavin，2016）。要解决这一问题，从技术上来说，最好的方式便是开展严格设计的实验研究。这样，人们才能在更多的实证研究的基础之上，通过元分析等技术获得一般性的结论。另一方面，要倡导文献综述研究的“证据”意识。当前的教育类综述研究很多都存在着评述不全面、过程不严谨、结论不可靠等问题。我们无意否定主观性文献综述研究的价值，并坚信高品质的综述研究，无论是否使用元分析方法，都会推进教育的研究与实践的进步。但如前所述，从理论研究与实践工作的关系而言，主要聚焦于学理探究和观点表达的主观性文献综述，很难为实践工作提供直接的、有效的、稳健的“最佳证据”。从这个角度而言，本文所展示的方法，或为丰富教育文献综述研究，更好地服务教育实践探索提供了一条有效路径。