数学教材中数学文化研究
——以青岛版《最美的图形——圆》单元为例
2020-06-23山东教育科学研究院徐云鸿
山东教育科学研究院 徐云鸿
山东济南市新苑小学 刘秀玲
《义务教育数学课程标准(2011年版)》在第一部分前言中明确指出:“数学是人类文化的重要组成部分,数学素养是现代社会每一个公民应该具备的基本素养。”数学作为人类文化的重要组成部分,对人的全面发展有着重大意义。数学文化,无论对激发学生的学习兴趣还是对培养学生的创新素养,“其内涵是宏阔而深邃的,其功效是坚固而持久的,其形态是不断生成而富有生机的。”教材作为教师教学的重要依据和资源,承担着向学生传递数学文化的重要功能。鉴于此,本文尝试对青岛版小学数学《最美的图形——圆》(以下简称为《圆》)单元的数学文化渗透情况进行分析解读,从数学文化类型、数学文化运用水平、数学文化的功能三个维度进行分析,试图解析教材是如何体现数学文化、包含了哪些数学文化以及是如何运用数学文化的,在此基础上对教材进一步加强数学文化提出建议,并为教师教学提供一定的参考。
一、《圆》单元数学文化的类型分析
从文化的高度来建设数学课程是青岛版教材的一大特色。教材力求通过各种文化素材浸润学生心灵,点燃学生求知的激情,感受数学的美妙与美好,增强数学应用和创新意识,进而促进学生核心素养的发展。
关于数学文化的类型,不同的学者有不同的理解,因而划分的角度也不尽相同。汪晓勤等将数学文化类型划分为:数学史、数学与生活、数学与科技、数学与人文艺术四个方面,本文将按照这种划分对《圆》单元进行分析。本单元共包括48项有关数学文化的项目,其中练习题之外的项目(记为C1)15项,练习题(记为C2)33项,见表1。
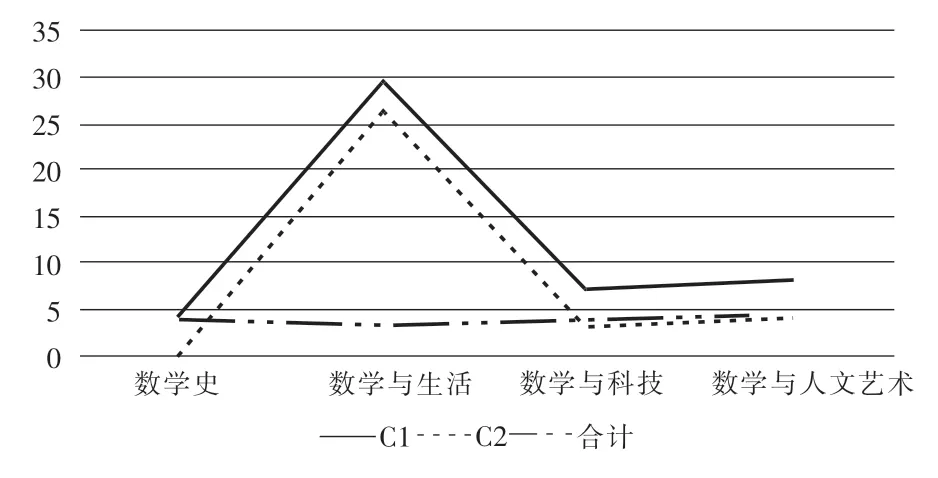
表1 《圆》一章中数学文化的类型
通过分析数学文化的类型,我们发现,青岛版数学教材所选择的素材内容较为广泛。其中,“数学与生活”的内容最多,体现了数学的应用价值;同时还设计了少量的“数学与人文艺术”的内容,体现了数学的人文价值;在C1和C2中均体现了“数学与科技”的融合。总之,数学文化类型涵盖了各个方面。当然,从具体类型而言,数学文化的类型还不太均衡,“数学与生活”占绝大多数,“数学与人文艺术”“数学与科技”的类型不足。因此,如何纳入更多的人文艺术类、科技类的文化素材需要进一步思考。具体分析如下:
(一)“数学史”的内容分析及教材改进建议
(1)数学史的内容分析。数学史是数学文化的一种载体,是教学中渗透数学文化的一种有效途径。将数学史的内容渗透到教材中可以让学生产生文化归属感。本单元以数学史为载体渗透数学文化的项目共4项,包括我国的数学成就(圆周率);圆的面积推导中引入了刘徽的“割圆术”和西方的“切西瓜”原理;数学家(介绍祖冲之),均出现在C1中,在C2中没有出现数学史方面的文化渗透,这与本单元知识点有关。
教材中对史料内容的选择传承了我国深厚的数学文化,既可以激发学生对数学的兴趣,又有利于培养学生的民族自豪感。
(2)教材中“数学史”编写的改进建议。建议进一步丰富与“圆”相关的数学史料。与圆相关的数学史料内容很多,教材应该为学生呈现出最经典、最核心的数学史料内容。在信息窗一“圆的认识”中可增加古代对圆的特征的记载。比如《墨子·经上》:“圜,一中同长也。”《孟子》中说“不以规矩,不能成方圆”后来演化成了用以指导人们生活的名言警句,《周髀算经》中“圆出于方、方出于矩”等。这些数学史资料无疑可以很好地帮助学生更加深刻地认识“圆”,揭示“圆”的知识背后隐藏的深厚文化底蕴,增加民族自豪感与自信心。青岛版教材在信息窗二仅介绍了《周髀算经》的相关记载,而不能忽略的是刘徽的割圆术,正是有了刘徽的贡献,才为后来圆周率的研究奠定了重要的基础。还有阿基米德等的研究成果,以及现代利用计算机技术对圆周率的研究进展等,如果在教材中增加这些内容,能够让学生更加完整地了解圆周率的研究史,体会数学发展历史的曲折,感悟数学家孜孜以求的探索精神。
(二)“数学与生活”的内容分析及教材改进建议
(1)“数学与生活”的内容分析。本单元以“数学与生活”为载体渗透数学文化的内容非常多,较好地体现了数学作为基础学科的地位与价值。根据学生与现实生活的接近程度,将数学与现实生活分为两类:个人的、公共的。
“数学与生活”的内容总共出现29项,其中C1中的3项都是公共生活,C2中有11项属于个人生活,其余15项属于公共生活,个人生活与公共生活的数量差异不大,说明青岛版教材非常注重两类生活的均衡性。
进一步分析发现,“数学与生活”中的个人生活条目主要以家庭生活为主,比如“测量圆桌的周长、面积”等家庭用品为背景,较少涉及与学生个人相关的学校生活、日常生活、娱乐生活等;公共生活条目中主要以社会生活中出现的公共服务和设施为背景,比如“测量圆形花坛的周长和面积、种树、磨面的石碾”等,但对于职业生活、经济生活则较少涉及。
(2)“数学与生活”的改进建议。第一,素材内容应选择贴近学生生活的真实情境。脱离生活实际的数学往往带给学生一种抽象晦涩、深奥玄妙的灰色形象。因此,在素材选择上尽量选择情境真实、贴近学生生活,同时具有深厚文化底蕴的素材。这样既能增加学生的兴趣,又可以让学生体会数学知识在解决问题中的价值和作用。第二,素材内容选择应尽量多样化。建议尽可能涵盖数学与生活的各个领域,使日常的、学校的、社会的、经济的、娱乐的、职业的等文化类型丰富多彩,开阔学生的视野,感受数学在生活中的作用,进而体会数学应用的广泛性。
(三)“数学与科技”的内容分析及教材改进建议
(1)“数学与科技”的内容分析。根据科学技术研究的对象类型,将其分为四类:生物科学、地球科学、物质科学、高新技术。本单元中数学与科技的内容共计3项,比如介绍日本的富士山、石子落入水中产生的圆形水波、荷叶的受光面积等相关知识。说明教材非常注重数学与科学的联系,这与数学学科的本质特性有关,同时教材选择的是水波纹、荷叶等小学生生活中常见的现象和事物,符合小学生的心理特征。
(2)“数学与科技”的改进建议。数学是一门基础学科,推动着科技的发展,为科技进步带来很多意想不到的成果。现代科学技术日新月异,特别是计算机科学、人工智能领域发展迅猛,伴随着大数据时代的到来,数学的价值日益凸显,同时,数学的研究领域、应用领域也得到极大的拓展。在编写教材时,应加强数学与其他学科的联系,将不同学科的内容进行有机整合,有利于提升学生的综合素养。比如,在练习中可以增加圆形的向日葵花盘、枫树的种子以旋转的方式在地面上传播、台风以滚动的方式在海面或陆地上移动、激流以漩涡的方式汹涌向前等素材,让学生在学习数学知识和解决问题的过程中,了解其他学科的知识;再比如在学完“圆的认识”后,在练习中可以增加利用信息技术手段设计用圆组成的美丽图案,不仅有助于提升学生的兴趣、培养学生的创造能力,还有助于提升学生的美学素养。另外,“圆”属于空间与图形领域,教材中受纸质材料的限制,很多内容的呈现不够形象直观,可以利用PowerPoint、flash、3D打印等信息技术手段帮助学生加强对于圆的特征,周长、面积公式推导等知识的理解,从而培养学生的空间观念与空间想象能力,体会模型思想。
(四)“数学与人文艺术”的内容分析及教材修订建议
(1)“数学与人文艺术”的内容分析。根据艺术形式的不同,分为四类:人文、美术、音乐和建筑。“数学与人文艺术”的内容在C1和C2中均有出现,共计8项。
本单元涉及中国古代建筑天坛、英国的巨石阵等,这说明教材关注到了数学与人文艺术的联系,但从整体看来,数学与人文、数学与音乐、数学与建筑的类型还不够丰富。
(2)“数学与人文艺术”的改进建议。本单元“数学与人文艺术”的内容中,没有涉及与音乐相联系的内容,说明教材对数学与音乐这方面的关注度不够,建议增加与音乐有关的内容,如以阅读材料的形式呈现“圆周率之歌”,把小学生喜爱的音乐与数学有机地融合起来,让学生了解数学符号与音乐的关系,感受数学美的熏陶;数学与建筑方面虽有涉及但内容不多,古今中外都有大量的与圆有关的著名建筑,教材可以增加更多的与建筑相关的素材;最后,适量增加数学与美术方面的背景素材。美术素描中基础图形圆的绘画方法就是典型的圆出自方的诠释和割圆术的反证。
二、数学文化在教材中的运用水平
就教材中数学文化的运用水平而言,采用王建磐等提出的框架进行分析,将数学教材中数学史的运用水平分为点缀式、附加式、复制式、顺应式四类。将其余类型的数学文化运用水平分为外在型、可分离型和不可分离型三类。
(一)数学史的运用水平
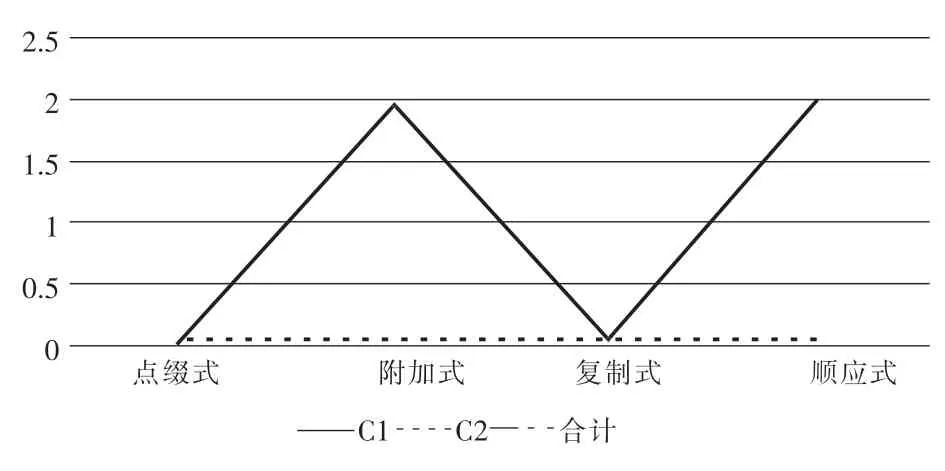
表2 《圆》一章中数学史的运用水平
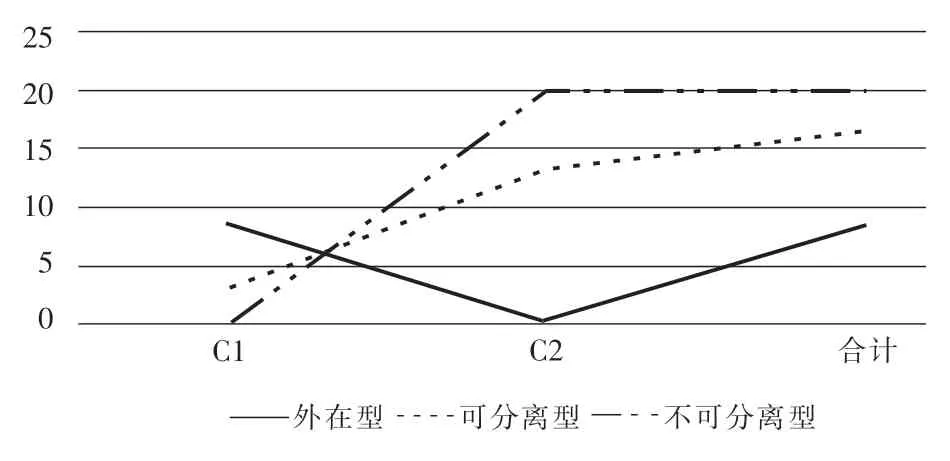
表3 《圆》一章中其他数学文化类型的运用水平
教材中祖冲之的介绍属于附加式,圆周率以及圆的面积推导属于顺应式。可见,青岛版教材对于数学史的运用水平较高。以往的教材中,更多的是把数学史放到“你知道吗?”中,青岛版教材将数学史与教学内容有机融合,充分体现了数学文化的教育价值,其史料内容的介绍与学生的认知结构相统一。比如在“圆的面积”推导中,将有关的史料放入教材例题的学习中,从而将数学史与教学知识内容完美结合,避免了数学文化运用水平的浅层化。教材以几个学生交流的方式呈现了圆的外切正多边形和内接正多边形无限逼近以及用拼割法把圆转化为平行四边形或长方形的研究方法,隐含着古代中外数学家们关于“圆的面积”的探索历程。教材对史料内容的运用水平较高,学生在思考与探究中,既学到了圆的面积推理的方法,又领略了古人的智慧以及数学家孜孜不倦的求真求实精神。因此,教材编排独具匠心,彰显了数学教学的文化味,将数学的科学性与人文性有机结合。
(二)其余类型的数学文化运用水平
就其他数学文化类型的运用水平而言,外在型8项;可分离型18项;不可分离型22项。见表3。
教材中有一半多的条目属于不可分离型,可见教材关注了数学文化与数学知识的关联。可分离型的条目有16项,占比不到一半。可分离的应用情境主要出现在练习中,要解决的问题不是情境本身,情境只是附加的干扰性,只需要用数学知识解决隐藏的数学问题。比如:“求时针的尖端走过的路程是多少厘米?”显然这是强加给这个情境的,在真实生活中没有人会去计算分针走过的路程。
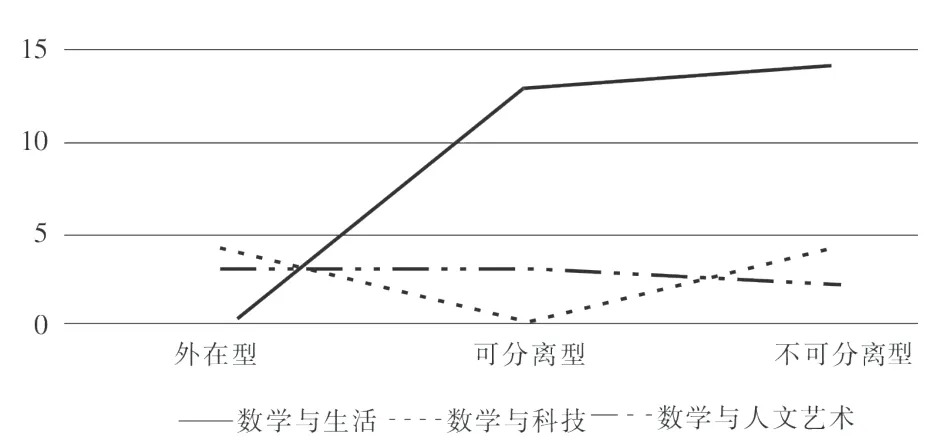
表4 《圆》一章中其他数学文化类型的运用水平
进一步分析《圆》单元中不同类型数学文化的运用水平可以发现(见表4),“数学与生活”超过50%的项目属于不可分离型的运用水平,“数学与科技”有50%属于不可分离型的运用水平,说明两种文化类型在本单元中数学文化运用水平较高,“数学与人文艺术”的运用水平分布比较均衡。
整体来看,青岛版教材中数学文化内容多采用顺应式和不可分离型的运用方式,运用水平较高。其中,可分离型占18项,占一定的比例,说明有些数学文化的内容与数学知识的关联度不高。为了进一步提高数学文化内容的运用水平,就要充分发掘与筛选更多的文化素材,以更加自然的方式融入数学中,成为数学问题的有机组成部分,让学生真正体验到“数学本质上就是一种文化”,否则会给教师和学生一种从外部强加背景或者贴标签的生硬的感觉。用数学知识解释生活现象,使问题内生于情境,情境服务于数学学习,从而实现数学与文化二者的有机融合。
三、数学文化在教材中的功能
数学文化在教材中的功能借鉴Dickenson-Jones的分类,将数学文化的功能分为提供背景性情境、提供应用性情境、拓展数学思维与方法、促进数学与文化交融、体验文化实践。
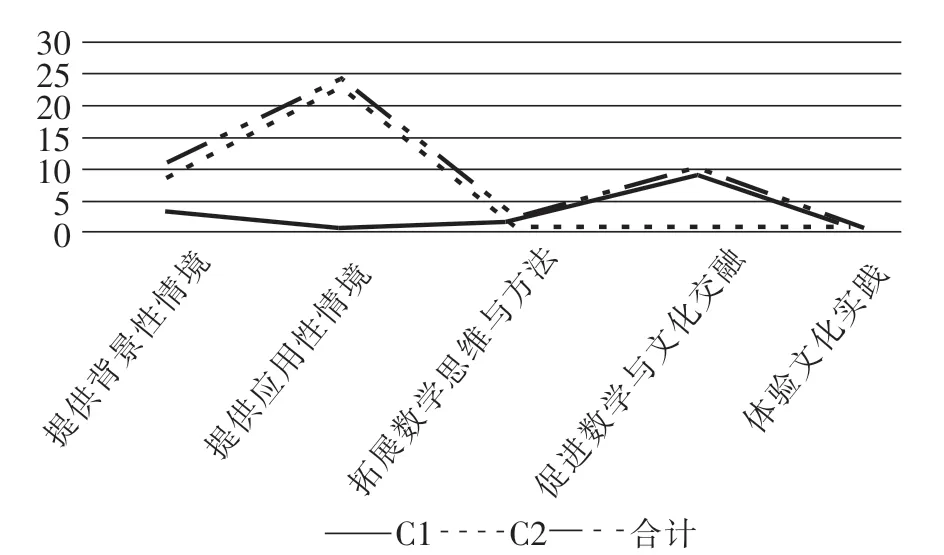
表5 《圆》一章中数学文化功能
从以上数据可以看出,数学文化功能主要体现在提供应用性情境上,大多出现在练习中。教材关注数学在各个领域中的应用,关注数学的应用价值;其他类型也有所涉及,比如数学史以促进数学与文化交融为主,这表明教材也充分考虑了数学文化价值的丰富性。青岛版教材丰富而全面地呈现了数学文化的各类功能,而且各个文化类型的功能定位也不同。
比较C1和C2中的数学文化功能可以发现,C1以提供背景性情境和促进数学与文化交融为主,C2则是以提供背景性情境和提供应用性情境为主。出现这一现象与栏目本身的特点有关,教材编排注重与圆相关的各种背景知识,并且注重用学到的圆的有关知识解决生活中的实际问题,有利于学生建立数学与生活的关系,体会数学的作用。
进一步分析各种数学文化类型的功能可以看出(见表6),数学史的功能主要是“拓展数学思维与方法”和“促进数学与文化交融”;数学与生活的功能主要是“提供应用性情境”,其次是“提供背景性情境”;数学与科技的功能主要是“促进数学与文化交融”和“提供背景性情境”;数学与人文艺术的功能以“促进数学与文化交融”为主。总体而言,青岛版教材中各种数学文化类型的功能比较丰富。
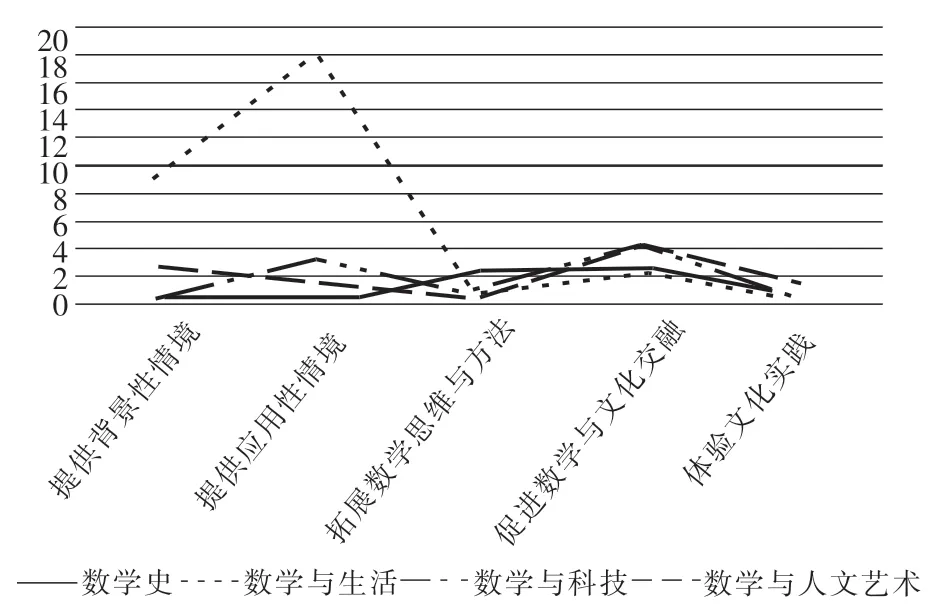
表6 《圆》一章中不同类型数学文化的功能
本文从数学文化类型、数学文化运用水平、数学文化的功能三个维度,以《最美的图形——圆》单元为例,分析了青岛版数学教材中数学文化的渗透情况,为教师提供了从数学文化视角研究教材的可操作的方法,有助于教师找准教材中数学文化的渗透点,全面领略数学文化功能,充分发挥数学课程的育人功能。
