面向高通量计算机的图算法优化技术
2020-06-23张承龙曹华伟王国波郝沁汾叶笑春范东睿
张承龙 曹华伟 王国波 郝沁汾 张 洋 叶笑春 范东睿
1(计算机体系结构国家重点实验室(中国科学院计算技术研究所) 北京 100190)2(中国科学院大学计算机与控制学院 北京 100049)
图具有极强的抽象性和灵活性,是一种表示和分析大数据的有效方法.图计算可进行巨量、稀疏、超维关联的挖掘和分析,已广泛应用于社交网络、交通网络、生物信息网络、知识图谱等[1-4].随着图数据规模的爆炸式增长和图计算需求的不断增加,如何高效地处理大规模图数据成为大数据领域的研究重点,也是工业界关注的焦点.
宽度优先搜索(breadth first search, BFS)算法是一种经典的图遍历算法,也是众多图分析算法的基础,例如连通分量(connected component, CC)、中介核心性(betweenness centrality, BC)以及单源最短路径(single-source shortest path, SSSP)等算法.BFS应用具有数据局部性差、计算访存比低、并行效率低和扩展性差等数据密集型应用的典型特征.2010年,国际上提出了Graph500排行榜来评估服务器和超级计算机处理数据密集型应用的能力,而BFS算法是Graph500的基准测试程序之一[5].
针对数据密集型应用,中国科学院计算技术研究所高通量计算机研究中心在2018年的中国计算机大会上发布了新一代高通量计算机“金刚”[6].高通量计算机(high-throughput computer, HTC)采用高通量众核体系结构,在一系列体系结构创新技术的加持下,高通量计算机具有高并发、强实时、低功耗等适于大数据计算的特点.目前,高通量计算机已经针对深度学习、高通量视频处理、科学大数据处理和信息安全监测等典型场景开展示范引用.
本文将对单节点下BFS算法的优化技术进行系统介绍,并在此基础上提出2种面向高通量计算机的优化手段,通过减少冗余访存和提高缓存局部性,有效提高了算法的访存效率.基于这些优化手段,我们对BFS算法在高通量计算机上的性能进行系统的评估,同时与通用服务器进行对比,展现高通量计算机处理数据密集型应用的优越性.
1 相关工作
为了获取更高的性能和更低的能耗,近年来BFS的并行算法在共享式内存系统、分布式内存系统和GPU等平台上都得到了广泛的研究,国际上针对BFS算法的优化工作也取得了一系列的进展.
在Cray的MTA平台上,Bader等人[4]通过挖掘算法的并行度,采用多线程技术来隐藏遍历过程中的访存延迟.Agarwal等人[7]针对数据结构进行优化,改善了数据的局部性,提高了算法性能.为了充分利用GPU的多线程技术,Hong等人[8]提出一种面向GPU平台的并行BFS算法,结合多线程技术和细粒度同步机制提高了系统的整体性能.2011年,Beamer开创性地提出了一种自底向上(bottom-up)的遍历算法[9],通过结合传统自顶向下(top-down)的算法,实现了方向性优化的BFS算法,通过减小冗余的访存开销,提高了算法性能.2015年,叶楠等人在在众核体系结构上对BFS算法进行了测试,发现当前典型的众核结构无法满足BFS算法的需求,新型处理器体系结构需要支撑大量离散随机访问以及更为简单的执行机制[10].2013年,Yasui等人针对非统一内存访问架构(non-uniform memory access architecture, NUMA)提出了相应的NUMA感知和度数感知优化技术,在Intel的四路Xeon E5-4640服务器上取得了29.1 GTEPS的性能[11].基于上述研究,我们发现BFS并行处理时仍然存在严重的负载不均衡性,基于此提出一种静态shuffle优化,改善了众核间的负载均衡性,显著提高了线程利用率,同时也避免了动态调度方式的一些缺点[12].
本文在已有工作的基础上,提出了一种高效的基于块查找的位图访问方式,减少了不必要的缓存访存;此外,我们对Bottom-up算法的遍历过程做了进一步优化,有效改善了缓存数据的局部性,提高了访存效率.
本文主要贡献有3个方面:
1) 为了充分利用高通量计算机的大容量缓存,提出一种高效地位图访问方法,显著提高了未访问点的查找效率,能够显著减少对cache的访问,提高寄存器访问的局部性.
2) 针对Bottom-up的核心算法进行了深入优化,将3个bitmap减少为2个bitmap,在此基础上将Degree-Aware中的2次遍历过程合并为一次,提高了缓存局部性和分支效率.
3) 在高通量计算机上对BFS的性能和能耗表现进行了系统评估,并与x86架构的服务器进行了对比.详细分析了所提算法的有效性,优化后的算法显示出性能和性能功耗比优势.
2 算法背景介绍
本节我们将对BFS算法及现有的优化技术进行系统的介绍和总结,包括方向性优化、去零点优化、度数感知优化、顶点排序优化和静态shuffle优化等.最后的实验也是集合了这些优化技术.
2.1 方向性优化
传统的BFS算法是一种自顶向下(top-down)的遍历方法,遍历中后期会产生大量的冗余遍历.Beamer创造性地提出了一种Bottom-up 算法来减少冗余边的遍历.如算法1所示.
算法1.Bottom-up BFS算法.
输入:图G={V,E}、遍历起始点s;
输出:存储父亲信息的数组parent.
①visit[v]←0, for ∀v∈V;
②visit[s]←1;
③parent[s]←s;
④currentfrontier←{s};
⑤nextfrontier←∅
⑥ whilecurrentfrontiernot empty do
⑦ for eachu∈Vin parallel do
⑧ ifvisit[u]==0 then
⑨ for eachwadjacent toudo
⑩ ifw∈currentfrontier
{u};
Bottom-up采用与Top-down完全相反的思想,在算法1执行的每一层优先选择所有未访问的顶点(行⑧),通过查找其邻居顶点是否位于currentfrontier来替子节点寻找父节点.一旦未访问的顶点在currentfrontier中找到父节点,则跳出循环结束对剩余邻居顶点的访问,有效减少了冗余的访存开销.由此导致Bottom-up算法在初始几层遍历时产生大量的无效遍历.基于此,Beamer等人提出结合Top-down和Bottom-up的方向性优化算法[9].在算法1中,首先使用Top-down算法开始遍历,当currentfrontier队列变得足够大时切换到Bottom-up执行,结合二者的优势,从而显著提高BFS性能.
2.2 去零点优化
在Graph500中,数据集采用的是Kronecker生成图.研究发现[11],Kronecker生成图中存在大量的孤立顶点,即这部分顶点的出度为0.通过统计,孤立顶点在不同规模的生成图中所占比例如表1所示:

Table 1 Ratio of Isolated Vertices in Kronecker Graphs with Different Scales表1 不同规模下的Kronecker生成图中孤立顶点的比例
从表1可以看出,孤立顶点在Kronecker生成图中的占比超过50%,并且随顶点规模的增加而增长.Bottom-up算法在遍历每一层的过程中,首先会从所有顶点中找出所有未被访问过的顶点,然后从这些未访问过的顶点出发去搜索其父亲节点.孤立顶点的存在,使得Bottom-up算法在每层遍历中,产生大量对孤立顶点的无效遍历和无效访存.因此,在预处理中去掉孤立顶点,会进一步提高遍历效率.
2.3 度数感知优化
如2.1节所述,Bottom-up算法遍历中会扫描所有未访问顶点的邻居顶点,只要找到一个邻居顶点在currentfrontier中,则结束对剩余邻居节点的遍历.如果终止的越早,则可以减少邻居检查的数量.理想情况下,Bottom-up方法只检查未访问顶点的第1个相邻节点,就能够检查成功,其后将跳过所有剩余的邻居顶点.然而事实上,我们难以确定邻居列表的最佳顺序,选定不同的源顶点,邻居列表的最佳顺序都可能是不同的.Yasui等人通过实验发现了顶点度数和访问频率之间的关联性,顶点的度数越大,其访问频率越高[13].为了进一步提高访存效率,Yasui将邻接列表A拆分为只含最高度数邻居顶点的AB+与剩余按照度数降序排列的邻接列表AB-,将算法1中的一次遍历循环(行⑨~)拆分为采用邻接列表AB+与AB-的2次循环.实验发现,度数感知优化可以极大减少冗余边的遍历,提高数据访问效率.
2.4 顶点排序优化
为了改善数据的局部性、提高访存效率,Yasui等人提出一种顶点排序的优化方法[14],基于顶点度数降序对行列表(row)中的顶点索引进行排序,将较低的索引分配给具有高度数的顶点.尽管顶点排序方法可以改进数据的局部性来减少访存开销,但是在动态调度过程中,数据块粒度和调度开销存在博弈.当块粒度很小时,可以很好地解决线程间的负载均衡问题,但频繁的线程调度将显著提高执行时间的开销,导致整体性能下降.当块粒度很大时,由于图数据顶点度数分布遵循幂律分布[15],因此相邻顶点块中度数分布变化很大.高度数块的处理时间远大于低度数块的执行时间,导致严重的负载不均衡问题.
图1显示了顶点排序方法下线程的平利用率,可以看到采用动态调度的方式每个线程的利用率波动很大,线程间存在严重的负载极不均衡问题.
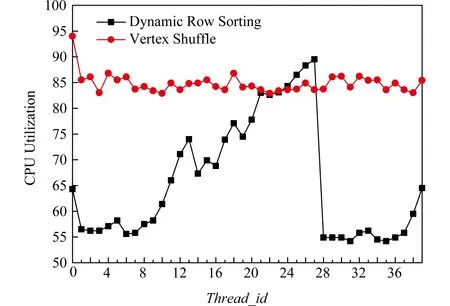
Fig.1 The thread utilization of two methods when 2scale=227图1 当规模为227时2种方法的线程利用率
2.5 静态shuffle优化
针对高通量计算机高并发的体系结构特点,我们在之前的工作中提出了一种按照顶点度数轮询分配的静态shuffle优化方法[12],在利用顶点排序优势的同时,改善了高通量计算机核间的负载均衡性,提高了并行BFS算法在高通量计算机上的性能.
如算法2所示,在图数据的CSR存储结构中,对行列表row中的顶点按度数降序排序,以轮询的方式依次将顶点分配给不同段数组(分别存储线程执行顶点信息),保证高度数顶点与低度数顶点均匀地分配给每个线程,并在线程段数组内依然保持顶点按度数的降序排列.与此同时,建立新顶点ID到旧顶点ID的映射,从而可以在图遍历结束后恢复原始图拓扑的父节点信息.
算法2.顶点轮询分配的静态shuffle算法.
输入:划分个数segmentNum、原始的排好序的row缓存old_array;
输出:shuffle之后的row缓存new_array、节点shuffle前的编号new2old.
①num←vertexNums/segmentNums;
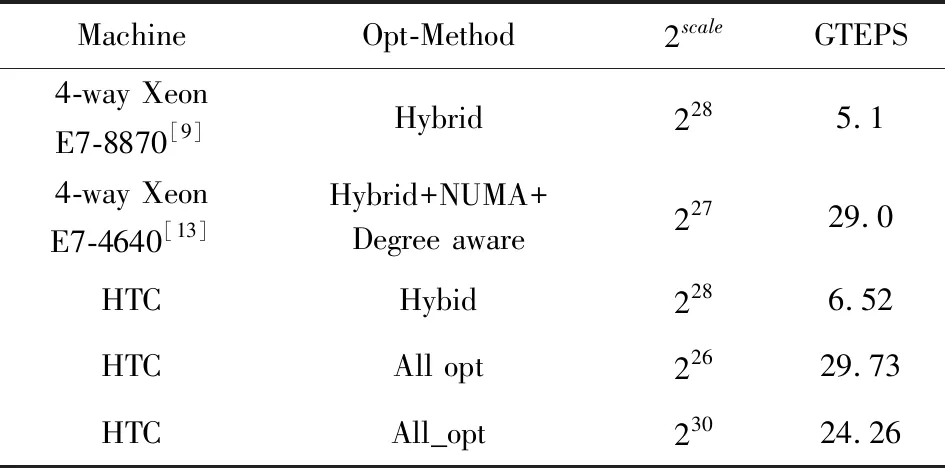
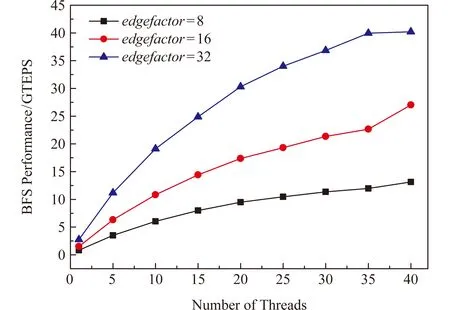
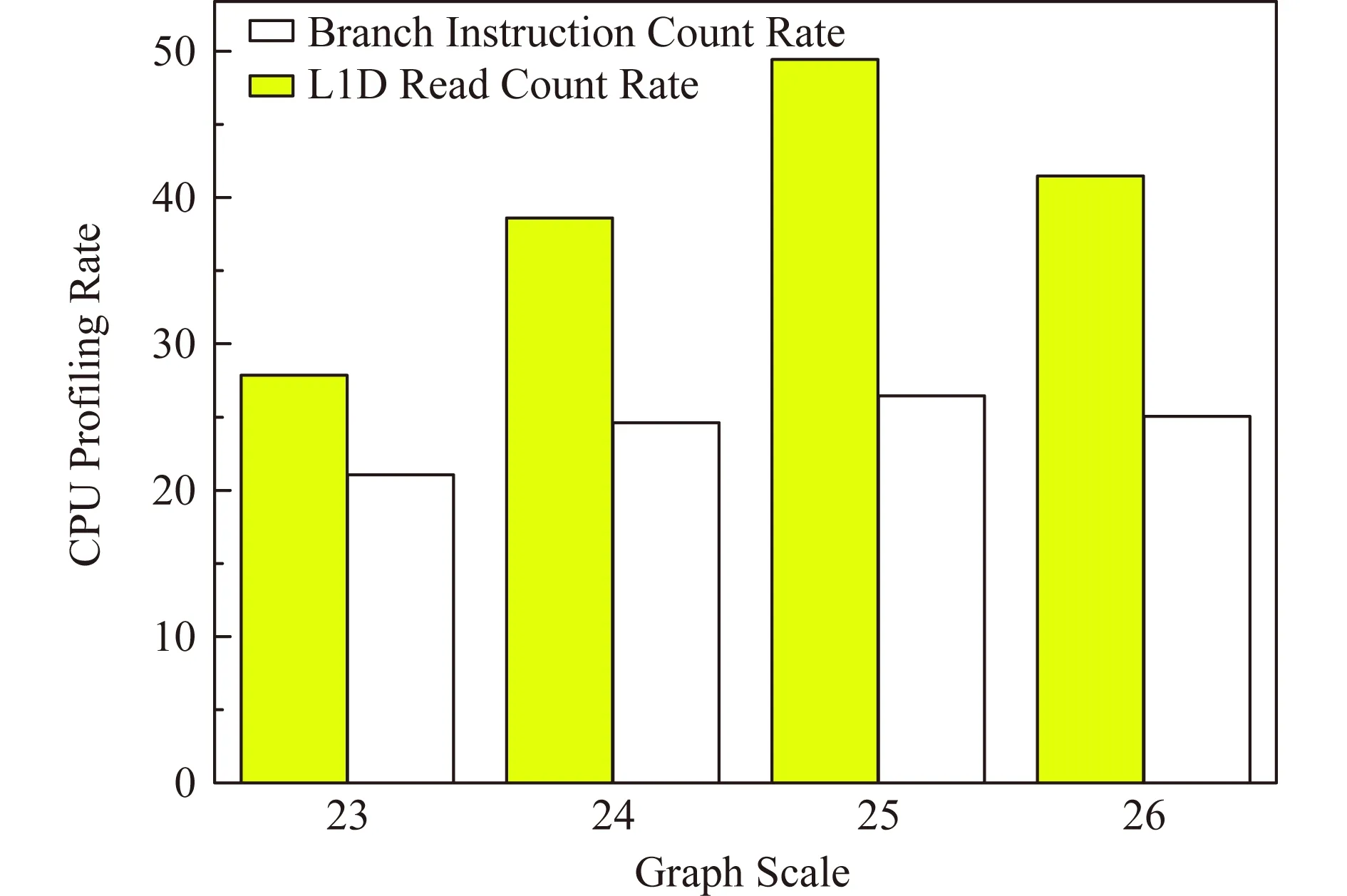
② for(tid=0;tid do ③ for (j=0;j ④new_array[tid×num+j]← old_array[tid+segmentNums×j]; ⑤new2old[tid×num+j]←tid+ segmentNums×j; ⑥ end for ⑦ end for ⑧ returnnew_array,new2old. 通过上述静态shuffle分配,一方面保持了顶点排序的数据局部性,提高了内存带宽的利用率;另一方面,在预处理时已经将每个线程处理的顶点信息保存下来,避免了频繁的线程调度引起的开销,以及动态分配中块粒度的经验参数调整. 针对高通量计算机高并发和大容量缓存的体系结构特点,我们在第2节优化工作的基础上,提出了基于块查找的位图访问优化和Bottom-up遍历优化2种方法,进一步提高BFS算法在高通量计算机上的性能.具体来说,我们提高了未访问顶点的搜索效率与片上缓存的数据局部性,有效提高了BFS算法的访存效率. BFS在遍历过程中采用位图的形式来标记顶点的访问状态.位图是一种紧凑的数据结构,可以放在最后一级缓存(cache)中,有效减少了片外DRAM的访问,降低了访存开销.在Bottom-up算法中,每次迭代都通过顺序扫描visit位图来寻找未访问顶点(算法1行⑦~⑧).由于Kronecker图结构的幂律分布特点,经过几次Bottom-up迭代后,未访问顶点的数量将急剧减少,并呈稀疏分布.在处理大规模图数据时,顺序扫描visit位图将对性能产生极大的影响. Fig.2 The quick search for unvisited vertices图2 未访问顶点的快速遍历示意图 基于此,我们提出一种基于块(block)查找的visit位图访问优化技术,在每一层的Bottom-up遍历中,能快速找到未访问顶点在block中的位置.如图2所示,在遍历过程中以visit位图中的block为单位进行顶点状态的粗粒度判断.现代通用处理器中通用寄存器的最大位宽为64位,最多可以表示64个点的访问状态,因此一个block的大小设置为64.在遍历开始时,首先将visit位图中第i个block的访问状态从内存中加载到64位宽的寄存器block_visit中.然后,对visit位图的第i个block对应的整型变量block_visit取反,得到寄存器变量block_no_visit,取反后状态位为0是已遍历的顶点,状态位为1则为待查询的未访问顶点.如果block_no_visit中的状态位全为0,则说明当前block不包含未访问顶点,直接跳过对当前block中所有顶点的状态访问;如果block_no_visit的状态位不全为0,通过算法3可以快速定位block_no_visit中最右侧的未访问顶点的位置(最右侧1 bit位),并将寄存器block_no_visit中该点对应的位置置0,依次循环,从右到左依次访问block_no_visit中的未访问顶点(bit位为1),如图2所示.在从block_no_visit中查找未访问点时,其循环次数仅与bit位为1的数目(即未访问的顶点数目)有关,而与block大小无关.而传统算法在查找block中未访问点时采用顺序遍历,即使block中只有1个未访问点,也需要迭代block大小次数. 算法3.基于块查找的顶点快速定位. 输入:一个block 的遍历状态(uint64_t)block_no_visit(block_no_visit=1表示尚未遍历,block_no_visit=0表示已经遍历); 输出:一个block寄存器变量中最低位未遍历点的位置pos、 更新之后的block_no_visit. ① uint64_tbit_no_visit=block_no_visit& (-block_no_visit); ② uint64_tmask=bit_no_visit-1; ③pos=__builtin_popcountl(mask); ④block_no_visit=block_no_visit& ~bit_no_visit; /*set the lowest unvisited vertex to visited*/ ⑤ returnpos,block_no_visit. 算法3中核心函数的算法复杂度为O(log(k)),优于传统顺序查找的算法复杂度O(k).优化后,将原有的细粒度逐位扫描方式,转换为粗粒度的快速定位方式,在Bottom-up的后几层遍历过程中,减少了大量的访存操作.此外,BFS算法的局部性非常差、cache miss率高,会发生频繁的cache替换.本节提出的基于块查找的位图访问方法,将一个block的位从原有的visit位图存入寄存器,减少了对cache的频繁访问,提高了访问效率.引入块查找位图访问后的Bottom-up遍历如算法4所示. 算法4.使用3个bitmap的块查找的Bottom-up算法. 输入:图G={V,E}={V,(AB+,AB-)}、遍历起始点s; 输出:存储父亲信息的数组parent. ①visit[v]←0, for ∀v∈V; ②visit[s]←1; ③parent[s]←s; ④currentfrontier←{s}; ⑤nextfrontier←∅ ⑥BlockNum←vertex_num/BlockSize; /*顶点总数vertex_num除以block宽度BlockSize*/ ⑦ whilecurrentfrontiernot empty do ⑧ fori0~BlockNumin parallel do /*当前层遍历,依次取每个block*/ ⑨block_visitgetBlock(visit,i); /*获取第i个block的访问状态,存入寄存器变量block_visit*/ ⑩block_no_visit~block_visit; (block_no_visit); /*block中最右侧未访问点的位置pos*/ then /*如果v在当前层*/ (1≪pos); (1≪pos); 表2给出了优化前后Bottom-up每层遍历的顶点数目对比.可以看出,在遍历到第5层时,99.8%的顶点是已访问状态,顺序扫描visit位图将产生大量无效访存.优化后,每次以粗粒度的block进行判断,对于包含未被访问的顶点,基于块查找的位图访问优化可以高效地定位未访问顶点.相对于顺序扫描,最多能节省98.4%的顶点访存状态判断,极大地提升了算法的遍历效率. Table 2 Number of Traversed Vertices with and without Bitmap Optimization表2 位图访问优化前后的顶点遍历数目 在本节中,我们提出针对Bottom-up遍历方式的优化.在原有的Bottom-up算法中,需要current_frontier,next_frontier和visit三个数据结构来保存遍历过程中更新的信息.current_frontier保存当前层的活跃顶点,visit保存已经被遍历过的顶点,next_frontier用于存放下一层将遍历的活跃顶点.事实上,visit中包含处于current_frontier中的活跃顶点信息,位于current_frontier中的顶点一定已经在visit中置位,因此在判断未访问顶点u是否有邻居顶点在current_frontier中时,我们考虑用visit位图代替来达到同样的效果,减少额外数据结构的使用.如算法5的行~所示,结合使用visit和visit_new,能够在遍历过程中省去对当前层的跃顶点结构current_frontier的访问,将Bottom-up遍历过程中所需要的3个数据结构减少为2个,每次迭代只有一次visit读操作和一次visit_new写操作,其余操作都是对寄存器block_visit进行的,提高了cache访问的缓存局部性,进而提高了访存效率. 算法5.基于块查找的Bottom-up BFS算法(block search bottom-up BFS, BSBB). 输入:图G={V,E}={V,(AB+,AB-)}、遍历起始点s; 输出:存储父亲信息的数组parent. ①visit[v]←0, for ∀v∈V; ②visit[s]←1; ③parent[s]←s; ④currentfrontier←{s}; ⑤nextfrontier←∅; ⑥BlockNumvertex_num/BlockSize; /*顶点总数vertex_num除以block宽度BlockSize*/ ⑦ whilecurrentfrontiernot empty do ⑧ fori0~BlockNumin parallel do /*当前层遍历,依次取每个block*/ ⑨block_visitgetBlock(visit,i); /*获取第i个block的访问状态,存入寄存器变量block_visit*/ ⑩block_no_visit~block_visit; (block_no_visit); /*block中最右侧未访问点的位置pos*/ /*如果v在当前层*/ (1≪pos); 另一方面,在Yasui等人提出的度数感知优化中[14],阐明了Bottom-up算法的主要性能瓶颈是对未访问顶点的邻居顶点的访存开销.他们将邻接列表A拆分为只含最高度数邻居顶点的AB+与剩余按照度数降序排列的邻接列表AB-,分别遍历2个邻接列表来提高邻居顶点在current_frontier中的搜索效率.我们进一步统计了Bottom-up算法在邻接列表AB+与AB-的遍历效率,测试结果如算法5所示. 表3可以看到,在Bottom-up算法的每层遍历中,通过邻接列表AB+更新的活跃顶点数目超过96%,并且随遍历层数的推进,活跃顶点的比重不断增加.在测试样例的第5层遍历中,所有的活跃顶点都是通过邻接列表AB+更新.基于此,在我们优化后的Bottom-up算法中,我们将对邻接列表AB+与AB-的遍历合并为一个,在保证AB+数据局部性的同时,又减少了对AB-结构无效的访存次数. Table 3 Number of Active Vertices Under Degree-aware Optimization for Graph Scale 227表3 顶点规模为227时度数感知优化下Bottom-up 每一层遍历的顶点数目 为了评估高通量计算机处理大规模图数据的能力,我们搭建了2套测试系统用于评估BFS算法的性能.一套基于自研的高通量计算机,配备一颗ARM架构的Centriq 2434众核处理器,该处理器包含40个处理核心和50 MB的L3 cache,TDP为110 W;另一套系统采用传统的x86架构服务器,配有两路Intel Xeon E5-2683处理器,每路CPU包含14个核心和35 MB L3 cache,TDP为120 W.系统的详细配置信息如表4所示,2套系统均使用gcc7.3.0进行编译. Table 4 Configure Information表4 系统配置信息 测试数据集采用Graph500基准测试中的Kronecker生成图,其参数设置为默认值(A=0.57,B=C=0.19,D=0.05).Kronecker生成图可以通过输入scale和edgefactor等参数来调整图的性质,其中,scale参数表示图的顶点规模,edgefactor表示每个顶点的平均度数.生成的图数据满足幂律分布,包含2scale的顶点数目以及2scale×edgefactor的总边数.对于每个测试数据图,随机选择64个源顶点执行BFS算法并取平均时间,采用指标每秒遍历亿条边 (giga-traversed edges per second, GTEPS)来对性能进行评估. 实验用的高通量计算机主要用于数据中心大数据处理[16],其微结构主要包括:1)高吞吐处理核.共有40个处理核,每个处理核采用变长流水线和多发射结构,显著提高了指令吞吐效率,有效地掩盖了图遍历过程中邻居边访问时延.2)大容量片上存储.高通量计算机具有较大容量的L3 cache,大小为50 MB,可以将更大的图放到缓存中,进一步提高了访存局部性.3)易扩展片上网络.处理核通过环形总线进行互联,可以提供250 GB/s的聚集带宽,能够满足图遍历时的核间数据共享带宽需求.4)快速同步机制.支持基于数据流的核间细粒度快速同步,相比传统的基于内存的同步机制,性能可获得数量级的提升,有效缓解了每次迭代后的层同步压力.5)可编程数据通信机制.可编程数据传输引擎结构,可以快速实现数据的水平 (片上处理器核之间)和垂直(从内存到片上存储)搬运,实现了数据通信的低延迟.高通量计算机有效解决了高通量典型应用BFS的缓存利用率低、内存访问效率低等问题. Fig.3 BFS performance on HTC with different graphscale and edgefactor=16图3 不同规模的图数据在平均度数为16的高通量计算机上的BFS性能 图3给出了顶点规模为224~230,平均度为16的Kronecker生成图在高通量计算机上执行BFS算法的性能变化趋势.在不做任何优化时,Graph500基准程序的平均性能只有0.69 GTEPS,生成图顶点规模对性能的影响较小.采用方向性优化后(Hybrid),性能得到明显提升,平均性能达到了6.52 GTEPS,性能提升趋势与Beamer采用四路Xeon E7-8870的结果(5.12 GTEPS)[9]基本一致.基于Yasui提出的去零点优化(remove zero, RZ)和度数感知优化(degree aware, DA)[13],我们提出了静态shuffle优化[12]来改善线程间的负载均衡性.如图3所示,优化前的最优性能为25.92 GTEPS,在顶点规模为226时取得.随着图顶点规模的增加,性能呈下降趋势.增加本文提出的位图访问优化和Bottom-up遍历优化之后,由于访存效率的改善,对于226的图,BFS算法在高通量计算机上提升到了29.71 GTEPS,且性能随图顶点规模的变化趋势与之前基本一致.相比Graph500的基准测试程序,实现了43.01倍的性能提升.对于所有SCALE的性能,性能平均提高11.4%.充分说明了本文提出方法的有效性.表5对近年来基于CPU和高通量计算机的BFS优化工作进行了汇总.通过对比,进一步说明高通量计算机在图处理领域具有显著的优越性. Table 5 Compare with Related Work表5 与相关工作对比 Fig.4 Scalability of BFS Algorithm on HTC图4 BFS算法在高通量计算机上的扩展性 为了研究优化后的BFS算法在高通量计算机上的扩展性,针对顶点规模为225的图数据,图4和表6给出了不同线程数目下的BFS性能变化.在平均度为16时,40线程下的高并发处理比单线程的性能提升了将近17.8倍,同时性能随线程数目的增加呈近似的线性扩展.随后我们对平均度数的影响进行了研究.由图4可以看出,随着平均度数的增加,算法性能提升幅度明显,平均度数越高,性能越好.在平均度为32时,算法的平均性能可以达到40.2 GTEPS,优于平均度为16时的27.2 GTEPS和平均度为8时的13.14 GTPES.这主要是由Kronecker生成图的特性造成的.随着平均度的增加,Kronecker生成图将会产生大量的重复边,降低了图数据的稀疏性.这些重复边在BFS的遍历过程中不会对运行时间造成影响,进而表现出更优的搜索效率.为了保证图拓扑结构的稀疏性,我们在后续的实验中选用Graph500中默认的16作为生成图的平均度. Table 6 Scalability and Speed-up Under Different Numbers of Threads表6 不同线程数目下的扩展性和加速比 Fig.5 CPU profiling parameters with and withoutthe optimizations图5 优化前后的CPU参数对比 本文提出的块查找位图访问优化、Bottom-up遍历优化主要是对L1 Data Cache访存和分支跳转进行的优化,因此本节使用Perf对优化前后的Bottom-up函数进行了代码插装,获取了L1 Data Cache(L1D)读访问次数、Branch指令数的变化情况,进一步验证我们算法的有效性.如图5所示,L1D读访问次数平均减少了24.29倍,因为块查找位图访问优化对L1 Data Cache按照block的粒度进行读取,将顶点数据读取到寄存器中,即使block中所有点都需要判断,也只需读取一次cache,后续操作都是针对寄存器的运算.Branch指令数平均减少了39.34倍,这是因为块查找位图算法复杂度低,能够快速找到未判断的点,减少了分支指令次数.上述性能分析说明本文的优化手段有效改善了缓存局部性和分支效率,提高了访存效率. 本节将对比分析BFS算法在高通量计算机和x86服务器上的性能,图6给出了优化后的BFS算法在高通量计算机和通用x86服务器下执行的性能对比,默认采用的优化手段为方向性优化、去零点优化、度数感知优化、静态shuffle优化以及本文提出的优化方法.如表4所示,我们使用的x86服务器拥有2个NUMA节点,当CPU访问非本地NUMA上的数据时,产生较长的访存时延.在文献[11]中,作者提出针对多NUMA架构的性能优化方法,保证线程在执行BFS遍历时只访问本地的DRAM,避免了远程DRAM的访问开销.因此,在x86服务器上,我们增加了NUMA感知优化手段.由图6可以看出,BFS算法在两路x86服务器上的整体性能与高通量计算机大致相仿,在顶点规模为226时,x86服务器上的最优性能为23.94 GTEPS.在绝对性能方面,高通量计算机展现了优越的表现.表7给出了不同图规模下高通量计算机相比x86服务器的性能加速比.可以看出,在大规模的图数据集下,高通量计算机的执行性能全面占优.在顶点规模为227时,最大性能加速比有1.31倍. Fig.6 Performance comparison of BFS between HTCand x86 Server图6 BFS算法在高通量计算机与x86服务器的性能对比 Table 7 Performance Comparison Between HTC and x86 Server 2scaleSpeed-up2241.072251.172261.242271.312281.182291.082301.18 然而,多NUMA感知的优化方法增加了额外的编程复杂度,需要针对Top-down和Bottom-up过程分别进行不同的数据预处理,而且为避免线程跨NUMA节点访问远程数据,需要在每个NUMA节点的本地内存增加额外的数据结构,满足Top-down和Bottom-up的遍历需求,这同时也会引起内存膨胀.如图7所示,在使用NUMA优化后,内存的占用率提升了将近1.3倍.在图的顶点规模为230时,高通量计算机系统的内存使用接近350 GB,而采用NUMA感知优化的x86服务器内存占用超过420 GB.对于共享式内存系统,内存占用率是影响图数据处理规模的核心因素.综上,高通量计算机本身虽然无需采用NUMA优化,但是加入本文优化方法后在性能上可以超过额外增加NUMA优化的x86服务器,说明本文提出的方法能够发挥高通量计算机的性能,而且与传统计算机相比,高通量计算机占用的内存更少、编程复杂度也更小,高通量计算机在图数据处理方面具有显著的优势. Fig.7 Memory Consumption with and withoutNUMA optimization图7 NUMA优化前后的内存使用 本节将围绕能效方面展开研究.测试数据采用顶点规模为230、平均度为16的Kronecker大图数据,并采用微型电力监测仪实时监测2套系统的功耗.实验结果如表8所示,未经优化的Graph500基准测试程序的性能功耗比仅为2.41 MTEPS/W.采用之前的优化方法优化后性能功耗比为165.97 MTEPS/W,增加本文提出的优化方法BSBB后,高通量计算机的整机功耗为134 W,性能功耗比为181.04 MTEPS/W,性能功耗比显著提高.x86服务器的整机功耗为286 W,性能功耗比为71.92 MTEPS/W.面向超大规模的图数据集,高通量计算机相比x86服务器在单节点上拥有2.51倍的性能功耗比优势.高通量计算机的性能功耗比结果在2019年6月发布的Green Graph500面向大数据集的排行榜上可以排名第2位[17].综上,高通量计算机的高并发和低功耗等特点非常适合处理大规模图计算等数据密集型应用. Table 8 Energy Efficiency of BFS Implementation Between HTC and x86 Server表8 高通量计算机与x86服务器的性能功耗对比 (2scale=230) 本文对单节点的并行BFS算法和BFS算法的优化技术进行了介绍,并在此基础上提出2种面向高通量计算机的优化手段块查找位图优化和Bottom-up遍历优化,提高BFS的缓存局部性和访存效率.基于上述的优化手段,我们对BFS算法在高通量计算机上的性能进行了系统的评估.对于顶点规模为230的大图,在性能方面,高通量计算机在单节点的平均性能为24.26 GTEPS;在性能功耗比方面,高通量计算机的结果为181.04 MTEPS/W,在2019年6月发布的Green Graph500面向大数据集的排行榜上可以排名第2位[17].与通用的x86服务器相比,高通量计算机在单节点具有1.18倍的性能优势以及2.51倍的性能功耗比优势.由于高通量计算机的高并发、强实时和低功耗等特点,在处理大规模图数据时,结合应用特征采用新型的高通量计算机系统,可获得更高的处理能效.3 BFS算法优化
3.1 基于块查找的位图访问


3.2 Bottom-up遍历优化

4 实验结果与分析

4.1 高通量计算机介绍
4.2 优化手段评估

4.3 扩展性评估

4.4 CPU性能分析
4.5 性能对比

表7 高通量计算机相比x86服务器的性能加速比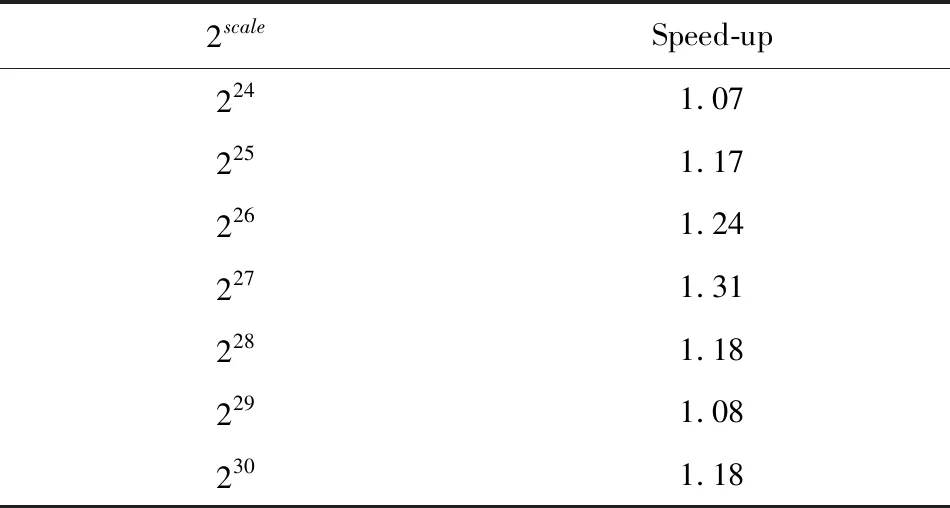
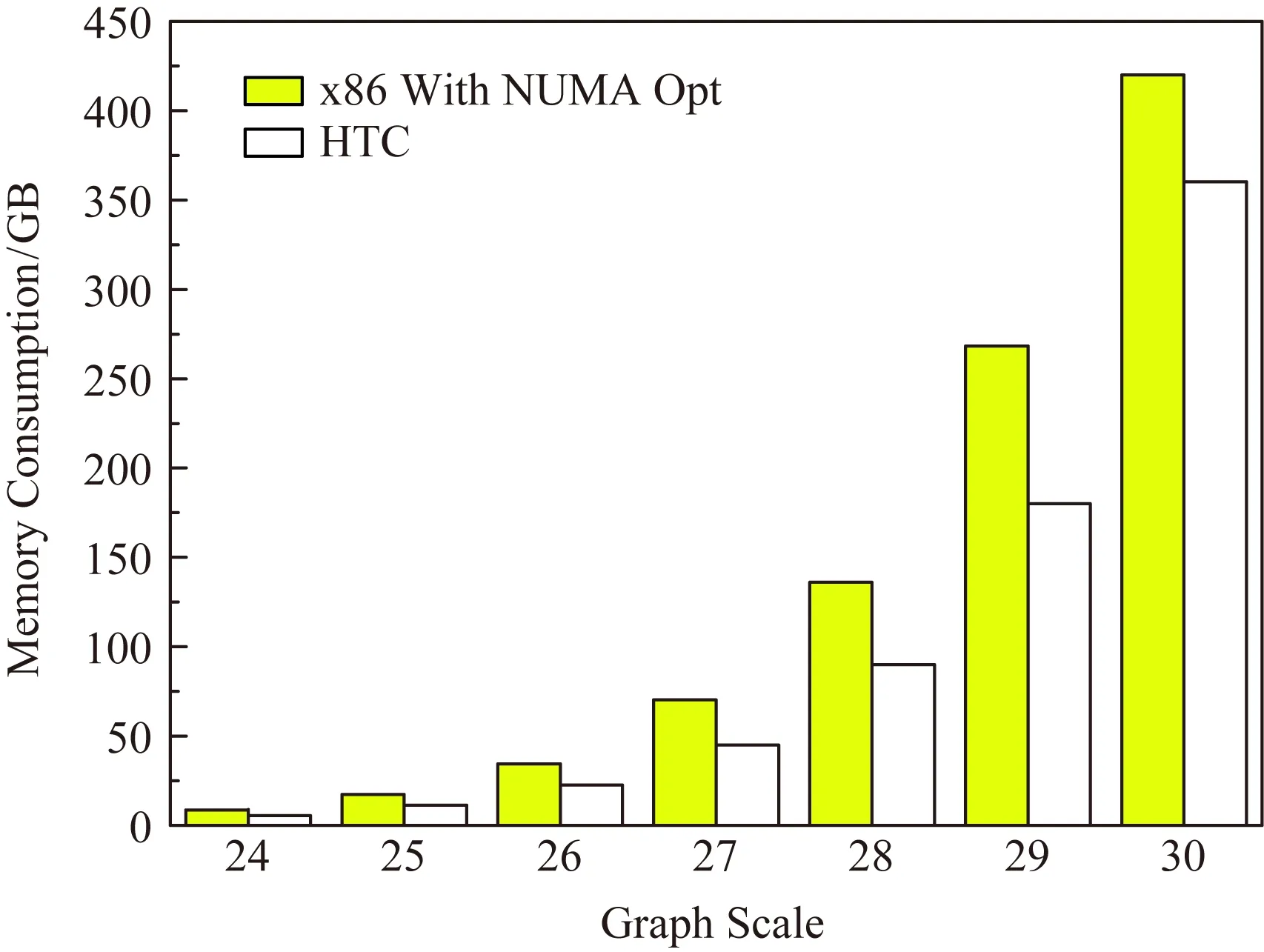
4.6 性能功耗比

5 总 结
