基于枢纽点流量控制的轴辐式物流网络优化

2020-06-23马瑞光

商业经济研究 2020年12期

马瑞光

（深圳市逸马商业科技有限公司广东深圳 518000）

引言

轴辐式网络（Hub-and-spoke network）的概念起源于航空网络规划，其指的是将一个或者几个机场作为枢纽点（hub），通过枢纽点进行中转衔接完成航空布局，同时机场周边较小的城市不通航，即为非枢纽点（Spoke）。目前，轴辐式网络结构已经广泛应用于军事、邮政、通讯、旅游等行业中，实践证明，轴辐式网络具有优化资源配置、提高运输效率、产生规模经济等作用。在轴辐式网络中，非枢纽点上的流量首先要汇集到枢纽点，然后再由枢纽点分配到网络上的其他点。由于枢纽点汇集了其他非枢纽点的流量，因此其产生了规模效益，降低了物流成本。但是在实际情况中，每个枢纽点都存在最大的流量处理能力，如果集中到枢纽点的货流量超出了枢纽点的最大流量处理能力，那么就会导致枢纽点出现拥堵，这就影响了货物的正常运输，增加了成本，降低了边际效益。所以要结合枢纽地的流量处理能力，考虑枢纽点数量以及位置，即考虑枢纽点的流量限制下进行轴辐式网络优化是很有必要的。

文献综述

目前，在轴辐式网络的拥堵研究和轴辐式网络模型的算法方面，国内外学者进行了相关研究。在轴辐式网络的拥堵研究方面，杨斌，邓志慧，胡志华（2016）在考虑了Hub拥堵成本的情况下，构建了最小化运输成本、建设成本和拥堵成本的非线性规划模型，并以此进行了验证；林天倚，卢春霞（2013）综合考虑了海运网络枢纽港的流量负担和成本，构建了基于拥堵控制的轴辐式海运网络枢纽模型，并使用拉格朗日松弛算法对模型进行求解；王卉（2013）首先把混沌粒子群算法应用在无容量限制的轴辐式航空网络设计中，然后加以调整，考虑了枢纽点流量上的拥堵成本，最后结合航空运输需求不确定性的特点，建立了需求不确定的枢纽航线网络优化模型；翁克瑞（2012）考虑了轴辐式网络中的固定轴线成本，建立了该问题的混合整数规划模型，并考虑了O-D流的绕道约束问题；Campbell（2009）对p枢纽中位问题、无容量限制的枢纽位置问题、枢纽覆盖问题以及p枢纽中心问题进行建模分析，并在枢纽中位问题中考虑了航线的轴线容量限制、枢纽节点限制以及航线的开辟成本等。在此基础上，其他学者对轴辐式模型进行了扩展，O’Kelly、Skorin-Kapov、Bryan（1996）探讨了当枢纽建设成本以及轴线运输成本折扣发生变化时，单分配和多分配的P枢纽中位问题的相应变化规律；S.A.ALUMUR（2012）研究了交通运输方式不确定性的情况下的枢纽网络设计问题；R.C.LEACHMAN（2011）基于排队理论预测了港口枢纽的流量和拥堵时间之间的关系，建立了基于货量、人员和装备的模型，并以中美之间的集装箱运输数据进行实证研究；L.FAN（2012）建立了多式联运网络，对集装箱运输的货量以及拥堵量进行了研究；CHEN G（2013）提出了船舶时间窗口的概念，并利用该概念处理口岸拥堵的问题。

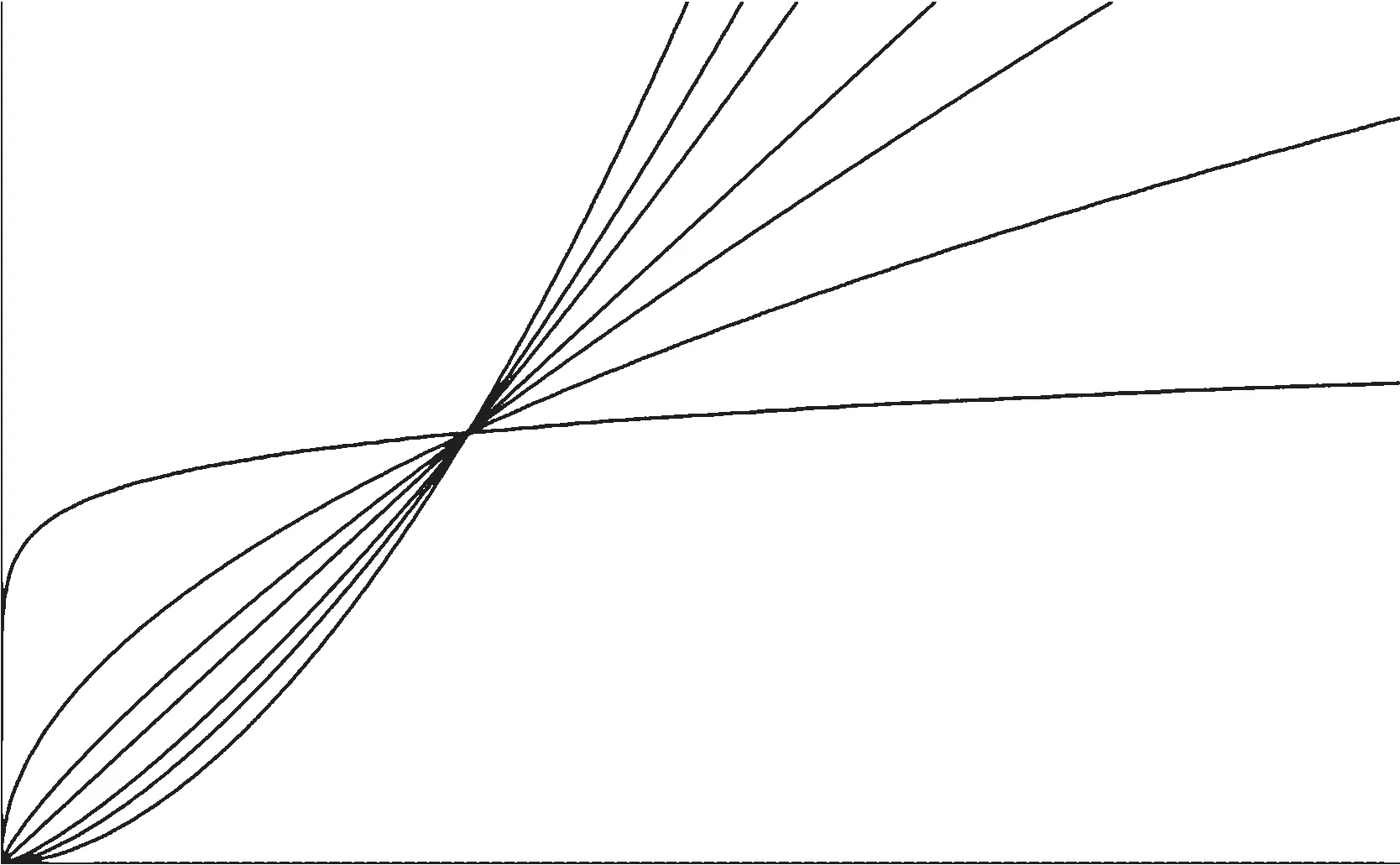
图1 不同a值时的变动成本函数图像

在轴辐式网络模型的算法方面，傅少川（2012）对轴辐式网络进行了优化，建立了单分配多枢纽中位问题模型，并利用改进的禁忌搜索算法进行求解；柏明国（2008）在多重分配多枢纽中位问题中利用禁忌搜索算法的启发式算法来进行求解；熊焱，王静慧（2012）利用混合遗传算法来求解货运轴辐式网络模型；付江月，陈刚（2015）针对轴辐式城市物流网络模型设计了带精英策略的自适应遗传算法；Marcos 和Cunba（2009）利用多初始解的禁忌搜索算法来求解单分配枢纽问题；Iwasa， Saito 和Matsui（2009）利用确定型迭代算法和随机型迭代算法来解决单分配问题；Klincewicz（1992）使用贪婪随机搜索算法和禁忌搜索算法来求解P-枢纽中位问题。

考虑到枢纽点的流量控制，本文首先考虑了基于流量控制可能会出现的变动成本，然后建立了优化后的轴辐式物流网络模型，并采用禁忌搜索算法进行求解，最后通过算例来比较优化后模型的合理性和有效性。

模型的建立

（一）枢纽点容量限制的成本函数

在轴辐式网络中，非枢纽点需要通过枢纽点进行连通，虽然轴辐式网络可以形成规模经济，但这也意味着会有大量的流量通过枢纽点，考虑到枢纽点流量控制的情况，可以用基于流量的枢纽点的成本函数来表示枢纽点的容量限制情况。枢纽点的成本函数包括固定成本和变动成本。固定成本是指建设枢纽点之初所进行的固定投入，例如设备、人工、机械等；变动成本是指随着经过枢纽点的流量而不断增加的费用，变动费用和经过枢纽的流量成正比。当较多流量汇集在枢纽点时，会直接导致变动成本的显著增加。则成本函数的参数设置如下：

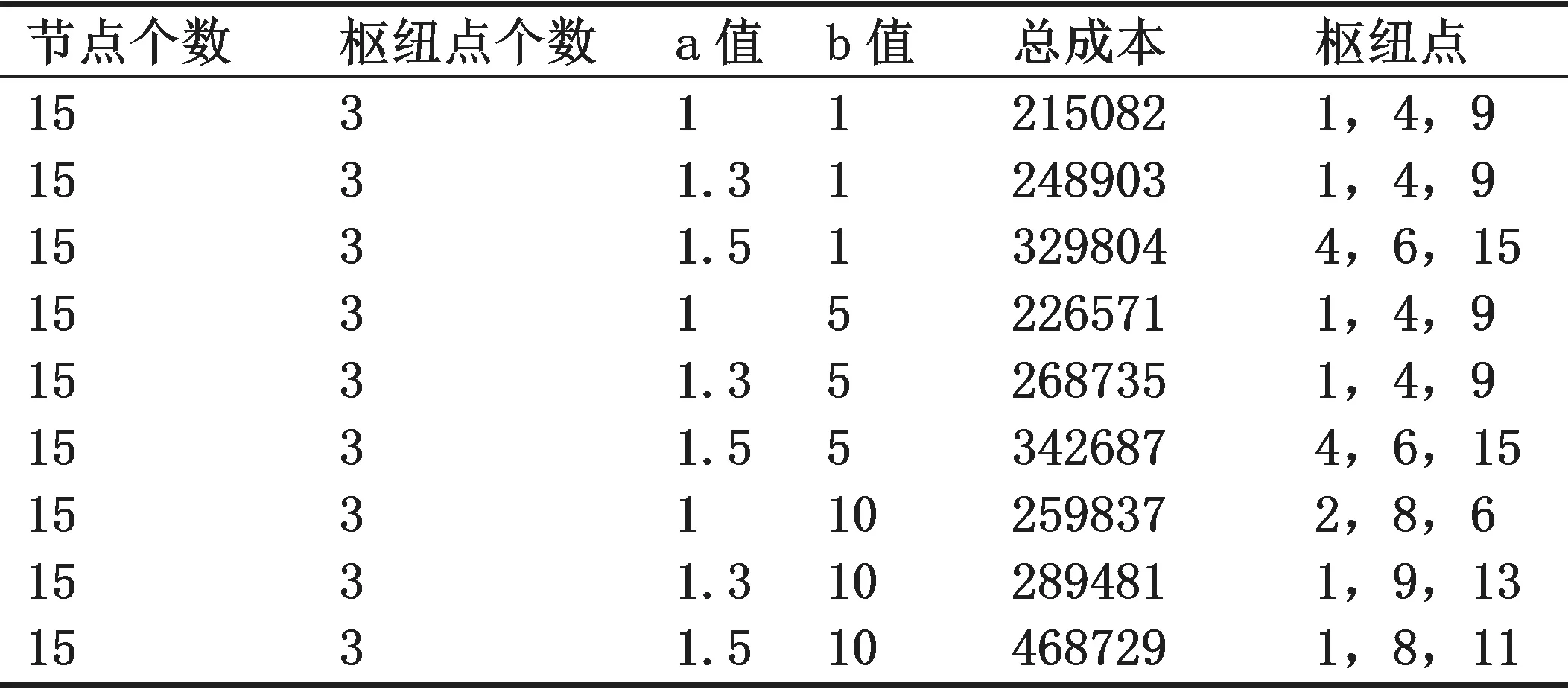
表1 a、b的值对最小总成本的影响

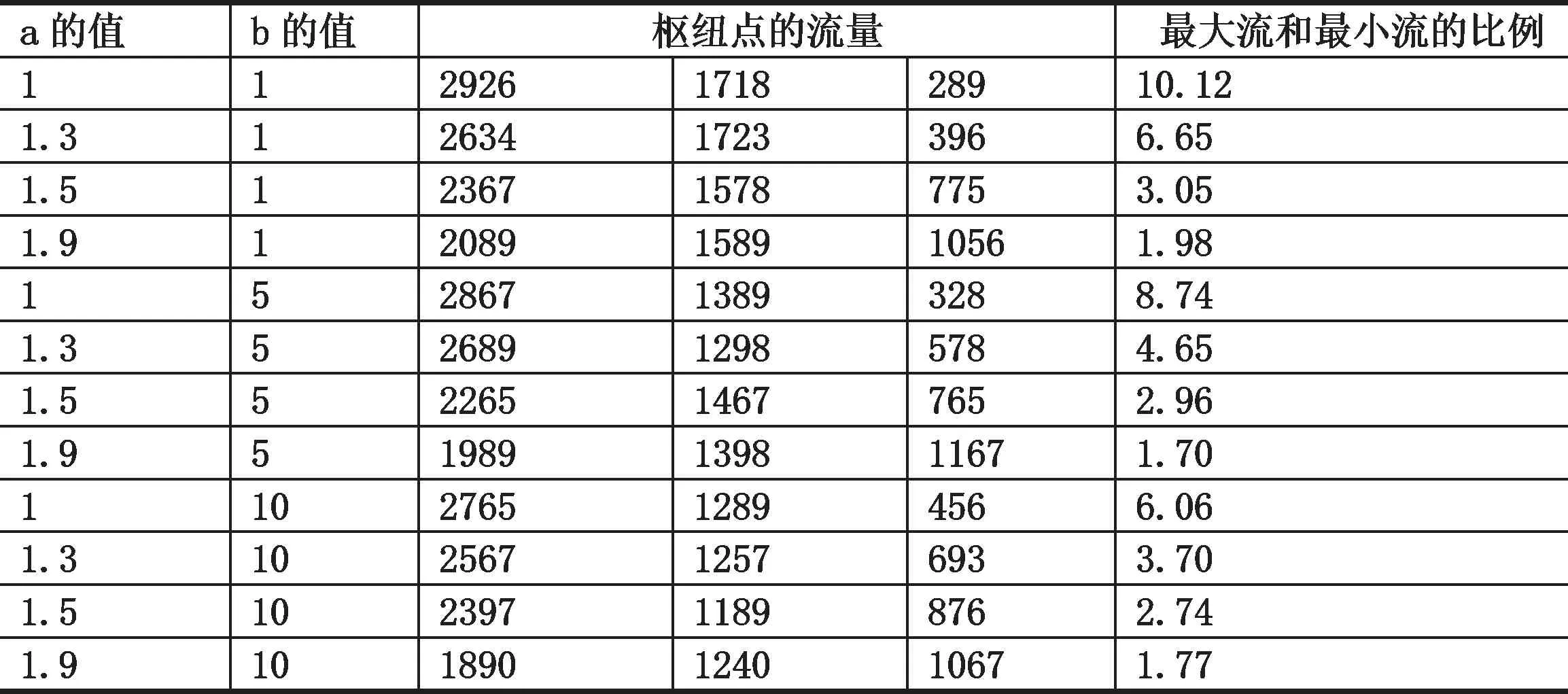
表2 a、b的值对枢纽点的流量的影响

G：固定成本；

w：流经枢纽点的流量。

变动成本随着枢纽点之间的流量的增加而增加。当枢纽点的流量小于安全值时，变动成本小幅缓慢上升；当枢纽点的流量超过安全值时，变动成本急剧上升。故呈现指数变化的情况，变动成本和流量之间的关系可以用以下幂函数来表示：

F(w)=bwa

f（w）表示枢纽点的变动成本，在这种情况下，a为大于0的数，当b=1时，a取不同的值时的变动成本如图1所示，其中y轴是变动成本，x轴是枢纽点流量。

由于枢纽点的建设存在固定成本，则枢纽点的成本函数为：

F(w)=f(w)+G=bwa+G

（二）考虑到枢纽点成本的轴辐式网络模型

在考虑到枢纽点成本的情况下，轴辐式网络模型优化的目标是确定枢纽点的位置，降低总成本，并优化轴辐式网络中的流量。该优化模型建立在一个具有N个节点的轴辐式网络中，有P个枢纽点，k、m为枢纽点，i、j为非枢纽点，具体参数设置如下：

wkm：枢纽点k、m之间的流量；

wijkm：从i点出发，经过k、m到达j点的流量；

Oi：流出节点i的流量；

Di：流入节点i的流量；

cik：节点i和节点k之间的标准单位运输成本。

该优化模型的假设条件如下：

（1）在轴辐式网络中具有N个节点，其中枢纽点为P；

（2）枢纽点之间完全直连，而非枢纽点之间通过枢纽点连接；

（3）单个非枢纽点可以多个枢纽点进行连接；

（4）枢纽点之间的单位运输成本折扣系数为α，0＜α＜1。

在满足上述假设条件的情况下，模型的目标是使得轴辐式网络中的总运输成本和枢纽点之间的运输成本最少。则建立模型如下：

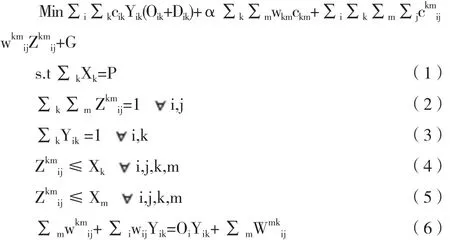
在此模型中，目标函数表示从非枢纽点i到枢纽点k、从枢纽点k到枢纽点m、从枢纽点m到枢纽点j以及枢纽点的固定建设费用最少。约束条件（1）表明选取P个枢纽点；约束条件（2）表示非枢纽点之间必须通过枢纽点才能够连接；约束条件（3）表示轴辐式网络中的节点只能作为轴点或者辐点存在，不能单独存在；约束条件（4）（5）表示只有当k、m点为枢纽点时，从非枢纽点出发的流量才经过k、m点；约束条件（6）表示只有i点的流量平衡约束。在目标函数中，枢纽点的成本可以用经过枢纽点的幂函数来表示，则目标函数可以表示为：

由于此模型属于非线性规划问题，故采用禁忌搜索智能算法进行求解。

模型的求解

本文采用禁忌算法求解。禁忌搜索算法的介绍。禁忌搜索算法属于一种智能算法，智能算法改变了传统的启发式算法依赖问题性质的搜索方法，其根据一定的规则来进行搜索，从而扩大了搜索的广度和深度，进而能够寻找全局最优解的目标。禁忌搜索算法的求解步骤包括初始解的选择、邻域的构建、禁忌表和禁忌长度、解的评价函数、特赦准则和停止准则。

算例分析

为了验证上述考虑到枢纽点容量限制的模型的合理性和有效性，本文使用算例进行研究，数据选择2012年中国十五城市的客流量以及航段距离，并使用禁忌搜索算法，通过JAVA编程进行求解。

（一）考虑枢纽点的拥堵对总成本的影响

通过JAVA编程，现通过改变a、b的值来确定枢纽点，以及分析枢纽点的总成本的变化，分析当枢纽点确定时的总成本的变化，在这种情况下，确定p=3，折扣系数α=0.6，在这种情况下模型运行结果如表1所示。

通过分析可知，当a、b取不同的值时，随着a的值增加，其最小总成本也在增大，说明枢纽点之间的流量成本增加了总成本；随着b值的增加，其总成本也增大，但增大幅度小于a增加时总成本增加的幅度，这说明相比于b，a的值对总成本的影响较大。

（二）考虑枢纽点的拥堵对枢纽点流量的影响

在已知枢纽点的个数和折扣系数的情况下，枢纽点的个数为3，折扣系数α为0.6，通过取不同的a和b的值，来分析a、b的取值对枢纽点的流量的影响，具体如表2所示。

通过分析可知，当a、b取不同的值时，随着a的值增加，枢纽点的最大流量和最小流量的比例逐渐变小，说明当考虑了枢纽点的流量控制时，一部分流量被进行了分流，从一个枢纽点分到了另外的枢纽点，从而使得整体的货流之间比较平衡。两个表经分析可知，当考虑了枢纽点的流量控制时，会导致总体的运输成本升高，但对整体网络的有益之处就是可以平衡枢纽点之间的流量。