去中心基于属性不可否认签名*

魏 亮，黄振杰，陈群山

(1.福建省粒计算及其应用重点实验室(闽南师范大学)，福建 漳州 363000; 2.闽南师范大学计算机学院，福建 漳州 363000)

1 引言

基于属性密码学，简称属性密码学，可提供细粒度和灵活的访问控制，因而受到广泛关注，成为近年来密码学研究的热点之一[1]。基于属性签名ABS(Attribute-based Signature)，简称属性签名，是属性密码学的重要组成部分。属性签名除了与属性加密一样可以进行细粒度访问控制之外，还具有通常数字签名所不具备的隐私性(Privacy)[2]。

2005年,Sahai等[3]开始研究属性加密，之后2008年,Maji等[2]开始研究属性签名，他们给出了属性签名的概念和安全模型。Maji等[2]提出的属性签名方案是针对单调访问结构的，2014年Okamoto等[4]提出了非单调谓词的属性签名方案，并在标准模型下证明是安全的。2016年，Sakai等[5]提出一般逻辑电路谓词的属性签名方案，可适用于任意访问结构。2019年，Datta等[6]提出了签名策略为无界算术分支程序的属性签名方案。还有一些增加了额外性质的属性签名方案，如基于属性的外包[7]、可链接[8]、层次[9]、可撤销[10]、代理[11]和动态门限[12]签名方案等。

在一般的属性签名方案中，存在一个唯一的属性权威中心。一旦权威中心出现腐败，整个系统就没有安全性可言了。作为一种解决方案，学者们提出了多权威机构属性签名MAABS(Multi-Authority Attribute-Based Signature)[13]的概念。在MAABS中，系统将属性交由不同的权威机构管理，大大减轻了单个权威中心的负担，但依然存在一个特殊的权威中心负责给其它权威机构发放密钥，如果这个权威中心出现腐败，仍将威胁整个系统的安全性。Okamoto等[14]更进一步提出去中心属性签名DABS(Decentralized Attribute-Based Signature)的概念。在DABS中，不再有特殊的权威中心，多个权威机构地位平等，独立为用户分发自己管理的属性密钥。一个权威机构出现腐败，只影响相应属性的安全性，其他属性的安全性仍不受威胁。2013年，Okamoto等[14]提出了第1个去中心属性签名方案，并在标准模型下证明了该方案的安全性。2014年，Kaafarani等[15]提出去中心可追踪属性签名方案，对安全模型进行了重新定义，增强了安全性。在文献[15]的基础上，2015年,Ghadafi[16]提出了更高效的去中心可追踪属性签名方法。2017年，Sun等[17]提出安全的去中心外包属性签名，大大降低了签名过程中的计算量。2018年,Sun等[18]将去中心属性签名应用于构建医疗区块链。

通常的数字签名是公开可验证的，任何人都可以使用公开信息来验证签名的真伪，这对某些文件的签署与发布是非常有利的。但是，在某些场合，签名人并不希望其签名被任意传播，比如对敏感消息的签名。为解决这个问题，1989年，Chaum等[19]提出了不可否认签名(Undeniable Signature)的概念。不可否认签名的特点是如果没有签名人的参与，其他人无法单独验证签名，也无法向第三方证实签名是真的。不可否认签名的经典应用场景是正版软件销售[19]，软件供应商在销售软件时需同时发放正版证书。如果正版证书是用通常签名算法签发的，那么恶意的客户就能私自复制出售附有正版证书的软件。如果正版证书改用不可否认签名算法签发，那么虽然恶意客户仍能复制软件和证书，但却不能向第三方证实证书的有效性(即不能证明软件是正版的)。2004年，Libert等[20]研究了基于身份不可否认签名；2008年，Duan[21]研究了无证书不可否认签名。虽然属性签名的研究已有十多年，但据作者所知，至今未见基于属性不可否认签名的研究报道。文献[22,23]虽称研究“基于属性的不可否认签名协议”，实则研究的是如何追踪属性签名的签名人，使其不能否认签名行为，令其对签名负责，这与可追踪性(Traceability)比较接近[24]，与Chaum等[19]提出的不可否认签名是完全不同的。

本文将基于属性、不可否认和去中心3个概念相结合，研究去中心基于属性不可否认签名。引进基于属性和去中心的性质，可以很大程度扩展不可否认签名的应用范围。仍以正版软件销售为例，使用基于属性不可否认签名可以让软件生产商对软件代销商进行细粒度控制，为每个软件指定代销商的资质要求，使得只有满足资质要求并且得到授权的代销商才能签发正版证书。使用去中心系统则可以做到不同的资质由不同的管理机构来颁授，而且这些管理机构可以不是软件生产商。

本文给出去中心基于属性不可否认签名的定义和安全模型，并构造一个去中心基于属性不可否认签名方案。该方案主要基于Cramer等[25]的证据隐藏零知识证明协议。本文选择Schnorr协议[26]作为其基础Σ协议，使用Shamir(t,n)门限方案[27]作为其秘密分享方案；再使用Fiat-Shamir转换[28]得到一个基础(t,n)门限签名BTS(Basic Threshold Signature)方案;然后再对BTS方案进行不可否认、防共谋和去中心化处理；最后得到一个去中心基于属性不可否认签名方案。在去中心属性密码中，防共谋的通常做法是引入用户全局标识，本文沿用这个做法。

2 预备知识

2.1 困难性问题

(1)离散对数问题DL(Discrete Logarithm problem)：假设G为大素数p阶循环群，g为G的生成元(下同)。给定群G中的随机元素A，计算a∈Zp，满足ga=A。记a为DL(A,g)，称A为关于g的离散对数。

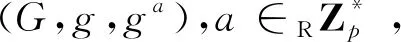
2.2 拉格朗日插值多项式

已知某个函数φ(x)在t个互不相同点xi(i=1,…,t)的函数值φ(xi)(i=1,…,t)，可构造t-1次拉格朗日插值多项式：

2.3 (t,n)门限签名方案

(t,n)门限签名方案是由文献[25]中Cramer等给出的一个用Σ协议构造证据隐藏零知识证明协议的方法构造而来的。如果选择Shamir(t,n)门限方案[27]作为其秘密分享方案，使用Schnorr协议[26]作为其基础Σ协议，再使用Fiat-Shamir转换[28]即可得到此签名方案。

基础门限签名BTS方案如下所示：

(3) Sign:不妨假设签名人拥有前t个私钥,对消息m∈{0,1}*进行签名：

③计算c=H2(m,R1,…,Rn)；

④用n-t+1个点(0,c),(t+1,ct+1),…,(n,cn)构造n-t次拉格朗日插值多项式Pn-t(x)；

⑤计算ci=Pn-t(i)，di=ti-cisi，i=1,…,t；

⑥输出签名：σ=(ci,di,Ri)(i=1,2,…,n)和多项式Pn-t(x)。

注：其中多项式也可不传，可根据签名中的参数重构，但会增加验证者的计算量。

(4) Verify:

①验证多项式Pn-t(x)是否为n-t次多项式；

②验证ci=Pn-t(i)，其中i=1,…,n，是否都满足；

③验证c=H2(m,R1,…,Rn)是否满足；

④验证Ri=gdiYici，其中i=1,…,n，是否都满足；

⑤如果上述条件都满足，则验证人接受此签名，否则不接受。

因为Schnorr协议和Shamir (t,n)门限方案满足文献[25]定理8的条件，所以由文献[25]定理8和Fiat-Shamir转换定理(文献[28]的定理4)，可得到如下引理：

引理1如果离散对数问题是困难的，则上述基础门限签名方案是存在不可伪造的。

引理2在上述基础门限签名方案中，签名所使用的私钥(证据)是隐藏的，也是不可区分的。

2.4 离散对数零知识证明

2.4.1 离散对数相等零知识证明[29]

EDLZKP(Equal Discrete Logarithm Zero Knowledge Proof)协议：

(3)P收到c后，计算d=r+cumodp，将d发送给T。

(4)T收到d后，检查gd=z1Uc和Vd=z2Wc是否成立。如果成立，则T接受P知道秘密值u，且DL(U,g)=DL(W,V)。

引理3上述协议具有如下性质：

(1)如果DL(U,g)=DL(W,V)，则验证人接受此证明有效。

(2)如果DL(U,g)≠DL(W,V)，则验证人接受此证明有效的概率是可忽略的。

(3)协议是零知识的，即通过此仿真算法任何人都可产生一个仿真副本，此副本与真实副本(按协议执行产生的)不可区分。

2.4.2 离散对数不相等零知识证明[29]

假设证明人P知道秘密值u=DL(U,g)，可使用下面的交互协议向验证人T证明DL(U,g)≠DL(W,V)。

NEDLZKP(No Equal Discrete Logarithm Zero Knowledge Proof)协议:

(3)P收到c后，计算d1=α+c(ur)modp，d2=β+crmodp，然后将(d1,d2)发送给验证人T。

(4)T收到(d1,d2)后，检查Vd1/Wd2=z1Ac，gd1/Ud2=z2是否成立。如果成立，则验证人T接受此证明。

引理4上述协议具有如下性质：

(1)如果DL(U,g)≠DL(W,V)，则验证人接受此证明有效。

(2)如果DL(U,g)=DL(W,V)，则验证人接受此证明有效的概率是可忽略的。

(3)协议是零知识的，即任何人都可通过仿真算法产生一个与真实副本不可区分的仿真副本。

3 去中心基于属性不可否认签名

3.1 去中心基于属性不可否认签名定义

1个去中心基于属性不可否认签名方案包含5个算法和2个交互式协议:

(1) Setup:输入系统安全参数1k，初始化系统公开参数gparam(下面各算法和协议都需要输入公开参数gparam，为简洁起见将其省略)。

(2) AAGen:每个属性权威机构Ai生成各自的公私钥对(pki,ski),ski为保密私钥，pki为公开公钥。

(3) UGen:用户产生自己的全局标识IDu。

(4) UAGen:属性权威机构Ai为用户生成关于属性Ai的私钥。输入用户全局标识ID、属性权威机构的私钥ski和属性Ai，输出用户私钥skID,Ai。

(5) Sign:输入签名人的私钥集{skID,Ai}、消息m和访问结构T，输出签名σ。

(6) Confirm:是验证人和签名人之间的交互协议。验证人输入四元组(ID,m,σ,T),签名人输入其私钥或某秘密值。如果签名是有效的，那么协议结束时，验证人接受该签名有效。

(7) Denial:与验证协议相似，验证人同样输入四元组(ID,m,σ,T),签名人输入其私钥或某秘密值。如果签名是无效的，那么协议结束时，验证人接受该签名为无效。

3.2 安全模型

去中心基于属性不可否认签名应具有正确性(Correctness)、不可伪造性(Unforgeability)、隐藏性(Invisibility)、属性隐私性(Attributes Privacy)和不可传递性(Non-transferability)等性质。

正确性是指，如果按方案给定的算法和协议执行，那么都将得到正确的结果。其定义比较平凡，限于篇幅，此处省略详细描述。下面给出其他性质的形式化定义。

3.2.1 不可伪造性

不可伪造性是指，如果没有获得满足访问结构所需的私钥，任何人都不能伪造有效的签名。其形式化定义通过如下的GAME 1给出。

GAME 1：

(1)挑战者C初始化系统，并公开公共参数gparam。

(2)C为各权威机构Ai生成公私钥对(aski,apki)，保留其私钥aski，并将公钥apki发送给敌手F。

(3)在多项式时间内，允许F适应性地进行以下询问：

①用户全局标识询问：F提交请求，C返回一个全局标识ID。

②用户秘密值询问：F提交IDu，C返回对应的秘密值su或⊥。

③密钥询问：F提交(Ai,ID)，C返回关于(Ai,ID)的密钥。

④签名询问：F提交(ID,m,T)，C返回关于(ID,m,T)的签名σ。

⑤验证询问：F提交(ID,m,T,σ)，C与之执行验证协议。

⑥否认询问：F提交(ID,m,T,σ)，C与之执行否认协议。

(4)最后，F输出(ID*,m*,T*,σ*)。

F赢得游戏，如果：

①(ID*,m*,T*,σ*)不能被否认。

②F没有对(ID*,m*,T*)进行过签名询问。

③F就ID*进行过密钥询问的属性集A*不满足T*。

定义1如果任意敌手F在多项式时间内赢得上述游戏的概率都是可忽略的，则一个去中心基于属性不可否认签名方案称为选择消息存在不可伪造的。

3.2.2 隐藏性

隐藏性是指，除了签名人外，任何其他人均不能判定签名的有效性。其形式化定义通过如下的GAME 2给出。

GAME 2

(1)系统初始化、权威机构公私钥生成同GAME 1。

(2)敌手F可以请求如同GAME 1的所有询问，挑战者C的响应也同GAME 1。

(3)F选择一条消息m*、访问结构T*和一个全局标识ID*，并提交给C。

(4)C接收(ID*,m*,T*)后，随机选择b∈{0,1}。当b=1时，计算(ID*,m*,T*)的有效签名σ*；当b=0时，从签名空间中随机选择σ*。将σ*发送给F。

(5)F得到挑战签名σ*后，还可进行预言机询问，但不能对(ID*,m*,T*,σ*)进行验证询问和否认询问，且就ID*进行过密钥询问的属性集A*不满足T*。

(6)最后，F输出其猜测b′。

如果b′=b，则称敌手赢得此游戏。

定义2如果任意敌手F在多项式时间内赢得上述游戏的概率是可忽略的，则称一个去中心基于属性不可否认签名方案具有隐藏性。

3.2.3 属性隐私性

本文沿用文献[14]的属性隐私性：由签名不能知道签名人拥有哪些属性。其形式化定义通过如下的GAME 3给出。

GAME 3：

(1)系统初始化、权威机构公私钥生成同GAME 1。

(2)预言机服务同GAME 1。

(3)敌手F选择目标明文m*、身份标识ID*、访问结构T*和2个满足T*的属性集(B0,B1)，将五元组(ID*,m*,T*,B0,B1)作为挑战目标提交给挑战者C。

(4)挑战者C收到(ID*,m*,T*,B0,B1)后,随机选择b∈{0,1}，然后用Bb的属性密钥产生签名σ*，并发送给F。

(5)F得到签名σ*后，还可以进行一系列询问。

(6)最后，F输出其猜测b′∈{0,1}。

如果b′=b，则称F赢得此游戏。

定义3如果任意敌手F在多项式时间内赢得上述游戏的概率是可忽略的,则称一个去中心基于属性不可否认签名方案具有属性隐私性。

3.2.4 不可传递性

不可传递性是指，在签名人向验证人证实或否认签名之后，验证人仍然不能向任何第三方证实或否认签名，但验证和否认协议的证据是不可传递的，即他不能从中得到任何知识以向第三方证实或否认签名。其形式化定义通过如下的GAME 4给出。

GAME 4：

(1)系统初始化、权威机构公私钥生成与GAME 1相同。

(2)预言机服务同GAME 1。

(3)敌手F向挑战者C提交挑战(ID*,m*,σ*,T*)。挑战者C随机选取b∈{0,1}。当b=0时，根据签名的有效性，C用仿真器(Simulator)产生一个验证或否认协议的副本；当b=1时，根据签名的有效性，C执行验证或否认协议得到一个副本。C将得到的副本返回给敌手F。

(4)敌手F可重复进行步骤(2)的询问。

(5)最后，F输出其猜测b′∈{0,1}。

如果b′=b，则称F赢得此游戏。

定义4如果任意敌手F赢得GAME 4的优势是可忽略的,则称一个去中心基于属性不可否认签名方案具有不可传递性。

4 去中心基于属性不可否认签名方案

本节提出一个去中心基于属性不可否认签名方案，其访问结构为(t,n)门限，具体如下所示：

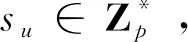
(5) Sign:不妨假设签名人S拥有的属性集为{A1,A2,…,At}。

ei=H1(Ai,ri,IDs,yi)

Ri=gdiYici

③计算:

c=H2(m,T1,T2,…,Tn,IDs)

④用n-t+1个点(0,c),(t+1,ct+1),…,(n,cn)构造n-t次拉格朗日插值多项式Pn-t(x)。

⑤计算ci=Pn-t(i)，di=ti-cisi，i=1,…,t。

⑥输出签名：σ=(ci,di,Ti,ri,IDs)(i=1,2,…,n)和多项式Pn-t(x)。

(6) Confirm:

①验证人T验证Pn-t(x)是否为n-t次多项式。

②验证是否有Pn-t(i)=ci，i=1,…,n。

③验证是否有Pn-t(0)=H2(m,T1,T2,…,Tn,IDs)。

④验证人T与签名人S进行交互验证。使用秘密值ss，签名人通过2.4节的EDLZKP协议向验证人验证DL(Ti,Ri)=DL(IDs,g)，其中Ri=gdiYici，Yi=riyiei，ei=H1(Ai,ri,IDs,yi)，i=1,…,n。

⑤以上全通过，则签名为有效签名。

(7) Denial:

①验证人T验证Pn-t(x)是否为n-t次多项式；

②验证是否有Pn-t(i)=ci，i=1,…,n；

③验证是否有Pn-t(0)=H2(m,T1,T2,…,Tn,IDs)；

④以上有一个不通过，则签名为无效签名。

验证人T与签名人S进行交互验证。使用秘密值ss，签名人通过2.4节的NEDLZKP协议向验证人证明存在某个i,使得DL(Ti,Ri)≠DL(IDs,g)，其中Ri=gdiYici，Yi=riyiei，ei=H1(Ai,ri,IDs,yi)。

注：上述方案是去中心的，方案中的每个权威机构都各自独立随机选取自己的私钥，然后计算自己的公钥，因此各权威机构的私钥是统计独立的。各权威机构都只知道自己的私钥，不知道其他权威机构的私钥，不存在掌握系统全部私钥的特别权威中心。如果某个权威机构被攻破或腐败，只影响相对应的一个属性的安全性，不会致使整个系统崩溃。

5 安全性与效率分析

5.1 安全性分析

定理1本文方案是正确的。

证明本定理可通过如下简单验算得到:

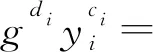
gtig-ci(ki+eiri)(gkigxiei)ci=

gti=Ri

□

定理2如果离散对数问题是困难的，那么本文方案是存在不可伪造的。

证明本文方案的不可伪造性可归约到预备知识2.3给出的基础门限签名方案(BTS)。详细证明过程如下所示：

如果存在一个敌手F能以εF的优势伪造本文方案的签名，那么存在敌手F′能以εF′=εF/q的优势伪造基础门限签名方案的签名，其中q为F请求用户全局标识的最多个数。记C为基础门限签名方案的挑战者。

(2)F′为所有权威机构Ai生成公私钥对(xi,yi=gxi)，将公钥yi和(G,p,g)发送给F，i=1,…,n。

(3)假设F最多请求q个全局标识，F′随机选取j,1≤j≤q。

(4)F′为F提供如下预言机服务：

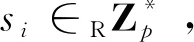
②当F对IDu进行秘密值询问时，如果IDu在IDlist中，F′返回su；否则，返回⊥。

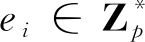
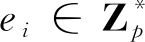
⑦当F对(ci,di,Ti,ri,IDs)(i=1,…,n)和多项式Pn-t(x)进行签名人验证或否认询问时，F′用ss与F进行验证或否认协议。

□

注：本定理的证明虽然是自适应选择属性和全局标识的，但也有个限制，即敌手攻击的全局标识是请求过全局标识询问的。因此，准确地讲，本方案是限制性自适应选择全局标识、自适应选择属性和自适应选择消息不可伪造的。“限制性自适应选择全局标识”还是要强于某些文献的“选定身份”或“选定属性”的。

定理3如果SDDH问题是困难的，那么本文方案具有隐藏性。

□

定理4本文方案具有属性隐私性。

证明在知识证明系统中，证据隐藏性是指在证明过程中，如果证明人等概率地使用证据w1或证据w2来进行证明，那么验证者猜中其所使用证据的优势是可忽略的。在属性签名方案中，属性隐私性是指，如果签名人等概率地使用属性集B0或属性集B1的私钥进行签名，那么验证者猜中其所使用私钥的优势是可忽略的。签名方案是一种特殊的非交互证明系统，属性隐私性与证据隐藏性两者的安全模型在本质上是一致的。本文方案是由Cramer等[25]的证据隐藏零知识证明协议经Fiat-Shamir转换[28]得到的，因此方案保持了证据隐藏的性质，用户所拥有的属性私钥就是其所使用的证据，从而具有属性隐私性。

□

定理5本文方案具有不可传递性。

证明根据定义4，如果存在能仿真出不可区分副本的仿真器则本定理成立。下面是分别给出证实协议和否认协议的仿真器。

(1)证实协议仿真器。

(2)证实协议仿真不可区分性：

从上述的仿真算法可知仿真副本的分布为：

从证实协议可知真实副本的分布为：

上述2个分布是相同的、不可区分的。

(3)否认协议仿真器。

(4)与否认协议真实副本不可区分：

否认协议仿真副本的分布如下所示：

否认协议真实副本分布如下所示：

上述2个分布是相同的、不可区分的。

□

5.2 效率分析

本文所提出的方案是基于属性不可否认签名方案，因目前未见同类方案的公开报道，因此只能与基于属性签名(不具有不可否认性)方案进行效率上的比较。目前，已有的基于属性签名方案大多是基于双线性对或多线性对的，只有文献[30，31，32]中的方案不是基于线性对的，其中文献[30]提出的是一种一般性构造方法，没有具体方案，无法进行效率比较；文献[31]所提出的方案不具有属性隐私性这一重要性质，从严格意义上说不能算是属性签名方案，因此也不具有可比性。文献[32]的方案与本文方案具有相同属性隐私性，也都不是基于线性对的，因此将本文方案与文献[32]方案作简单的效率比较，结果见表1，其中n为总体属性个数，t为签名人所拥有属性的个数，计算开销是指幂指数运算的次数，私钥、公钥、签名长度是指组成的元素个数。

可见，本文方案在签名计算、验证计算、签名长度、私钥长度方面都优于文献[32]方案。注意到文献[32]方案是基于RSA问题的，作者建议安全参数为1 024，而本文方案是基于离散对数问题，可以在椭圆曲线上实现，同等安全的安全参数为160，因此在数据长度方面的优势就更加明显了。在公钥长度方面，由于文献[32]方案是中心化的，所以只有1个权威中心的公钥，8个元素，约8×1024比特，而本文方案是去中心化的，n个属性就有n个属性机构，有n个属性机构就需要n个不同的公钥，约160n比特，在属性总体个数n小于50时，本文方案仍然具有优势。

Table 1 Comparision of efficiency and properties表1 效率性质对比

6 结束语

对基于属性签名的研究已有十多年，但仍未有真正基于属性不可否认签名的研究报道。本文将基于属性、不可否认和去中心3个概念相结合，研究去中心基于属性不可否认签名，给出了其定义和安全模型，并构造了一个去中心基于属性不可否认签名方案。这只是基于属性不可否认签名研究的初步探索，未来还需在功能更全、安全性更强、效率更高和签名长度更短等方面进一步努力。