基于改进BIRCH的双簇首WSN能耗优化研究*
2020-06-22罗擎忆王健敏
罗擎忆,张 江,张 晶,3,4,王健敏
(1.昆明理工大学信息工程与自动化学院,云南 昆明 650500; 2.中国船舶集团有限公司第七〇五研究所昆明分部,云南 昆明 650102;3.云南枭润科技服务有限公司,云南 昆明 650500; 4.昆明理工大学云南省人工智能重点实验室,云南 昆明 650500;5.云南省农村科技服务中心,云南 昆明 650021)
1 引言
随着无线传感器网络WSN(Wireless Sensor Network)的不断发展,其结构设计愈加成熟,应用场景也随之日益丰富。然而,由于其部署场景的复杂性、节点终端规模的限制性,一旦部署完成,为其进行能量补充以及更换的难度和成本将十分巨大。针对这个问题,许多研究人员对初始固定能源环境下,无线传感器网络的能耗均衡以及能耗优化问题进行了研究。
Heinzelman等[1]于2000年提出了被广泛学习和研究的LEACH(Low Energy Adaptive Clustering Hierarchy)协议。LEACH协议中,远离汇聚节点的簇首节点可能会因为长期保持远距离数据传输而致使自身能量过早耗尽,导致网络分割;此外,LEACH算法仅考虑节点之间的距离,未考虑簇首节点的能量状态,若剩余能量较低的节点被选取为簇首节点,该节点会加速死亡,从而导致整个网络生存时间缩减。
针对以上问题,学界发展了很多衍生算法来进一步优化和提升。其中一种思路是:由于不同簇与汇聚节点的距离不同,在多跳网络中,距离汇聚节点较近的簇首需要额外承担更多数据转发能耗[2]。为了避免因此出现的“热点”问题,众多基于距离变量的不均匀分簇协议被提出,该类分簇方法保证与汇聚节点距离较近的簇首能够将更多的能量用于数据转发。
之后,Li等[3]使用BIRCH(Balanced Iterative Reducing and Clustering using Hierarchies)聚类方法来改进LEACH协议,提出了LEACH-B算法。利用BIRCH聚类算法将整个无线传感器网络划分为若干个子域。由于BIRCH算法可以从多个维度进行划分,由此得到的子域相比传统分簇方法所划分的节点簇更加精准[4]。然而,他们的簇首选择仅仅考虑了单个子簇内部节点的能量剩余情况,没有对不同子簇之间通信能耗水平进行进一步的分析和约束。
石美红等[5]在双簇首的划分上与前者有着不同的思路,他们将传统簇首节点的通信职责一分为二:其一为内部通信簇首,用于接收子簇内非簇首节点所采集的数据并进行数据融合;其二为外部通信簇首,用于进行簇内数据发送和多跳网络的数据转发。通过将簇首的能量消耗进行分割,降低了单一簇首的能量消耗速率,使之与子簇内非簇首节点的能耗速率进一步接近[5]。但是,在进行簇首选择时,他们只考虑了子簇内部节点位置和剩余能量的影响,没有从传感器网络的宏观层面上对子簇的划分进行分析。
本文在文献[3,5]工作的基础上,提出一种基于改进BIRCH聚类的双簇首不均匀分簇算法—DHUCB (Dual Head Uneven Clustering based on BIRCH)。本文算法主要有以下创新点:
(1)采用改进的BIRCH算法从节点的剩余能量、节点距汇聚节点的距离、节点之间的距离3个维度对节点进行分簇,而不是仅仅从节点间距和剩余能量进行划分。以此将节点划分为基于距离向量的不均匀子簇。
(2)在进行双簇首选取时,同样使用上述3个维度进行选取概率计算,并分别使用独立的概率计算公式,使内外簇首能够根据工作特性进一步降低子簇内部能耗。
(3)使用概率队列机制,从簇首选取概率和内外通信簇首距离两方面对簇首进行选取——而不是直接使用概率最高的簇首——以保证双簇首策略选取函数的准确性。
最后,通过数据融合方法,从成簇的整个过程对子簇内部能耗进行处理。经实验验证,与文献[3,5]相比,在不同规模的传感器节点部署区域和不同规模的传感器节点数量环境中,本文算法在网络生命周期延长和节点能耗均衡的目标上,均有一定的提高。
2 系统模型
2.1 网络模型
本文中的无线传感器网络具有N个节点并部署在M*M大小的平面上,模型中仅考虑具有通信功能的节点。其他相关网络模型约束为:
假设1所有节点的初始状态相同,即具有相同电池容量,传输单位数据至单位距离所消耗的能量相同,计算单位数据的能耗相同;
假设2所有节点在系统中的任意一个阶段都不接受外部能量输入;
假设3系统中仅有一个汇聚节点,该节点的能量不做限制;
假设4系统中的所有节点(包括汇聚节点)的物理位置在整个生命周期中不发生改变。
2.2 能量消耗模型
本文所使用的能量消耗模型与文献[6-8]的相同。如图1所示,当系统传输kbit数据时,数据发送端的能量消耗为传输电路消耗和信号放大器的消耗;数据接收端的能量消耗为接收电路消耗。

Figure 1 Communication model图1 通信模型
图1中,ETX(k,d)为数据发送端的能耗,ERX(k)为数据接收端的能耗,Eelec为单位数据在发送电路上传输单位距离的能耗,εmp为单位数据在放大电路上传输单位距离的能耗。假定数据发送端与接收端的距离为d。定义一个阈值:
(1)
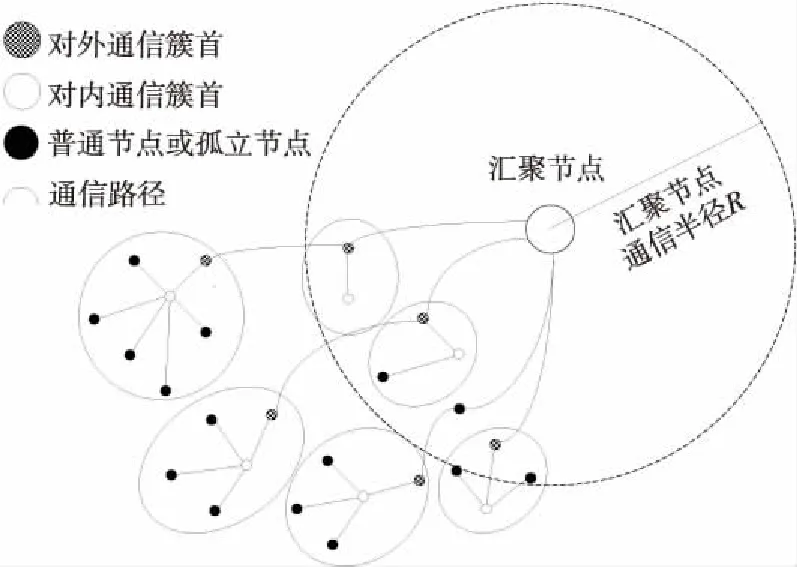
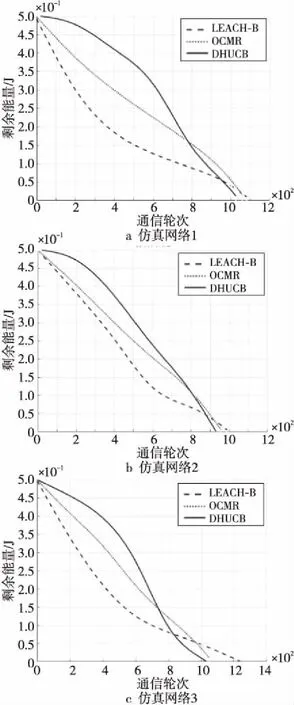
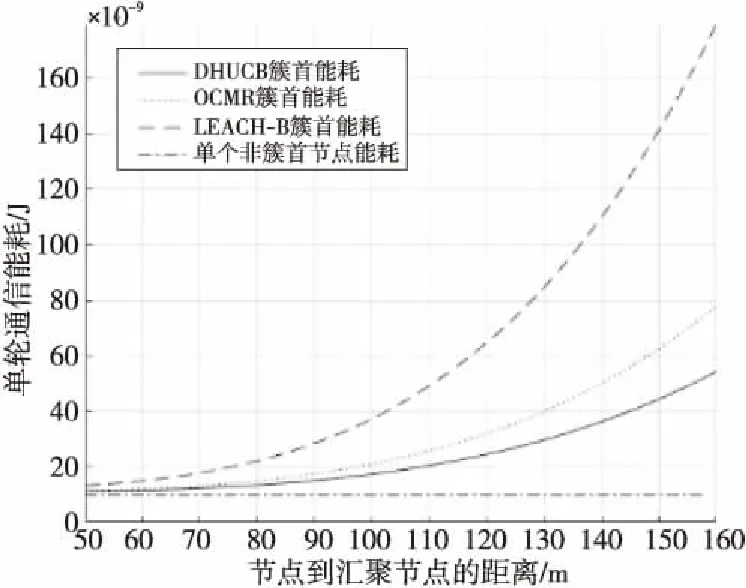
若通信半径r Table 1 Experimental simulation parameters表1 实验仿真参数 由图1所示模型可知,数据发送端发送kbit的数据至d距离的能耗为: ETX(k,d)=Eelec(d)+Eamp(l,d)= (2) 数据接收端接收kbit数据的能耗为:ERX(k)=k·Eelec。 本文中所使用的数据融合模型为任意子簇内的数据均被压缩到nbit,每次消耗能量EDA。 DHUCB算法分为3个阶段:(1)簇的划分,通过改进的BIRCH聚类进行节点划分,将整个无线传感器网络基于距离向量划分成簇内节点数不一的子簇;(2)簇首的选取,通过簇内节点剩余能量、簇内节点相对位置以及簇内节点相对汇聚节点的位置计算出内外通信簇首的概率队列,之后根据内外簇首距离确定簇首;(3)数据传输,对内通信簇首接收并融合非簇首节点采集到的数据。然后由外部通信簇首将这些数据通过多跳网络发送到基站。 3.1.1 聚类特征 BIRCH算法利用聚类特征对不同簇的信息进行约束。其基本定义如下所示: (3) 将其聚类特征CF定义为三元组(三维向量)CF={N,Σl,Σs},其中,N即为该簇的节点数,矢量 (4) 为各节点属性的线性和,标量 (5) 为各节点属性的平方和,xni为某个子簇中第n个节点的第i维属性。 由上述定义,可以推出定理1如下所示: 定理1设CF1={N1,Σl1,Σs1},CF2={N2,Σl2,Σs2}分别代表2个独立的聚类特征,将这2个聚类特征进行合并,合并后的聚类特征为: CF1+CF2={N1+N2,Σl1+Σl2,Σs1+Σs2} (6) 即聚类特征具有可加性。该定理的证明见文献[4]。 基于聚类特征,本文推导出如下统计量及距离: 质心为: (7) 半径为: (8) 直径为: (9) 其中,半径ρ是簇内节点到簇质心的平均距离,δ是簇内2节点之间的平均距离,他们都可以反映簇内节点的紧密程度。 (10) 3.1.2 聚类特征树 传统的聚类特征树(以下称CF树)有3个主要参数:枝平衡因子β、叶平衡因子λ和空间阈值τ。其中,β约束枝节点内子树节点的数量,λ约束叶节点内子树节点的数量,τ约束样本内所有CF树的最大半径。 在常规BIRCH算法中,空间阈值τ是常量,即,传感器网络中所有分簇的最大半径ρ的限定是一致的。然而,在多跳网络中,靠近汇聚节点的簇首会更多地进行数据转发。若对网络内所有子簇大小加以相同的散布约束,那么距离汇聚节点较近的外部通信簇首的能耗将会显著增大。针对这一现象,本文引入动态空间阈值的概念。 初始条件下,CF树的1个节点内仅包含内外通信簇首,包含2个网络节点,即τ0=2。预估下一阶段插入到CF树中节点的数量为: (11) 根据上一阶段已插入的节点数量和预估本阶段将要插入的节点数量,求出本阶段的一个空间阈值备选值为: (12) 利用半径ρ与Nc的关系,使用最小二乘线性回归估计出下一阶段网络中CF树节点的最大半径ρc+1的值,由此定义如下膨胀系数: (13) 使用贪心法找出密度最大的叶节点:对CF树按路径进行遍历,自顶向下找出包含子节点最多的叶节点后,计算该节点中距离最近的2个子节点之间的距离dmin。 与普通的单元树不同,CF树的节点为多元节点,即CF树的存储单元为包含一个至多个传感器节点的子簇。由定理1可知,CF树具有线性可加性,那么,当从树节点向其内部元节点观察时,有如下定义: 定义3CF树中任意节点中所包含的每一个传感器节点定义为一个元项E=[CFi,Si]。其中,CFi表示该节点上第i个子簇的聚类特征,Si表示指向该节点的第i个子节点的指针。 定义4本文中,CF树的高度为H,节点Ph,i为CF树第h层的第i个节点。其中,P1,i为第1层的第i个叶节点,PH,1为根节点。Nh,i为Ph,i内元项的数目,Eh,i,j为节点Ph,i的第j个元项。 由定义3和定义4得到任意元项Eh,i,j(h>1)的指针所指向的子节点为: (14) 3.1.3 CF树的构造 初始的CF树为空树。通过计算节点聚类特征的方式得到节点添加到CF树的具体路径。未加入CF树的节点从该路径插入到CF树中。其形成过程如下如下: 步骤1初始化。初始化CF树为空树,此时树的高度为0。 选择簇直径δ作为簇大小的散布统计量,以dic作为簇间距值。 步骤2从最优路径插入。确定当前需要插入的子簇C(单个节点也认为是一个子簇),计算其聚类特征信息。从根节点开始,逐层计算子簇C与CF树内任意一个子节点中的所有元项Eh,j,i(i=1,2,…,Nh,j)之间的距离,选出与子簇C距离最近的元项Eh,i,j*,他的指针所指向的子节点为: (15) 记录下步骤2中每层与子簇C距离最近的节点,所有节点依次连接,可以得到最优插入路径: I=I1,I2,…,IH-1= PH-1,iH-1,PH-2,iH-2,…,P1,i1 (16) 此路径长度为H-1。转步骤3。 ①若N1,i1<λ,则N1,i1=N1,i1+1,转步骤5。 ②若N1,i1=λ,分裂叶节点P1,i1,选出其内部距离最大的2个元项xα,xβ,以这2个元项为基础按dic划分余下元项,构成新的叶节点P1,i1和P1,i1+1,把原叶节点P1,i′(i′>i1)向后置为P1,i′+1,同时更新新叶节点的聚类特征和N1,i1、N1,i′+1的值,转步骤4。 (1)若Nh′,ih′<β,转步骤5 (2)若Nh′,ih′=β,参照N1,i1=λ的情况分裂Ph′,ih′: ①若h′ ②若h′=H,即Ph′,ih′是根节点,则上述分裂得到的新节点置为PH,1、PH,2,再为这2个节点添加一个新的父节点PH+1,1,此时NH+1,1=2且H=H+1;若待插入子簇C=∅,则结束构造,输出CF树,否则转步骤2。 (1)若h′=H,路径到达根节点: ①若待插入子簇C=∅,则结束构造,输出CF树; ②否则转步骤2。 (2)若h′ 3.1.4 簇的选取 本文中,由于需要对CF树的构造进行实时更新,其最大高度为: H′=log2(N+1) 选取CF树所有叶节点作为分簇结果,以得到对整个簇内的节点最为充分的划分。 在簇首选择阶段,本文从每个簇中选择2个簇首——一个是内部通信簇首,用于聚合簇内非簇首节点所采集的数据并进行数据融合;另一个是外部通信簇首,用于将内部数据通过多跳网络传输到汇聚节点,以及传输多跳网络中其他子簇的数据。 簇首的选择基于以下4个约束条件:节点的剩余能量、节点与汇聚节点的距离、节点与簇内其他节点的距离、2个簇首之间的距离。 首先,对节点的剩余能量进行考察,保证子簇中能量较高的节点有更高的概率被选为簇首。由式(2),数据发送端发送数据消耗的能量与发送端和接收端的距离d呈正相关,则在任意子簇内,距离汇聚节点越近的节点发送数据至汇聚节点所消耗的能量越少,因此对汇聚节点与传输节点的距离进行考虑。簇内数据传输所消耗的能量主要由以下2部分构成——(1)节点将数据传递至内部通信簇首的能量;(2)2个簇首之间传递数据的能量。因此,将子簇内各节点之间的距离和2个簇首之间的距离纳入衡量范围。 (17) (18) (19) (20) 使用上述式(18)~式(20)对式(17)中的变量进行进一步补充后,对式中的权衡常数因子{Qi}(i=1,2,3)的作用描述如下: 首先,对于内部通信簇首,节点剩余能量与簇内节点平均剩余能量的关系为关键因素,因此对其赋予最高的权值,设置Q1=0.5。节点与簇内其他节点的距离会显著影响数据收集所消耗的能量,所以赋给该参数以较高的权重,即Q2=0.4。但是,对于簇内通信,内部通信簇首节点不与汇聚节点进行直接的数据传输,因此子簇内节点与汇聚节点的距离在选择内部通信簇首时所占的比重较小,设置Q3=0.1。 其次,对于外部通信簇首,同样需要有较高的剩余能量。由于需要进行远距离传输,其能量消耗更甚于簇外通信簇首,因此赋予其权重为Q1=0.65。外部通信节点将数据传输到汇聚节点,因此,该节点与汇聚节点的距离占有较大权重,赋予Q2=0.35。而它与簇内其他节点的距离不会对外部通信能量消耗造成大的影响,相对赋予较小的权值Q3=0.05。 Figure 2 Communication cluster head election queue图2 通信簇首选取队列 算法1簇首选取 输入:内部簇首概率队列cur(q_i),外部簇首概率队列cur(q_o)。 输出:内部通信簇首IDid_i,外部通信簇首id_o。 步骤1cur(q_i) = 1,cur(q_o)=1; 步骤2 if(cur(q_i)→next== null &&cur(q_o)→next== null) cur(q_i) = 1,cur(q_o)=1; id_i= *cur(q_i),id_o= *cur(q_o);exit elsegoto步骤3 步骤3d_io=dist(*cur(q_i),*cur(q_o)); 步骤4 if(d_io id_i= *cur(q_i),id_o= *cur(q_o);exit else goto步骤5; 步骤5 dist_ei=dist(*cur(q_i),coc(i)); dist_eo=dist(*cur(q_o),coc(i));/*coc(centerofcluster)*/ if(dist_ei≤dist_eo) cur(q_o) =cur(q_o)→next; else cur(q_i) =cur(q_i)→next; goto步骤2。 上述簇首选取过程最大限度地保证了内外通信簇首之间的距离小于簇内节点的平均通信距离,即保证了内外通信簇首数据传输时所消耗的能量小于单簇首方案所消耗的距离。 经过3.2节的簇首选取后,汇聚节点向各子簇内的节点发送控制信息,包括向各个子簇发送簇首节点选取结果、向各个子簇发送其内部数据传输的时分多址TDMA(Time Division Multiple Access)方案、决定每一个外部通信簇首向外传输数据的下一跳地址。具体方案在本节进行讨论。 数据传输分为2个阶段:簇内数据传输阶段和簇间数据传输阶段。 簇内数据传输的过程中,在每一个TDMA周期内,子簇内节点收集环境中的数据,并在属于它的时间片内将数据传输给内部通信簇首。内部通信簇首将收集到的信息进行融合,并将融合数据发送给外部通信簇首。所有节点都完成一轮传输后,簇内数据传输阶段完成。 在前一阶段结束后,开始进行簇间数据传输阶段。外部通信簇首所传输的数据包括2个部分:(1)自身子簇内收集的信息;(2)其他外部通信簇首所发送的多跳数据。基于簇首的位置,其数据传输可能采取单跳传输也可能采取多跳传输。汇聚节点按照一定次序要求外部通信簇首发送数据。被选中簇首基于以下原则决定采用何种传输策略: (21) 当采取多跳传输时,采用以下方法选择下一跳目标: (1)选取多个候选传输节点,这些节点满足如下条件: ①候选节点与汇聚节点的距离小于该节点与汇聚节点的距离; ②候选节点与该节点的距离小于d0。 (2)候选节点选择完毕后,使用式(22)来选择下一跳目标: (22) 本文中,η和φ分别取2和1。α的值由式(23)决定: (23) (24) 经过上述算法,本文构建了一种基于改进BIRCH聚类的双簇首传输方案,其框架如图3所示。 Figure 3 Algorithm framework图3 算法框架 该方案有以下几个优点:(1)BIRCH聚类是多维聚类,能够将节点的不同信息均纳入到聚类因素中;(2)BIRCH聚类为不均匀聚类,在添加距离因子后,可以控制不同距离下子簇的大小,避免出现“热点”问题;(3)相较于传统的主副簇首策略和内外簇首策略,使用簇首选取队列保证了单轮次中簇首节点能量消耗的降低;(4)减少了数据传输过程中的能量消耗。本文算法的时间复杂度为O(N2),N为网络节点数量。 实验环境为Matlab 2016a软件,在1台主频为2.2 GHz的Intel®CoreTMi7 CPU,16 GB RAM的机器。采用了多种方式与文献[3,5]中的OCMR、LEACH-B算法进行对比,以测试本文算法在提升无线传感器网络WSN生命周期、均衡网络能耗上的表现。同时,也对实验结果进行了分析,以验证实验结果与理论分析是否一致。 本文的仿真参数如表1所示。 为了尽可能减小数据的随机性对算法性能稳定性的影响,本文的所有实验均进行了50轮节点随机坐标分布的仿真实验,取其均值作为仿真实验结果。通过与对比算法在首节点死亡轮次(FND)、半数节点死亡轮次(HND)和最终节点死亡轮次(LND)3个指标上的表现进行比较,综合网络能量消耗趋势对比,说明本文算法在提升网络生命周期和节点能耗均衡性能上的效果。 4.2.1 存活节点数随通信轮次的变化 如表1所示,在进行仿真时,本文设置了3组不同的参数值。其中,仿真网络1与仿真网络2的部署区域大小以及汇聚节点位置不同,并且这2个参数的变化尺度均以100 m为基准,其他参数均一致,设为对照组A;仿真网络2与仿真网络3除节点数量不同外,其他参数均一致,设为对照组B。后续对比将以这2个对照组作为基准。 图4a~图4c分别展示了3个仿真网络在不同参数值下,存活节点数随通信轮次的变化趋势。 文献[9]指出,在存活节点数-通信轮次图中,存活节点的变化趋势对于评估网络能耗的均衡性具有重要的指导意义,从出现第1个死亡节点开始,若存活节点的变化曲线斜率越大,则表示该曲线所代表的算法所实现的能耗均衡效果越好。 Figure 4 Live nodes vs.communication rounds in different simulations图4 不同仿真网络中存活节点-通信轮次图 观察对照组A,相对于对比算法,DHUCB所代表的曲线的平均斜率明显大于对比算法的。此外,如表2所示,在半数节点死亡轮次的对比上,相较于对比算法,DHUCB算法的平均数值更接近于首个节点死亡的轮次。即本文算法的半数节点死亡速率更快。这2点均说明本文算法具有较好的能量均衡性。 如表2所示,对照组A中的2个对照项的仿真结果中,本文所述的DHUCB算法在首个节点死亡和半数节点死亡2个指标上的表现均优于对比算法。说明在不同大小的节点部署区域内,本文算法均达到了延长网络生命周期的目的。 Table 2 Experimental results of control group A表2 对照组A实验结果 观察对照组B,在节点数量不同的前提下,与对照组A的实验结果相似,本文的DHUCB算法在曲线平均斜率、半数节点死亡轮次和首节点死亡轮次关系的表现上依旧优于对比算法,即在不同节点数的无线传感器网络中,本文算法均能表现出较好的能量均衡性。 同样,如表3所示,在节点数量不同的前提下,本文算法在首个节点死亡和半数节点死亡2个指标上的表现依旧优于对比算法。说明在不同节点数量的WSN中,本文算法均达到了减少能量消耗的目的。此外,在节点数量增大的情况下,本文算法首个节点死亡轮次缩短的比例要明显小于2个对比算法的。这说明随着节点数量的增大,本文算法依旧达到了延长网络生命周期的目的。 4.2.2 剩余能量随通信轮次的变化 由4.2.1节所得出的结论,本文所述的DHUCB算法在减少能量消耗方面的表现应优于对比算法。本节将从各个参数组下的对照组的剩余能量随通信轮次变化的情况对该结论进行验证。同时,同文献[10]所述,本文所述的无线传感器网络生命周期定义为从网络起始状态到首个节点死亡出现的轮次所含的周期。 观察对照组A,即从图5a和图5b所示的仿真能耗可以发现,在2组对照实验中,在首个节点死亡之前,DHUCB算法的剩余能量均优于对比算法的。相对于仿真网络1,由于仿真网络2扩大了部署区域,3个算法的能耗水平均有所提高,但DHUCB相对对比算法在能耗水平表现上依然有不小的优势。 观察对照组B,即图5b和图5c所示的仿真能耗可以发现,在2组对照实验中,在首个节点死亡之前,DHUCB算法的剩余能量依旧优于对比算法的。相对于仿真网络2,由于仿真网络3的节点数量增加,系统通信能耗随之增加,3个算法的能耗水平均有所提高,但是DHUCB相对对比算法在能耗水平表现上依然有不小的优势。 Figure 5 Network residual energy vs.communication rounds in different simulations图5 不同仿真网络中剩余能量-通信轮次图 4.2.3 网络能耗随传输距离的变化 对比算法LEACH-B和OCMR采用的都是均匀分簇的策略,即各个子簇中的最大节点数约束是固定的。由于本文算法和对比算法均使用多跳网络进行数据传输和转发,相对于距汇聚节点较远的簇首节点来说,距离汇聚节点较近的外部通信簇首承担额外的数据转发能耗的概率较大,成为所谓的“热点”。节点自身能耗加大,造成网络整体能耗的不均衡。本文采用了3.1.2节所述的动态空间阈值策略,使得子簇中的最大节点数和子簇与汇聚节点的距离线性相关,子簇中簇首用于簇内数据传输的能量也更趋近于线性相关。 Table 3 Experimental results of control group B表3 对照组B的实验结果 Figure 6 Distance-Energy consumption per round图6 距离-单轮通信能耗 图6所描述的是仿真网络1在某一通信轮次中不同算法的簇首能耗随节点到汇聚节点距离的变化情况。同时,加入单个非簇首节点能耗与簇首能耗进行对比。 由图6可知,本文算法的簇首能耗随节点到汇聚节点距离的增长速率在3个算法中是最小的。这说明在一定程度上,本文算法相较于对比算法减轻了网络中不同区域簇首的能耗差异,部分解决了均匀网络的“热点”问题。此外,将簇首能耗与单个非簇首节点的能耗进行对比。本文算法的簇首节点能耗与非簇首节点能耗的差距在3个算法中是最小的,进一步说明本文算法在能耗均衡性上的效果较好。 4.2.4 算法计算能耗对比 在评价算法能耗时,算法本身的计算能耗也占据了较大的比重。若算法在执行能耗上进行了优化,但算法本身的运行能耗增加,则整个算法的整体能耗反而可能增大。由文献[11]可知,嵌入式软件的算法级能耗计算公式为: EA=(∑i(Bi×Ni)+Ti+Si)×L+Ej (24) 其中,Bi为指令i的基本能耗;Ni为指令i的执行次数;Ti为时间复杂度,Si为空间复杂度;L为软件的运行时间,Ei为算法中的其他能耗。在本文的评估中,不考虑机器性能的差异,可以将L设置为1,其他能耗包括DHUCB算法额外计算的内外簇首间的距离,计算出如表4所示的能耗数据。 从表4(由于3个算法的复杂度对于最终的能耗影响是一致的,因此进行总计时略去)可以看出,本文算法与对比算法的计算能耗基本处于同一水平。在进行能耗优化的同时,没有明显增大算法的计算能耗。 由上述仿真实验结果可知,本文DHUCB算法在不同节点数、不同节点部署区域情况下,均能达到优于对比算法的能耗均衡能力,且能耗减少效果较好,基本达到了前述章节的理论分析所推导的关于网络生命周期延长效果和节点能耗均衡的结果,并在一定程度上减轻了“热点问题”。在解决上述问题的同时,本文算法计算能耗未明显增大,本节的论述验证了本文算法的有效性。 本文提出的基于改进BIRCH聚类的双簇首不均匀分簇算法从节点的剩余能量、节点距汇聚节点的距离、节点之间的距离3个维度对节点进行分簇,对成簇过程中的数据维度进行了多方面的约束和分析。在此基础上,构建出一种基于四维信息的簇内双簇首的数据传输模型,并使用簇首队列的簇首选取模式以保证本模型在能耗优化上的稳定性,达到WSN的能耗均衡和生命周期提升的目的。经实验验证,在不同规模的传感器节点部署区域和不同规模的传感器节点数量环境中,本文算法相较于OCMR、LEACH-B算法在网络生命周期和节点能耗均衡上,均有一定的提高。 Table 4 Algorithm energy consumption表4 算法能耗对比 nJ 
3 算法实现
3.1 簇的划分




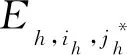
3.2 簇首的选取

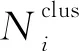



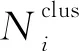



3.3 数据传输

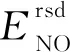
4 实验仿真
4.1 算法评价过程及指标
4.2 仿真实验结果


4.3 实验小结
5 结束语

