加权LOF结合上下文判断的云环境中服务运行数据异常检测方法*
2020-06-22仇开,姜瑛
仇 开,姜 瑛
(1.云南省计算机技术应用重点实验室,云南 昆明 650500;2.昆明理工大学信息工程与自动化学院,云南 昆明 650500)
1 引言
近年来,云计算技术迅猛发展。云环境中分布着海量服务,服务不是孤立存在的,服务与服务之间存在组合调用关系,这构成了复杂的服务运行环境。在复杂的云环境中,服务运行数据如果存在异常,将影响服务的运行,或演化为服务故障,甚至导致服务的宕机。2014年4月,Amazon EC2服务中断了100多个小时,导致交易系统关闭,造成700多万美元的损失[1]。2017年6月,苹果iCloud服务约有1%的用户持续宕机超过36 h,受影响用户无法使用之前的备份来恢复设备数据,造成了无法估量的经济损失[2]。如果云环境中重要的服务宕机1 h,由此导致的经济损失将以百万美元级别计算[3]。为了确保云环境下服务的正常运行,对云环境中的服务运行数据进行异常检测是亟需解决的问题。
2 相关工作
异常检测是指在数据集中发现与预期数据不符的离群点的过程[4]。目前,已有针对云环境中软件异常检测的方法,可以将其分为有监督的方法和无监督的方法。有监督的方法需根据一个已经标记的数据集训练出一个分类器,然后根据这个分类器,将测试数据划分到各类别。文献[5]提出了基于Cluster-KNN的方法用于检测网络异常,首先用K-means聚类算法划分数据,计算聚类中心的质心,然后再使用近邻搜索算法从聚簇中获取相应的k近邻,最后对k近邻使用基于KNN的近邻决策算法得出最终分类结果。文献[6]在SMO(Sequential Minimal Optimization)算法的基础上提出了具有在线学习能力的LASVM(Learning Active Support Vector Machine)算法,用于云环境异常检测,相比传统SVM算法,在海量数据集处理上有较快的处理速度,占用更少的资源。无监督的方法不需要有标记的数据集。聚类是一种典型的无监督方法,这种方法能够将相似的数据聚集到同一个簇中。LOF(Local Outlier Factor)算法[7]是一种基于密度的聚类算法,文献[8]提出了一种基于改进LOF的异常检测算法,用于云计算环境中的异常检测,算法提出用R-tree来存储每个点的k近邻,提高了算法的运行速度且具有较好的准确率。文献[9]提出了一种基于K-means的改进异常检测算法,用于云环境中虚拟机异常的检测,通过策略来设置初始聚类中心,并对聚类结果中心点进行修正,最终将虚拟机运行状态分为正常、异常和故障。
在上述异常检测方法中,存在以下问题:(1)部分方法对异常判断的准确率不高,例如文献[5,6,9]在计算距离时采取了传统的欧氏距离,未考虑数据的各个维度在求解距离过程中体现的不同作用,导致使用传统的欧氏距离来进行异常判断不够准确;(2)在异常检测中,只考虑服务运行数据本身的异常程度,而忽略了服务上下文信息,易将正常的服务运行数据划分为异常数据。在云环境中,存在大量任务调度,可以将这些任务调度视为服务的上下文信息,任务执行会导致服务的运行数据产生大幅度的变化,这些由于正常任务执行而产生波动的服务运行数据不能视为异常。针对以上存在的问题,本文提出了一种加权LOF结合上下文判断的云环境中服务运行数据异常检测方法,用于服务运行数据的异常检测。
3 加权LOF结合上下文判断的服务运行数据异常检测方法
在检测云环境中的服务运行数据异常时,为了提高异常判断的准确率,本文将异常检测分为2个阶段:首先,在进行初次异常判断时,为了区别对待服务运行数据各维度的属性值,本文使用信息熵赋权法对不同维度属性赋予不同的权值,并对LOF算法进行改进,使用了加权欧氏距离;然后,在二次异常判断时,将初次判断后得到的异常服务运行数据集与服务运行时的上下文信息进行综合判断,得到异常判断的结果。本文方法流程如图1所示。

Figure 1 Flow chart of anomaly detection method for service running data in cloud environment based on weighted LOF and context judgment图1 加权LOF结合上下文判断的云环境中 服务运行数据异常检测方法流程图
3.1 基于加权LOF算法的服务运行数据异常程度计算
本文进行的初次异常判断是为了计算云环境中服务运行数据的异常程度,为异常判断提供依据。服务运行数据的异常程度可以根据其局部异常因子的值来确定,数据局部异常因子的值可以通过LOF算法计算得到。由于LOF算法没有考虑到服务运行数据各维度在求解距离过程中贡献的差异,本文使用信息熵赋权法给服务运行数据的各维度属性赋予不同的权值,然后计算加权欧氏距离,使用加权LOF算法计算服务运行数据的异常值。
3.1.1 服务运行数据各维度属性赋权
信息熵[10]表示数据的不确定性,熵值越大,变量的不确定性就越大,其提供的信息量就越小;熵值越小,变量的不确定性就越小,其提供的信息量就越大。云环境中的服务运行数据是多维的,每个维度的数据的取值范围都存在差异,因此不同维度的数据含有的信息量不同,需要区别对待。
假设待判断的服务运行数据集RuntimeData={x1,x2,…,xn},下称RD,其中xi(1≤i≤n)是m维数据。服务运行数据集RD的各维属性赋权过程如算法1所示:
算法1各维度属性赋权算法
Input:服务运行数据集RD。
Output:权值集合W={w1,w2,…,wm}。
Step1使用Z-Score[11]标准化方法处理服务运行数据集RD得到RD′={x′1,x′2,…,x′n},用式(1)计算数据集RD′ 中第i个数据的第j维属性的比重Pij:
(1)
其中,1≤i≤n,1≤j≤m,x′ij是RD′的第i个数据的第j维属性值。
Step2用式(2)计算数据集RD′第j维属性的信息熵Ej:
(2)
其中,p=1/lnn。
Step3用式(3)计算数据集RD′中第j维属性的波动系数fj:
fj=1-Ej
(3)
Step4用式(4)计算第j维属性的权值wj:
(4)
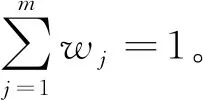
3.1.2 计算加权欧氏距离
通过算法1可以获得服务运行数据各维度属性的权值集合W。根据信息熵理论,这些属性之间的不确定性是不同的,服务运行数据中的异常点表现出的不确定性是由于其在某些属性上的取值范围不同造成的,服务运行数据各维度属性的不同权值实际上是其不确定性的一个反映。文献[8]中的LOF算法在使用欧氏距离时没有考虑属性之间的不确定性会影响异常判断的准确率。因此,本文使用式(5)[12]计算归一化后的服务运行数据集合RD中的任意数据xA和数据xB的加权欧氏距离WeightDis(xA,xB),下称WD(xA,xB):
(5)
其中,1≤j≤m,xAj为数据xA的第j维属性值,xBj为数据xB的第j维属性值,wj是第j维属性的权重。
3.1.3 筛选初步异常服务运行数据集
为了提高服务运行数据异常判断的准确率,使用3.1.2节中的加权欧氏距离替换文献[8]中LOF算法中涉及到的欧氏距离,改进的加权LOF算法如算法2所示:
算法2改进的加权LOF算法
Input:.经Z-Score标准化的服务运行数据集RD′={x′1,x′2,…,x′n},RD′的各维属性的权重集合W={w1,w2,…,wm}。
Output:初步异常服务运行数据集E。
Step1若数据集RD′所有数据都被处理,转Step 6;否则,从数据集RD′取出一个未经过处理的数据xA进行以下处理。
Step2求数据xA的第k加权近邻距离k-WeightDis(xA),下称k-WD(xA)。其中,k-WD(xA)为数据xA与数据集中其他数据加权距离大小排名(升序)为第k的距离。
Step3求数据xA的k邻域Nk(xA)和邻域中的每个数据xO到数据xA的加权局部可达距离WeightReachDis(xA,xO),下称WRD(xA,xO),其中Nk(xA)为数据xA与数据集中其他数据加权距离大小排名(升序)前k的数据的集合,WRD(xA,xO)=max{k-WD(xA),WD(xA,xO)}。
Step4求数据xA的局部可达密度lrdk(xA):
(6)
其中,|Nk(xA)| 是数据xA的k邻域中数据的个数。
Step5通过式(7)求数据xA的局部异常因子LOFk(xA),如果LOFk(xA)>LOFthreshold,将数据xA加入初步异常服务运行数据集E,转Step 1。其中,LOFthreshold为阈值,若数据的局部异常因子大于此值,该数据为异常;若小于或等于此值,该数据为正常。
(7)
Step6结束,输出初步异常服务运行数据集E。
经过以上步骤后,对服务运行数据进行初次异常判断,得到初步异常服务运行数据集E。
3.2 基于上下文信息匹配的服务运行数据异常判断
通过3.1节的方法对服务运行数据集进行了初步筛选,得到初步异常数据集。初步异常数据集只是服务运行数据自身的异常程度的反映,其中的部分异常数据可能是由于云计算服务运行环境中存在相关正常任务调度产生的,但这种因任务调度产生的“异常”并不是真正的异常。因此,需要在采集正常服务组合数据并获取其数据特征后,再对初步异常服务运行数据集进行二次异常判断。
3.2.1 服务组合数据处理
为了判断异常数据是否与云环境中的服务的运行环境相关,需要考虑相应的服务上下文信息。服务上下文信息是描述云环境中服务的环境状态、资源信息、用户需求的属性或属性值[13],可以用于辅助异常数据的判断。例如,对于某服务,t时刻的CPU和内存利用率是该服务的运行数据,t时刻的系统进程数是服务的上下文信息。因为上下文信息从侧面反映当前服务的状态,其与运行数据之间存在关联性,在异常判断时上下文信息起到辅助作用,因此需要综合考虑服务运行时的上下文信息。
为了综合考虑服务运行时的数据和当时的上下文信息数据,本文给出服务组合数据的定义:服务组合数据是同一时刻t,一条服务运行数据和一条上下文信息数据的组合,如式(8)所示:
Compt=(xt,yt)
(8)
其中,Compt是服务组合数据,xt是时刻t的服务运行数据,yt是时刻t的服务上下文信息数据。
同一类服务上下文信息数据,其对应的服务运行数据往往具有相同或者相似的特征。为了获取数据特征,可以在正常运行情况下采集服务组合数据后,首先使用K-means算法[14]对服务上下文信息进行聚类,使得具有相同或者相似服务上下文信息的数据被归于同一个簇,初始聚类中心的选取方法参照韩晓红等人[15]的选取策略。聚类完毕后可以获得每条组合数据的上下文信息簇号a和对应上下文信息簇的中心坐标Ca,1≤a≤kK-means,其中kK-means为K-means算法的初始聚类数。
对于在同一类上下文信息簇中的服务运行数据,需要为其建立正常服务运行数据集超球体。对于同一个簇,所有正常的服务运行数据都应该包含在超球体内部。每个上下文信息簇的正常服务运行数据集超球体构建算法如算法3所示:
算法3服务运行数据集超球体构建算法
Step1通过上下文信息簇号a,提取具有相同簇号a的服务运行数据集Da={h1,h2,…,hv|v∈N*},v是簇号为a的服务运行数据集的大小。
Step2计算数据集Da中每个数据和Ca之间的欧氏距离L,获取数据间的最大欧氏距离Lmax。
Step3以Ca为超球体球心,Ra=Lmax为超球体半径,构造簇a对应的服务运行数据集超球体Oa。
Step4结束。
经过以上步骤,为不同的上下文信息簇建立了不同的数据特征。其特征在于:不同服务上下文信息簇下的数据,若在其相应服务运行数据的超球体内,则该数据为正常;若在超球体外,则该数据为异常。不同簇的数据特征的建立为初步异常服务运行数据集的二次判断提供了依据。
3.2.2 二次异常判断
为了提高异常判断的准确率,对于每个初步异常数据,都需要获取其上下文信息,并将其与正常服务组合数据的上下文信息进行匹配。初步异常服务运行数据集数据点的二次异常判断如算法4所示。
算法4初步异常服务运行数据集数据的二次异常判断
Input:服务运行数据集RD的初步异常运行数据集E={xp,xq,…,xr},其中p、q、r等是初步异常服务运行数据集E中的数据在RD数据集中的对应序号。
Output:最终异常服务运行数据集F。
Step1F=E。
Step2若数据集中所有数据都被处理,转Step 6;否则,从数据集E中取出一个未经过处理的数据xu进行处理,其在RD数据集中对应的序号为u,获取初步异常数据集中下标为u的数据的组合数据(xu,yu),计算上下文信息数据xu与正常组合数据中上下文信息的每个簇中心点的欧氏距离M,根据最小距离原则,得到距离最近的簇的簇号a。
Step3计算初步异常服务运行数据xu与簇号为a的超球体中心点Ca的欧氏距离Lu。
Step4若Lu>Ra,则表明初步异常的服务运行数据不在超球体内,数据远离正常,最终该数据被判断为异常。
Step5若Lu≤Ra,表明初步异常数据的服务运行数据在超球体内,数据正常,最终数据xu被改判为正常,从数据集F中剔除数据xu,转Step 2。
Step6结束,输出最终异常服务数据集F。
本文提出的方法进行了2次异常判断,第一次使用加权LOF算法进行局部异常因子的计算,大于阈值的数据初步判断为异常。对于初步异常服务运行数据,其数据的波动可能是由上下文信息变化引起的,也有可能是真正的异常波动,因此需要对这些初步异常数据进行二次异常判断。首先将这些数据的上下文信息与正常服务组合数据的上下文信息簇匹配,再与最相似的簇内的服务运行数据超球体中心点求欧氏距离,若距离大于超球体半径,则是真正的异常数据;若距离小于或等于超球体半径,则初步异常数据被认为是正常数据。
4 实验与分析
4.1 实验1
为了初步验证本文方法的有效性,借助VMware 11虚拟化工具,使用OpenStack搭建基于Hadoop 2.7的云计算平台,包含3个节点(1个Master节点和2个Slave节点)。本文使用Java语言开发了一个加权LOF结合上下文判断的云环境中服务组合数据异常检测原型工具,其功能是监测MySQL服务和平台的基础设施服务的服务组合数据。
为获取云环境中的相关服务组合数据,本文将原型工具部署在Master节点上,采集运行时的MySQL服务组合数据和基础设施服务组合数据作为测试数据集,采集的数据内容如表1和表2所示。
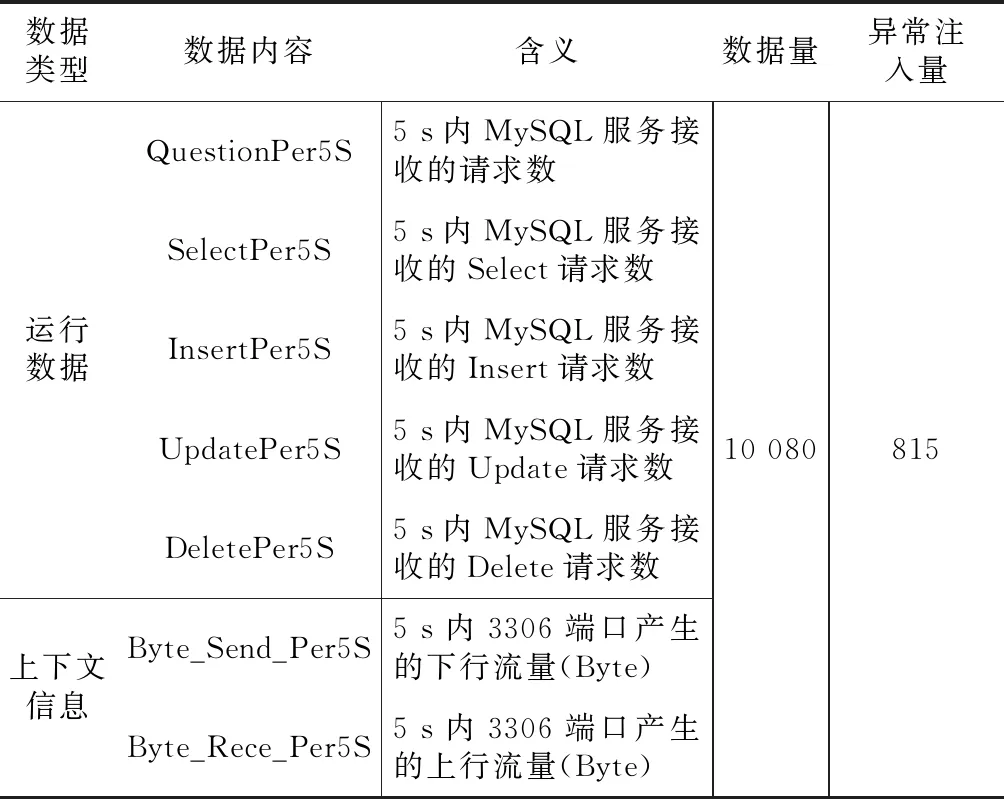
Table 1 MySQL service composition data content表1 MySQL服务组合数据内容
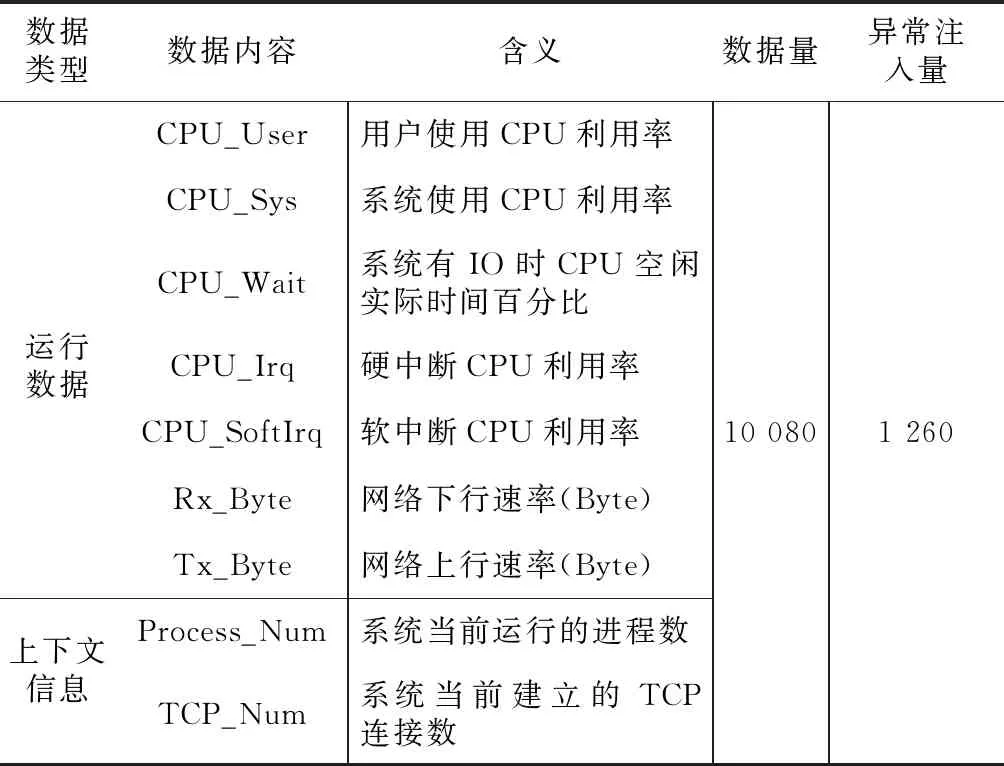
Table 2 IaaS service composition data content表2 基础设施服务组合数据内容
测试数据集的MySQL服务和基础设施服务组合数据的数据量都为10 080条,其中MySQL服务数据中包含815条注入的异常数据,基础设施服务数据包含1 260条注入的异常数据。此外,为了建立数据特征,本文分别采集了2 000条正常运行状态下的MySQL服务和基础设施服务组合数据,并按照3.2.1节中的方法分别对2种服务组合数据进行了处理。
本文分别使用文献[8]的异常检测方法(方法1)、加权LOF异常检测方法(方法2)、加权LOF结合上下文判断的异常检测方法(方法3)对MySQL服务数据和基础设施服务数据进行了对比实验。在同一环境中进行多次实验,实验中涉及到的初始化参数选取多次实验的近似最优值,如表3和表4所示。

Table 3 Initialization parameter table of MySQL service experiment 表3 MySQL服务实验初始化参数表

Table 4 Initialization parameter table of IaaS service experiment 表4 基础设施服务实验初始化参数表
使用上述方法对MySQL服务和基础设施服务进行实验,并采用真正率TPR(True Positive Rate)、真负率TNR(True Negative Rate)、正确率CDR(Correct Detection Rate)进行衡量[16],实验结果如图2和图3所示。
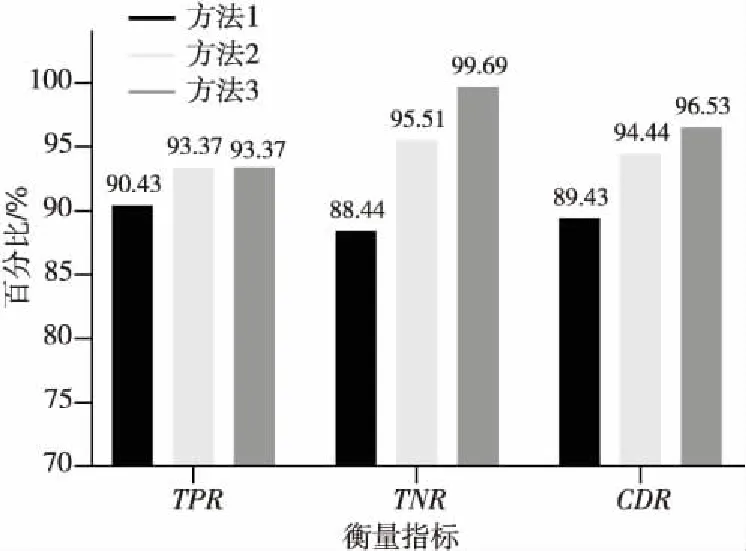
Figure 2 Experimental results of MySQL service in experiment 1图2 实验1的MySQL服务实验结果
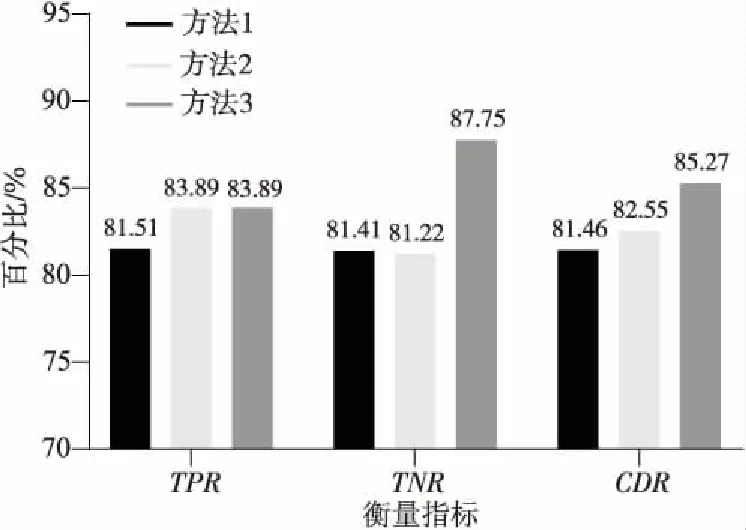
Figure 3 Experimental results of IaaS service in experiment 1图3 实验1的基础设施服务实验结果
实验结果表明,在kLOF和LOFthreshold等参数都保持相同的情况下,方法2对MySQL服务检测的真正率、真负率和正确率指标都略优于方法1的,分别有2.94%,7.07%,5.01%的提升,对基础设施服务检测的真正率和正确率也有2.38%和1.09%的提高。在对2种服务运行数据异常检测的真负率上,方法3相比方法2分别提高了4.18%和6.53%。
4.2 实验2
为了进一步验证本文方法在云环境真实应用场景中的有效性,在云环境中进行仿真实验。使用Java语言开发了“自行车租赁系统”等多个Web应用程序并将其部署在云环境中的Master节点上。使用4.1节中的原型工具采集真实应用场景中的MySQL和基础设施服务组合数据各11 120条,其中MySQL服务组合数据包含915条注入异常数据,基础设施服务组合数据包含950条注入异常数据。为了建立数据特征,分别采集了3 000条正常运行状态下的MySQL和基础设施服务组合数据建立数据特征。
各方法都采用实验1中的初始化参数,再次对MySQL服务和基础设施服务进行对比实验,实验结果如图4和图5所示。
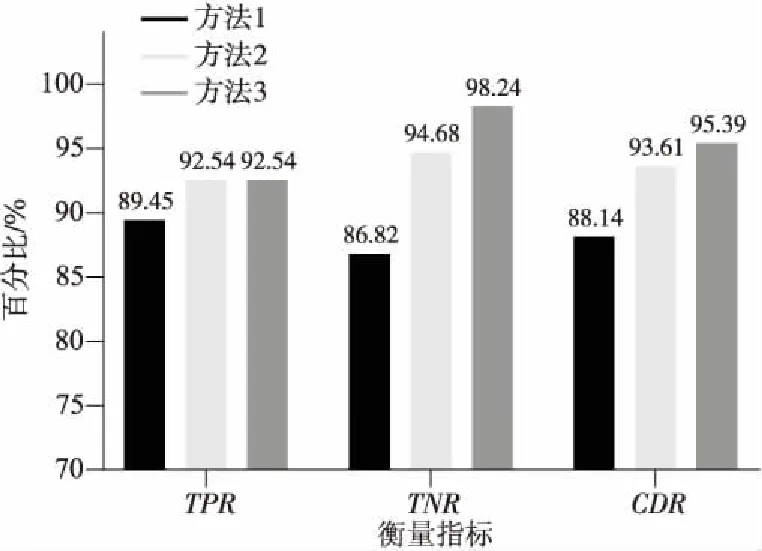
Figure 4 Experimental results of MySQL service in experiment 2图4 实验2的MySQL服务实验结果

Figure 5 Experimental results of IaaS service in experiment 2图5 实验2的基础设施服务实验结果
实验结果表明,在云环境的真实应用场景中,方法2对MySQL服务检测的真正率、真负率和正确率指标都略优于方法1的,分别有3.09%,7.86%,5.47%的提升,方法2在对基础设施服务检测的真正率和正确率方面略优于方法1,分别有2.07%和0.66%的提升。因为方法2在计算数据间的欧氏距离时考虑了服务运行数据各维度的不确定性,提高了异常检测的准确率。此外,在异常检测的真正率方面,方法3和方法2相等,原因是2种方法在初次异常判断时流程相同,不同的是前者在二次异常判断时使用了上下文信息对初步异常服务运行数据进行了二次判断,降低了误报率,从而提升了真负率。因此,使用方法3对2种服务运行数据异常检测后的真负率比方法2分别提高了3.56%和5.44%。通过2次实验表明,本文方法在云环境真实应用场景中也具有一定的可行性。
5 结束语
本文提出了一种加权LOF结合上下文判断的云环境中服务运行数据异常检测方法,首先考虑服务运行数据各维度属性存在的不确定性不同,对LOF算法进行了改进,使用加权LOF算法进行服务运行数据的初次异常判断。然后,通过处理服务组合数据建立数据特征,综合考虑上下文信息后对初步异常服务运行数据进行二次异常判断。但是,本文还存在不足,加权LOF结合上下文判断的云环境中服务运行数据异常检测方法相比加权LOF异常检测方法在2种服务运行数据异常检测的真正率方面没有提高。因为进行初次异常判断时,判断得到的正常数据集中有可能存在异常数据,而在本文方法中没有对这些正常数据集中的异常数据进行深入判断,从而将这些异常数据漏报了,下一步需要对此继续进行研究。
