面向属性网络的可重叠多向谱社区检测算法*
2020-06-22李青青马慧芳吴玉泽刘海姣
李青青,马慧芳,2,吴玉泽,刘海姣
(1.西北师范大学计算机科学与工程学院,甘肃 兰州 730070; 2.桂林电子科技大学广西可信软件重点实验室,广西 桂林 541004;3.甘肃农业大学管理学院,甘肃 兰州 730070)
1 引言
在网络分析中,社区检测是最重要和最基本的任务之一,常被认为是图聚类问题,应用于合著关系网络和细分市场识别[1]等领域。在许多应用中,网络中节点附有属性信息(如合著关系网络中作者的研究领域、发表论文篇数等信息),且节点可属于多个社区(如合著关系网络中作者致力于多个研究领域)。随着网络分析研究的深入,现已有大量有效的社区检测技术被提出。然而多数社区检测方法并没有考虑节点的附带属性等信息,并且已有可重叠的社区检测方法往往难以定位离群点。在针对属性网络的社区检测方法中,谱算法[2]是流行的社区检测算法之一,具有实现简单的优势且通常优于传统的社区检测算法。
传统谱算法主要针对结构图聚类,且节点隶属于多个社区的信息被忽略,影响社区检测的结果。近年来的谱算法对传统谱算法进行了改进,可以归纳为以下两方面:一是面向属性网络的不可重叠谱社区检测方法,其主要思想是综合考虑网络拓扑结构和节点附着的属性信息,使用归一化拉普拉斯矩阵特征向量的谱算法。其中具有代表性的不可重叠社区检测算法有,Jia等人[3]将属性的重要性与信息熵相结合来选择合适的属性,并引入属性约简方法改进谱聚类,提出了NRSR-SC(Spectral Clustering based on Neighborhood Rough Sets Reduction)算法。Bonald等人[4]考虑网络拓扑结构并结合属性信息分配给节点的权值,量化了节点间的相对重要性,这种谱嵌入是基于适当的拉普拉斯变换的第一特征向量。尽管上述算法在效率和精度方面均有提升,但是随着现实世界对网络研究的深入,发现社区之间存在的自然重叠现象不容忽视。面向属性网络的可重叠社区检测方法结合了网络拓扑结构和节点属性的相似度,综合考量将信息映射成特征值与特征向量的方式。如Goyal等人[5]使用谱聚类算法解决社区检测问题,设计了更快速的谱聚类近似算法。Li等人[6]针对网络收敛特性,提出基于节点收敛度的重叠社区检测算法SCNCD(Spectral Clustering based on Node Convergence Degree)。该算法同时考虑节点的局部和全局信息,利用改进的PageRank算法得到全局网络中各节点的重要性,并结合局部网络信息度量结构的收敛程度,通过谱聚类来识别重叠群落。尽管这类工作充分考虑了网络中的信息并可用于可重叠的社区检测任务中,但仍然无法基于谱算法检测出网络中的离群点,也无法控制重叠程度,且具有社区划分数量限制的局限性。
针对以上问题,本文从网络拓扑结构和属性两个角度出发,设计了面向属性网络的可重叠多向谱社区检测算法OMSCD(Overlapping Multiway Spectral Community Detection)。该算法可将网络划分成任意数量的社区并有效发现离群点。首先,从结构和属性两方面综合考虑,基于结合结构和属性信息的计算加权模块度设计了最大化到向量分区的节点映射方法;其次,考虑簇中心向量的初始选择对于社区检测结果的影响,给出簇中心向量的初始选择策略,并将其融合在面向属性网络的重叠度和离群度制约中,实现具有离群点的可重叠社区的发现;再次,设计节点分配策略,将节点分配给与其簇中心向量具有最高内积的社区;最后,通过节点隶属社区的情况,高效地在属性网络中检测出内部结构紧密、外部连接稀疏、可重叠和具有离群点的社区。将本文算法应用于真实网络中,实验结果表明,即使是在社区规模不平衡的情况下,本文算法也具有较好的性能,从而验证了本文算法的有效性和效率。
2 基础知识
2.1 问题定义
给定属性图G=(V,E,F),其中V={vi}i=1,…,n表示图中节点集合;E={(vi,vj)|vi,vj∈V}表示边集且|E|=m。G的拓扑结构记作邻接矩阵A,若(vi,vj)∈E,则Aij=1;否则Aij=0。F={f1,f2,…,fd}是图中属性的集合。fvi=[fvi1,fvi2,…,fvid]T是节点vi∈V的属性向量。构建加权邻接矩阵Aw,其元素定义如下:
(1)
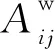
此外,为了描述清晰起见,本文涉及到的常用符号定义总结如表1所示。
2.2 加权模块度
模块度常被用来衡量社区划分质量,对于无向无权图,表示社区内的真实连边与网络在随机放置下的期望连边之间的差值。模块度越大表示社区划分质量越好。已有社区检测方法中常常利用模块度最大化思想来发现具有最高模块度取值的网络,从而捕获网络中的社区划分。在面向属性网络的社区检测中,将节点所携带的属性向量化,以其属性相似性值作为边权重,综合节点的属性和结构信息。因此,用加权模块度比用传统模块度度量社区划分质量效果更佳。

Table 1 Commonly used notations definition表1 常用符号定义
定义1(加权模块度) 给定Aw,加权模块度计算所下所示:
(2)
其中,mw是Aw中边的权重和值;cij是指示函数,如果节点vi和节点vj在同一个社区,则cij=1,否则cij=0。容易看出,加权模块度中考虑了属性权重信息。其取值越接近于1,社区结构越明显,质量越好。

Figure 1 Framework of overlapping multiway spectral community detection algorithm图1 可重叠多向谱社区检测算法框架
现实网络中存在自然重叠的现象,很多网络中存在可重叠社区。例如,在社交网络中,其中的每个节点对应于通常参与多个社区的个体。
定义2(可重叠社区) 图中节点被划为k个簇与离群点的集合C={C1,C2,…,Ck,Ck+1},其中Ci(i=1,2,…,k)表示特定社区,Ck+1是离群点集合。C1∪C2∪…∪Ck⊆C,且∃Ci∩Cj≠∅,即网络中的某些节点不仅仅隶属于单个社区,而是可同时属于多个社区。
2.3 可重叠的多向谱社区发现算法基本框架
本文提出的算法流程如图1所示,首先通过计算节点间的属性相似性将值赋给节点间的边,生成加权邻接矩阵;其次,将生成的加权邻接矩阵视为加权图,应用加权模块度来将加权模块度矩阵分解成特征值与特征向量的表示形式,从而得到节点的向量化表示,并将其融入到加权模块度中,重写加权模块度;再次,选择初始簇中心向量,并设置重叠度与离群度制约;最后,将节点划分到节点与其簇中心向量内积最大的社区,循环更新,得到使得加权模块度极大的具有离群点的可重叠社区。
3 面向属性网络的可重叠多向谱社区检测
3.1 节点映射
将节点属性间的相关性转化为节点间的边权重信息,再将加权模块度矩阵分解成特征值与特征向量的形式,得到了节点的向量化表示。根据定义1,可将加权模块度矩阵分解[7,8]成如下形式:
加权模块度矩阵为n×n的对称矩阵B,其矩阵元素定义如下:
(3)
则式(2)中的Qw可改写为:
(4)
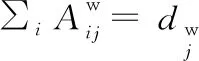
(5)
由于B的对称性,可将其改写成特征值与特征向量的分解形式:
(6)
其中,λl是B的特征值;Uil是正交矩阵U的元素,正交矩阵U的列是特征值所对应的特征向量。不失一般性,将特征值递减排序:λ1≥λ2≥…≥λn。
结合式(2)和式(6),重写Qw为:
(7)

(8)
改写式(8)如下:
(9)
根据加权模块度的特征值与特征向量的近似,即将节点向量化表示,定义一组n个p维节点向量ri[9],向量ri中各值由式(10)计算得到:
(10)
改写式(9)得:
(11)
其中,i∈s表示节点vi属于簇s。
更具体地,n个p维节点向量ri在整个优化过程中是常数(因为ri是用加权模块度矩阵的特征值与特征向量表示的)。然后,将网络划分成簇的加权模块度(除了常数1/(2mw))的贡献和,其中一个簇的贡献等于该簇中节点的向量和的平方。社区发现的目标是最大化加权模块度的划分,该问题称为最大和向量分割问题,简称向量分割问题。接下来,给出一种启发式算法来快速解决向量分割问题。
3.2 簇中心向量的选择
在面向属性的可重叠的多向谱社区检测算法中,将属性数据作为网络的辅助信息以增强网络拓扑结构间的强度。通过将考虑了网络拓扑结构和节点携带的外部属性信息融入到加权模块度公式中,得到了更精确的节点映射。通过每个节点的向量化表示,选择k个社区的簇中心,以此来开展社区检测任务。最简单的k个簇中心的选择策略是在n个节点中随机选择,但是这种策略具有较高的时间花销。因此,本节设计了一种在属性网络中的可重叠多向谱算法的簇中心节点选择策略。
考虑到在最简单的情况下,选择指向随机方向且具有相同维度的簇中心向量即可。但是,由于网络中存在社区结构,希望指向少数方向的多数节点向量被聚类,没有或者很少的向量指向其他方向。并且选择远离集群方向的初始簇中心向量是没意义的。因此,本文算法从节点向量中随机选择簇中心向量而不是选择随机方向的簇中心向量。这就保证如果大多数节点向量指向几个方向,那么选择也指向这些方向的初始簇中心向量。事实上只需要以这种方式选择k个簇中心向量中的k-1个,最终向量将由簇中心向量总和为零来决定。
均匀向量l=(1,1,1,…)始终是加权模块度矩阵的特征向量,这意味着所有其他特征向量的元素—即正交矩阵U的列必须总和为零(因为其必须正交于均匀向量)。根据式(10)有:
(12)
从而得到:
(13)
和
(14)
因此,一旦随机选择了k-1簇中心向量,第k个就可以利用式(14)计算。由于在初始化过程中存在一个随机元素,所以在参数取值相同的相同网络中,结果也不一定相同。因此,需在不同的初始条件下多次运行算法,选择最高加权模块度的社区划分。
3.3 属性网络的重叠度和离群度制约
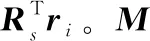
给定参数α与β,对于M使用参数α与β进行约束[11]:
(15)
3.4 可重叠的多向谱社区检测
类似于k-means算法,OMSCD算法用向量代替点,向量内积代替距离。首先,选择簇中心向量矩阵R中的一个簇Cs,将节点向量ri分配给与其距离最近的簇中心向量所在的簇,然后根据这些分配为每个簇计算新的簇中心向量并重复,新的簇中心向量为每个簇中节点向量的和,即:
(16)
可将式(11)改写以最大化式(17)的目标函数:
(17)
当Qw与在上一轮计算的Qw相比值有所下降时,则认为上一轮使得Qw值极大的值为最好的划分结果,即Qw达到收敛。社区检测结果观察加权模块度的特性。假设将节点vi从一个社区Cs移动到另一个社区Ct,设Rs和Rt表示不包括节点vi的贡献的2个社区的簇中心向量。然后,在移动之前,社区的簇中心向量是Rs+ri和Rt,移动后是Rs和Rt+ri。所有其他社区在此期间保持不变。因此,在移动节点vi时加权模块度的变化△Qw是:
(18)
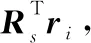
算法1OMSCD算法
Input:G=(V,E,F),社区数k,重叠度参数α,离群度参数β。
Output:指示矩阵M。
1:利用式(1)计算Aw;
2:利用式(3)计算B;
3:利用式(6)分解矩阵B,得到B的特征值与特征向量;
4:fori=1ton
5: 利用式(10)计算ri;
6:endfor
7:初始化簇中心矩阵R;
8:初始化指示矩阵M全为0;
9:while目标函数没有收敛do
10:fori=1ton
11:forj=1tok
13:endfor
14:endfor
15: 初始化T=∅,S=∅,p=0;
16:whilep<(n+αn)do
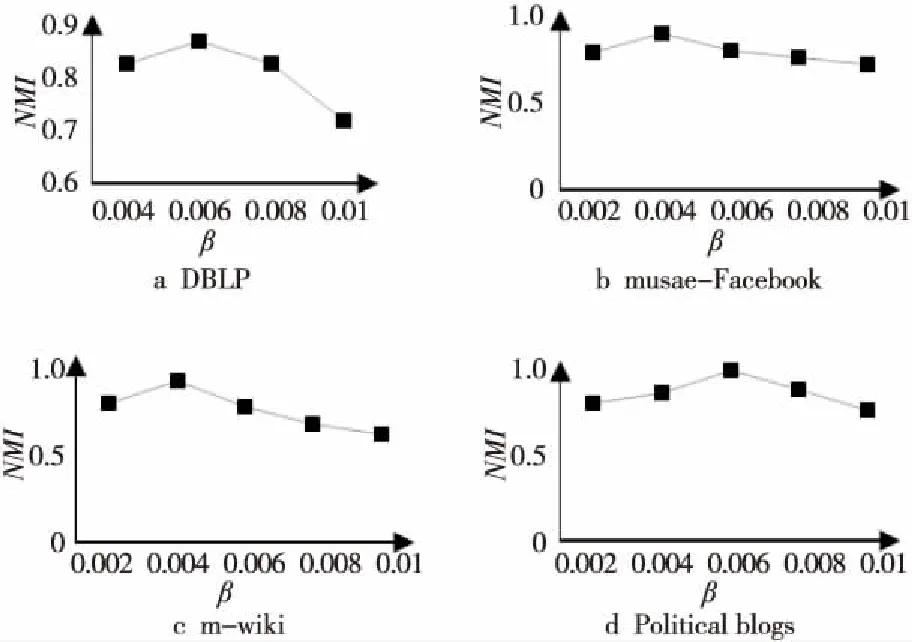
17:ifp 19:S=S∪{vi*}; 20:else 22:endif 23:T=T∪{(vi*,Cl*)}; 24:p=p+1; 25:endwhile 26: 根据式(16)更新簇中心矩阵R; 27: 计算节点向量ri与簇中心向量Rs的内积,更新矩阵O; 28: 根据式(17)计算目标函数; 29:endwhile 在算法1中,第1~3行根据公式计算Aw、B、B的特征值与特征向量;第4~6行得到节点的向量化表示;第7行依据3.2节初始化簇中心向量;第9~29行将图中的每个节点分配到相应的社区中。第15行中T是存放节点vi属于簇Cl的集合,集合中的元素为节点和相应簇的二元组;S存放被分配了的节点的集合;第17~20行用来判断重叠度是否达到要求,若达到,将节点进行分配,否则停止分配;第26行更新簇中心向量;第28行计算目标函数,得到最好的社区检测结果。 时间复杂度分析:在算法1第3,4行计算节点向量时,时间复杂度为O(n);将网络划分成k个可重叠的簇,计算节点向量ri与簇中心向量Rs的乘积oij,复杂度为O(nk);再根据oij对节点进行划分时,时间复杂度为O((n+αn)×nk),由于α经常取较小的值,故时间复杂度为O(n2k);给定指示矩阵,更新簇中心矩阵的时间复杂度为O(nk);给定簇中心矩阵R,只需遍历整个网络一次来更新矩阵O,因此时间复杂度为O(nk)。设t为目标函数收敛所需时间,整个算法的时间复杂度为O(n+tn2k)。 为了验证本文算法的有效性和效率,设计实验进行验证,实验将回答以下几个问题: 问题1OMSCD算法与现有在属性网络中的谱方法相比,性能方面存在哪些优势? 问题2针对在面向属性网络的具有离群点的可重叠多向谱社区检测任务,不同参数的设置是怎样影响本文算法的? 问题3在真实的网络中,实现社区检测任务的效果如何? 4.1.1 人工数据集 使用LFR基准[12]生成允许节点隶属于多个社区的属性网络。具体地,节点的度和社区规模大小分布分别由指数T1和T2控制。给定社区所需的节点数,通过分区约束将邻接矩阵分成块,为每一个块选择概率Pij,以衡量每个区块之间的密度。对角线上的块为实际社区,非对角线块为社区间的交叉边。另外,为节点分配属性fi∈[0,1],属性值需从正态分布N(μ,σ)中提取,其余的属性从具有更大方差的正态分布N(0,1)中提取[13]。此外,为了检测离群点与重叠社区,使该人工数据集至多具有βn个离群点,重叠度α的设置满足0≤α≤(k-1)且α≼(k-1)。其他参数设定为T1=2,T2=1,Pij=0.36,i≠j。表2给出了人工数据集的具体信息。 Table 2 Synthetic datasets表2 人工数据集 4.1.2 真实数据集 选取如表3所示的4个真实世界中可重叠的属性网络进行验证。第1个数据集是DBLP(Digital Bibliography Library Project)的作者合著关系网络。在该网络中,节点表示作者,以作者间的合著关系为边构建关系网络,边权重表示作者间的合作次数。musae-Facebook数据集是Facebook站点的页面-页面图。节点代表官方的Facebook页面,边表示站点之间的相互喜欢,节点特征从站点描述中提取而来。第3个数据m-wiki来源于英文维基百科,代表特定主题的页面-页面网络,其中节点表示文章,边表示文章之间的相互链接。第4个数据集是美国Political blogs之间的定向超链接网络,将节点间的有向边视为无向边验证本文的算法。其节点表示博客,边表示博客间的链接,政治倾向为属性。真实数据集的具体信息由表3所示。 Table 3 Real datasets表3 真实数据集 社区检测任务常使用F-score和NMI作为评价指标[14,15],定义如下: 定义2(F-score)F-score是召回率和精确率的调和平均: (19) 其中,Precision=|CT∩CF|/|CF|,Recall=|CT∩CF|/|CT|,CT表示真实社区,CF表示检测到的社区。F-score值越大算法性能越好。 定义3(归一化互信息NMI)NMI基于混淆矩阵N定义如下: (20) 其中,Nij表示属于真实社区Ci和检测到的社区Cj的节点的数量,Ni.是矩阵N中第i行中的元素构成的行向量,N.j对应于矩阵N中第j列元素构成的列向量。NMI度量了算法检测结果与真实结果的相似性,相似性越高,NMI值越接近于1。 4.3.1 性能比较(问题1) 选取了NRSR-SC[3]、SCNCD[6]与本文算法分别从社区检测的准确性和运行时间两方面进行比较。其中NRSR-SC算法创新地提出采用约简属性来改进谱聚类进行不可重叠的社区检测;SCNCD算法同时考虑节点的局部和全局信息通过谱聚类来识别重叠社区。因此,本文选取上述2种算法作为实验参照。 表4显示了在不同数据集上NRSR-SC、SCNCD算法与OMSCD算法结果的F-score和NMI的值。从表4中可以看到,NRSR-SC算法在较小的数据集上相比其他算法的性能较低,如Political blogs。这是由于属性约简方法降低了部分性能。SCNCD算法同时考虑了局部和全局的信息使其在较小的数据集上表现出了良好的性能,然而较多考虑局部信息使其在较大数据集上的性能有所降低。不论NRSR-SC算法还是SCNCD算法都对数据集的规模比较敏感,算法的F-score和NMI值受到了数据集规模的影响。而OMSCD算法由于选择了与大多节点方向类似的簇中心向量,同时可检测出重叠社区和离群点,不仅在不同规模的数据集上的性能表现较好,而且也具有较好的精度。 Figure 2 Comparison of algorithms runtime on different datasets图2 不同数据集上算法运行时间对比 图2给出了在4个真实数据集和3个人工数据集上的运行时间对比结果。随着数据集规模的不同,3种算法的运行时间有所变化。其中OMSCD算法在各个数据集上都表现出了良好的性能,其运行时间是所有算法中最短的,比其他算法快6 s左右。一方面,这是源于本文算法节点映射时近似求解了对加权模块度贡献最大的特征值特征向量。另一方面,这是由于OMSCD算法簇中心向量的初始选择,使其效率高于其他算法的。NRSR-SC算法和SCNCD算法的运行时间之所以长于本文算法的,是源于NRSR-SC算法属性约简过程占用了较多的时间,而SCNCD算法则是由于利用了节点收敛度等方法,使其在较大规模数据集上花费了较长时间。 4.3.2 参数研究(问题2) 分析OMSCD算法2个重要参数α与β,讨论如何选择α与β。现实中,一些聚类算法的模型参数设置不直观,或者难以预测特定的参数设置的结果,但是OMSCD算法中的参数是直观的,允许用户自己设置。因此,用户可以从自身的领域出发决定参数的设置。接下来将给出参数α与β对于本文算法的影响分析来估计参数α与β的设置。 Table 4 Comparison with other algorithms表4 与其他算法的比较 Figure 3 Influence of α on OMSCD algorithm on different datasets图3 不同数据集上α对于OMSCD算法的影响 从图4中可观察到,随着β值的增大,OMSCD算法的NMI值在逐渐下降。主要原因是较大的β会将原本隶属于社区内的节点视为离群点进行处理,从而对社区检测结果产生影响。在本文中,离群度参数β的设置是非穷举的。接下来将给出运行本文算法进行社区检测时离群度参数β的设置建议。在运行本文算法时,设zi表示节点vi与最接近的簇中心之间的距离。计算zi(i=1,…,n)的平均值(用μ表示)和标准差(用σ表示)。如果距离zi大于μ+3σ,则认为节点vi为异常点。也就是说,如果通过遵循统计中的3σ规则,节点到其最接近聚类的距离大于均值的3个标准差,则认为节点是异常点。这样,就可以估计离群点的数值,从而得到β值。 Figure 4 Influence of β on OMSCD algorithm on different datasets图4 不同数据集上β上对于OMSCD算法的影响 在本节中,设计一个案例分析来观察所提出的OMSCD算法的性质。研究节点上所附着的属性对于节点向量表示的作用,解释4.3.1节所提到的簇中心向量的选择对于社区检测结果的影响以及是否可准确地检测出离群点和可重叠社区,并观测OMSCD算法的实用性。该案例将在美国的Political blogs网络上进行,Political blogs网络相对较小,可以直观地显示OMSCD算法的结果。 实验结果如图5所示,其中重叠度参数α=1,离群度参数β=0.007。利用OMSCD算法进行社区检测任务。 Figure 5 Community detection results of OMSCD algorithm on the American Political blogs network图5 OMSCD算法对美国Political blogs 网络的社区检测结果 从图5可以看出,OMSCD算法将其分成了2个簇,矩形框中的节点、虚线椭圆区域中的节点分别表示政治倾向为正派和反派的信息。网络中的重叠社区为实线椭圆框圈中区域,表示政治倾向为中立派。未圈中的节点是离群点,表示不参与任何派系。结果显示,在属性网络Political blogs中,采用融合属性信息和网络拓扑结构的加权模块度,通过加权模块度最大化得到的节点向量有效地提高了社区检测精度,并进一步证明了簇中心向量的初始选择策略有助于提高算法的效率。此外,利用重叠度和离群度制约检测出了可重叠社区以及网络中存在的离群点。 本文针对现有谱算法受限于划分数量且难以控制重叠程度的局限性,提出了面向属性网络的具有离群点的可重叠多向谱社区检测算法。首先通过计算节点间的属性相似性将值赋给节点间的边,生成加权邻接矩阵。同时,将属性信息融入到加权模块度中,利用考虑属性信息的加权模块度将节点映射到向量空间,通过设置重叠度和离群度,实现可重叠的多向谱社区检测。在真实数据集上的实验表明,本文算法在社区检测任务中优于传统的谱算法。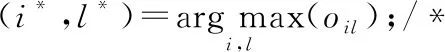
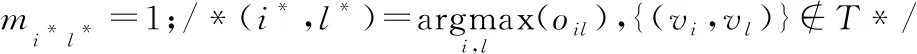
4 实验与结果分析
4.1 实验数据集描述


4.2 评价指标
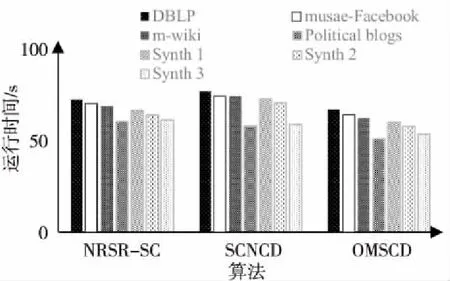
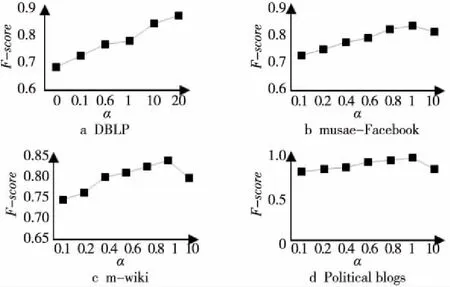
4.3 实验结果与分析


4.4 案例分析(问题3)

5 结束语
