陶瓷/芳纶纤维复合靶板防弹性能研究及结构改进

王亚进 王 陶* 王良模 沙小伟 黄 健 陈 威

(1.南京理工大学 机械工程学院， 南京 210094； 2.苏州江南航天机电工业有限公司， 苏州 215300)

引 言

现代战争中，防弹装甲材料是军事力量的核心技术之一。而随着科学技术的发展，对防护装甲的要求越来越高，因此，研发轻质、高强度、具有良好防弹性能的新型材料迫在眉睫。

目前已有一些针对防弹新型材料展开的研究工作。安振涛等[1]设计了一种阵列式陶瓷颗粒破片防护层的新型防弹材料，并利用仿真分析的方法验证了该材料具备良好的防弹性能，研究结果可以为阵列式陶瓷颗粒破片防护层的优化设计提供参考。高华等[2]利用数值模拟的方法分析了纺织复合材料和陶瓷的低速冲击性能，剖析了陶瓷/复合材料装甲板受弹头冲击时的防弹机理，为复合材料在复合装甲上的应用及其防弹能力预测提供了理论分析的依据。Hu等[3]研究了碳化硅陶瓷层单元结构的差异对于靶板防弹性能的影响，提出了陶瓷钢板的结构，分析了圆柱形、六角形以及长方形单元结构阻碍子弹侵彻过程的差异，为复合靶板设计中碳化硅单元结构的选择提供了理论参考。

目前广泛用于防弹的三大陶瓷材料是氧化铝、碳化硅和碳化硼，相比于金属防弹板而言，陶瓷的特点是密度小、硬度高和模量高。考虑到氧化铝和碳化硅的密度指标、力学特性和防弹性能都比较优越，而对于密度较小且防弹性能优越的碳化硼陶瓷，由于加工技术的限制，不适合大规模使用[4]。而纤维作为装甲材料，能够大幅度地减小装甲的质量，并且由于其断裂安全性好、可设计性强、具有良好的制作工艺性，因此被广泛地应用于各种防弹装甲上[5]。

目前，很多学者都对陶瓷和复合材料的失效机理、制备工艺及影响因素进行了研究[6]，也有针对陶瓷和复合材料构成的复合靶板的防弹性能的研究工作[7]，但很少有关于如何通过优化靶板结构来提高其防弹性能的研究。本文在课题组前期与苏州某公司合作项目成果的基础上，基于芳纶纤维和陶瓷良好的防弹性能，提出了一种由芳纶纤维与陶瓷复合材料构成的防弹结构，结合试验设计并利用NSGA- II算法优化了该结构，最后通过仿真模拟验证了优化结果的可靠性。

1 陶瓷/芳纶纤维子弹侵彻靶板有限元模型的建立

1.1 陶瓷/芳纶纤维材料

陶瓷选用碳化硅(SiC)和氧化铝(Al2O3)陶瓷材料作为研究对象，纤维材料选用大分子链高度取向结晶的芳纶纤维。

1.2 几何模型

防弹标准参考警用防暴车的B级防护标准，其使用的子弹为56式7.62 mm普通弹，子弹由外到内分别是覆铜披甲、铅芯及钢芯，子弹长度为32.3 mm，质量约为8.096 g。防弹靶板分别为6 mm厚的碳化硅和15 mm厚的芳纶纤维，横向尺寸为45 mm×45 mm。对子弹和靶板分别建立几何模型，如图1(a)所示。

1.3 有限元模型的建立

1.3.1单元选择和网格划分

将建立好的几何模型导入Hypermesh软件中进行网格划分，选用Lagrangian算法，采用4节点四面体单元和8节点六面体单元划分网格。需要说明的是，由于子弹垂直作用在靶板上，为了减少计算时间，有限元模型采用1/4的几何模型，如图1(b)所示。

1.3.2材料参数

为了更好地描述子弹的模型，选择Johnson_Cook材料模型与Gruneisen状态方程相结合的方式，其中Johnson_Cook本构模型关系为

(1)

陶瓷等脆性材料的材料模型采用由Johnson和Holmquist提出的JH- 2模型，该模型中未损伤陶瓷和已损伤陶瓷的强度由一组随压力、应变率和损伤演化的经验关系确定[9]。模型中未损伤陶瓷的强度为

(2)

损伤陶瓷强度为

(3)

芳纶纤维是由多个单层的纤维材料经过粘接形成的层压板结构，材料模型选择的是composite_failure模型，该模型可以准确地描述纤维复合材料在受冲击时的响应过程[11]。

本文仿真选用的SiC和Al2O3陶瓷的材料性能参数是由项目前期进行的相关试验得到的，如表1所示。表中，ρ为材料密度；G为剪切模量；EPSI为准静态阈值应变率；T为最大拉伸压力强度；SFMAX为最大归一化断裂强度；HEL为Hugoniot弹性极限；PHEL为Hugoniot弹性极限处的压力分量；β为弹性势能损失转化为静水能的比例。

芳纶的材料性能参数同样也是由试验得到，如表2所示。表中，EA为纵向弹性模量；EB为横向弹性模量；EC为法向弹性模量；PRBA为法向泊松比量；PRCA为横向泊松比；PRCB为纵向泊松比；GAB为纵向剪切模量；GBC为法向剪切模量；GCA为横向剪切模量。

表1 不同陶瓷JH- 2模型参数

表2 芳纶材料模型参数

1.3.3边界条件设置

由于有限元模型采用的是1/4模型，因此对靶板的对称面定义对称约束，而靶板边缘则采用固定约束方式。

子弹和靶板之间采用单面侵蚀接触CONTACT_ERODING_SINGLE_SURFACE。此类单面接触的算法对于处理接触区域不能提前预知的自接触或者大变形问题是非常有效的，并且所有的外表面都在搜索范围内，因此不需要定义接触面与目标面。侵蚀接触用于保证删除外部的失效单元后，剩下内部的单元还可以保持接触[12]。

2 陶瓷及芳纶纤维防弹性能分析

对子弹侵彻靶板的模型进行前处理并检查无误后提交LS- DYNA计算，对仿真结果进行分析。

2.1 陶瓷和纤维破碎形态分析

SiC陶瓷和芳纶纤维受到子弹冲击后的破碎形态如图2所示，可以看到，在子弹的冲击作用下陶瓷产生的碎块比纤维的大很多，在子弹侵彻过后，陶瓷靶板上形成的弹孔形状较大，弹孔内部的形状比较粗糙，在靶板的表面处尤其是背面又因冲击产生了特别明显的陶瓷锥飞溅。而纤维主要发生的是剪切破坏，整体的变形较小，内部的形状比较平滑，子弹穿透纤维板材后，没有明显的分层和脱层现象，整个靶板仍然是一个整体。

2.2 陶瓷抗侵彻性能分析

从图3(a)中可以看到，在侵彻陶瓷靶板时子弹的速度衰减过程非常明显，尤其是B至C段，该阶段对应着子弹与陶瓷靶板接触的25 μs，子弹的速度从700 m/s降至92 m/s，说明陶瓷靶板会极大地影响子弹对靶板的冲击作用，从而降低子弹的速度。从陶瓷的破碎形式(图2(a))可以看出，陶瓷吸收能量以粉碎和断裂为主，子弹在侵彻的过程中将动能转化为陶瓷的粉碎能。结合陶瓷材料的动态力学性能，根据陶瓷面板的破损情况，将陶瓷的吸能机制分为粉碎吸能和应力波吸能。

由于陶瓷本身的硬度和抗压强度都高于子弹材料的属性，因此在侵彻过程中陶瓷可以通过侵彻、钝化、破碎弹体的材料以及自身的破碎等方式来吸收弹体的动能，这个过程中弹体和陶瓷破碎所消耗的弹体动能称为冲击粉碎能。弹体和靶板的粉碎耗能除了包含冲击粉碎能还有摩擦粉碎能。当弹体与靶板接触形成粉碎区域后，接触区的陶瓷由于受到周围陶瓷的挤压及束缚作用，导致弹体和陶瓷之间存在巨大的摩擦力，致使陶瓷在接下来的侵彻过程中继续破碎，产生摩擦粉碎能，造成粉碎断裂耗能、摩擦热耗能、体积膨胀耗能等多种形式的混合耗能机制，即为摩擦粉碎能。

当陶瓷靶板受到子弹侵彻时，接触面的压力迅速增长，并迅速向靶板背部的四周传播压缩应力波，当应力波大于陶瓷材料的断裂应力时，接触界面周围的陶瓷材料将碎裂，产生陶瓷碎片。陶瓷碎片在冲击波的作用下，进行横向和反冲击方向的流动，这些碎片和粉末对子弹进一步的侵蚀，减缓并阻止子弹的侵彻过程。

2.3 纤维抗侵彻性能分析

对于芳纶纤维靶板而言，从图3(b)中可以看出，子弹的剩余速度仍然比较大，侵彻过程主要发生在B至C段，这段时间对应着子弹与芳纶纤维靶板的接触阶段。从图中可以看出，15～86 μs时间段内子弹的速度从724 m/s降至682 m/s，速度曲线的下降趋势较为平缓。由此可知，这个阶段子弹的加速度比较小，这一现象是因为芳纶纤维是由许多层纤维通过树脂胶粘而成，并且其材料属性也决定了其无法有效抵御子弹的冲击。

当子弹侵彻纤维面板时，纤维因为高速冲击发生拉伸变形，并以此形式减缓子弹的侵彻作用，当弹体进一步侵彻导致纤维的变形量超过其断裂延伸率时，纤维开始断裂。在整个过程中，子弹的动能先转化为纤维的弹性势能，最后转化为纤维的断裂能。

3 陶瓷/芳纶纤维复合靶板优化设计

基于第2节的研究结果，提出采用高强度纤维和陶瓷共同构成复合材料靶板，与传统的金属材料制成的防弹靶板相比，这是一种更为有效的轻型防护装甲。陶瓷的硬度虽然很高，但是它的塑性较差、断裂强度低，而纤维的模量很高，具有非常高的韧性，有足够的刚度作为背板支撑陶瓷材料，以陶瓷作为防弹面板、纤维作为防弹背板的结构能充分发挥两种结构的优势，可以提升靶板的防弹性能。

将3 mm厚的SiC陶瓷、5 mm厚的Al2O3与15 mm厚的芳纶纤维组合构成防弹复合靶板，如图4所示。

靶板的面密度为44.62 kg/m2，当子弹以725 m/s的速度侵彻靶板时，剩余速度为131 m/s，侵彻深度等于靶板厚度，为23 mm。从防弹性能角度出发，这样的结构显然是不能满足要求的，因此需要对复合靶板的结构进行优化。

对复合靶板结构进行优化，首先要考虑的是子弹侵彻靶板后的剩余速度，其次是靶板的质量，最后是子弹对靶板的侵彻深度。而复合靶板的厚度越大，子弹侵彻靶板后的剩余速度越小，靶板的质量越大，子弹对靶板的侵彻深度越小，即靶板的厚度对以上指标的作用效果不一致，因此考虑采用NSGA- II算法进行优化[13]。

3.1 数学模型

3.1.1设计变量

设计变量为SiC陶瓷层、Al2O3陶瓷层和芳纶纤维层的厚度T1、T2、T3。

确定了设计变量后，利用DOE设计方法中的最优拉丁超立方设计确定20组样本点，最优拉丁超立方设计可按照式(4)进行采样。

(4)

式中，1≤i≤k，1≤j≤k，i为第i次试验，j为第j个变量，k为样本点数量；U是0到1之间的随机数，π是0，1，…，k-1的独立随机排列，共有k!种排列。部分样本点如表3所示。

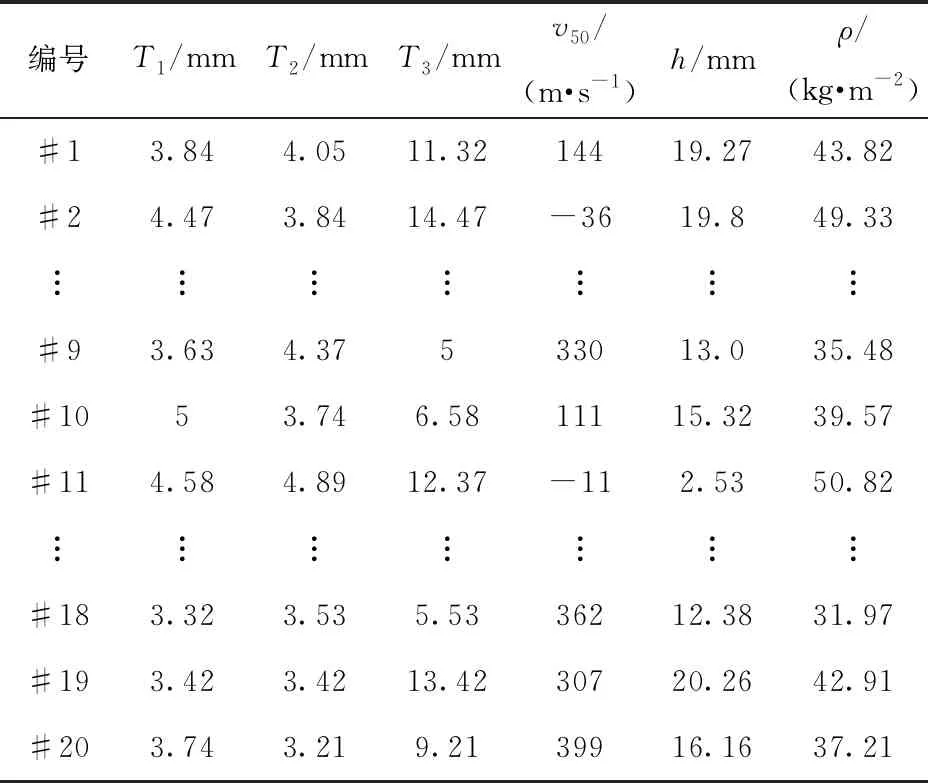
表3 最优拉丁超立方设计确定的样本点

3.1.2优化模型

在确定了优化目标及设计变量之后，可以建立多目标优化数学模型为

minf=w1v50+w2h+w3ρS

s.t.T1∈[3 mm,5 mm]

T2∈[3 mm,5 mm]

T3∈[5 mm,15 mm]

(5)

式中，v50为子弹侵彻靶板后的剩余速度，m/s；h为子弹对靶板的侵彻深度，mm；ρS为靶板的面密度，kg/m2；w1、w2和w3为权重系数，由于最优解的选择原则是以子弹的残余速度为主要选择标准，在满足条件的情况下，寻找质量最轻的最优解，即目标函数中子弹残余速度最小的情况下要求靶板的面密度尽可能小，因此w1、w2和w3取值为0.6、0.1、0.3。

3.2 计算结果分析

3.2.1建立响应面模型

利用20组样本点，运用最小二乘原理建立三阶响应表面模型，即有关v50、h及ρS的三阶多项式。通过样本点得到目标变量的响应面模型后，需要对响应面的可靠性进行验证。可以通过方差分析中的决定系数R2和调整的决定系数来对响应面的可靠性进行验证。R2的值越接近1，证明响应面的拟合效果越好。在本次20组样本点中，所建响应面模型的决定系数R2分别为0.932、0.912、0.995，调整的决定系数为0.911、0.878和0.967。由此可知，该模型对目标函数达到了高度拟合，使用此模型进行优化分析是可行的。

3.2.2优化结果分析

依据拟合出的高精度多项式响应面代理模型进行优化设计，选用NSGA- II算法进行优化计算，设置初始的种群个体数为12，进化繁殖100代，其他使用默认值，参考相应的约束函数对设计变量的取值范围进行约束，同时满足相应的目标函数，得出Pareto最优解：SiC厚度为4.54 mm，Al2O3厚度为4.50 mm，芳纶纤维厚度为7.17 mm。根据最优解建立相应的模型进行仿真计算，并与近似模型响应值对比(表4)，可以看出剩余速度和侵彻深度与近似模型结果相对误差为-3.5%和-2.6%，证明了响应面代理模型的准确性。

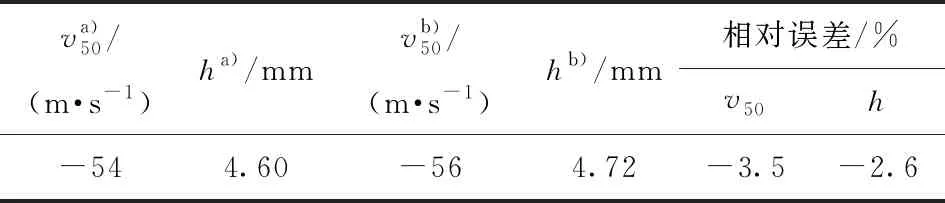
表4 最优点仿真值与近似模型响应值对比

a—模型仿真值；b—近似模型值。

表5是靶板结构优化前后的对比结果，可以看到，优化后的复合靶板在子弹侵彻后的剩余速度为-54 m/s，侵彻深度为4.60 mm，面密度为39.22 kg/m2。与优化之前相比，子弹的剩余速度降低了185 m/s，面密度降低了5.4 kg/m2，侵彻深度降低了18.4 mm。图5是复合靶板优化前后子弹的速度- 时间曲线图，B～C1段和B～C2段对应着子弹侵彻两种靶板中陶瓷的过程，通过对比可以看出，子弹侵彻两种靶板的陶瓷层所消耗的时间几乎没有变化，而子弹侵彻原始靶板时加速度的绝对值为1.825×107m/s2，小于侵彻优化之后的靶板的加速度(2.95×107m/s2)；C1～D1和C2～D2对应着子弹侵彻两种靶板中芳纶纤维的过程，可以看到，优化之后，侵彻芳纶纤维消耗的时间减少了，而侵彻过程中的加速度也由1.875×106m/s2提升至2.5×106m/s2。综合而言，可以得出，复合靶板的综合防弹性能得到了明显提高。

表5 优化前后结果对比

4 结论

(1)陶瓷和纤维在高速子弹冲击作用下的破碎形态不同，具体表现为：陶瓷受到冲击后形成的弹孔面积大于纤维的弹孔面积；陶瓷受到冲击后内部的形状比较粗糙，而纤维的内部则比较平滑。

(2)陶瓷和纤维在高速子弹冲击作用下的失效形式和吸能方式不同，具体表现为：陶瓷在弹丸冲击下的吸能主要通过自身的破碎和断裂及应力波的传递实现，将子弹的动能转化为自身的破碎能；而纤维主要通过自身的拉伸和延展将弹丸的动能转化为自身的弹性势能和断裂能。

(3)利用最优拉丁超立方的试验设计方法建立侵彻模型的三阶响应面模型，并利用NSGA- II算法对响应面模型进行优化，得出的最优解为：SiC的厚度4.54 mm，Al2O3的厚度4.50 mm，芳纶纤维的厚度7.17 mm。建立了相应的仿真模型进行验证，误差为-3.5%和-2.6%。优化后的复合靶板在子弹侵彻后的剩余速度为-54 m/s，侵彻深度为4.60 mm，面密度为39.22 kg/m2。与优化之前相比，剩余速度降低了185 m/s，面密度降低了5.4 kg/m2，表明靶板的综合防弹性能得到了明显提高。