改进小波阈值算法的去噪研究*
2020-06-21
(太原理工大学 电气与动力工程学院,山西 太原 030024)
1 引言
目前,针对非平稳信号的去噪方法主要有分离谱法、随机共振法和小波去噪法等。研究最多且应用最广泛的是小波阈值去噪方法[1],去噪效果优劣对小波基的选取有很强的依赖,缺乏自适应性,而且最佳小波分解层数难以确定,所以很难达到最优的分解效果。EMD 在信号去噪中,能自适应地选取信号内在的特征模态函数,解决了小波变换中选取最优小波基的困扰[2]。EMD 分解比小波分解更清晰、准确,去噪效果也更好,分解出的IMF 能够充分保留信号的非线性和非平稳特征[3]。EMD 在信号分解过程中易发生模态混叠[4],为解决这个问题,可通过向信号中添加白噪声,构造聚合经验模态分解,并取得了较好的降噪效果。
为了保留信号有用信息,本文提出基于EEMD 的改进小波阈值函数去噪方法,分析表明其能够更有效地去除信号中的噪声。
2 EEMD 的阈值去噪
2.1 聚合经验模态分解
对于非平稳信号,可通过EEMD 方法分解成若干特征模态分量(IMF)和残差r。其分解步骤如下[5]。
第一步,向信号x(t)中加入高斯白噪声ni(t):

式(1)中:xi(t)为第i次加入白噪声后构造的新信号。
第二步,通过EMD 对xi(t)分解,得到由高频到低频分布的n阶IMF 分量cij(t)和余项ri(t):
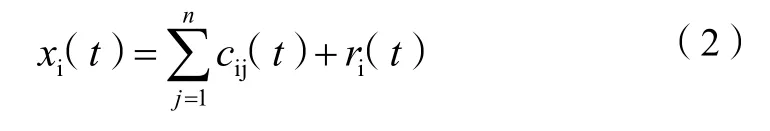
式(2)中:cij(t)为IMF 分量;ri(t)为余项。
第三步,每次加入不同的白噪声序列,上述步骤重复进行N次,将分解所求取的各阶IMF 分量的均值作为最终结果:
式(3)中:ci(t)为分解的第i个IMF 分量;N为添加高斯白噪声的数目。
2.2 基于EEMD 的改进小波阈值函数去噪
含噪信号经EEMD 分解后得到的各阶IMF 分量同时含有真实信号和噪声信息,出现噪声与信号混叠现象[6]。信号分解后得到了N阶IMF 分量,对每阶IMF 分量选取合适阈值进行处理,然后再进行信号的重构,进而完成对带噪信号的去噪。
小波阈值去噪的基本过程是:首先将含噪信号进行多尺度小波分解,然后对所得的小波系数进行阈值处理,进而应用小波逆变换重构信号,从而完成对信号的去噪。
常用的硬阈值、软阈值的阈值函数所存在的问题是:硬阈值函数处理后在λ处不连续,信号重构后可能会存在振荡;软阈值函数处理后虽然整体连续性较好,但当∣ci∣>λ时,与ci始终存在恒定偏差,影响着重构信号逼近于真实信号的程度,有着难以消除的误差。
文献[7]中提出了一种改进的小波阈值函数为:

式(4)中:0<α<1,m∈R+;λ为阈值大小。
当α→0,m→∞,该函数等效于硬阈值去噪;当时α→1,m→∞,该函数等效于软阈值去噪。对于此改进阈值函数,有两个调整参数分别为α和m,通过利用粒子群寻优(PSO)算法对参数α和m进行优化,从而寻找最优函数参数值。将输出信噪比(SNR)作为适应度函数。
2.3 基于PSO 算法优化阈值函数的调整参数值
粒子群算法首先初始化一群随机粒子,该粒子特征由位置、速度和适应度值表示,适应度值通过适应度函数求解。在每次迭代运算过程中,粒子通过个体极值和全局极值更新调整自身的速度和位置,公式如下:
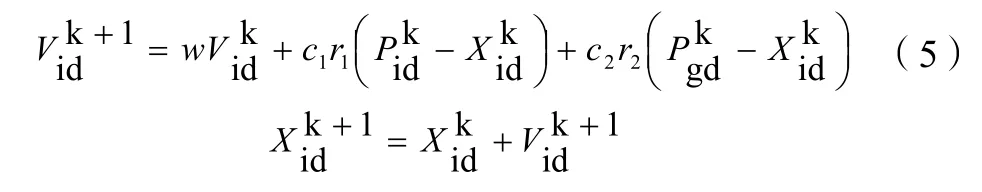
式(5)中:w为惯性权重;d为D维解空间;k为当前迭代次数;Vid为粒子的速度;c1和c2为加速度因子;r1和r2为分布于[0,1]之间的随机数。
具体实现算法去噪步骤如下:①对带噪信号进行4 层小波变换,分别将分解所得的小波系数作为粒子群寻优输入数;②参数初始化,c1=2.0,c2=2.0,粒子数N=50,迭代次数设为100,wstart=0.8,wend=0.6;③利用文献[7]中的阈值函数处理分解后的小波系数,求得估计小波系数,并计算第一次迭代中所有粒子的适应度值,确定个体、群体的最佳适应度值,分别用gbest和zbest表示;④及时对粒子个体中最优值gbest和群体最优值zbest进行更新调整;⑤如果迭代过程进行到了设定次数,则结束更新,否则继续跳转到步骤④执行命令;⑥输出得到的最优解值zbest;⑦进而求得最优调整参数值,并将其代入阈值函数中与改进的阈值相结合对带噪信号进行去噪。
对于阈值的选择,通常选用同一阈值对不同频率段的信号进行处理,去噪效果存在较大偏差,因此本文采用文献[8]的改进阈值公式,其能够随着分解层数增加,阈值取值降低,符合噪声随小波变换的变化规律,并且自适应地调整阈值大小。
3 仿真与实验
应用MATLAB 软件,对Bumps 信号、HeaviSine 信号进行实验分析,并将本文方法应用到含有噪声的多模式超声兰姆波信号中,超声回波信号采用高斯回波模型[9],模拟频率为5 MHz,采样频率为200 MHz,采样点数1 200,信噪比为10 dB 的信号模型。由于对含噪信号的去噪处理过程相似,只是处理对象不同,因此本文将着重阐述对含有噪声的多模式超声兰姆波信号进行去噪。将带噪信号经过EEMD分解后,将方差贡献率低于1%的IMF 分量去除,再对真实IMF 分量进行小波阈值去噪,然后对去噪后的IMF 分量进行重构。通过对比硬阈值、软阈值和改进小波阈值函数的去噪效果,证明提出的改进阈值函数是有效的。
选择常用的小波基Sym4,该小波函数有着很好的对称性与连续性,可以使重构信号有更好的光滑性。分解层数过多会使信号中有用信息丢失严重,信噪比降低,分解层数过少则不能更好地去噪。而选择分解层数为4 层时,能够实现较好的去噪效果。
为了对去噪效果进行评价,本文选取均方根误差、信噪比表明去噪方法的优劣。均方根误差反映原始信号与去噪处理后信号发生的偏差程度,其值越小表明去噪效果越好;信噪比反映原始信号与噪声的比值,其值越大表明去噪效果越好。通过如下实验进行对比分析。
超声回波原始信号和含噪信号如图1 所示,去噪后的结果如图2 所示。
结果表明,与硬阈值、软阈值去噪方法相比,改进的小波阈值去噪后的信号与原信号较为接近,信号更加平滑。优化后的参数α为2,m为0.2。
均方根误差(RMSE)如表1 所示,信噪比(SNR)如表2 所示。
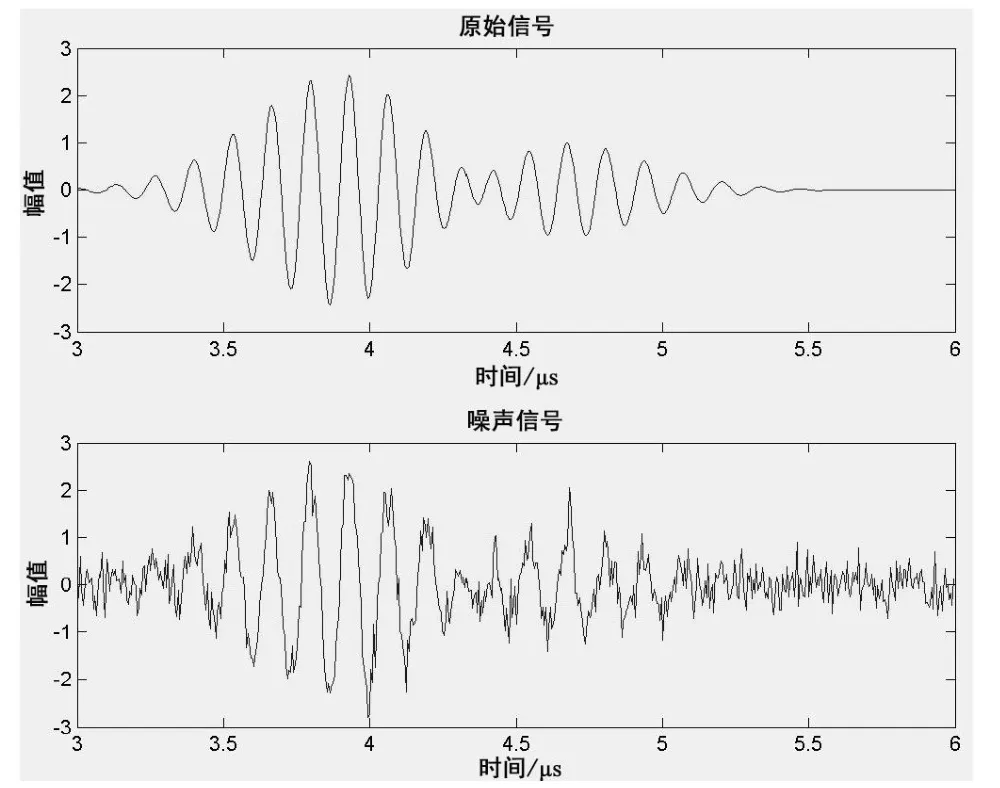
图1 原始信号与含噪信号
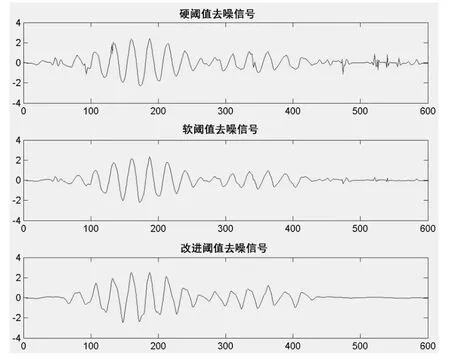
图2 不同阈值的去噪结果

表1 均方根误差(RMSE)比较

表2 信噪比(SNR)比较
通过对比即可发现,硬阈值函数的去噪效果最差,软阈值函数的去噪效果次之,而改进小波阈值函数的去噪效果最好,信噪比最高,均方误差最小,极大程度地去除了原始信号中的噪声成分。
4 结语
本文提出基于EEMD 的改进小波阈值函数去噪方法,能够更好地将信号中掺杂的噪声成分去除,信号更加光滑,较好地还原了信号的细节特征,使得信噪比提高、均方误差降低,从而提升了对信号的降噪性能。将该方法应用到多重超声兰姆波信号的去噪中,有着很好的去噪效果。
