多时滞马尔科夫跳变系统能量峰值控制方法研究＊

（江西理工大学，江西 赣州 341000）

1 引言

马尔科夫跳变系统是一类特殊的跳变系统，该类系统中各个模态之间的随机跳变符合一定的统计规律，即系统中各离散有限状态空间中的不同模态之间的转移服从马尔科夫过程。由于随机马尔科夫跳变系统能很好地描述一些实际系统，因此自从其被提出后，该类系统的稳定性分析与控制器综合问题就成为了控制理论研究与应用的热点之一。本文针对马尔科夫跳变系统中存在的多时滞现象，基于李雅普洛夫稳定理论研究该类系统的能量峰值稳定性分析与控制器设计方法。得到的相关定理均采用线性矩阵不等式描述，可以方便地通过Matlab线性矩阵不等式工具箱进行求解。

2 模型描述

多时滞马尔科夫跳变系统的状态方程描述如下：

式（1）中：x（t）、u（t）、ω（t）、z（t）分别为系统状态、控制输入、外部干扰信号输入及被控输出；A[r（t）]、Al[r（t）]、B[r（t）]、Bω[r（t）]及C[r（t）]为适当维数的已知矩阵；dl为系统时滞；r（t）为有限集合r（t）≜{1，2，3，…，N}中随机取值的马尔科夫随机过程，跳变转移矩阵为∏={πij}{i，j∈S}。

转移概率为：

式（2）中：h＞0且当j≠i时，表示从时间t的模态i到时间t+h的模态j的状态转移概率且有

定义1：对于ω（t）=0均有则马尔科夫跳变系统被称为均方渐进稳定。

定义2：如果存在一个常数γ＞0使得系统在u（t）=0的情况下均方渐进稳定，且在0初始条件x（t）=0，∀t∈[-τ，0]下，对于任意ω（t）∈L2[0，∞），均有则系统为能量峰值稳定。

定义3：如果存在控制器u（t）=K[r（t）]x（t）使得系统闭环状态下能量峰值稳定，则系统为能量峰值可镇定。

3 稳定性分析与控制器设计

定理1：对于给定γ＞0，如果存在正定对称矩阵Pi、Q1、U1，非奇异矩阵S，标量βi及γ1i＞0使得不等式成立，则系统为能量峰值稳定。

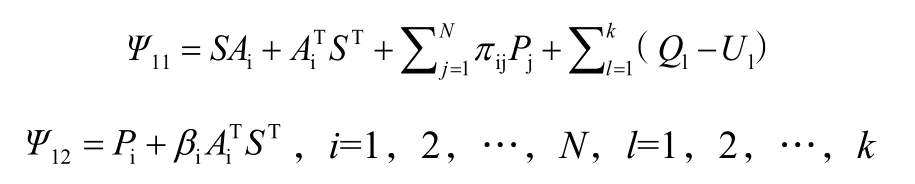
定理2：对于给定γ＞0，如果存在正定对称矩阵非奇异矩阵，标量βi及γ1i＞0使得不等式成立，则系统为能量峰值可镇定。

4 实例

考虑如下双模态跳变系统，系统包含两个时滞项，且有d1=0.1，d2=0.2，C1=C2=[0.10.1]，B1=B2=[21]T，Bω1=Bω2=

图1 来自EI Centro1940的地震激励信号

经计算机仿真可得开环状态响应曲线如图2所示。从图2可知开环状态下系统是发散的。

基于上文相关参数，现求解定理2可得不等式有解，且得到控制器增益矩阵：K1=[-1.3835-0.9067]，K2=[-1.5570-0.7945]

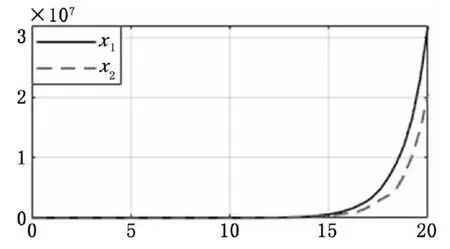
图2 开环状态下系统响应曲线

经计算机仿真可得系统在该控制器作用下的状态响应曲线如图3所示。从图3可知系统闭环状态下是稳定的，且有进而有即闭环系统满足能量峰值条件。

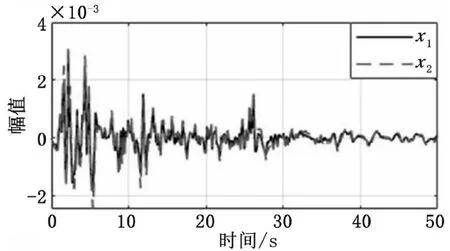
图3 闭环状态下系统响应曲线

5 总结

本文基于李雅普洛夫稳定理论及线性矩阵不等式技术研究了多时滞马尔科夫跳变系统的稳定性分析与控制器设计问题，得到了系统稳定及镇定控制器存在的充分条件，并通过实例验证了相关理论的有效性。得到的相关定理均描述成了线性矩阵不等式形式，可以方便地通过Matlab软件自带的线性矩阵不等式工具箱进行求解。