三维后向台阶不同宽高比对流动传热特性影响

沈洁惠，徐加辉，喜冠南

（南通大学机械工程学院，江苏 南通 226019）

1 引言

后向台阶管道内的流动与底面换热是一个经典的问题。其分离与再附现象出现在许多换热设备中，如电子冷却设备，核反应堆、涡轮叶片的冷却，突扩燃烧室及其他换热设备。这种流动在能源、动力、化工等工业领域都有着广泛的应用。因此对后向台阶内的流动与传热特性进行数值模拟研究对工程应用具有一定的理论指导意义。

1983年，文献[1]首先采用多普勒激光测速仪，对三维后向台阶（AR=36.7）中心面处的速度分布和再附长度进行了测量和分析，区分出层流（Re＜1200），过渡流（1200＜Re＜6600）和湍流（Re＞6600）三种不同的流动状态。Amaly的研究引起了国内外学者对后向台阶流的关注与研究兴趣。随后，国内外学者对后向台阶流进行了大量的试验[2-4]和数值模拟研究[5-8]。文献[9]初步研究了低雷诺数下不同宽高比对三维后向台阶的流动与传热特性的影响，在雷诺数（Re=500）、扩张比（ER=2）一定的情况下，对不同宽高比的底面努赛尔数和摩擦系数进行了比对分析，结果发现最大努赛尔数分布于台阶侧壁附近而不是台阶中央处。文献[10]对三维后向台阶再附着特性进行了数值模拟研究，并发现台阶侧壁处出现了回流的旋涡。文献[11]重点分析了低雷诺数下（50≤Re≤250））三维后向台阶管道内流动与传热特性的影响，并与二维后向台阶进行了对比。

综合已有文献可知，对三维后向台阶不同宽高比的流动特性研究较少，而结合流动与传热特性的研究更少。本次研究采用FLUENT软件，在数值模拟结果与实验结果相吻合的情况下，对比中低雷诺数下（100≤Re≤1200）不同宽高比的三维后向台阶（AR=4、8、12、16、24）流场内的流动与传热特性。

2 数值方法

2.1 数值模型与边界条件

三维后向台阶的计算区域，如图1所示。图中：S—台阶高度（10mm）；h—进口高度（9.8mm）；H—台阶出口高度（19.8mm）；W—台阶的宽度。台阶距离下游出口长度L=70S，扩张比ER=H/h=2.02，宽高比AR=W/S。

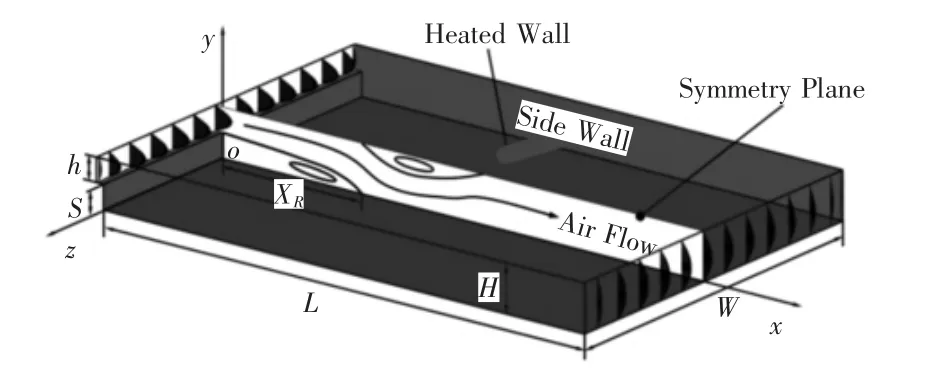
图1 计算区域Fig.1 Computational Domain

数值计算的边界条件：

（1）入口速度采用文献[12]提出的数学表达式（1）～式（4），编为UDF导入FLUENT中作为x方向进口速度条件，y和z方向的速度v，w都设置为0。

（2）出口处采用Outflow边界条件，速度梯度和温度梯度变化为0；

（3）流体进口温度T0=27℃，台阶的底面被等温加热TW=37℃，其余壁面为绝热；

（4）所有固体壁面满足边界无滑移条件；

（5）忽略粘性耗散。

2.2 控制方程

三维后向台阶管道内的流动介质是以连续、不可压缩的空气作为研究的对象。采用的控制方程具体如下：

质量守恒方程：

动量守恒方程：

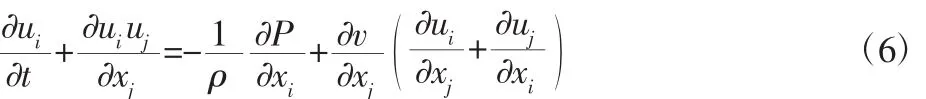
能量守恒方程：

式中：i，j=1，2，3—x，y，z三个方向；ρ—流体密度；P—压力；v—运动粘度；Cp—定压比热；T—温度；λ—热导率。

2.3 数值方法和网格划分

计算方法与网格划分方法已在文献[11]提出，整体网格视图与z截面放大网格视图，如图2所示。网格的密度对计算结果影响很大。如表1所示，在雷诺数为700，宽高比为8一定的情况下，选取三种不同网格尺寸计算其时均再附着长度和最大努赛尔数值。通过结果对比发现，随着网格数量的增加，时均再附着长度和最大努赛尔数值越来越接近密网格的数值。综合考虑计算时间及精度，选择网格节点为（270×40×70）作为计算网格。

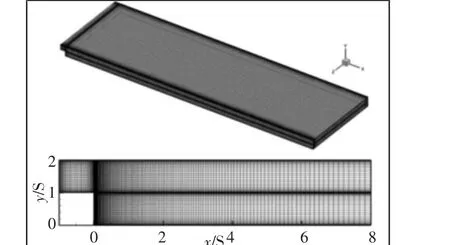
图2 整体网格与z截面放大网格视图Fig.2 The Whole Grid and the Magnified View of z-Plane

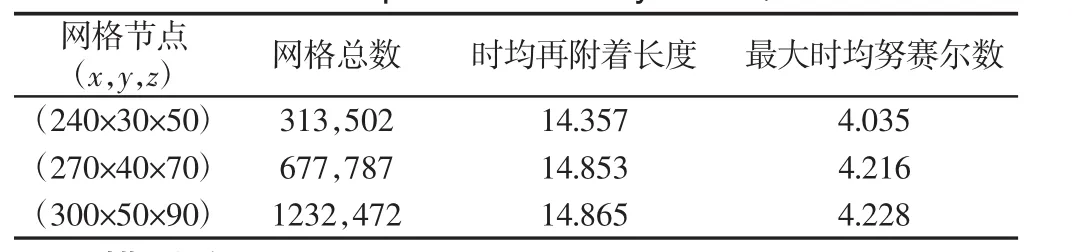
表1 网格无关性验证（宽高比为8，雷诺数为700）Tab.1 Grid Independence Study（AR=8，Re=700）

2.4 模型验证

为了验证模型计算的准确性，将数值模拟的结果与Amaly和Nie[13]的实验结果相对比。在雷诺数为525下数值模拟与实验的中心面处x方向不同截面的速度分布，通过结果对比发现两者之间具有较好的吻合性，如图3所示。由于本次数值模拟的进口速度假设为充分发展流动，雷诺数为190、343、512三种情况下中心面进口处x方向速度分布，如图4所示。通过对比发现进口速度的充分发展假设满足实际工况下的进口速度分布。

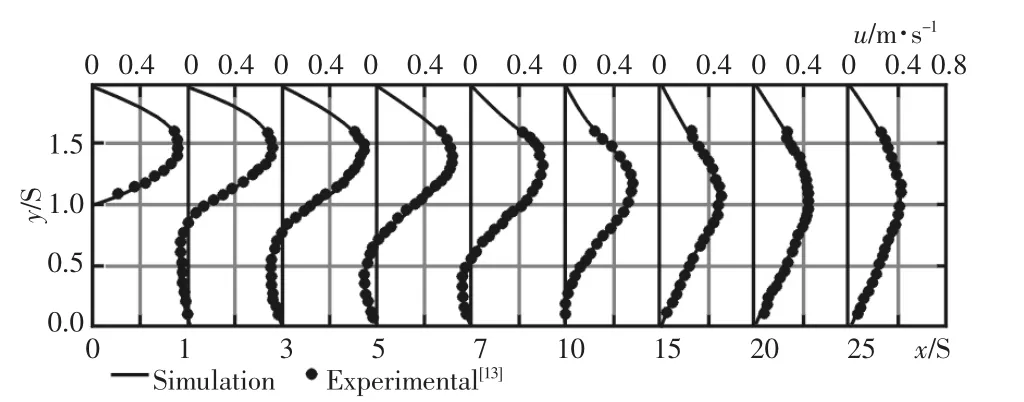
图3 Re=525中心面处实验与模拟的x方向速度分布对比Fig.3 Comparison of Experimental and Simulation Distributions of Stream-Wise Velocity for Re=525 at Symmetry Plane

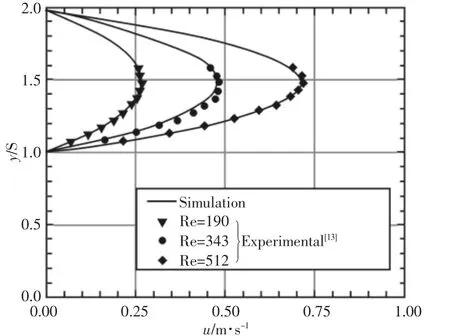
图4 中心面进口处x方向速度分布Fig.4 Distributions of Stream-Wise Velocity Component at Inlet Symmetry Plane

通常将壁面附近处x方向的剪切应力（μ∂u/∂y）为0作为再附着线。通过对比发现在雷诺数为343下，模拟与实验数据之间的误差很小。通过与实验结果的对比可以知道使用该计算模型得到的数值结果具有一定的可信度，如图5所示。

图5 雷诺数Re=343下底面再附着线分布Fig.5 Distribution of Reattachment Line at Re=343

2.5 无量纲参数

雷诺数：

式中：u0—进口平均速度；ρ—流体密度；μ—动力粘度；S—台阶高度。瞬态努赛尔数，时均努赛尔数及时空平均努赛尔数分别为：

式中：A—底面面积；α—底面单位面积；qW—底面热通量；τ—取样时间。

瞬态摩擦系数，时均摩擦系数及时空平均摩擦系数分别为：

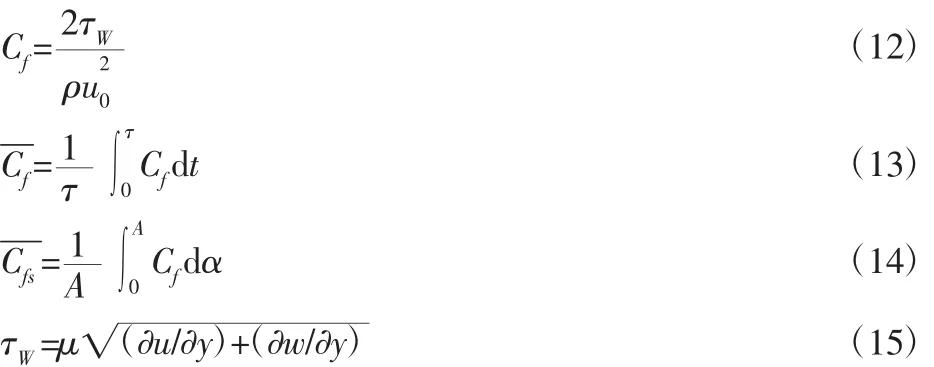
传热因子：

3 计算结果与分析

本研究主要总结中低雷诺数（200≤Re≤1200）和不同宽高比（AR=4、8、12、16、24）下的流动与传热特性，通过对比分析结果之间的具体特征变化。

3.1 顶面流动特性

三维后向台阶内流动具有对称性，故分析流动与传热特性时，选取一半区间来分析。在雷诺数为700条件下，不同宽高比的顶面流线和时均摩擦系数云图，如图6所示。通过对比发现，当AR=4时，出现逆向流动。当AR=8时，顶面出现旋涡流动，随着AR的不断增大，旋涡尺度变大且向着中心区域移动。云图中蓝色部分代表时均摩擦系数较小的区域，随着AR不断增大低阻区域的范围也在不断增大。

图6 雷诺数Re=700下顶面流线和时均摩擦系数云图Fig.6 Streamlines and Contours on the Up Wall for Re=700

3.2 底面流动与传热特性

在雷诺数为700条件下，不同宽高比的底面流线和时均努赛尔数云图，如图7所示。蓝色圆点代表最大时均努赛尔数的位置。通过对比发现，当AR=4时，底面传热明显较差。随着AR的不断增大，最大时均努赛尔数值不断增大且其位置向上游方向移动。在底面侧壁附近处，最大努赛尔数值位置附近出现了明显的回流运动，存在侧壁回流旋涡，洗刷侧壁附近，这也是最大时均努赛尔数分布在两个侧壁附近的原因[12]。对于底面努赛尔数值的局部分析，x方向侧壁附近（z/W=0.4）时均努赛尔数分布情况，发现AR不断增大，时均努赛尔数峰值不断增大，如图8所示。当AR达到24时，其结果与AR=16的结果没有明显变化。说明在同一雷诺数下，当AR达到一定值后，侧壁附近处的传热变化不大。由于管道宽度越小，中心部分加速效应明显，而侧壁附近的速度则相对较小，使得AR=4时侧壁处传热较差。AR增大侧壁影响逐渐减小，最终侧壁附近处的传热变化较小。以上通过雷诺数Re不变，改变宽高比AR，对比得出底面传热的不同特征。接下来主要对Numax的数值大小与其位置随雷诺数Re和宽高比AR变化的变化进行统计分析。不同雷诺数下及不同AR下的底面Numax数值变化，如图9所示。在雷诺数Re=200时，相互之间的差值不大。随着Re的不断增大，相互之间的差值变化明显。当AR=4时，Numax远低于其它AR下的数值，且随着Re的不断增大，Numax的数值没有明显增大；当AR=16，24时，两者 Numax较为接近；而当 AR=8，Re=1100时，Numax突然陡增越来越接近AR=12下的Numax。

图7 雷诺数Re=700下底面流线和时均努赛尔数云图Fig.7 Streamlines and Contours on the Bottom Wall for Re=700

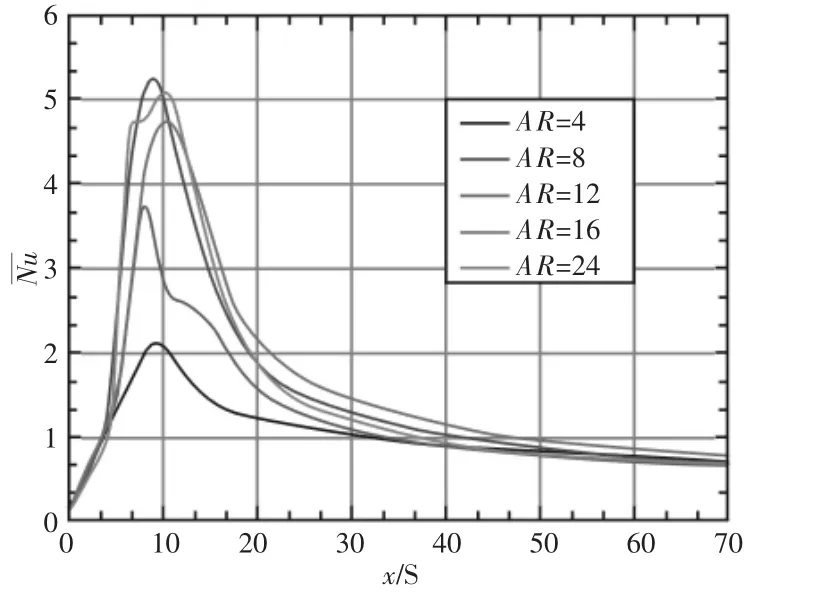
图8 雷诺数Re=700下侧壁附近时均努赛尔数分布Fig.8 N（u Distribution Near the Side Wall（z/W=0.4） for Re=700

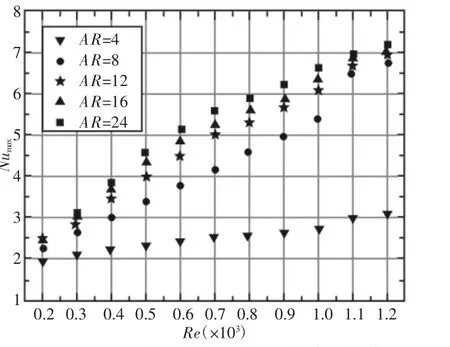
图9 不同雷诺数下底面最大时均努赛尔数值Fig.9 Numaxat the Bottom Wall for Different Re

不同雷诺数下Numax的x方向和z方向的位置分布，如图10、图11所示。当雷诺数Re≤1000时，Numax的x方向位置不断向下游移动。雷诺数一定时，AR越小x方向位置越远离台阶位置。当Re=1100时，在AR=8和16情况下，Numax的x方向位置向台阶上游移动。当Re=1200时，x方向位置向台阶下游移动。故Re=1100时的流动传热特性不同于其它情形，将在3.3节讨论。

Numax的z方向的位置分布，如图11所示。通过对比发现，随着雷诺数Re的不断增大，且在宽高比AR=8，12，16，24情况下，z方向的位置没有明显变化。这是因为AR一定的情况下，侧壁旋涡在z方向的尺寸几乎保持不变。只有在AR=4情况下，受加速作用影响，z方向的位置先不断向台阶侧壁移动，在Re≥600时，z方向的位置几乎保持不变。当AR越大，Numax的z方向的位置越靠近台阶侧壁，当AR大到一定数值，Numax的z方向的位置受宽高比AR的影响越小。

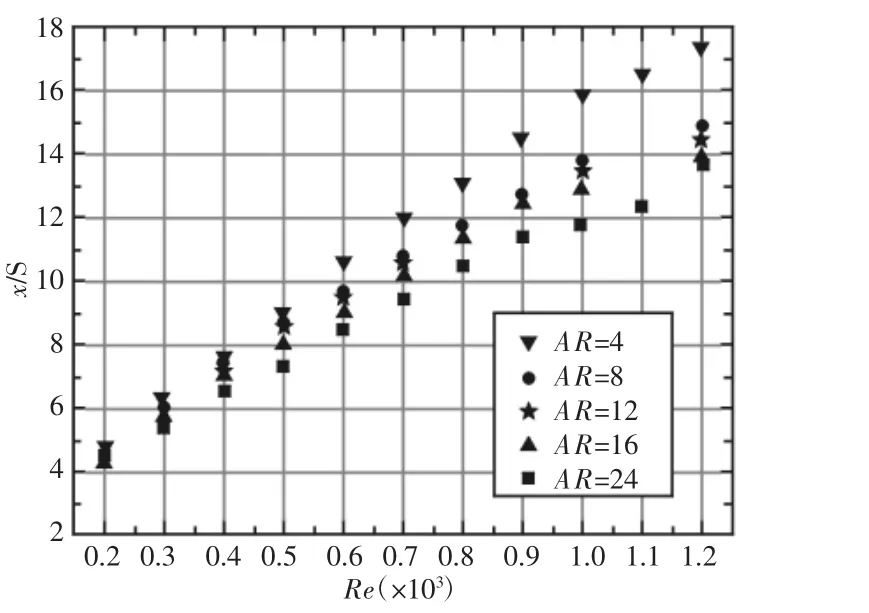
图10 不同雷诺数下最大时均努赛尔数值x方向位置Fig.10 Stream-Wise Direction（x-axis）of Numaxfor Different Re

图11 不同雷诺数下最大时均努赛尔数值z方向位置Fig.11 Span-Wise Direction（z-axis）of Numaxfor Different Re

3.3 底面传热强化特性

对于底面整体传热特性使用传热因子来体现，从图12发现在Re≤600，不同AR下的传热性能几乎一致。在Re≥600，且AR=4时，雷诺数Re不断变大传热性能越差。相反，在AR=8时，传热性能越来越高于其它AR下的传热性能。尤其在Re=1100时，AR=8，12，16传热因子值出现了陡增的状况，而在Re=1200时，传热因子值降低。不同雷诺数下底面时空平均摩擦系数，通过对比发现，宽高比AR对底面摩擦阻力影响较小。随着雷诺数Re的不断增大，时空平均摩擦系数不断减小并趋于平缓。在Re=1100时，AR=8情况下时空平均摩擦系数略高于其它情况。

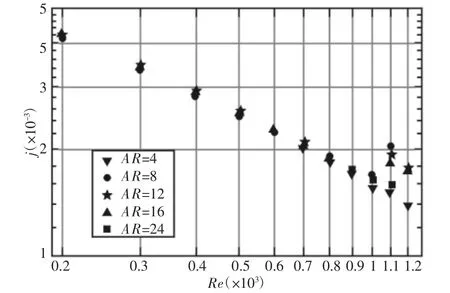
图12 不同雷诺数下传热因子值Fig.12 Value of j Factor for Different Re

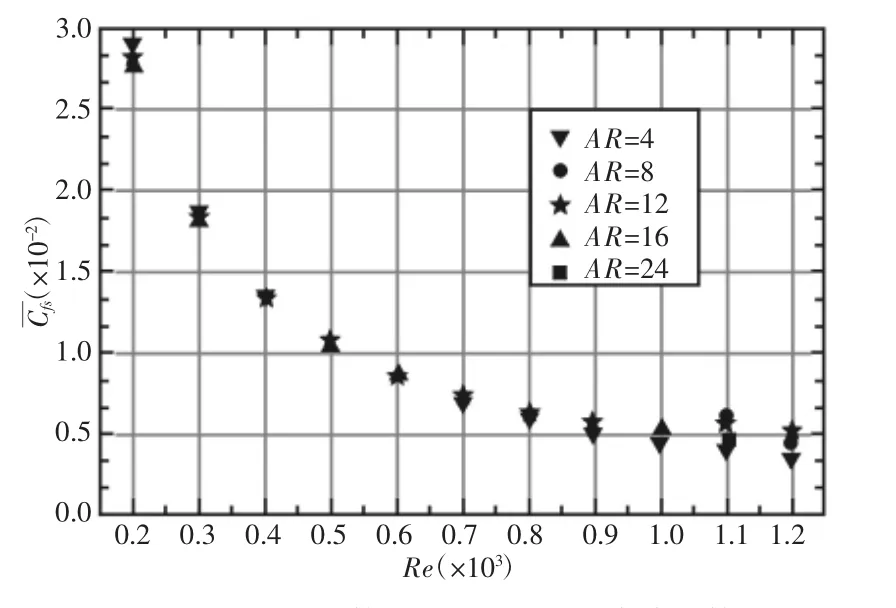
图13 不同雷诺数下底面时空平均摩擦系数Fig.13 Csfat the Bottom Wall for Different Re

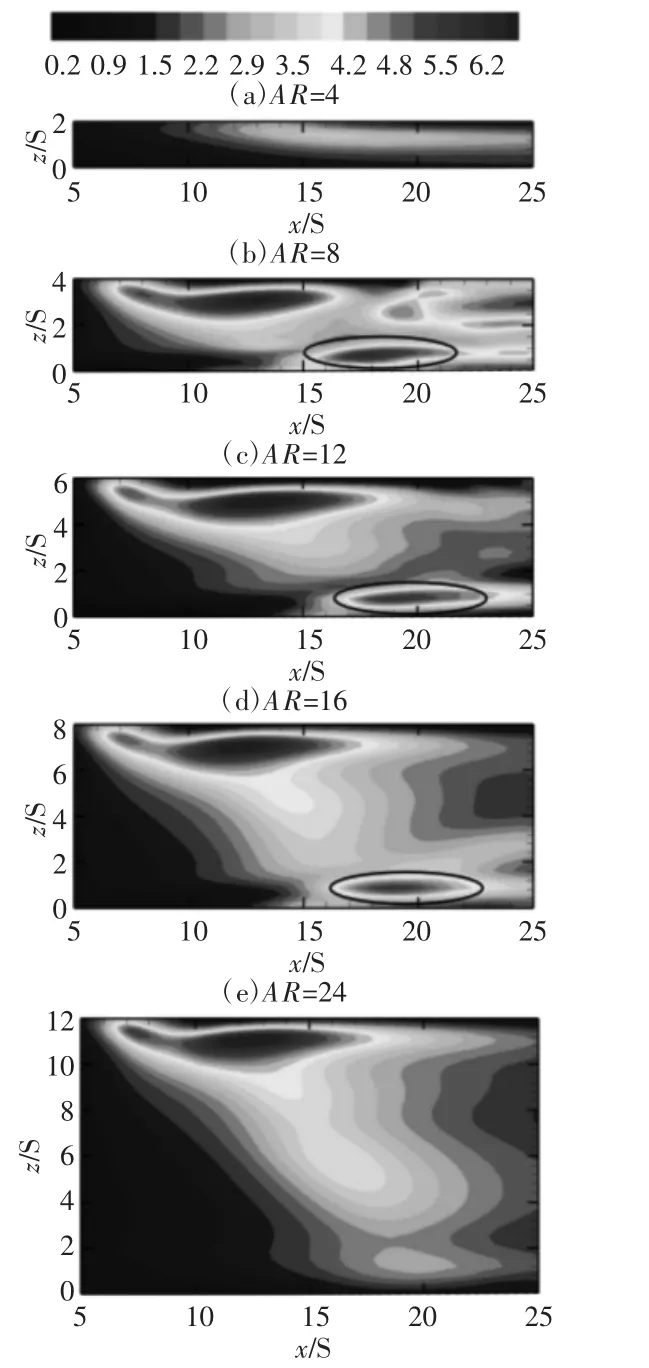
图14 雷诺数Re=1100下底面时均努赛尔数云图Fig.14 Nu Contours on the Bottom Wall for Re=1100

为了阐明Re=1100时，AR=8，12，16传热因子值出现了陡增的情况，雷诺数Re=1100下不同宽高比AR的底面时均努塞尔数云图，如图14所示。通过比较发现，AR=8，12，16时，在黑色椭圆内出现明显高努赛尔数红色区域。从AR=8情况开始，这一块区域的努赛尔数值随着AR变大逐渐变小。因为出现这种高努赛尔数红色区域使得在Re=1100时，AR=8，12，16情况下传热效果较好。

为了阐明椭圆区域内高努赛尔数红色区域形成机理，雷诺数Re=1100，AR=8下截面x/S=18速度矢量场及温度场云图，如图15所示。红色区域处为热流体，蓝色区域冷流体。在z/S为0到1.5区间内存在旋涡A和旋涡B，图中红色箭头为两个旋涡的旋转方向，蓝色箭头为最大努赛尔数的位置。旋涡A按照逆时针方向旋转，旋涡B则是顺时针旋转。由于旋涡A和B将上方的冷流体带到下方的热流体并与之混合，再将热流体按照旋涡运动方向带走，所以在两旋涡作用下，蓝色箭头位置处的温度边界层被破坏，此处的努赛尔数值也越大。由于旋涡A和B的作用使得图14中的椭圆区域内传热较好，这样底面整体传热性能得到提高。

图15 雷诺数Re=1100下截面x/S=18速度矢量及温度场云图Fig.15 Vector and Temperature Contours at x/S=18 Cross Section for Re=1100

4 结论

采用FLUENT，对中低雷诺数下（200≤Re≤1200）不同宽高比（AR=4、8、12、16、24）的三维后向台阶进行模拟计算，比对分析流场内的流动与传热特性，得到以下结论：

（1）当雷诺数Re一定，宽高比AR不断地增大，Numax不断增大且之间的差值越小；Numax的x方向位置不断向台阶上游移动；Numax的z方向位置不断靠近侧壁。

（2）当宽高比AR一定，雷诺数200≤Re≤1000区间内不断增大，Numax随之增大；Numax的x方向位置不断向台阶下游移动；Numax的z方向位置几乎保持不变。

（3）在雷诺数200≤Re≤1000，不同宽高比AR的情况下，底面传热效果及底面阻力大小没有明显变化。但在雷诺数Re=1100下，宽高比AR=8时，底面传热得到强化；宽高比AR=4时，底面传热效果较差。

（4）在中等雷诺数 Re=1100，AR=8，12，16 情况下，由于底面中心附近区域存在旋涡A和B将上方的冷流体带至底面并与热流体混合，使得传热得到强化。