空间桁架复合结构的阻尼减振分析与试验研究

王 鹏，张振伟，骆海涛，王正印

（1.东北大学机械工程与自动化学院，辽宁 沈阳 110819；2.中国科学院沈阳自动化研究所，辽宁 沈阳 110016）

1 引言

在实际工作生产中，桁架结构由于容易拆装、工艺性好、质量轻，且可以根据具体需要进行结构调节等优良属性得到了越来越广泛的应用。桁架的两个主要应用方面一个是在桁架的最顶端连接相关的光电学设备用来分离设备从而降低相互间的干扰，另一个是作为支撑结构支撑空间大型可展设备等。空间桁架复合结构主要由桁架和箱体两部分组成。箱体安装于桁架的末端，桁架起到连接和支撑的作用，箱体内部装载不同类型的精密光电学仪器。

桁架复合结构在工作和运输过程中所经历的振动环境主要分为随机振动环境和低频正弦振动环境[1]。这两种振动环境会使桁架结构遭到损坏，发生连接松散，结构件变形，性能下降的现象，同时这两种振动会使光电学仪器精度下降，机械疲劳，电路瞬间短路、断路，甚至功能失效。因此，对桁架复合结构振动特性及振动抑制的研究很有必要。

在低频正弦振动环境下根据实际需要采用在空间载荷箱体结构和桁架管状结构上敷加粘弹性约束阻尼层[2]的方法进行减振。粘弹性约束阻尼层形式简单，不需要改动现有结构，质量轻，粘贴方便，阻尼性能优越，使用较少的材料就能达到较大的减振效果[3]。桁架具有延展性，取其中一小段不仅便于研究，而且研究成果也可以应用到整个大型桁架中。

2 粘弹性阻尼材料

2.1 粘弹性阻尼材料的耗能机理

粘弹性材料大多是高分子聚合物。从微观角度来看，高分子聚合物是由庞大的分子链组成，分子间通过物理键或者化学键进行连接，当对它施加外力时，分子链会发生位置的移动，出现转动、伸缩、曲折的现象，当外力消失时，一部分分子能够回到原来的位置，同时返还了一部分外力做的功，这就是粘弹性材料的弹性性能的体现，一部分分子不能够回到原来的位置，产生了不可恢复的永久变形，这就是粘弹性材料的粘性性能的体现，同时外力做的功会变成热能释放出去，这就是粘弹性材料的耗能机理。从宏观上来说，当物体振动时，阻尼层也会随着一起振动，阻尼层在物体表面时而被压缩时而被拉伸，阻尼层和物体表面不断发生相对位移，由于摩擦阻力很大，使机械振动能量被消散或转换成热能被消耗掉。

2.2 粘弹性阻尼材料的结构样式

两种粘弹性阻尼的处理方式分为自由阻尼层和约束阻尼层，如图1所示。自由阻尼结构是将将一层一定厚度的粘弹性阻尼材料粘贴于结构层表面上，当结构层产生弯曲振动时，阻尼层随结构层一起振动，在阻尼层内部产生拉压变形而耗能，从而起到减振降噪的作用。约束阻尼结构是将粘弹性阻尼材料粘合在结构层和刚度较大的约束层（通常是金属板）之间，当结构层弯曲变形时，结构层与约束层产生相对滑移运动，粘弹性阻尼材料产生剪切应变使一部分机械能损耗掉。

图1 两种粘弹性阻尼层结构Fig.1 Two Kinds of Viscoelastic Damping Layer Structure

3 空间桁架复合结构

桁架复合结构仿真计算模型主要有以下几部分组成，如图2所示。它们分别是：箱体结构、长管、短管、连接件、连接方块、粘弹性约束阻尼层及工装。

图2 粘弹性阻尼桁架复合结构有限元模型Fig.2 Finite Element Model of Viscoelastic Damping Truss Composite Structure

粘弹性阻尼桁架复合结构上的阻尼层选用北京宇航材料研究所（703所）提供的成熟产品，材料为橡胶。约束层选用2A12板。阻尼层和约束层各自的材料属性，如表1所示。

表1 阻尼层和约束层材料属性Tab.1 The Material Properties of Damping Layer and Constrained Layer

通过模态分析，选择在模态应变能大的位置敷加粘弹性阻尼层，则结构振动的过程中阻尼层的剪切变形大，消耗的能量多。有限元模型网格单元采用三角形和四边形单元，连接方块和连接件采用体网格划分，其余部分采用壳网格的方式划分，阻尼层采用体网格，其节点位于单元的角点，约束层采用带偏置的壳网格，单元共用节点，有限元模型单元数386743，节点数193026，重16.20kg，如图3所示。

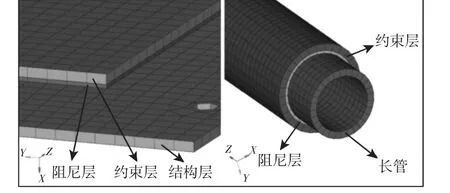
图3 粘弹性阻尼层敷加图Fig.3 Application of Viscoelastic Damping Layers

4 粘弹性约束阻尼层参数优化

减振方案中粘弹性阻尼层的敷加位置，敷加面积和剪切模量已经确定，针对阻尼层和约束层的厚度[4]制定了几种减振方案，以第一阶阻尼因子[5-8]作为减振评价指标，因为阻尼因子会随着阻尼层厚度的增加而增加，这里桁架结构上的阻尼层厚度取0.8mm，箱体结构阻尼层厚度取1mm。用Nastran提供的复特征值[9]计算功能可以较为方便的确定阻尼结构的阻尼因子大小，采用复模量模型，粘弹性材料的本构关系为：

式中：σ0和 ε0—随时间变化的简谐应力；E″（ω）—E″（ω）材料复模量；η（ω）—材料阻尼因子。

复合结构的振动方程为：

式中：M—质量矩阵；K*—复刚度矩阵；K和K′—复刚度矩阵的实部和虚部；u*—节点位移向量。

令 u*=φ*eiw*t，（3）式可以变换为：

式中：ω*—复频率；φ*—复特征向量；λ*—复特征值，式（5）通过QR矩阵分解求解后可得：

于是，第n阶模态阻尼因子ηn为：

式中：λn和—复特征值λ*的实部与虚部。

复特征值计算法能很好的描述粘弹性阻尼材料的动态力学特性[10]。减振方案和有限元计算结果，如表2所示。由有限元计算结果可以得到对于空间载荷箱体结构的粘弹性约束阻尼层，阻尼层0.8mm，约束层2mm，对于桁架结构粘弹性约束阻尼层，阻尼层1mm，约束层3mm时粘弹性阻尼复合结构阻尼因子增量最大，减振效果最佳。

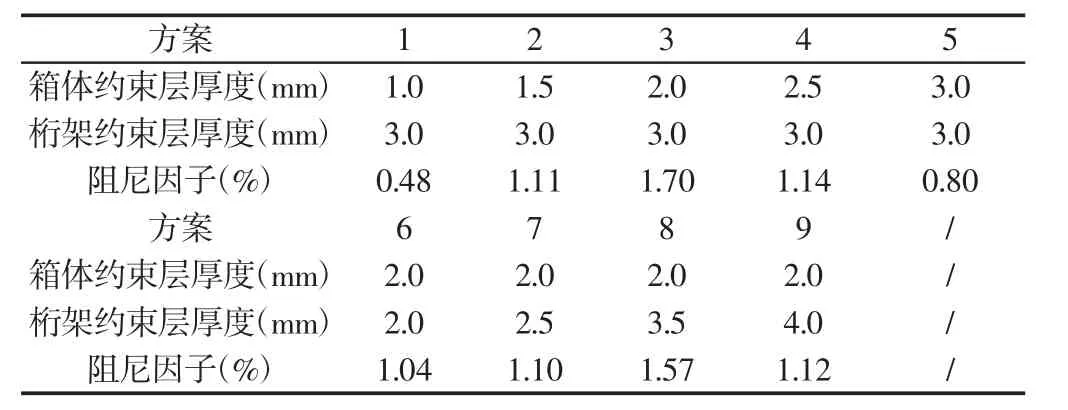
表2 粘弹性阻尼桁架复合结构减振方案及有限元计算结果的比较Tab.2 Comparison of Vibration Reduction Scheme and Finite Element Calculation Results of Viscoelastic Damping Truss Composite Structure

5 仿真分析与试验验证

5.1 正弦扫频分析

根据正弦验收级工况，具体试验条件，如表3所示。在Nastran中用模态扩张法分别对原结构和粘弹性阻尼复合结构的XYZ三个方向进行正弦响应分析，在空间载荷箱体结构的前盖板，左盖板，上盖板的几何中心表面位置各选取一点进行分析，并生成特定测点的加速度响应曲线。三维模型测点位置，如图4所示。

表3 正弦扫频振动试验条件（验收级）Tab.3 Sine Sweep Vibration Test Conditions（Acceptance Level）

图4 三维模型测点位置Fig.4 Position of Measuring Point in Three Dimensional Model

原桁架结构和粘弹性阻尼桁架复合结构的XYZ三个方向测点4912频率响应分析结果，如图5所示。通过有限元仿真分析，粘弹性阻尼桁架复合结构与原结构相比减振效果明显，其中，X方向测点19545加速度响应峰值由15.9g降为11.2g，测点27222加速度响应峰值由15.8g降为10.8g，测点4912加速度响应峰值由15.8g降为10.8g，整体加速度响应值由16.4g降为11.6g；Y方向测点19545加速度响应峰值由17.7g降为14.2g，测点27222加速度响应峰值由17.2g降为14.6g，测点4912加速度响应峰值由17.7g降为14.2g，整体加速度响应值由17.8g降为15.2g；Z方向加速度响应值最大，减振效果最明显，这也验证了粘弹性阻尼层对峰值有较好的减振效果，峰值越高，减振效果越明显，其中测点4912加速度响应峰值由86.8g降为21.4g，整体加速度响应值由87.1g降为21.4g。

图5 测点4912频率响应分析结果Fig.5 Frequency Response Analysis Results of Measurement Point 4912

5.2 振动试验

试验对象是原结构和粘弹性阻尼桁架复合结构，试验目的是通过振动试验分析得到原结构和粘弹性阻尼桁架复合结构在X、Y、Z三个方向上固定测点的加速度响应值，和仿真结果进行对比。正弦验收级输入条件，如表3所示。X方向振动试验图，如图6所示。原结构和粘弹性阻尼桁架复合结构的测点4912在XYZ三个方向振动试验分析结果，如图7所示。

图6 X方向振动试验Fig.6 X-direction Vibration Test

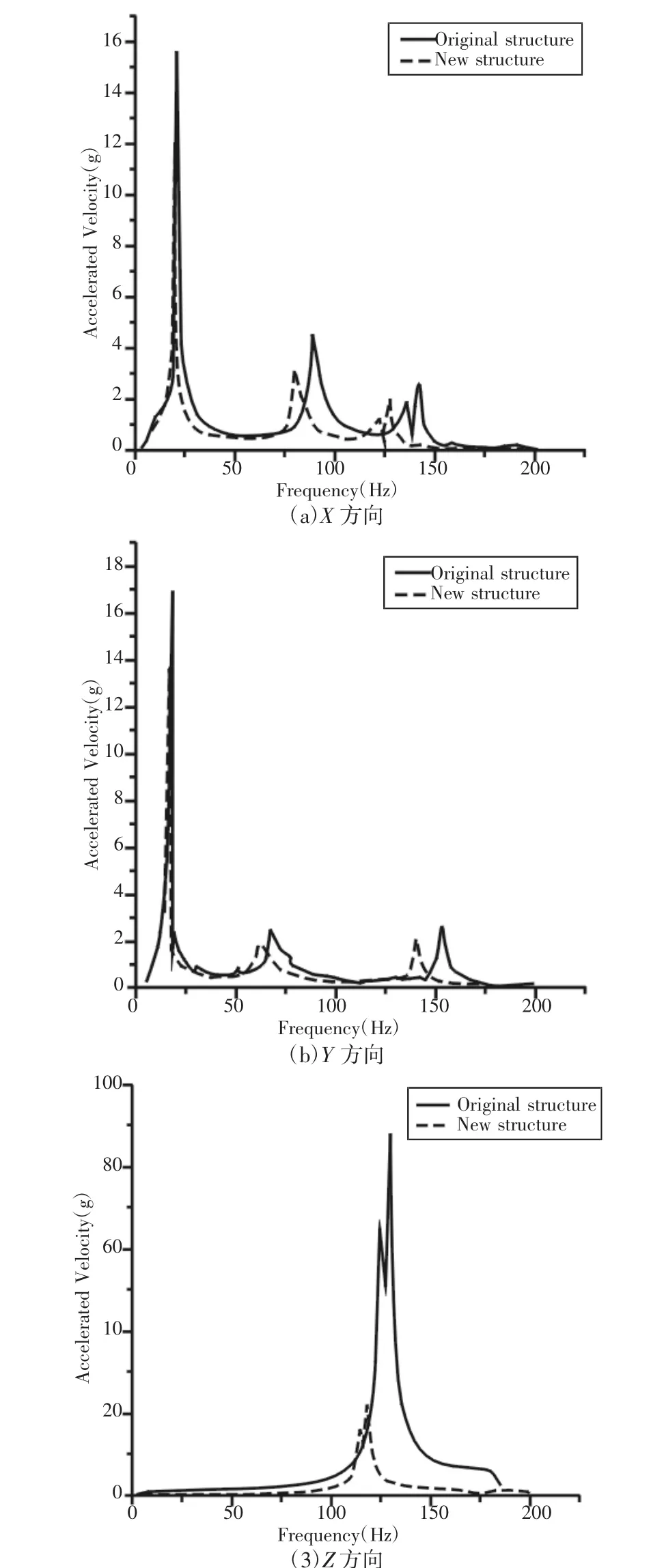
图7 测点4912振动试验分析结果Fig.7 Vibration Test Analysis Results of Measurement Point 4912

通过有限元仿真分析和正弦验收级振动试验数据对比，可以看出仿真和试验对应方向加速度响应值相差不大，其中原结构三个测点X方向加速度响应峰值仿真结果和试验结果相比最大误差8%，Y方向加速度响应峰值仿真结果和试验结果相比最大误差4.6%，Z方向加速度响应峰值仿真结果和试验结果相比最大误差2.8%。粘弹性阻尼桁架复合结构三个测点X方向加速度响应峰值仿真结果和试验结果相比最大误差6.9%，Y方向加速度响应峰值仿真结果和试验结果相比最大误差10.6%，Z方向加速度响应峰值仿真结果和试验结果相比最大误差1.9%。

6 结论

根据实际工程需要，在不改变原有设计结构的基础上采用敷加粘弹性约束阻尼层的方法对桁架复合结构进行减振处理，通过对原结构和粘弹性阻尼桁架复合结构进行仿真分析和试验研究可以得到以下结论：（1）采用复特征值法在有限元软件Nastran中以阻尼因子大小作为减振幅度评价指标对粘弹性约束阻尼层的设计参数进行优化，得到了粘弹性阻尼桁架复合结构的最优模型。（2）采用模态扩张法对原结构和粘弹性阻尼桁架复合结构进行频响分析，证明了粘弹性约束阻尼层对于桁架复合结构减振效果显著。（3）通过在正弦验收级工况下对原结构和桁架复合结构进行振动试验，得到有限元仿真和试验结果基本一致，验证了减振方案的可行性和有限元仿真分析的正确性，为粘弹性约束阻尼层的工程应用提供了一种分析方法。