EEMD结合概率神经网络的风力机轴承故障诊断研究

狄 豪，孙文磊，武玉柱

（新疆大学机械工程学院，新疆 乌鲁木齐 830046）

1 引言

风力发电机传动装置中的轴承以滚动轴承为主。据西班牙一家公司统计，齿轮箱是风力发电机故障率最高的零部件，因此对齿轮箱中的轴承故障进行研究具有重要意义。风力发电机工作环境比较复杂，运行工况多变，因此采集到的信号大多是非平稳非线性的，而且噪声污染严重。传统的时域和频域分析方法不能在非平稳信号的分析中取得理想的效果，因此许多学者研究了一些分析非平稳信号的方法。其中，短时傅里叶变换、Wigner-Villefen分布、小波和小波包分析等方法不同程度地对此类信号的时变性给予了恰当的描述。之后，文献[6]提出了新的用来处理非平稳、非线性的自适应性时频分析方法-经验模式分解（EMD）。但信号经EMD分解后得到的IMF分量会因模态混叠的现象而失真，因此文献[6]提出了总体平均经验模式分解（EEMD）的方法。该方法在消除模态混叠方面取得了很好的效果。滚动轴承在不同的故障状态下，频率范围不同时所对应的频带能量值也有区别，将不同状态下IMF频带能量占总能量的比值作为特征元素组成的特征向量可以区分轴承的不同的状态。概率神经网路具有学习速度快、处理能力强、识别正确率高的特点，将轴承不同状态下的特征向量输入其中，PNN可以通过对训练集样本的学习准确地输出测试集样本所对应的故障状态，可以作为滚动轴承故障状态识别的方法。

2 总体平均经验模式分解（EEMD）

EEMD是针对EMD存在的不足所做的改进算法，是一种噪声辅助数据分析方法[7]。高斯白噪声的频谱是均匀分布的，可以将原始信号分解成连续的不同尺度的IMF，以此达到抑制模态混叠现象的效果。EEMD的过程如下[6]：

（1）初始化参数：设置EEMD的总体平均分解次数N，添加高斯白噪声与原始信号的标准差的比值μ。

（2）在原始信号 x（t）中加入高斯白噪声 n（t）。

式中：x（t）—原始信号；n（t）—添加的高斯白噪声；x′（t）—合成后的信号。

（3）对添加了高斯白噪声后的信号EMD分解。

（4）将步骤（2）与步骤（3）循环N次，求出N次得到的IMF的均值，作为最后的IMF。

式中：imfn，i—最终经EMD分解的到的第i个IMF。

使用EEMD算法对齿轮箱轴承5种状态下的原始信号进行分解，得到不同状态下的IMF分量，滚动轴承不同故障时，信号的频带分布不同，计算各个故障状态下IMF能量与总能量的比值，把能量比当作特征向量的特征元素，得到轴承5种状态下的特征向量。特征向量是识别算法进行学习和检验识别算法识别正确率的样本的集合。

3 概率神经网络（PNN）

概率神经网络是一种前馈型神经网络，是一种基于贝叶斯最小风险准则（贝叶斯决策理论）与概率密度函数估计方法的并行算法。概率神经网络一般由输入层、模式层、求和层和输出层组成，其结构[5]，如图1 所示。

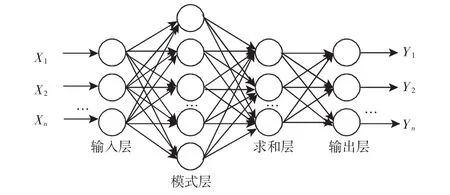
图1 PNN的结构图Fig.1 PNN Structure Diagram

来自训练样本的值输入到输入层，输入层把特征向量传递到网络[9]。输入层通过权值ωij与模式层连接，模式层进行计算，算出特征向量与不同模式的匹配关系，所有训练样本数之和等于模式层神经元个数。模式层把输入样本进行加权求和，经过非线性算子g（zj）运算后传输到求和层。

该层每个模式单元的输出为：

式中：X—输入样本；

Wi—输入层与模式层之间的连接权值矩阵；

δ—平滑因子[10]。

求和层把属于某类的概率累加，即：

式中：m—样本数目。

滚动轴承的不同状态分别对应一个求和层单元，把对应状态的模式层单元的输出相加[9]。

输出层也是决策层，由阈值辨别器组成。输出层神经元是一种竞争神经元，不同神经元对应轴承不同的状态，接收求和层输出的各类密度函数，输出层神经元个数与故障类型的种类数相等，概率密度函数最大的神经元输出1，其余神经元输出0。

得到特征向量后可以用概率神经网络进行学习与识别。从轴承不同状态下的特征向量中选出一部分特征向量作为训练集供概率神经网络学习，剩余特征向量作为测试集样本检验识别算法的识别正确率。当测试集样本输入到概率神经网络中，神经网络会将其与训练集样本中的特征向量进行对比分析，然后准确识别出该测试样本属于哪一种故障类型。

4 实验分析

在某大学的风机实验台上完成实验。使用的是Spectra Quest公司生产的风力发电机传动实验台，完成风机齿轮箱轴承的保持架、滚动体、内圈、外圈故障的模拟实验。使用的滚动轴承型号为ER-16K，每次将不同的故障零件安装到齿轮箱轴承中进行实验。实验台主要部件，如图2所示。

图2 风力发电机传动实验台Fig.2 Wind Turbine Transmission Test Bed

异步电动机的转速由变频器控制，变频器显示的频率是电动机的理论转频，扭矩的大小由磁粉制动器控制。把高速轴的理论转频设置为30Hz，变频器显示实际转频29.6Hz。故障模式有保持架、滚动体、内圈、外圈故障4种，再加上正常状态，一共采集5种状态的原始信号。采样频率设置为5000Hz，采样时间设置为1s，扭矩施加大小设置为22N·m。实验用的数据采集卡为4通道数据采集卡，加速度传感器安装在齿轮箱3个互相垂直的方向上。每种状态的原始信号采集10组。

以滚动体故障信号为例，对原始信号进行EEMD分解，添加高斯白噪声与原始信号的标准差的比值是0.3，总体平均分解次数为500次，得到的IMF分量，如图3所示。

图3 滚动体故障信号EEMD分解Fig.3 Rolling Body Failure Signal EEMD Decomposition

以上为滚动体故障信号经EEMD分解后得到的12个IMF分量。信号经EEMD后得到的IMF分量里其实仍有无意义的分量，如图3中最后几个分量就是低频分量还有残余分量，所对频率也无意义。将这些分量也作为特征元素会造成干扰，使识别算法的识别正确率降低。因此需使用相关系数法过滤掉不重要的IMF分量，设置好系数的阈值，分量的系数比阈值小则被当作不重要的分量。计算公式如下：

计算结果，如表1所示。

表1 滚动体故障IMF相关系数Tab.1 Rolling Element Failure IMF Correlation Coefficient

将相关系数小于0.02的IMF分量去掉，保留前8个IMF分量作为有意义的分量。

滚动轴承在不同的故障状态时，频率范围不同的时候所对的频带能量不相等，因此可以把不同状态下的频带能量的不同当作特征在故障诊断时使用。IMF频带能量的计算公式如下：

式中：N—采样数点目；

n—采样点的序列 n=1，2，…，N；

IMFi（n）—第i个IMF分量。

信号的总能量按公式计算：

其中，M=8。

计算各个IMF分量占总能量的比：

把能量比当作特征向量的特征元素构建特征向量，以滚动体故障为例可以计算得到如下的故障特征向量，如表2所示。

表2 滚动体故障特征向量Tab.2 Rolling Body Failure Characteristic Vector

同理可以得到滚动轴承在正常，保持架、内圈、外圈故障时的特征向量，每种状态含有10组特征向量，部分结果，如表3所示。

表3 部分特征向量Tab.3 Partial Characteristic Vector

得到轴承5个状态的特征向量后，可以把这些特征向量作为样本进行故障状态的识别。

将特征向量输入到概率神经网络模型中，每种状态随机选取6组数据作为训练样本进行学习，剩余样本作为测试样本进行识别，由于训练样本和测试样本都是随机选取的所以每次测试的结果都不一定相同，测试6次的结果，如表4所示。

表4 概率神经网络的测试结果Tab.4 Probabilistic Neural Network Test Results

其中，正确率最高的一次识别结果，如图4所示。

图4 PNN识别正确率最高的一次结果Fig.4 The PNN Identifies the First Result with the Highest Accuracy

图中：1—正常状态；2—保持架故障；3—滚动体故障；4—内圈故障；5—外圈故障

极限学习机（Extreme Learning Machine，ELM）也是一种前馈性神经网络，具有学习速度快、泛化性能好的特点，使用极限学习机的识别结果，如表5所示。

表5 极限学习机的测试结果Tab.5 Extreme Learning Machine Test Tesults

其中，正确率最高的一次识别结果，如图5所示。

图5 ELM识别正确率最高的一次结果Fig.5 ELM Recognizes the Highest Accuracy of the First Result

对比极限学习机的识别结果，可以发现概率神经在识别正确率上有着明显优势，识别正确率较高，可以作为滚动轴承故障识别的方法。

5 结论

该文研究了EEMD结合频带能量计算的风力发电机齿轮箱轴承的故障特征提取方法和使用概率神经网络的故障状态识别方法，通过对轴承在正常、保持架、滚动体、内圈和外圈故障状态下的实验分析，结果表明：原始信号经EEMD后可以减小模态混叠现象，得到的IMF分量的频带能量与总能量的比值可以准确反映不同状态的特征信息。得到特征向量后分别使用概率神经网络与极限学习机进行训练识别，发现概率神经网络在识别正确率上有优势。因此提出的方法具有有效性。