FDM技术中基于层轮廓特征的路径规划方法研究

2020-06-20王占礼周天诣陈延伟

机械设计与制造 2020年6期

王占礼，周天诣，陈延伟，任元

（长春工业大学机电工程学院，吉林长春 130012）

1 引言

熔融沉积成型即 FDM（Fused Deposition Modeling）[1]，是快速成型技术中的一种。FDM工艺是将工程塑料ABS、聚乳酸PLA等材料通过高温融化成熔融态，通过挤出机构挤出，按指定的分层厚度以及规划好的路径，在立体空间上层层堆积形成三维实体[2]。其中打印过程的前处理存在两个关键步骤，即：对三维实体模型进行分层和对每一层截面按一定的路径规划方式进行填充[3]。在现有主流路径规划方法中，有针对提高成型精度的路径规划，如（1）轮廓偏置路径规划：熊文俊提出了向心收缩偏置路径规划[4]，程艳阶提出了判断环相交的办法[5]。（2）螺旋线路径规划，如张建华提出的螺旋线扫描与简单直线扫描相结合，提出了扫描线共区判据[6]。（3）并行栅格路径规划：如黄小毛提出了并行栅格路径规划[7]。（4）分形路径规划：如淡卜绸提出的基于Hilbert填充曲线的自由曲面刀具路径规划[8]。有针对提高制件力学性能的路径规划，如（5）光栅路径规划：如靳晓曙提出了光栅路径规划[9]。为此提出一种基于层几何轮廓特征的路径规划方法，即针对分层后截面的轮廓特征采用不同的路径规划方法，目的在于提高3D打印的成型精度和提升打印效率。

2 层轮廓几何特征的定义

STL文件格式是快速成型技术通用的三维图形文件格式，被STL文件表达的数据模型是由无数个三角面片逼近原来的三维实体得到的，而分层算法的实质就是以一个既定高度的平面来求取与平面相交的各三角面片的交点，再将交点顺次链接，由于平面与平面的交点是一条直线，而无数条直线连成的平面几何图形为多边形，故路径规划的实质就是针对不同形状特征的多边形进行不同方法的填充。为了表述截面轮廓特征，定义了饱满度和充盈度两个特性参数，其饱满度为截面轮廓的周长与面积的比值，用η表示，其公式如式（1）所示。

式中：C0—最外环截面轮廓的周长；S0—最外环截面的面积；Si—第i个内环所围成的面积；Ci—第i个内环轮廓的周长。

其充盈度为最外环截面面积S0与其最小包围矩形Sb的比值，用符号￡表示，其公式如式（2）所示。

以上两参数有如下性质：

（1）饱满度η为无量纲量，η的值只与截面的形状有关，而与图形大小无关。

（2）充盈度￡为无量纲量，其取值范围为［0，1］。

通过对“单片机原理与接口技术”教学实践的探讨，并且进行改革和实践，不断地调整教学内容，改进教学方法，提高学生动手操作的能力，使越来越多的从业大学生在研发和售后服务中发挥他们的专业特长，受到各领域用人单位的好评。实践证明“单片机原理与接口技术”培养了学生解决实际问题和创新的能力，在有利于全面推进教学改革的同时，也增强了能力，增长了自己的见识，也让学生们更加的自信。但是“单片机原理与接口技术”还有很多需要改进的地方，还需要教师们不断地进行探索。

（3）η 越大，截面越“苗条”，￡越大，图形越规则。

3 路径规划方法研究

在研究了前述现有的5种主流路径规划基础上，同时又研究了三角形分形路径规划、普通蜂巢路径规划。各种路径规划方法分述如下。

3.1 三角形分形路径规划

分形名词最早是由哈佛大学物理系教授Benoit于1975年提出的，自相似原则与迭代生成原则是分形理论的重要原则，它们在通常的几何变换下具有不变性，也可以无穷递归。而三角形分形路径规划即是分形曲线的一种特殊情况，即利用层轮廓边缘曲率的变化来迭代三角形填充线，以适应由于曲率变化所引起的狭小空间填充问题。填充后的效果，如图1（a）所示。三角形分形路径规划由于在饱满度充盈度较好的截面能节省大量的填充空间，故在相同打印条件下采用此种路径规划方法能提高打印效率。

3.2 Hilbert曲线路径规划

Hilbert曲线填充均匀，能避免自相交，具有自相似性，可无穷递归。通常用Lindenmayer方法在计算机上生成分形曲线，用动态二维数组来记录每一次递归后的XY坐标，通过编写左改写函数与右改写函数来实现路径与边界的布尔运算，用控制字dir实现路径方向上的改变，用正余弦函数来实现不同方向上的前进量，用L，R分别表示直线左右方向上的变化。Hilbert曲线生成路径，如图1（b）所示。由于Hilbert曲线是从起点到终点的迷宫式路径，其前进方向是不断变化的，随着递归次数的增加，曲线更为复杂，大量的短线段构成了扫描路径，因此避免了长线扫描填充造成的翘曲变形，提高了打印制件的打印精度。

3.3 普通蜂巢路径规划

此种路径规划填充方法为普通蜂巢的正六边形，无自相交，具有自相似性，本质上讲属于分形曲线的一种。即当分形曲线相似维度为2时，路径规则采用不同的构造方法，即不同的LR字符串排序，同样可以生成分形曲线，普通蜂巢路径规划，如图1（c）所示。由于蜂巢结构是覆盖在二维平面的最佳拓扑结构，其基本几何单元正六边形密合度最高、所需材料最简，改进的普通蜂巢路径规划由于填充线无自交，故蜂巢填充在制件的成型强度和成型精度要优于其他路径规划方法。

3.4 阿基米德螺线路径规划

阿基米德螺线也称等速螺线，得名于希腊数学家阿基米德。阿基米德螺线所描述的运动过程实际上是一个点匀速离开另外一个点的过程，而在离开的过程中又以固定的角速度围绕该点做圆周运动，最后合成的轨迹方程成为阿基米德螺线，其极坐标方程为：

图1 路径规划方法示意图Fig.1 Schematic Diagram of Path Planning

3.5 offset偏移路径规划

阿基米德螺线路径规划是向外偏移，而偏移路径规划是向内偏移，其主要流程为判断内外轮廓轮和判断廓环的方向、偏移直线的生成、自相交的去除等。偏移路径规划算法较为复杂，但熔丝按偏移路径沉积有助于消除因熔丝冷却所产生的内应力，有助于提高打印制件的精度。

3.6 并行栅格路径规划

并行栅格路径规划已由黄小毛博士提出，将一分区的栅格扫描线按照一定的规则分成若干组栅格，加工时分别加载各组栅格的填充线，其路径规划基本原理为：（1）扫描线编组分号；（2）扫描线端点偏移；（3）扫描线首尾相连；（4）末点处理。并行栅格路径规划较往复直线路径规划省去了喷头在跨越相邻填充线时的回抽，使扫描线更加连贯，相对于往复直线路径规划节省了打印时间。

3.7 光栅路径规划

光栅路径规划的基本方式为两组互相交错的平行线，相邻两层的扫描线错开一定的角度，一般为垂直分布，且在边界线内作锯齿形往复扫描，光栅路径规划扫描方法简单，可靠性高，程序便于实现。光栅路径规划由于存在交点的重复填充问题，故不利于提高制件的打印精度。

以上所述7种路径规划方法已在CURA软件上二次开发成功并生成G代码，为了提升打印效率，采用GCodeSimulator软件实现了打印过程的仿真，旨在清晰的了解每种路径规划所需要的时间，便于从合理缩减打印时间的角度选择合适的路径规划。同时，为了提高制件的打印精度，将不同路径规划方法生成的G代码输入到熔融沉积成型3D打印机，验证各路径规划方法在具有不同轮廓特征的截面上打印精度的差异。

4 基于层轮廓几何特征路径规划的时间仿真

对于不同的层轮廓特征，从饱满度、充盈度两个指标考虑，给出的四个截面轮廓，并拉伸37.5mm高度为打印样本，如图2所示。其截面基本属性，如表1所示。

图2 零件建模示意图Fig.2 Schematic Diagram of Parts Modeling

表1 零件截面属性表Tab.1 Parts Section Property Sheet

将4个零件按前文的7种路径规划方法分别生成不同的G代码，并用GCodeSimulator软件进行打印过程仿真，其三角形分形路径规划和Hilbert曲线路径规划仿真结果，如图3所示。其余7种路径规划方法的仿真结果，如表2所示。

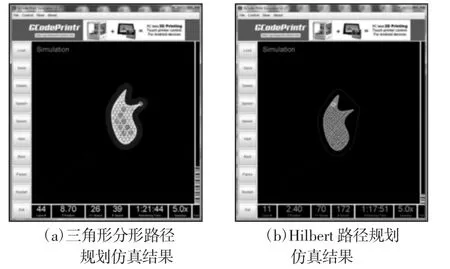
图3 G Code Simulator仿真结果Fig.3 G Code Simulator Results

表2 不同路径规划打印仿真时间一览表Tab.2 Different Path Planning Printing Simulation Time List

从打印时间的仿真数据可以得到下面初步结论：

（1）对于饱满度较小但充盈度较大的截面采用三角形分形路径规划可提高打印效率。

（2）对于饱满度较大但充盈度较小的截面采用并行栅格路径规划、普通蜂巢路径规划同样可以提高打印效率。

5 基于层轮廓几何特征路径规划实验验证

实验所选用的3D打印机为I3 Prusa打印机，如图4所示。

图4 I3 Prusa打印机Fig.4 I3 Prusa Printer

其机器参数，如表3所示。

表3 打印机参数表Tab.3 Printer Parameter Table

实验采用单挤出喷头，喷嘴直径为0.4mm，设置层高为0.2mm，首层层高0.1mm，线宽0.35mm，壁厚1mm，顶层/底层后2mm，填充密度50%，喷头挤出温度200℃，热床温度40℃，回抽距离6.5mm，回抽速度25mm/s，打印速度60mm/s，成型材料为PLA丝材，丝材直径 1.75mm，密度为 1290kg/m3，弹性模量为（3000～4000）MPa，线材收缩率为0.2%。将7种路径规划生成的G代码输入到3D打印机中打印，统计打印实物与理论模型的翘曲变形数值差异，得到各路径规划对于不同层轮廓的打印精度影响，其零件1打印效果，如图5所示。将打印成型的制件放置在室温条件下1日之后，用千分尺分别测量每一个零件XY平面方向的最大翘曲变形量Δt，每个零件测量三次取平均值，其结果，如表4所示。