EEMD_H与ITLBO_SVM相结合的滚动轴承故障诊断方法
2020-06-20蔡振宇包珊珊
蔡振宇,张 敏,包珊珊
(西南交通大学机械工程学院,四川 成都 610031)
1 引言
滚动轴承广泛存在于机械结构中,作为重要的旋转机构,是最容易出现故障的部件之一,其中,振动信号具有非线性与非稳定的特性,包含各种噪声信号和振动信号,因此单从时域或频域实现准确的故障诊断是非常困难[1]。文献[2]利用集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)分解信号,提取模态函数(Intrinsic Mode Function,IMF)分量的均方根和重心频率作为特征变量,选取特征的信息仍有不足,数据信息代表性不强。Hilbert包络解调是一种运用广泛的信息解调技术,但在确定带通滤波参数时需要丰富的经验,限制该技术的发展[3],若直接在模态函数的基础上进行Hilbert变换则可避免带通滤波参数的确定,同时又可研究信号的幅值包络、瞬时相位和瞬时频率。
目前对支持向量机(Support Vector Machine,SVM)参数优化较好的算法有遗传算法(GeneticAlgorithm,GA)、粒子群算法(Particle Swarm Optimization,PSO)等及其改进的算法,但都存在类似的问题,GA与PSO极易早熟,陷入局部最优解,且计算量大,稳定性差,迭代收敛时间过长等缺陷。教与学算法(Teaching-Learning-Based Optimization,TLBO)是由文献[4]在 2011 年提出的一种新型群体智能算法,通过教师阶段和学生阶段不断的提高学生成绩。教与学算法具有参数少,算法简单易理解,求解精度高等优点,但教师阶段的学习因子过于随机,不利于局部细微搜索,以及学生学习内容不能过于信任,易陷入局部最优。引入改进的教与学算法优化SVM参数模型,采用EEMD_Hilbert进行数据处理提取特征变量,代入ITLBO_SVM故障诊断模型内,实现高效故障诊断。
2 故障特征提取
2.1 集合经验模态分解
利用白噪声频谱均衡分布特点,EEMD通过给目标信号加入一定幅值的高斯白噪声来均衡噪声,可以有效解决EMD出现模态混叠的现象。EEMD可对各种非线性和非稳定的信号进行准确处理,其分解具体步骤如下:
(1)随机生成μ为0,σ为en的高斯白噪声nm,设定原始参数,M表示EMD分解次数,m表示第m次分解,1≤m≤M。
(2)将高斯白噪声nm(t)加入待处理的信号y(t)中,得到信号为ym(t),即为:

(3)将合成信号ym(t)进行经验模态分解分解后得到S个IMF 分量 cs,m(t),cs,m(t)表示进行第 m 次 EMD 分解后的第 s 个IMF分量;

式中:S—分解得到IMF的个数;rm—第m次EMD分解后的余
项;cs,m(t)—按频率进行降序排列。
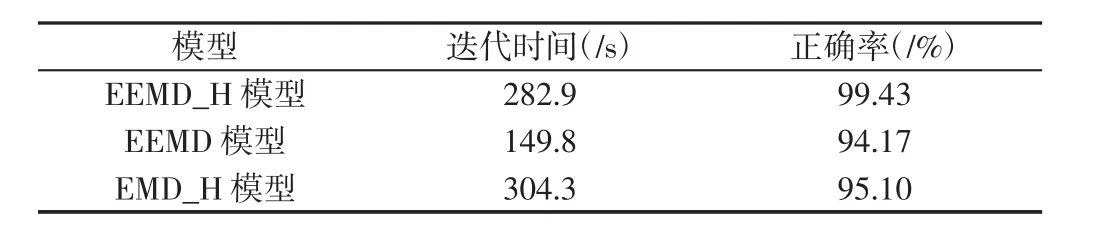
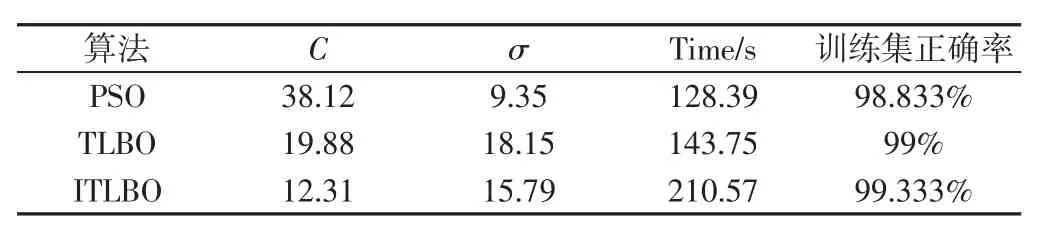
(4)若 m (5)计算进行M次EMD分解后得到每个IMF分量的均值,根据不相关随机序列统计均值为0,消除加入高斯白噪声对真实IMF分量的影响,即为: 信号进行EEMD分解得到若干个顺序为降次的IMF,选取前几个作为研究对象,后面以残存低频噪声为主,不予考虑。对选取的模态函数进行Hilbert变换,解调原理如下: 滤波器公式: 将前几个主要IMFS及其解调信息作为特征提取对象,为有效提取特征值,挑选合适的统计特征值来对处理的信息进行特征提取,选取的统计特征值依次是均值、峰值、极差、标准差、偏度、峰度、变异系数和平方和。 综合上述统计特征量,特征维度较高,采用核主元分析(Kernel Principal Component Analysis,KPCA)对特征维度进行特征降维,便于后面快速故障诊断。考虑篇幅问题不对KPCA降维具体内容进行论述,详细参考文献[5]。 支持向量机通过核函数来实现实现线性不可分向线性可分的转化,研究表明径向基核函数在SVM中表现出良好的泛化能力,其形式,如式(7)所示。 把满足具有多维样本输入和一维样本输出原则的向量,作为输入向量从原来的空间映射到高维特征空间H,并在该特征空间H内建立优化超平面。分类线方程如下[6-8]: 式中:ω—权值;x—输入向量;b—阈值;l—向量的个数。 根据Karush-Kuhn-Tucker,优化各个系数得到最优分类函数: 适应度函数则为: 由式(11)可知进行SVM分类模型构建时,性能的关键因素在于惩罚参数C和核函数σ的选取。 3.2.1 教师阶段 假设班级总人数为H,学生科目数为J,算法迭代次数为k,Mj,k为学生在j科目下的平均水平。选择当前适应度值最好的个体作为教师来实现教学阶段。式(12)为科目j当前学生平均水平与教师水平之间的差。 式中:rk—(0~1)的随机数;Xj,hbest,k—在科目 j时教师的水平。TF=round[1+rand(0,1)]—教学因子,取值为 1 或 2。 教师阶段各个个体进行更新,如式(13)所示。 各个体更新后,若 xj,h,k的适应度值优于 xj,h,k,则接受 xj,h,k,反之则接受 x′j,h,k。 3.2.2 学生阶段 学生阶段通过个体与个体互相学习来提高整体学习水平,分析两两个体之间的学习差异进行学习更新。该阶段学生学习更新由式(14)给出。 式中:学生P≠Q,在当前迭代次数为k时各对应的学习水平为分别为 Xj,P,k和Xj,Q,k在教师过程教导后的更新值,优化目标函数为(fx)。若新解对应的适应度值优于,则选择更新后的反之则选择 3.3.1 教学因子的改进 在算法学习前期,个体与个体之间差异较大,而学习后期整体水平相差不大。基本TLBO算法选择TF时采用随机0或1,较大的随机性让算法前期和后期都存在很大的动态性。因此为保证算法前期和后期能分别实现稳定的全局搜索和局部细微搜索,引入改进教学因子,具体由式(15)给出。 3.3.2 权重因子的引进 算法前期,学生学习能力强,接受知识内容较多;算法后期学生学习疲惫,记忆能力减弱,所接受的知识内容较少;教学阶段和学习阶段两者所接受的知识能力也有所差别,教师教授学生知识能力较强,相比于学生个体之间的相互学习所接受的知识内容要更多,因此引入两种信任权重[9]。 式中:ω1、ω2—教师阶段和学生阶段的信任权重;Kmax—最大迭代次数;k—当前迭代次数。教师阶段解的更新式(13)引入信任权重ω1,如式(18)所示。 引入信任权重ω2后,对学生阶段更新过程式(14)进行修改,如式(19)所示。 利用EEMD将原始信息分解成若干个IMF,再对其进行Hilbert变换得到IMFS的解调信息;对两者信息集进行统计特征提取;由于特征维数过多,计算时间与效果会变差,采用KPCA进行特征再次提取,获取最佳的特征信息;最后采用ITLBO_SVM构造诊断模型进行多分类故障诊断。 采用美国CaseWesternReserveUniversity电气工程实验室的滚动轴承实验平台数据[10]进行仿真实验研究,实验设备包括电机、转矩传感器、功率计和电子控制设备。该实验测试的轴承是选自SFK公司生产的6205-2RS深沟球轴承,并对实验的轴承进行电火花加工,以模拟点蚀故障,故障点分别在内圈、滚动体及外圈上。 本选取滚动轴承在转速为1797r/min,采样频率为12kHz情况下的正常工作、内圈故障、滚动体故障和外圈故障四种不同状态下工作中的滚动轴承振动数据信息,其中外圈故障这里选择选择发生在6点钟方向上。并且同时考虑三种故障状态下的三种损伤尺寸,分别为0.178mm,0.356mm,0.533mm。 4.2.1 不同信号处理方法的对比研究 方法a将信号进行EEMD_Hilbert变换得到模态函数及瞬时频率,对其进行8个统计特征量提取,再进行KPCA降维,记为EEMD_H模型。方法b与方法a类似,不同在于不进行Hilbert变换,直接对模态函数进行统计特征提取,记为EEMD模型。方法c对原始信号进行EMD分解,后面处理方法和方法a一样,记为EMD_H模型。三种特征提取方法提取的特征数据代入PSO优化SVM参数模型进行分类,最后进行对比研究。粒子群算法初始参数:种群数20,最大迭代数400。结果,如表1(数据结果为10次平均值)所示。同一信号分别进行EEMD和EMD分解之后选择首个IMF进行图像化的波形图,如图1所示。 表1 三种分类结果Tab.1 Three Classification Results 图1 两种方法首个IMF图Fig.1 Two Methods the First IMF Graph 利用PSO优化SVM参数做最后结果分析而不用提出的ITLBO算法优化SVM参数,是为单纯说明该特征提取方法的优越性,控制变量因素而不引入其他因素。图1能看出EEMD在分解信号时可以较好避免EMD分解信号的模态混叠现象,且从表1可得出EEMD_H方法正确率更高。不进行Hilbert变换处理的数据没有加入变换后频率数值,数据维数少一部分,进行降维后维数变少,因此以迭代时间缩短,但正确率却并不理想,比加入Hilbert变换数据要差5%多,说明加入Hilbert变换使提取特征信息更全面,能达到更好的数据特征提取。 4.2.2 不同参数寻优迭代收敛的对比研究 利用目前成熟的粒子群算法PSO优化SVM参数构造的诊断模型与TLBO和ITLBO优化SVM参数构造的诊断模型进行对比,各优化算法参数,如表2、表3所示。 表2 算法参数设定表Tab.2 Algorithm Parameter Setting Table 表3 ITLBO、TLBO与PSO对SVM参数寻优Tab.3 ITLBO,TLBO and PSO Optimization of SVM Parameters 图2 三种算法SVM参数迭代对比Fig.2 Three Algorithms SVM Parameters Iterative Comparison ITLBO和TLBO算法区别就在于加入了自适应学习因子、信任权重,ITLBO利用自适应教学因子来控制学习速度,在教师阶段和学生阶段加入学习信任权重,平衡全局搜索和局部搜索,随着迭代次数越高,搜索区域就越细微,精确度就会提升到最高,使得训练集正确率更高。由于ITLBO算法引入自适应学习因子,学习速度在一定程度上有所减弱,但从图2可以看出,算法在很小的迭代次数下就能收敛到最优,因此可以在缩短最大迭代次下提高时间效率,可以达到高效寻优。PSO算法迭代时间适中,但正确率最低。ITLBO算法能在较短的迭代次数下收敛到最高的训练集正确率,且能跳出局部最优,最后实现更好的故障诊断。因此综合考虑,ITLBO算法迭代效果更好,更适合SVM参数寻优问题。 4.2.3 不同模型故障诊断的对比研究 利用粒子群算法PSO和TLBO分别优化SVM参数构造的模型与改进的教与学算法ITLBO优化SVM参数进行对比,分别记为PSO模型、TLBO模型和ITLBO模型。各算法初始参数设置,如表2所示。改进算法的权重和上述设置一样。将处理好的训练集和测试集代入构造好的模型,进行结果分析结果,(数据为10次实验值)如表4所示。ITLBO模型比TLBO模型和PSO模型诊断正确率分别高0.15%、0.25%左右。极差、方差越小说明数据越稳定,表4可以看出ITLBO极差和方差都最小,且十次平均正确率最高,可以说明改进算法不仅将故障诊断率优化到最高,而且效果更稳定,TIBO次之,PSO效果最差。改进TLBO相比基本TLBO来说,引入自适应教学因子、信任权重和加快学习速率能很好的优化算法本身的缺陷,实现更好的SVM参数优化。综上表明ITLBO算法对SVM参数优化可以很好的实现滚动轴承故障诊断。 表4 三种分类结果Tab.4 Three Classification Results 提出一种采用集合经验模态分解、Hilbert变换的特征提取方法,并利用ITLBO优化支持向量机分类参数的滚动轴承故障诊断方法。将振动信号进行EEMD分解,避免了EMD分解的模态混叠现象,准确提取信号特征;通过对IMFS分量进行Hilbert变换获得频域统计特征,综合了Hilbert处理数据的优点,避免带通滤波参数的选取,实现原始信号特征更准确提取;最后利用ITLBO算法优化SVM参数,在基本TLBO算法里引入自适应教学因子、信任权重对算法进行改进,使算法在全局搜索和局部搜索达到一个很好的平衡,比TLBO和PSO识别率更高、效果更加稳定。案例分析的结果证明,运用该算法模型在故障诊断方面是一条可行的途径。
2.2 Hilbert包络解调原理

2.3 统计特征提取与降维
3 基于ITLBO_SVM故障诊断
3.1 支持向量机




3.2 教与学算法

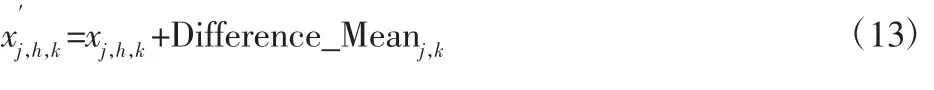
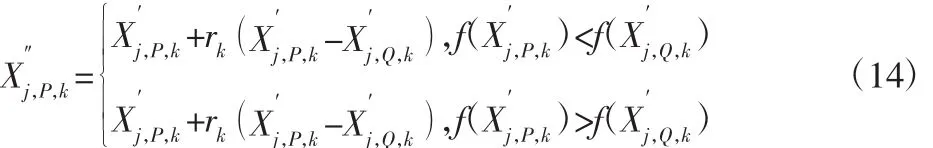
3.3 改进的教与学算法



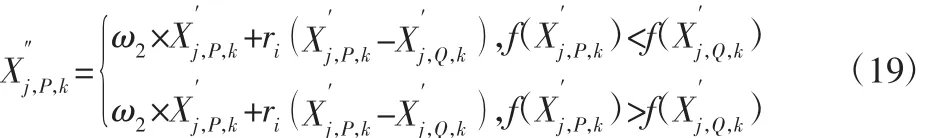
3.4 滚动轴承故障诊断
4 案例分析
4.1 数据特征样本
4.2 各种方法结果对比研究




5 结束语
