冗余度机械臂零初始关节速度的运动规划方案研究
2020-06-20徐剑琴李克讷
徐剑琴,李克讷,杨 津,张 增
(1.广西科技大学工程训练中心,广西 柳州 545006;2.广西科技大学电气与信息工程学院,广西 柳州 545006)
1 引言
冗余度机械臂的运动规划和控制是机器人学研究中一个很有吸引力的领域[1-7]。机械臂的逆运动学求解问题是其中一个核心的研究内容。对于冗余度机械臂,其逆运动学求解问题又称冗余度解析问题[7]。而基于伪逆的运动规划方案则是对该问题较为有效的解决方法之一。考虑到伪逆法具有结构简单和易于实现的特点,许多研究学者提出了不同的基于伪逆的优化方案来实现冗余度机械臂的运动规划和控制[7]。在实际工程应用中,机械臂的关节速度应尽量减少突变。特别是在机械臂开始运动的瞬间,较大的关节初始速度意味着关节从零突变到较大的速度。这种情况会对关节电机形成机械冲击和电流冲击,甚至可能损坏机械臂。而且,电机的构造和惯性作用也使得速度无法突变,势必产生速度误差,从而造成末端执行器产生位置偏差,影响任务执行精度,甚至可能导致整个任务失败。因此,如何有效解决机械臂的非零初始关节速度是冗余度解析中值得研究的一个问题。但目前少有文献报道该问题的研究情况。文献[5]基于二次规划方法提出了一种利用速度极限约束方法实现关节零初始速度运动,但主要针对机械臂的末端速度为零的自运动情形;文献[7]提出了一种将最小速度范数方案和最小加速度范数方案进行加权组合的优化方案,避免关节速度和关节加速度过高的现象,其重点是使得机械臂的关节速度在运动末态时接近零;文献[8]提出了一种补偿冗余度机械臂关节角从而达到补偿机械臂位姿误差的方法。但这些方法无法直接用以解决关节初始速度非零问题。在关节初始速度非零情况下,采用速度连续技术约束机械臂关节从零初始速度开始运动,并考虑末端执行器期望轨迹与实时位置之间的误差,求解出相应的关节速度向量。为此,提出了一种基于伪逆的冗余度机械臂零初始关节速度的运动规划方案,主要分以下三部分讨论说明:首先,给出冗余度机械臂运动的数学描述和提出了一种基于伪逆的关节速度约束调整方法;然后针对末端执行器执行任务时产生的位置误差,给出误差的补偿方法;最后,采用MATLAB对该方案进行仿真以验证方案的可行性和有效性。
2 机械臂的运动规划方案
2.1 关节速度的优化
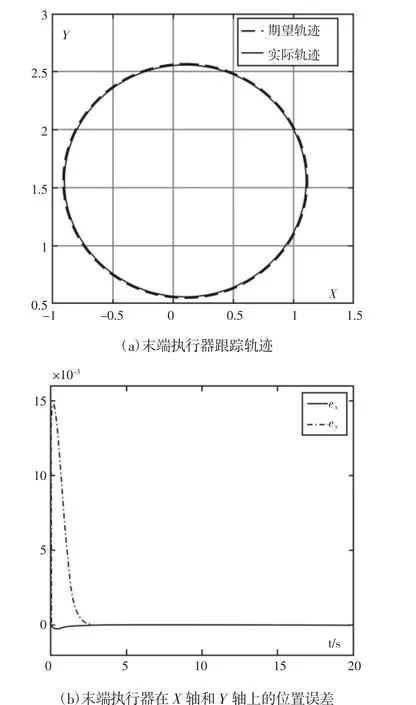
对于m 为了避免产生较大的非零初始关节速度对电机造成冲击,可采用一种速度连续技术使机械臂关节速度能从零开始连续增大,即引入一个时变函数j(t): 式中:τ>0—控制电机升速过程的标量系数,可根据电机性能和实际需要进行设定。 显然,当t≥0,函数值会由0开始随时间t递增,且迅速趋向于1,即j(t)∈[0,1)。因此,可通过连续函数j(t)对关节速度θ˙(t)进行约束以获得实际可实现性的零初始关节速度。结合式(1)和式(2),并取向量z为零向量,设计关节速度为: 显然,θ˙*(t)可随时间t由0逐渐变化并收敛于(t)。 综上所述,对于基于伪逆的冗余度解析方案,可用时变函数j(t)来约束关节速度,使之形成初值为0的连续过渡区,以更好地控制冗余机械臂,且具有简单和数学易处理的特点。 因初始关节速度非零突变问题导致的速度误差将传导到末端速度,并形成末端位置误差。如果没有及时对该位置误差进行消除或减小,那么它将存在于整个任务的执行过程中,影响轨迹跟踪精度,甚至会导致任务失败。为了解决这一问题,可采用以下位置误差补偿方法[10]。 为了更快地减小误差,使误差函数(4)收敛于0,设计d(t)的时间导数如下[10]: 式中:λ0≥0—可任意设置的标量系数。 将式(5)移项,得: 设末端执行器在t=t1时的位置误差为d(t1)=r(t1)-rd(t1)。把式(6)进行积分运算,并结合条件 t=t1时,d(t)=d(t1)进行整理,可求得: 可见当t→∞时,d(t)→0,r(t)能随时间按指数规律收敛到 把式(7)对时间求导,整理得: 即 t→∞ 时,d˙(t)亦收敛至 0。 综上所述,机械臂末端执行器速度可以综合为: 在本节中,以平面四连杆机械臂分别跟踪圆形和螺旋线曲线轨迹为例,对基于伪逆算法的零初始关节速度运动规划方案进行MATLAB仿真,以讨论和分析该方案的有效性。该机械臂相关参数如下:n=4,m=2,冗余度为 n-m=2,四个连杆的长度为 l=[l1,l2,l3,l4]T=[1,0.8,0.7,0.5]Tm。 设机械臂末端执行器需要跟踪一个半径r为1.0m的圆形轨迹,该圆形的参数方程为: 其中,ω=2π/T,任务执行周期取T=20s,机械臂的初始关节角向量为[2π/3,-π/3,-π/3,0]Trad。 图1 伪逆算法(1)求解所得的运动曲线(t=(0~5)s)Fig.1 Profile with Pseudoinverse Algorithm(1)(t=(0~5)s) 由伪逆算法(1)对圆形方程在速度层上进行反解仿真可知,机械臂在跟踪期望轨迹过程中,X轴上的位置最大误差值为ex=9.077×10-6m,Y轴上的位置最大误差值为ey=3.626×10-6m,机械臂很好地完成轨迹跟踪任务。此种情况下,实际轨迹和期望轨迹之间的实时误差非常小。但关节速度的初始值并不为0。截取t=(0~5)s时段的θ˙曲线,如图 1 所示。其中,θ˙(0)=[-0.047613,0.107128,0.138552,0.057730]Trad/s。由于电机在实际运动时,速度不能突变,因此,采用式(3)对关节速度θ˙进行约束。仿真实验结果,如图2所示。 图2 加时变系数j(t)约束后的仿真情况Fig.2 Simulation Results with Time-Varying Coefficient j(t) 从仿真结果可见:采用时变系数j(t)进行约束后,关节速度θ˙*的初始值为 0,且在任务开始时的一小段时间内||随时间平滑增大。但从图2(b)可看到,机械臂的实际跟踪轨迹已明显偏离期望轨迹,误差绝对值增大较快,在t=0.3783s时误差值ex=-0.0002456m,ey=0.0157m,即开始任务后的瞬间就产生较大的误差,且持续存在到任务结束。该误差主要是由于机械臂被约束从零初始速度而不是从较大的期望速度开始运动而引起的。值得注意的是,在实际情况下,机械臂控制电机的速度只能从零开始快速增大到控制值,如果直接采用伪逆算法(1)的反解结果也必然会导致末端执行器出现较大位置误差。为了减少该位置误差的影响,把关节速度优化方法(3)与位置误差补偿方法(8)相结合,即约束关节初始速度为零且考虑位置误差补偿的情况,取λ0=2进行仿真验证。结果,如图3所示。由图3(a)可见,实际跟踪轨迹与期望的任务轨迹基本重合。位置误差曲线,如图3(b)所示,Y轴方向上的位置最大误差值发生在t=0.1964s,ey=0.01492m,X轴方向上的位置最大误差绝对值发生在t=0.281s,此时ex=-0.0002258m;随后误差绝对值迅速减小,在 t=2.337s时 ex=-1.287×10-6,ey=6.727×10-5m;t=3.087s时ex=-7.915×10-8m,ey=9.879×10-7m。结合图和数据表明,实际跟踪轨迹在很短时间内快速且平滑地向期望的任务轨迹收敛,且位置误差非常小。仿真结果证明了该方案的有效性。 图3 取时变系数j(t)、λ0=2时的仿真情况Fig.3 Simulation Results with Time-Varying Coefficient j(t)and λ0=2 综上所述,当冗余度机械臂末端执行器跟踪给定的圆形轨迹时,计算机仿真结果表明,采用基于伪逆的冗余度机械臂零初始关节速度的运动规划方案,选择合适的j(t)、λ0,方案能起到有效的且较好的跟踪性能。其中,j(t)使得关节速度获得零初始值,而λ0是在轨迹跟踪过程中减小位置误差快慢的调节因子。值得一提的是,时变系数j(t)表达式里的参数是影响轨迹跟踪初期的关节速度和位置误差的重要因素,在实践中可以根据硬件来设计适当小的参数。 在该节中,期望末端执行器跟踪一螺旋线轨迹,该螺旋线的参数方程是: 机械臂的关节角向量初始值为[π/2,-π/4,-π/3,0]Trad,任务执行周期为T=20s,轨迹参数ω=2π/T,r=1.4m。对螺旋线轨迹跟踪的仿真情况讨论如下。 图4 优化后末端执行器在X轴和Y轴的位置误差Fig.4 Position Error of the End Effector in X and Y Axis After Optimized 设置λ0=2,优化后的关节角θ和关节速度θ˙*是平滑的、连续变化的,并且θ˙*的初始值已约束为0。从图4的位置误差曲线可以看出,由于关节速度θ˙*被约束为从0开始连续变化,使得在末端执行器跟踪期望轨迹的初期,跟踪轨迹出现了较大的误差。位置最大误差绝对值发生在t=0.21s,此时有ex=-0.08517m,ey=0.05165m。随后误差绝对值均迅速减小,在t=2.756s时ex=-4.645×10-6m,ey=2.752×10-5m;t=3.367s时 ex=-5.667×10-8m,ey=6.916×10-7m。显然,机械臂能自动调节,使末端执行器的运动轨迹能在较短时间内收敛于期望轨迹。综上所述,从跟踪圆形和螺旋线轨迹这两个实例可以看出,所提出机械臂零初始速度的运动规划方案能够提供一种灵活、有效的方法来使得关节从零初始速度开始平稳地执行任务,降低机械冲击,减小对电机的损害;并且在任务期间,若跟踪轨迹发生偏离,也能迅速地自动调整,使机械臂尽快收敛到期望轨迹。值得指出的是,将关节初始速度不为零的情况进行仿真实验,以供说明和讨论,而实际中,初始速度为零或不为零的情况都有,仿真实验验证运动规划方案对这些情况均能有效、准确和灵活地进行调整。 针对冗余度机械臂在执行轨迹跟踪任务时出现的初始关节速度不为零这一问题,提出了一种基于伪逆的冗余度机械臂的运动规划方案。该方案约束机械臂关节从零速度开始跟踪期望轨迹,并能及时减小执行任务期间产生的末端执行器位置误差,保证机械臂成功跟踪期望轨迹。利用平面四连杆机械臂进行MATLAB仿真,在设置参数λ0=2时,末端执行器位置误差在t≈3s时达到10-7m精度,仿真结果表明了所提方案的可行性和有效性。


2.2 位置误差补偿方法






3 仿真研究
3.1 圆形轨迹跟踪
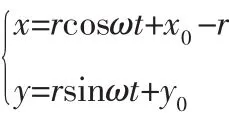


3.2 螺旋线轨迹跟踪
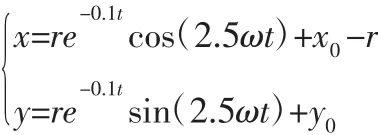

4 结论
