接触面积参数不确定对电机模态影响的研究

苏德赢，华春蓉，闫 兵，张胜杰

（1.西南交通大学机械工程学院，四川 成都 610031；2.成都华川电装有限责任公司，四川 成都 610106）

1 引言

电磁噪声是电机的主要噪声源之一，其对电机的NVH性能有重要影响。但是在电机生产过程中，仍存在同一型号的不同电机模态不一致的问题，这给电机电磁噪声的控制带来了困难[1]。

目前对于电机模态的研究大部分是基于确定性电机模型的研究，文献[2-5]建立了较准确的电机模态有限元模型，并采用锤击法验证了有限元模型的正确性。但是，加工和装配误差导致电机各零件间接触面积存在不确定性，且电机零件材料密度、弹性模量等物理属性也存在不确定性，这些都影响了电机模态的一致性[6]。目前对不确定电机模态的研究较少，文献[1]采用锤击法测试了5台同一型号电机的模态固有频率，并分析了零部件及整机模态固有频率的均值与方差。文献[6]初步分析了零件材料刚度和接触面积参数对电机模态的影响，得出整机模态固有频率随零件弹性模量增加而线性增加及相关零件接触面积变化会导致模态不一致的结论。文献[1、6]的研究方法都存在分析样本较少的问题。因此，运用Kriging代理模型进一步研究了接触面积参数不确定对电机模态的影响。

Monte Carlo法、摄动法、快速摄动法等是主要的参数不确定分析方法。这3种方法都是基于研究对象有明确数学表达式来进行参数不确定分析的。然而电机各零件间接触关系复杂，难以建立考虑接触关系的电机动力学模型。文献[7]将电机简化为双环型结构推导了电机的动力学方程，实现了电机动力学模型的构建，但无法分析除定子铁芯和端盖外其他零件间接触面积参数对电机模态的影响。此外，电机有限元模态仿真方法计算量较大，耗时长，采用数据统计分析接触面积参数对电机模态的影响时，其效率低。

基于确定性电机模态仿真模型，采用Kriging代理模型建立了接触面积参数不确定电机模态计算模型；结合Monte Carlo法分析了电机模态对前后端盖螺栓处结合面、定子铁芯与前端盖、前端盖轴承与前端盖等电机接触面积参数的灵敏度。研究结果表明，定子铁芯与前端盖接触面积对电机一、二阶椭圆模态、四阶三角形模态的影响最大，对电机三阶三角形模态影响最大的是爪极与线圈接触面积，同时定子铁芯与绕组接触面积对一阶椭圆模态、三、四阶三角形模态都有影响。研究结果可以为电机模态不一致问题的解决提供依据。

2 接触面积参数不确定电机模态计算的Kriging代理模型建立

采用Kriging代理模型建立接触面积参数不确定的电机模态计算模型，用Kriging代理模型代替复杂的实验、动力学或仿真计算，提高电机模态对接触面积参数的灵敏度分析效率。Kriging代理模型是利用近似方法对离散数据进行拟合的数学模型，包括样本点的选取和预测模型的构建[11]。对于多参数问题正交试验设计法最为合适，故采用正交试验设计法进行样本点选取，它可以以较少的抽样样本获得良好的随机抽样效果。接触面积参数不确定的电机模态计算Kriging代理模型建立主要包括仿真基础模型建立、接触面积参数模型样本采样、Kriging代理模型建立和Kriging代理模型验证4个步骤。

2.1 仿真基础模型的建立

研究对象为汽车用有刷交流发电机，其主要零件包括转子、定子、前、后端盖及其它附件。在构建Kriging代理模型之前，需要建立电机模态采样基础模型。采用ANSYS workbench有限元软件对电机各零件间生产装配过程中的接触关系和接触面积进行仿真，各零件之间所用接触类型为绑定和不分离。电机的模态仿真模型的计算结果，如图1所示。模态仿真与锤击实验结果对比，如表1所示。由表可知，仿真与实验结果之间最大误差为3.5%，说明可以采用该模型进行样本采样构建Kriging代理模型。

图1 电机模态仿真结果Fig.1 Simulation Results of Motor Modal

表1 电机模态仿真结果（单位：Hz）Tab.1 Simulation Results of Motor Modal（Units：Hz）

2.2 接触面积参数不确定电机模态计算的Kriging代理模型建立

电机接触面积参数选定为：a-前后端盖螺栓处结合面接触面积；b-前后端盖止口圆柱面接触面积；c-定子铁芯与前端盖接触面积；d-前端盖轴承与前端盖接触面积；e-后端盖轴承与后端盖接触面积；f-轴承与轴接触面积；g-爪极与轴接触面积；h-爪极与线圈接触面积；i-定子铁芯与绕组接触面积。这些接触面积参数的变化范围均为0～1（数值表示两个零件接触面积占零件接触面总面积的比，0和1分别表示0接触和100%接触，其他数值类推）。运用正交试验设计法选取32个样本，各参数对应样本，如表2所示。

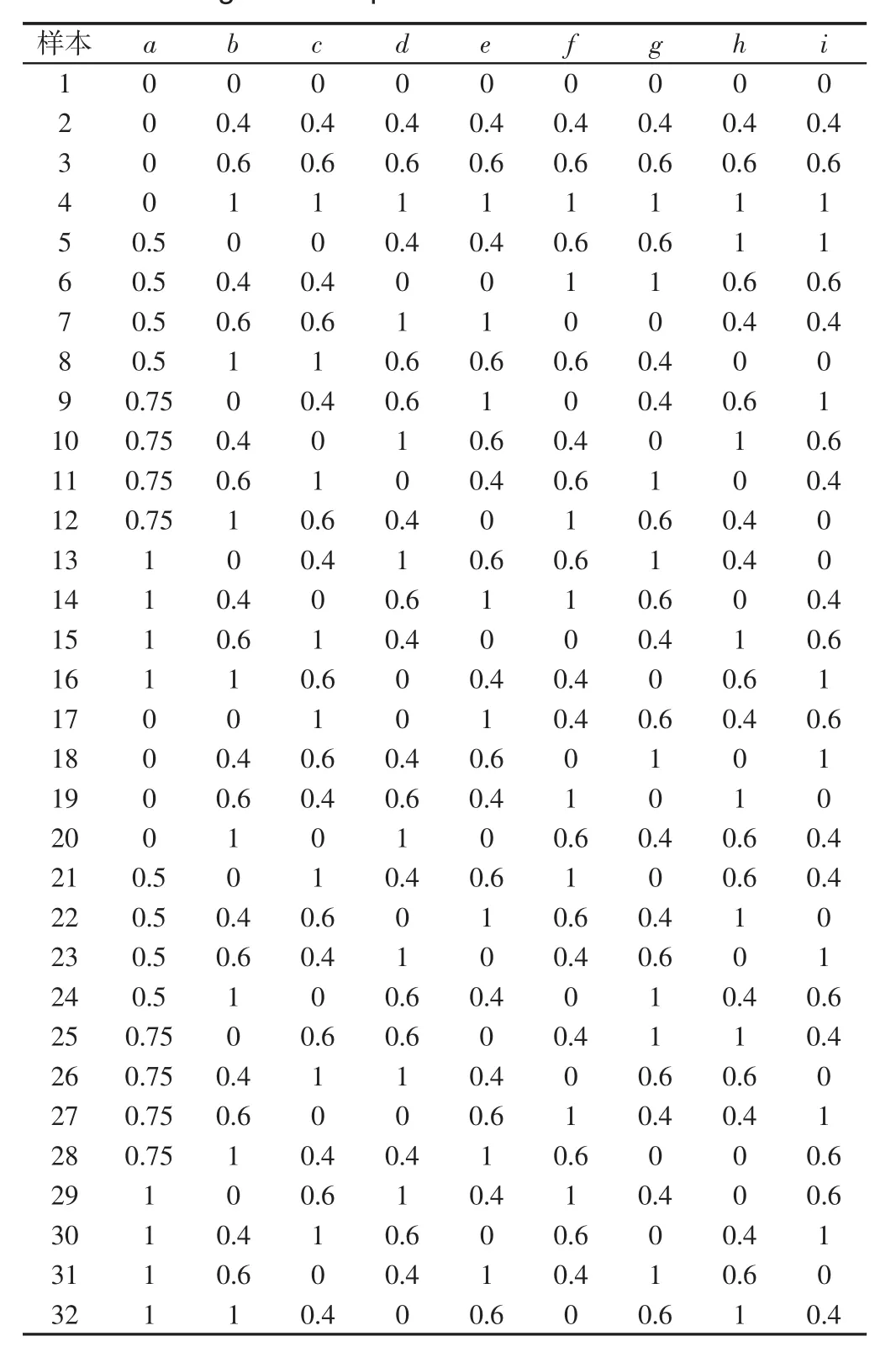
表2 接触面积参数正交样本Tab.2 Orthogonal Samples of Contact Area Parameters

设表2正交试验采集的接触面积参数样本及其对应的模态（此处模态指模态固有频率，下同）为：

接触面积参数及模态固有频率值之间的关系由回归模型F（β，x）与零均值正态分布随机过程ϵ（xi）的和表示：

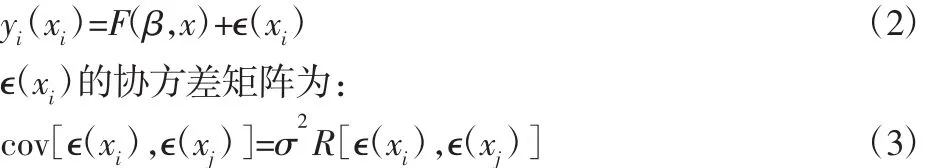
式中：1≤i，j≤n，σ—随机过程的标准差；R［ϵ（xi），ϵ（xj）］—样本 i，j之间的相关函数，此相关函数为Kriging函数。对于一个k

（此处k=9）维变量空间，Kriging函数表示为：

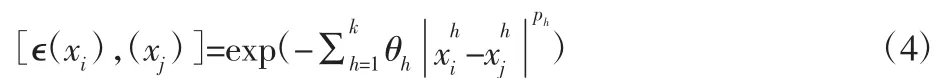
式中：θh—第h个变量对目标的贡献度；ph—表征函数平滑性的参数。建立代理模型要求消除已知样本的建模误差，无偏地反映所有的样本映射关系。能够消除建模误差的可能性的概率密度函数为[11]：

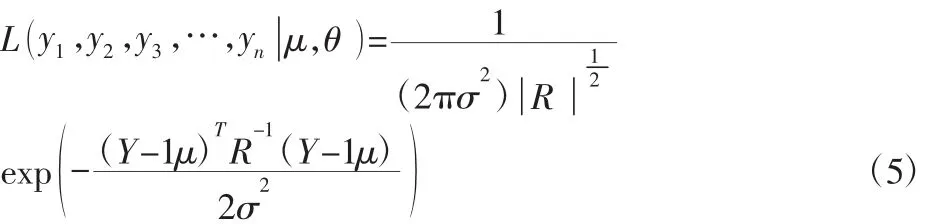
1为元素均为1的n×1阶矩阵，等式两边取自然对数有：

R为所有正交采集样本的相关矩阵：

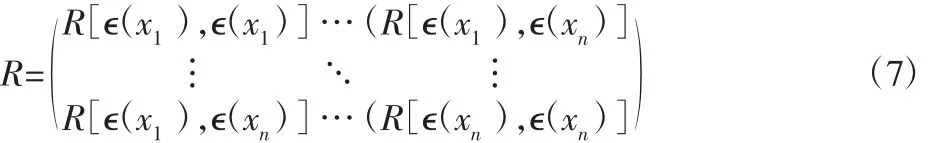
因此，代理模型的建立转化为使得消除建模误差的可能性最大的优化问题。对式（6）中Y与σ2求导，并令其为零，则得到使得可能性最大的μˆ与σˆ：

将式（8）代入式（6），忽略常数项可得：

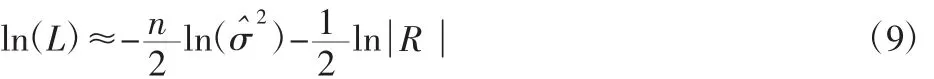
式（9）取值仅与参数θ，p有相关，因此建立代理模型的问题转化为寻找θ，p使得式（9）最大的问题。对式（9）计算其解析最优解，可通过全局优化方法如遗传算法（GA），在一定范围内寻找其数值最优解。

当获得最优的θ，p后，对于不同的接触面积参数x*可通过式（10）预测其对应的模态固有频率值，从而用建立的代理模型代替复杂的实验或大量的仿真计算：

式中：r—待测未知接触面积参数样本x*与初始样本集中各样本点的相关向量：

至此接触面积参数不确定电机模态计算的Kriging代理模型建立完成。

2.3 Kriging代理模型的验证

为了验证所建立的Kriging代理模型的正确性，随机抽取5个样本，运用建立的Kriging代理模型和仿真方法计算验证样本模态，验证样本点，如表3所示。

表3 验证样本Tab.3 Samples for Verification

采用评价系数R2进行验证[8]：

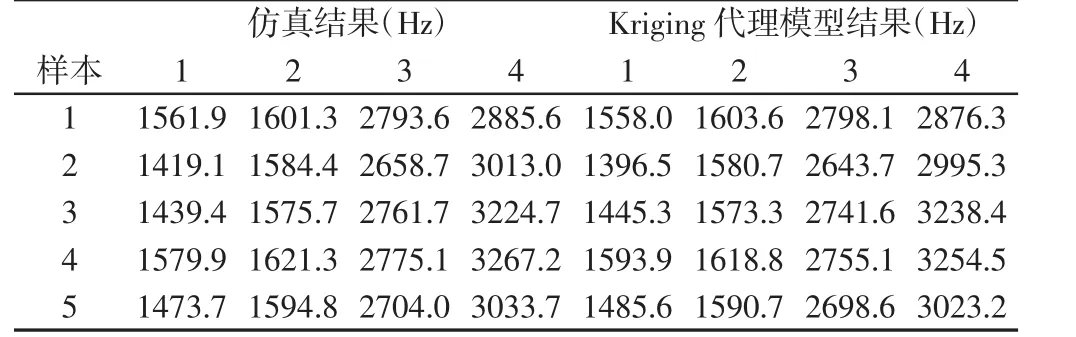
表4 验证样本结果Tab.4 The Results of Samples for Verification

3 基于Kriging代理模型的电机模态对接触面积参数的灵敏度分析

灵敏度S是表征参数对函数值影响程度的重要指标，它是由函数值对参数的导数（一个参数时）或者偏导（多个参数时）得到的[9]。对于电机模态灵敏度的分析可以有效的识别对电机模态影响最大的接触面积参数，为电机模态一致性较差问题的改善提供指导意见。在电机模态对接触面积参数的灵敏度分析中，分析电机模态固有频率均值对接触面积参数均值的灵敏度。电机模态固有频率的均值为，电机各接触面积参数均值为则电机模态固有频率均值对接触面积参数均值的灵敏度计算公式为[10]：

3.1 电机模态对接触面积参数的灵敏度分析

假设各接触面积参数服从正态分布，利用前文中建立的Kriging代理模型结合Monte Carlo法计算电机各阶模态均值，主要分析电机一阶、二阶椭圆模态均值，三阶、四阶三角形模态均值对9个接触面积参数均值的灵敏度。MonteCarlo法模拟计算的次数为106次，且每个参数均值对应的正态分布标准差都相同。计算结果，如图（2）～图（5）所示（此处灵敏度结果表示零件间接触面积均值每增加总接触面积的10%，模态均值就变化对应纵坐标数值）。由图（2）～图（5）可知，定子铁芯与前端盖接触面积对电机一、二椭圆模态、四阶三角形模态影响最大，对电机三阶三角形模态影响最大的是爪极与线圈接触面积，同时定子铁芯与绕组接触面积对电机一阶椭圆模态、三、四阶三角形模态都有较大影响，如表5所示。这一研究结果可以为电机模态不一致问题的改善提供依据。

图2 一阶椭圆模态接触面积参数灵敏度Fig.2 Sensitivity Results of the1st Order Elliptic Modal for the Contact Area Parameters

图3 二阶椭圆模态接触面积参数灵敏度Fig.3 Sensitivity Results of the 2nd Order Elliptic Modal for the Contact Area Parameters

图4 三阶三角形模态接触面积参数灵敏度Fig.4 Sensitivity Results of the 3nd Order Triquetrous Modal for the Contact Area Parameters

图5 四阶三角形模态接触面积参数灵敏度Fig.5 Sensitivity Results of 4th Order Triquetrous Modal for the Contact Area Parameters

表5 各阶模态对接触面积参数的灵敏度结果Tab.5 Sensitivity Results of Every Order Modal for the Contact Area Parameters

4 结论

研究了接触面积参数不确定对电机模态的影响。通过电机模态仿真基础模型建立、Kriging代理模型样本采样、Kriging代理模型构建，建立了接触面积参数不确定电机模态计算的Kriging代理模型，并结合Monte Carlo法对电机模态进行接触面积参数的灵敏度分析，主要结论如下：（1）建立并验证了接触面积参数不确定电机模态计算的Kriging代理模型，运用这一模型计算了接触面积参数不确定电机的模态。接触面积参数不确定电机模态计算的Kriging代理模型不需要推导复杂的电机动力学方程，用它代替模态测试实验和模态仿真计算，提高了研究效率和准确性。（2）基于Kriging代理模型结合MonteCarlo法分析了电机模态对接触面积参数的灵敏度，得出了定子铁芯与前端盖接触面积对电机一、二阶椭圆模态、四阶三角形模态影响最大，对电机三阶三角形模态影响最大的是爪极与线圈接触面积，同时定子铁芯与绕组接触面积对电机一阶椭圆模态、三、四阶三角形模态都有较大影响的结论。（3）研究结果可以为电机模态不一致问题的解决提供依据。