关于乘法分配律的几点慎思与求索
2020-06-19徐小琴
徐小琴
摘 要 乘法分配律是小学数学的重要内容,也是备受争议的教学难点与易错内容。通过对乘法分配律“应该如何教学”“字母表示是否科学”“教学价值何在”的思考,提出乘法分配律教学应重数学本质、定律字母的表示应凸显地位与顺序、乘法分配律教学应贯穿联系整个知识体系的理念。
关键词 乘法分配律 教学 慎思 求索
乘法分配律是小学四年级乘法运算定律的重要内容,是乘法交换律和结合律之后的一个基本运算定律。本节内容是各种公开课、示范课的热门课例,也是一线教师公认的“难啃的骨头”。因此,基于已有文献研究及乘法分配律内容结构的横纵联系,笔者拟从理解数学本质的角度谈一些看法。
一、乘法分配律应该如何教
1.已有教学重情境轻本质
情境教学开创了教学改革的新天地,数学课堂引入情境使原本静态的知识充满生命。关于乘法分配律的教学情境包括:计算课桌椅的价格[1]、计算套装衣服的价格、计算等宽异长的长方形(菜园)的面积[2]、计算参加植树活动的学生人数[3]等形式。其教学设计过程都体现了从情境出发提炼不同算式,通过分组或者比赛的形式计算数值,比较计算方式,将更为简单的计算方法抽象出符号表达式,让学生经历现实情境数学化、数学知识符号化的过程。
但是,教学最经济的方式是“同化”。无论上述情境以何种方式教学,学习此内容学生能联系到的已有知识基础就是乘法与加法的运算,尽管有经历知识建构的过程,但对乘法分配律的原理是以一个新知识、新内容进行顺应的,离不开教师的“精心设计”。那么,乘法分配律本身有没有脱离现实背景的数学意义呢?其实,乘法分配律并不是一个新知识,而是学生已有的知识经验。
2.乘法分配律教学应重视数学本质
通常情况下独立的知识内容学生掌握较好,但遇到新的问题情境或须要综合几个知識内容解决问题时就捉襟见肘、相形见绌。教学是由一个问题情境讲一个知识内容的循环往复。挖掘学生已有知识经验,建立新旧知识间的脚手架,达到学生认知最近发展区,才能实现教学的部分之和大于整体的成效。用数学知识串联数学知识,建立数学知识的实质性联系,一堂充溢数学味的课才是数学教学的真谛。
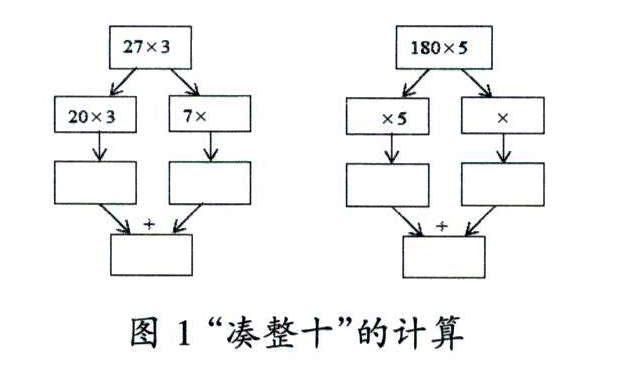
纵观乘法分配律的前提铺垫,在三年级下册两位数乘两位数的口算乘法中就已经初步建立起“分配”原则的意识,只是侧重于“凑整十”的计算,如图1[4]所示。
这是两位数乘一位数的乘法应用,其中学生已经初步具备将27拆分为20和7的理念(凑整)。27乘以3就是27个3,也就是20个3加7个3,180乘以5也就同理可得。其中提示被乘数可拆分为两组数的和,并且是“几个3与几个3的和是27个3,几个5与几个5的和是180个5”。这就是早期建立起的乘法分配律的知识基础,也是乘法分配律的脚手架——一个数与两个数的和相乘。只是,这两个数中有一个为整十数,是符合小学低段学生认知水平的。
两位数与两位数的乘法计算中,竖式计算是乘法计算的重要计算方式,在竖式计算教学中,渗透乘法分配律,如图2[5]所示。
此竖式计算中,14与12相乘,分别用乘数中个位的2、十位的1与被乘数14相乘,结果相加。此过程充分体现了乘法分配律的原则,其模型构建过程如图3所示。
因此,乘法分配律对四年级学生来说并不是一个陌生的新问题,而是熟悉的旧知识,教学过程只需要唤起学生对已有知识的再现,使学生认识“知识的来源”,用“乘法分配律”赋予知识新的命名。
乘法分配律的教学应直接以“ 怎么计算”为问题切入口,去除非本质的生活情境,在乘法竖式计算的过程中剖析计算过程的法与理(算法与算理)。同时,以此为基准认识12可以任由两个数的和组成,破除已有知识的桎梏,导之以数学问题,得到结构化的知识框架,并举例应用。
二、乘法分配律的字母表示科学吗
教材[6]乘法分配律的字母表示为(a+b)×c=a×c+b×c ,这是乘法左分配律,表达式看似简单易懂,是字母表示数的典型代表,也是培养学生符号意识和抽象素养的基础。但是,教材乘法分配律的字母表示存在字母间地位不凸显的问题,学生易产生字母间的混淆,这也是学生容易出错的地方。同时,在介绍左分配律和右分配律的顺序上有失稳妥,对后继学习的迁移也有影响。
1.字母地位不凸显,学生易混淆
字母表示数,26个英文字母的地位与作用看似一样,但事实上不同的字母在数学学科中有着其约定俗成的意义,如面积用S,边长用a,高用h,未知数通常用 x,y来表示等。除了考虑部分英文字母首字母以外,更应符合学生的认知规律。
乘法分配律中的字母选择的是学生最熟悉的连续字母 ,三者之间的关系犹如姊妹、兄弟。从心理学的角度来看,其共同属性较多,区分度较低,学生在应用过程中容易产生概念泛化。因此,可将乘法分配律的字母表达式改为(a+b)×m=a×m+b×m。字母a,b的关系依旧是姊妹、兄弟,而m与a,b区分度高,学生理解更容易。该形式更具有推广价值,如(a+b+c)×m=a×m+b×m+c×m等。
2.左右分配顺序颠倒,学生难迁移
大多数教师的教学与教材设置一样,将教学重点落在左分配律的学习上,最后通过“想一想”“试一试”等问题设计验证右分配律的存在,并且根据乘法的交换律得出左、右分配律的结果相等。通过后续学习我们知道,左分配律和右分配律在大多情况下是不相等的,如向量,矩阵。那么,左、右分配律哪一个更重要呢?右分配律更重要。杜威认为,思维的开始阶段就是经验[7]。也就是思维产生于学生已经知道的或者积累的认识事物的一般规律。人类认识事物的一般规律是由易到难,由特殊到一般。乘法右分配律m×(a+b)=m×a+m×b表示一个数与两个数的和相乘,等于这个数分别与两个数分别相乘,再相加。m在运算过程中不变,分配过程相当于 穿透括号分别与a,b作用,也将“分配”具体化。因此,右分配律更符合学生认知规律,具有科学性。
从学习知识的迁移角度来看,右分配律对后继学习简便计算、提取公因数(公因式)、提取公因式等有重要铺垫作用。因此,乘法右分配律具有重要的迁移价值,应作为教学重点。
三、乘法分配律的价值何在
1.乘法分配律为小学简便计算提供方法
小学四年级的一个重要内容就是乘法运算定律的学习,而运算定律学习的一个共同目标就是简便计算,初步培养学生的发散思维。乘法分配律的学习为复杂的混合运算提供方法基础,如计算111×7+3×111,运用乘法分配律的逆运算能简化运算量,在审题、读题过程中发现数与数的关系,再现知识储备中的计算方法,对学生思维的培养(逆向、发散思维等)具有一定作用。
2.乘法分配律为初中因式分解提供指导
因式分解在数的简便计算、整式的除法、分式的混合运算、解方程等方面都具有潜在的重要作用[8]。进行因式分解的重要方法就是提取公因式,找出多项式中的公因式也就成为了教学的重难点。与提取公因式密切联系的知识基础就是乘法分配律,简单的说提取公因式就是乘法分配律的逆运算,即提取多项式中都含有的相同因式。因此,乘法分配律的学习对后继学习因式分解具有积极作用。
3.乘法分配律为高等数学学习提供原理
乘法分配律在高等数学的众多知识内容中仍就存在,数与矩阵的和满足分配律,矩阵的乘法和加法满足分配律,这都是矩阵问题中常用的性质,也是推导其它性质的基础。同时,乘法分配律为群论、拓扑学、复变、泛函等高等数学学习都提供了指导性原理。
可见,乘法分配律具有重要的教学价值和理论意义。在小学数学教学中渗透其教育价值有利于学生知晓“知识的去向”,对培养学生的学科素养和科学精神具有现实意义。
参考文献
[1] 许万明.乘法分配律教学探新[J].小学教学研究,1994(11).
[2] 徐伟平.借助几何直观,提高运算教学效率[J].教学与管理:小学版,2015(20).
[3] 丁玉华.以问题提出促进意义构建——“乘法分配律”教与学现状分析及教學建议[J].教育科学论坛,2019(04).
[4] 曹才翰,章建跃.数学教育心理学[M].第2版.北京:北京师范大学出版社,2006.
[5] 人民教育出版社课程教材研究所.义务教育教科书数学三年级(下册)[M].北京:人民教育出版社,2014.
[6] 人民教育出版社课程教材研究所.义务教育教科书数学四年级(下册)[M].北京:人民教育出版社,2014.
[7] 杜威.民主主义与教育[M].王承绪,译.北京:人民教育出版社,2001.
[8] 金晓群.重视数学学习中必要性的体验[J].教学与管理,2007(31).
[责任编辑:陈国庆]
该文为四川省“西部卓越中学数学教师协同培养计划”项目(ZY16001)、2018年度内江师范学院科研项目“基于PME视角的数学建模素养实践路径的探索”(18SC11)的阶段性研究成果
