一种计算底水油藏水锥形态与见水时间的新方法

杜殿发 张彬 夏曦 黄时祯 吴震

1. 中国石油大学(华东)非常规油气开发教育部重点实验室；2. 中国石油大学(华东)石油工程学院；3. 中国石油天然气股份有限公司塔里木油田分公司

底水油藏开发不可避免遇到底水锥进问题，油井见水后产量下降，影响油藏开发效率[1-3]。研究底水锥进问题的关键在于确定油井生产时地层垂向压差与水锥重力势能的平衡关系，所以就需要准确地描述底水锥进过程中储层压力的变化。李传亮[4-5]提出的Dupuit公式假设底水油藏的流态为平面径向流，并认为径向压差近似等于垂向压差，该方法对于部分射开井忽略了球形流动状态。因此一些学者采用不同的流态描述底水油藏的锥进问题，如球面向心流[6]、平面径向流[7]、半球面向心流相结合[8-9]等,但此类模型对于厚油藏与部分射开井均未考虑球面向心流与平面径向流的过渡过程。涂彬[10]、谷建伟[11]、蒋平[12]虽然考虑了油藏实际流态的过渡特征，但未考虑实际地层压力分布特征。上述模型均假设油水界面至井底的压力分布为线性变化，忽略了实际油井生产时地层压降集中于井底附近的实际情况，因此假设压力分布为线性变化计算底水锥进问题存在不足。综上所述，对于目前各方法存在的不合理性，针对部分射开油井考虑实际地层变压力梯度分布建立数学模型，并采用数值反演准确计算地层压力分布规律，研究水锥形态及影响因素，为底水油藏开发提供理论依据。

1 部分射开井理论模型建立

实际生产中许多油井射孔生产层位于油藏中部，油井生产状态不再是简单的射孔段平面径向流、射孔段下部半球状向心流。因此基于基本渗流微分方程建立底水油藏中部的部分射开井数学模型，并采用Stehfest数值反演及分离变量法对所建模型的拉普拉斯变换式进行求解，得到真实的地层压力分布；进而研究油井在任意产量下生产时水锥的变化形态和油井见水时间等问题。

1.1 物理模型

部分射开井开发底水油藏模型如图1所示，基本假设为：忽略重力、毛管力；开井生产前地层压力均匀分布为pi；流体流动满足达西定律；油藏等厚无限大，顶边界为封闭边界，底边界为底水定压边界；油井只射开Zb−Za厚度，以定产量q生产；地层垂向和水平渗透率分别为Kv、Kh。其中，Za为油层上部未射开段厚度，m；Zb为射开段至油层顶的距离，m；h为储层有效厚度，m；q为油井产量，m3/s；Kv为地层垂向渗透率，10−3μm2；Kh为地层水平渗透率，10−3μm2。

图1 假设部分射开井地层示意图Fig. 1 Schematic formation in assumed perforated wells

1.2 数学模型

定义如下无因次变量为

式中，pD为无因次压力；pi为地层原始压力，MPa；p为储层某一点的压力，MPa；μ为原油黏度，mPa · s；B为原油体积系数；tD为无因次生产时间；t为生产时间，s；ϕ为孔隙度，小数；Ct为综合压缩系数，MPa−1；rw为井筒半径，m；CD为无因次井筒储集系数；C为井筒储集系数；rD为无因次半径；r为储层某点距井筒水平距离，m；ZD为无因次射孔高度；Z为射孔高度，m；hD为无因次储层厚度；LD为无因次射孔厚度。

由无因次变量定义以及基本假设，可以得到底水油藏部分射开井无因次数学渗流模型［13］，综合渗流微分方程为

初始条件为

顶部封闭边界为

底部定压边界(底水定压边界)为

外边界条件为

内边界条件为

式中，ZaD为射孔顶处无因次高度；ZbD为射孔底处无因次高度。

2 模型求解

对以上数学模型进行Laplace变换，并采用分离变量法进行求解，可以得到Laplace空间中底水油藏部分射开井的压力分布情况为

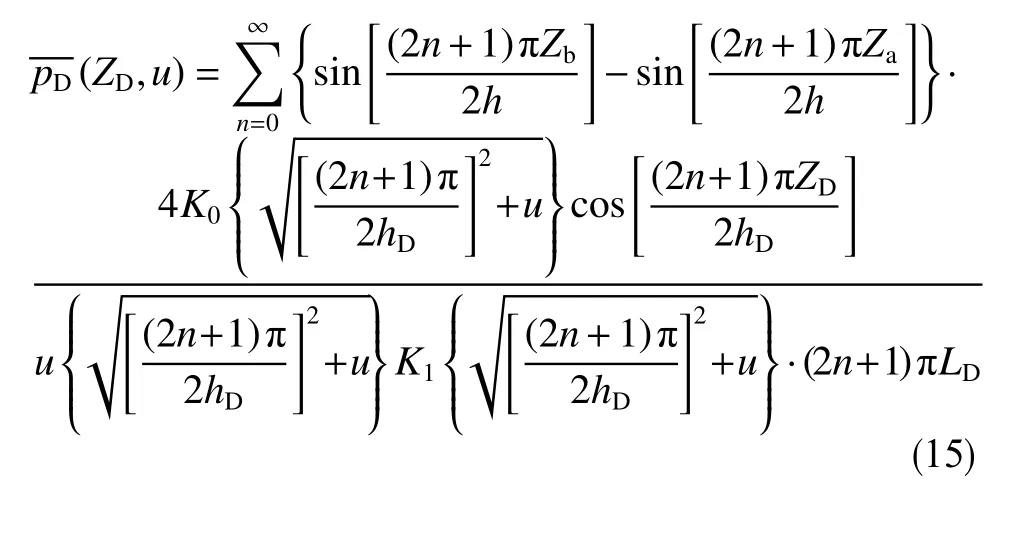
最后采用Stehfest数值反演得到真实空间下底水油藏部分射开井的压力动态。

1.2.3 与物理方法复合使用 研究发现，拮抗菌复合热处理、紫外处理在柑橘青霉病和桃果实软腐病等多种果蔬病害生物防治中效果显著[1]。例如，Xu等[23]发现，Candida guilliermondii和UV-C复合使用能够有效控制梨果实采后青霉和灰霉的发生，而拮抗菌的生长并不受UV-C的影响。此外，复合处理诱导提高了梨果实几丁质酶、β-1,3-葡聚糖酶、过氧化氢酶和过氧化物酶的活性。Alvindia等[24]将Trichoderma harzianum DGA01和热水处理复合来防治香蕉冠腐病，显著降低了香蕉冠腐病发病率，并且香蕉的果实品质也明显高于杀菌剂浸泡处理组。

3 水锥参数计算

3.1 生产动态压力分析

上述模型得到部分射开井的井底压差变化分为3个阶段，在第3阶段压差趋于稳定。由于井底压差达到稳定前的生产时间占整个生产过程的比重非常小，为方便计算和分析，将采用井底压差达到稳定后的结果进行相关参数计算。为了更直观地分析地层流体的渗流场，绘制底水油藏的等压线(图2)。

图2 部分射开井地层等压线图Fig. 2 Isobaric contour map of the formations in some perforated wells

由水动力学可知，地层任一点的瞬时速度矢量都与等压线正交，则由图2可判断部分射开井生产时地层流体的运动轨迹。并由图2可知以井底为平面可将地层的流动划分为上下两部分：上半部分以径向流动为主，而下半部分以垂向流动为主。通过等压线的密集程度可看出，主要压力降分布于井筒周围，离井筒距离越近，压降速度越快，流体运动速度越快。同时上半部分等压线随着半径的增大逐渐变得稀疏，说明随着半径的增大，地层流体的运动速度减慢，即远井地带的储量难以动用，使得底水油藏的采收率远低于常规边水或人工水驱油藏；而下半部分等压线随着半径的增大也逐渐变得稀疏，垂向压力梯度呈递减趋势，所以相同时间内流体垂向的运行距离随半径的增大而减小，形成水锥。

计算井底至油水界面各点垂向压力梯度变化规律如图3所示。

图3 井底至油水界面各点垂向压力导数Fig. 3 Derivative of each vertical pressure from the bottom hole to the oil-water contact

常规解析公式的见水时间计算方法是通过线性的压力梯度来计算水质点的驱动压差，但由图3可知，实际开发中垂向压力梯度并不是线性而是类似“L”形分布，这表明主要压力降在距离井底附近区域，油水界面处垂向压力梯度低，底水向上锥进动力弱，因此底水锥进速度慢、见水时间大、无水采油期长。如果使用简单的线性分布计算，油水界面处垂向压力梯度相对较高，底水上升较快，使得无水采油期较短。另外，根据该垂向压力梯度分布可知在理论上不存在临界产量，因为使水锥稳定在某处的前提条件是该点垂向压力梯度的值为(ρw−ρo)g（ρw为地层水密度，kg/m3；ρo储层原油密度，kg/m3）［14］。如果按照常规分析方法将判断点选在井底并以此计算临界产量的话，那么在油水界面处的压力梯度将远小于井底的压力梯度，即油水界面的压力梯度远小于(ρw−ρo)g，这样底水将不会继续向上锥进，同样如果选择油水界面附近为参考点，那么井底处的压力梯度会远大于(ρw−ρo)g，则水锥仍不能稳定。

3.2 见水时间的计算

由达西渗流定律可知地层任一点向上的渗流速度为

式中，p为地层任一点处的压差，MPa。

改写为

由定压边界向井底积分可以得到水质点在定产量下到达井底的时间为

式中，Δp'为任意高度处距井底压差，MPa；Δρ为油水密度差，kg/m3。

通过上述公式可求得井底至油水界面各点垂向压力梯度如图2所示。将该压力梯度带入公式(19)可求得目标井见水时间。

3.3 水锥形态

水质点由油水界面垂向运动到Z1处所需的时间为

将已求得任意半径r处垂向压力梯度代入上式

即可求得t1时刻任意半径r处的水锥高度Zn。通过计算目标井下部底水锥进至井筒垂向的不同位置的时间，可计算出在不同时间下不同半径处各点水锥高度。

3.4 见水时间和水锥形态的影响因素

(1)产量。经过计算发现随着产量的减小，油井见水时间延长，井底水锥的锥体两侧更“窄”，整个锥体更“尖”，这种趋势在油井产量较小时的变化最为明显，随着产量进一步提高整个锥体变化并不明显。无水采油量随油井产量的提高而减小，但显著递减同样发生在产量较小时。这是因为当油井产量较小时，地层垂向梯度受(ρw−ρo)g影响明显，垂向供油量变化占比总供油量变化较大，但当产量较大时(ρw−ρo)g影响较小，随着径向供油量提升，垂向供油量的变化对总供油量变化影响减弱。不同产量下油井见水时的水锥形态如图4所示。

(2)垂向渗透率。如图5所示，随着地层各向异性比Kh/Kv增大，地层非均质性越强，垂向渗透率越小，相同产量下底水锥进速度越慢，水锥锥体越小，无水采油期越长，无水采油量也就越大。

3.5 实例验证

目标区块原始地层压力50.63 MPa，经过近20年的开发，目前实测地层压力47.65 MPa，压力保持程度94.1%，为天然能量充足油藏，符合模型假设条件。物性资料：日产量为76 m3/d，原油体积系数为1.12，径向渗透率为0.415 μm2，垂向渗透率为41.5×10−3μm2，孔隙度为20%，无水采油期为125 d，油层厚度为19.5 m，射开厚度为10 m，静压为50.34 MPa，流压为49.24 MPa，避水高度为9.5 m，原油黏度为4.18 mPa · s；原油密度为830 kg/m3。

图4 不同产量下油井见水时的水锥形态Fig. 4 Breakthrough water cone shape at different yields

图5 不同地层各向异性比下油井见水时的水锥形态Fig. 5 Breakthrough water cone shape at different formation anisotropy ratios

经过模型计算目标井见水时间为110 d，与实际无水采油期125 d较为接近，但如果以常规底水油藏解析公式计算见水时间为30 d左右，因为常规解析公式的见水时间计算方法是通过线性的压力梯度来计算水质点的驱动压差，这就使见水时间计算结果要低于实际值。目标井底水锥形态变化如图6所示。

图6 目标井水锥形态变化Fig. 6 Change of water cone shape of the target well

4 结论

(1)基于部分射开井的压力动态给出了一种计算油井见水时间和水锥形态的新方法，该方法可以更加准确地描述底水油藏开发的压力动态和底水锥进情况。

(2)通过分析底水油藏油井生产时的垂向压力梯度分布发现：底水油藏开发过程中垂向压力梯度并不是线性分布而是类似“L”形分布，即主要压力降在离井底较近的地方，如果基于常规方法中假设压力梯度为定值的方法计算见水时间，其结果偏小。

(3)基于理论模型分析了产量和垂向渗透率对底水锥进的影响，结果表明：随着产量的减小，油井见水时间延长，井底水锥的锥体两侧更“窄”，整个锥体更“尖”，该趋势在油井产量较小时的变化最为明显；而随着垂向渗透率的增大，水锥锥体也不断增大，无水采油期越短。