广义回归估计量在中国农业抽样调查中的应用研究
2020-06-18杨贵军沈文静
杨贵军,沈文静
(天津财经大学 a.统计学院;b.中国经济统计研究中心,天津 300222)
一、引言
准确掌握非普查年农业生产经营活动情况有助于政府及时把握“三农”问题,为科学制定“三农”政策、进行宏观经济管理与调控提供必要的数据支持。目前,有关中国非普查年农业生产经营活动情况的估计主要依赖于农业抽样调查,如农作物面积遥感测量和对地抽样调查、农作物单位面积产量抽样调查以及主要畜禽抽样调查。估计量设计是决定抽样估计精度的关键。因此,如何改进估计量,提高估计精度,是各国政府农业统计工作及本文的聚焦点。
中国农业抽样调查主要采用赫维茨—汤普森估计量(HT估计量)。HT估计量对总体总值估计的基本思想为:将每个样本单元的观测值自加权1/πk倍再求和,其中πk为第k个样本单元的入样概率。尽管HT估计量具有无偏性,但在实践中仍具有一定局限性,即仅利用样本观测值和入样概率进行总体参数估计,而未使用任何辅助信息。中国每十年开展一次全国农业普查,动用了大量人力、物力和财力,收集了最为全面、准确和丰富的农业数据资料。此外,农业数据资料还包括历史抽样调查数据、农业行政记录、遥感数据和以空前速度增长的由智能农业机械收集的实地观察数据。采用HT估计量容易造成农业数据资料不充分利用,不能保证对农业生产经营活动指标估计的精度,特别是在样本代表性不足的情况下,很可能导致严重的误差。
一种能有效利用辅助信息且具有代表性的估计量为广义回归估计量。广义回归估计量最早由Cassel等人提出并系统研究,以调查变量和辅助变量构建的超总体线性回归模型为基础[1]。当辅助变量总体总值和样本辅助变量值可获得时,依据调查变量与辅助变量的回归关系,估计模型回归系数,从而构造总体参数的广义回归估计量。概括来看,采用广义回归估计量估计农业生产经营活动情况的优势主要包括三个方面:一是统计性质的优良性。广义回归估计量不仅具有渐近设计无偏性,当假定的超总体线性回归模型能够很好地拟合总体数据,且样本规模相同时,广义回归估计量通常比HT估计量的方差更小[2]。二是广义回归估计量能够更充分地利用辅助信息。其利用任何已知总体总值和样本单元值的辅助信息,大多数利用辅助信息的估计量均可看做广义回归估计量的特殊情况,如比率估计量、简单回归估计量和事后分层估计量等[3]。三是广义回归估计量具有广泛的扩展性,能适用于任何抽样设计,如分层抽样、整群抽样、多阶段抽样、两步抽样和连续抽样等[4]。
另一方面,诸多国家的政府统计部门已在实践中采用广义回归估计量。例如,美国统计局于1997年开始在农业抽样调查中推广使用多变量与规模成比例的概率抽样和广义回归估计量,替代原来的分层抽样和HT估计量[5]。加拿大统计局已构建了以广义回归估计量为核心的广义估计系统,并逐步应用于普查、商业调查、劳动力调查和多项追踪调查[6]。澳大利亚统计局则主要将广义回归估计量应用于商业调查[7]。尽管中国政府统计部门还未将广义回归估计量应用于实践调查,但已有学者对广义回归估计量进行了系统的研究。其中,陈光慧基于连续二阶抽样方案,给出了中国农产量调查中构造广义回归估计量的具体步骤[4]。
然而,尚未发现有学者针对中国农业抽样调查,开展广义回归估计量的可行性和适用性研究。这里的可行性是指在当前中国背景下能否获取可用于构造广义回归估计量的辅助信息。适用性主要体现在两个方面,一是当采用广义回归估计量时,能否构建具有实践可操作性的方差估计量,用于衡量广义回归估计量的估计精度,评估农业生产经营活动指标估计值能否使用及在多大程度上使用。二是针对农业抽样调查抽取样本时的特殊情况,如抽样比不同,辅助变量与调查变量的相关性不同,广义回归估计量相比于HT估计量是否能保持统计性质上的优势。
鉴于此,本文的研究目标为评估在中国农业抽样调查中,构建广义回归估计量替代现行HT估计量的可行性及适用性。研究意义体现在三方面:一是广义回归估计量的统计性质更优良,显著提高对中国农业生产经营活动情况的估计精度;二是有助于中国国家统计局进一步推广应用广义回归估计量,为未来中国农业抽样调查方案设计提供指导;三是对中国农业抽样调查中广义回归估计量构造方法的研究,有助于提升中国在农业抽样调查领域的基础理论水平。
二、广义回归估计量的构造
(一)辅助信息的选择
鉴于在中国农业抽样调查中使用广义回归估计量的基本前提是辅助信息的可获得性、真实性和完整性,本文首先讨论中国背景下可利用的辅助信息。目前,可用于中国农业抽样调查的辅助信息有很多。其中,农业普查数据为后续农业抽样调查提供了最为全面、准确和丰富的辅助信息资料。农业行政记录是指能够用来生产农业统计(即农业经济统计、农业社会统计和农业环境统计)的行政记录,由政府部门和其他组织为行政(非统计)目的而收集,通常是在提供服务期间或为登记、保存记录或记录交易而收集的信息。由于其收集频率高、承载信息的单位小且成本相对较低,成为农业政府统计亟待开发使用的重要信息资源。遥感数据主要分为两种,即航天遥感数据和航空遥感数据。遥感数据不仅能提供田间的空间覆盖,还可以每天生成有关植物健康、当地天气和作物条件的读数,得到作物生产的实时估算。将遥感技术与现场观测相结合,已成为估计农作物种植面积的重要途径。智能农业机械化的快速发展,也使收集农作物投入和产出的现场数据成为可能。
表1列举了部分可用于广义回归估计量的辅助信息及具体用途。此外,为保证辅助信息所提供的总体辅助变量总值和样本单元辅助变量值的真实性,以及对样本单元较高的覆盖度,有必要对辅助信息进行数据质量评估和整合[8]。技术细节请参见孟杰等人的研究以及世界粮农组织的系列工作文件[9-10]。

表1 构造广义回归估计量的辅助信息
(二)广义回归估计量
分层两阶段抽样是中国农业抽样调查的重要抽样方法,如普查年和非普查年的农作物面积遥感测量和对地抽样调查、非普查年的主要畜禽抽样调查。对于第一阶段抽样,通常以行政村为初级抽样单元,采用与单元大小成比例的概率抽样方法抽选村。鉴于不放回抽样比有放回抽样的效率更高,本文讨论基于不放回的与单元大小成比例的概率抽样,即πPS抽样。对于第二阶段抽样,根据实际调查需要,以网格(200米×200米)或养殖场(户)为次级抽样单元,采用的抽样方法为简单随机抽样或随机等距抽样。本文在上述抽样方法下,讨论广义回归估计量在中国农业抽样调查中的构造方法。

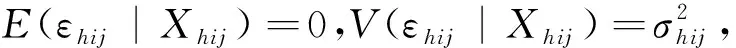
(1)
其中:

(2)


(三)广义回归估计量的方差估计
国内学者对广义回归估计量的方差估计普遍采用基于泰勒级数法的估计量,即:

(3)
其中:

该方差估计量的局限性在于需要为每一个调查变量,分别计算所有样本单元的残差值ehij。若农业抽样调查的变量很多,且样本规模较大,计算过程相当繁琐耗时。此外,对于一阶段为不放回的πPS抽样,πhi,hi′难以计算。因此,式(3)并不适用于实践抽样调查。



2.计算第h层调查变量总值估计的刀切复制值:
(5)

4.第h层调查变量总值广义回归估计量的方差估计量为:
(6)
三、广义回归估计量性质的模拟分析
根据上述理论框架,采用蒙特卡洛模拟方法讨论广义回归估计量在中国农业抽样调查中的统计性质。中国于2016年开展第三次全国农业普查,本文基于第三次全国农业普查结果进行仿真研究,评估广义回归估计量在不同抽样设计下的估计效率。鉴于畜牧业在农业农村经济发展中的重要位置,本文选取中国主要畜禽抽样调查中的牛羊禽监测调查为研究对象。
资料显示,牛羊禽监测调查的主要目标是估计全国牛羊禽散养户的饲养情况,如分品种的存栏量、出栏量和饲养户数等。原则上各省仅在现有国家抽样调查县内开展调查,若存在集中连片牛羊牧区,可将牛羊牧区县划作一个独立设计层进行抽样。每一层内采用二阶段抽样方法,第一阶段是与规模成比例的概率抽样方法抽选行政村;第二阶段从样本村内采用随机等距抽样方法抽取养殖场(户)。考虑到国家抽样调查县30多年不变,对农村总体的代表性大大降低,本模拟假设各省在所有县内开展调查[12]。
将感兴趣的总体参数设定为全省在抽样调查时点的牛羊禽存栏量。选取的辅助信息为养殖场(户)在第三次全国农业普查中的登记结果。三个研究目标为:第一,以牛羊禽养殖场(户)在普查中存栏量的登记结果作为辅助信息,分别构造全省在抽样调查时点牛羊禽存栏量的广义回归估计量,并比较广义回归估计量与HT估计量的估计效果;第二,研究辅助变量与调查变量相关性对广义回归估计量估计效果的影响;第三,研究抽样比,即样本量对广义回归估计量估计效果的影响。
为此,参数设定如下:设全省有400个行政村,每个行政村约25个养殖场(户),普查时共计10 000个养殖场(户)。从普查结果中随机抽取10 000个经脱敏处理的牛羊禽养殖场(户),将其牛羊禽存栏量依次作为模拟中每个养殖场(户)的辅助变量值xk,hij。k=1,2,3分别表示牛、羊和禽。由于缺少集中连片牛羊牧区信息,将所有行政村按养殖规模划分为H=2层,各层的行政村数量分别为240和160。假设在抽样调查时点,各养殖场(户)饲养品种保持不变,且存栏量真实值yk,hij=max{1,|xk,hij+εk,h|},εk,h服从均值为0,标准差为sdk,h/a的正态分布。sdk,h表示第h层饲养第k种畜禽的养殖场(户)在普查中登记存栏量的标准差。调整参数a,使各层内对于每一种畜禽,养殖场(户)的真实存栏量与辅助变量的Pearson相关系数约为ρ,讨论ρ分别为0.85、0.90、0.95和0.99的四种情形。相关总体信息见表2,其中Yk,h和Xk,h分别表示第h层养殖场(户)对第k种畜禽的真实存栏量和辅助变量总值。抽样比分别设定为f1h=0.1,0.3和f2hi=0.1,0.3。估计全省每种畜禽存栏量所用的辅助向量均为Xhij=(1,x1,hij,x2,hij,x3,hij),chij取为1。

表2 总体信息 单位:头/只

(7)
(8)
其中,Yk表示全省在抽样调查时点对第k种畜禽存栏量的真实值。同时,为了验证广义回归估计量在统计性质方面的优势,将其与中国农业抽样调查目前所采用的HT估计量进行对比。全省在抽样调查时点牛、羊和禽存栏量的HT估计量为:
(9)
由表3的模拟结果得到如下三点结论:第一,在估计全省每种畜禽存栏量时,若同时使用养殖场(户)在普查时对三种畜禽存栏量的登记结果作为辅助信息,来构造广义回归估计量,偏差可以忽略不计,可以实现比HT估计量显著减少的相对均方根误差;第二,辅助变量与调查变量的相关性越强,广义回归估计量在统计性质上的优势越明显;第三,随着一阶抽样比或二阶抽样比的增加,即样本量的增多,广义回归估计量的相对均方根误差呈下降趋势。

表3 两种估计量的模拟比较结果
四、广义回归估计量的应用研究
本文在模拟试验的基础上,以ρ=0.99,抽样比f1h=0.1和f2hi=0.1为例,构造全省牛羊禽存栏量的广义回归估计量及其方差估计,演示应用过程。表4给出了40个样本村及其包含样本养殖场(户)的部分信息。whij表示样本中第h层第i个行政村第j个养殖场(户)的最终抽样权数,即入样概率的倒数。


其中:

=(5 165,13 628,52 738,393 783)

=(5 165,19 336.17,49 493.87,808 619.9)

(1,x1,1ij,x2,1ij,x3,1ij)]=

5 165.0019 336.17 49 493.87808 619.8619 336.175 402 190.230.005 325.3549 493.870.0012 745 885.2846 116.07808 619.865 325.3546 116.073 016 446 228.34
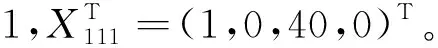


表4 牛羊禽监测调查部分样本信息

表5 第h=1层刀切复制权数和刀切复制值
最后,由式(6)计算出第h=1层牛羊禽存栏量广义回归估计量的方差估计。第h=2层的方差估计步骤相同。表6汇总了全省及各层牛羊禽存栏量的广义回归估计及方差估计。

表6 估计结果
五、结论
本文针对当前中国农业抽样调查估计方法的不足,重点研究广义回归估计量应用于中国农业抽样调查的可行性和适用性,主要结论如下:
第一,随着大数据时代的到来,可应用于中国农业抽样调查的辅助信息有很多,如农业普查数据、历史抽样调查数据、农业行政记录、遥感数据,以及由智能农业机械收集的实地观察数据等,这为构造广义回归估计量提供了重要基础。
第二,利用第三次全国农业普查数据,针对中国畜禽抽样调查,对广义回归估计量在不同抽样设计情形下的统计性质进行仿真模拟。研究结果显示,相比于目前所采用的HT估计量,广义回归估计量的统计性质更优。
第三,实例演示表明,广义回归估计量构造过程易于理解,且当所有调查变量利用的辅助信息相同时,采用刀切法可以同时估计所有调查变量总体参数估计量的方差,实际操作便捷,计算效率高。广义回归估计量在中国农业抽样调查中具有较好的应用价值。
