基于高斯过程算法的日尺度IMERG降水数据与站点数据的融合研究——以湖北省为例

谭伟伟，曾 超，沈焕锋,3,4，田礼乔*

(1.武汉大学测绘遥感信息国家重点实验室，武汉 430079；2.武汉大学资源与环境科学学院，武汉 430079；3.地球空间信息技术协同创新中心，武汉 430079；4.地理信息系统教育部重点实验室，武汉 430079)

作为全球水循环的主要驱动力，降水是气象学、生态学和水文学的一个重要参量，在物质交换和能量平衡中也有重要的作用[1-2].降水数据的精度和空间分辨率往往较低,作为水文模型的重要输入参量，其不确定性会导致水文模型的输出结果具有很大的不确定性，因此提高降水数据的精度和空间分辨率在水文、气象、生态等诸多领域具有非常重要的意义[3].

降水数据可以从地面站点网、雷达降水估计、卫星降水估计等重要的来源中获取.地面观测站的降水观测值仅仅能代表一定范围内的降水特征，具有稀疏和空间分布不均匀的缺点.基于地面站点的降水数据插值以获取更高空间分辨率的面状降水数据，其误差往往比较大，插值数据在地面站点外的区域的误差更为显著[4].天气雷达能提供高时空分辨率的降水数据，但是雷达降水估计的精度受复杂山区的影响很大.过去几十年，多个卫星降水计划得到实施，如GPCP[5]、PERSIANN[6]、TRMM[7]、GSMaP[8]、GPM[9]等.一系列降水卫星的研发和相继升空，使得全球区域的各个区域可以获得降水数据源.遥感卫星为获取时空连续的栅格化降水数据提供了一种重要的来源[10].尽管卫星降水数据丰富了降水数据源，但是卫星降水数据依然有局限性，主要有:受诸多环境因素影响，卫星降水数据的精度往往较低，特别是卫星降水数据的时间分辨率越高，与气象站点观测数据的一致性往往越低；卫星降水数据虽然有覆盖范围广泛的优势，但是其空间分辨率较低，无法满足小流域尺度的研究需求.因此，不同来源的降水数据资料都有其优缺点，如何综合多源降水数据的优点以获取高精度和高分辨率的栅格化降水数据具有重要的意义.

近十多年来，国内外有大量关于降水数据融合的研究，降水数据融合方法为获取高精度和高空间分辨率的栅格化降水数据提供了可靠的思路.国内外提出了多个降水数据融合方法，主要包括最优插值[11]、卡尔曼滤波[12]、贝叶斯估计[13]、概率密度匹配[14]、小波变换分析[15]、变分方法[16]等.目前关于最新一代IMERG卫星日分辨率降水数据的降水融合研究较少.针对日尺度分辨率卫星降水数据的精度和空间分辨率较低的问题，本文利用2016年7月19日湖北省IMERG日降水数据和站点观测数据，采用自适应样条多元回归[17]、随机森林[18]、高斯过程回归[19]三种算法，提出点面融合估计和站点偏差校正估计两个融合方案获取融合的降水数据，并对比了两个融合方案和每个算法的融合效果和精度.

1 研究区域与数据

1.1 研究区概况

湖北省位于中国中部地区，介于29°01′53″～33°16′47″N，108°21′42″～116°07′50″E，总面积约18.59万km2.区域处于地势第二级阶梯向第三级阶梯过渡的地带，地貌类型丰富，包括山地、丘陵、岗地和平原，山地和丘陵约占全省面积80%，地势高低悬殊.湖北省的地形对降水影响较大，降水地域分布呈由南向北递减趋势，且有季节变化规律，一般是夏季最多，冬季最少.6月中旬至7月中旬是梅雨期，降水量最大.图1为研究区和气象站点分布图.

图1 湖北省区域及气象站点分布Fig.1 Locations of rain gauge stations in Hubei province

1.2 研究数据

研究采用降水量丰富的2016年7月19日 的IMERG数据、DEM数据、Bright temperature(BT)亮温数据和气象站点实测数据.IMERG日分辨率降水数据下载自NASA(https://pmm.nasa.gov/data-access/downloads/gpm)，数据覆盖范围为90°S～90°N，空间分辨率为0.1°×0.1°(约10 km).DEM数据来源于地理空间数据云(http://www.gscloud.cn/).BT数据来自NASA的MYDTBGA亮温数据，空间分辨率为500 m×500 m.研究的范围有55个气象站点，数据来源于中国气象局国家气象中心气象数据网(http://data.cma.cn/).以上数据都使用像元聚合的方法重采样到1 km×1 km的空间分辨率，该重采样方法的特点是对采样窗口内部的像元等权加权计算重采样值，能抑制高分辨率辅助数据的异常值或像元值的剧烈变化的影响.

2 降水数据融合

2.1 高斯过程回归模型

高斯过程回归(GPR)在机器学习领域应用比较广泛，具有严格的统计学习理论基础.它在贝叶斯线性回归方法的基础上，用核函数替代贝叶斯线性回归的线性核，因此高斯过程回归在对处理高维数、小样本、非线性等复杂的问题具有很好的适应性，具有泛化能力强的特点.

高斯过程(GP)从函数空间角度上描述函数分布，其性质由均值函数m(x)和协方差函数K(x，x′)决定，形式分别为：

m(x)=E[f(x)]，

(1)

K(x，x′)=E[(f(x)-m(x))(f(x′)-m(x′))]，

(2)

其中x、x′属于Rd为任意随机变量.GP定义为f(x)～GP(m(x)，K(x，x′)).

对于高斯过程回归，假设

(3)

其中，x为输入向量，y为受噪声污染的观测值，f为GP预测的函数值，ε为噪声.

观测值y的先验分布为：

(4)

而观测值y和预测值f*的联合先验分布为：

(5)

由以上可以得出预测值f*的后验概率密度分布为:

(6)

其中

(7)

cov(f*)=K(x*，x*)-

(8)

高斯过程中选择的最广泛的协方差函数为平方指数协方差函数：

(9)

文献[3]提出了一种高时间分辨率的卫星降水数据和气象站点数据的融合方法，该方法的思路求出卫星降水数据相对于站点数据的偏差，使用高分辨率的辅助数据模拟偏差场来求出校正的降水融合数据.本文称该融合方法为站点偏差校正估计方法，并提出点面融合估计方法融合IMERG数据和站点数据.本实验选择GPR算法和使用两种融合方案估计研究区域内的日降水量，核函数采用平方指数协方差函数，并与其他两个统计学习方法包括自适应多元样条回归(MARS)和随机森林(RF)的实验结果作对比.

2.2 点面融合估计方法

假设pf是融合的降水数据，ps是卫星降水数据，po是站点观测数据.点面融合方法估计的步骤如下：

1) 双线性内插0.1°×0.1°分辨率的IMERG降水数据，将IMERG数据降尺度到1 km×1 km的分辨率，表示为IMERGBi；反距离加权法内插点状气象站点数据为1 km×1 km分辨率的面状数据，表示为降水空间因子preps.

2) 训练站点处观测值(po)与各个预测因子之间的模型，模型表示为

po=f(Lon，Lat，DEM，preps，IMERGBi)，

(10)

其中，Lon、Lat、DEM、preps、IMERGBi分别代表气象站点处的纬度、经度、高程、插值的IMERGE降水值、降水空间因子值，f是以站点处的观测值与各个因子训练得到的模型.

3)将第2)步训练的模型应用到1 km×1 km分辨率的面状数据，得到融合的降水数据，表示为

pf=f(Lon，Lat，DEM，preps，IMERGBi，BT)，

(11)

其中，Lon、Lat、DEM、preps、IMERGEBi分别代表相应的1 km×1 km分辨率的面状数据，pf为最终融合的降水数据.图2为该方案1的流程图.

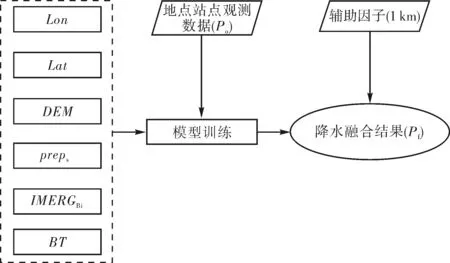
图2 基于点面融合估计的降水融合方法流程图Fig.2 Flow chart of precipitation merging method based on point-to-area estimation

2.3 站点偏差校正估计

偏差校正估计的步骤如下：

1)同2.2的(1)，插值得到IMERGBi和preps.

2)假设融合数据pf，卫星降水数据ps和站点观测数据具有如下关系：

pf=ps+f(po-ps)，

(12)

式中，po-ps即站点观测值与卫星降水数据的差，代表卫星降水的偏差.f(po-ps)表示为：

f(po-ps)=f(Lon，Lat，DEM，

preps，IMERGBi，BT)，

(13)

其中，Lon、Lat、DEM、preps、IMERGBi同2.2的第2)步，f是以站点处的卫星降水偏差值与各个因子训练得到的模型.

3)将第(2)步训练的模型应用到1 km×1 km分辨率的面状数据，估计整个偏差场f′(po-ps)，表示为

f′(po-ps)=f(Lon，Lat，DEM，

preps，IMERGBi，BT)，

(14)

其中，Lon、Lat、DEM、preps、IMERGBi同2.2的第3)步.

4)将插值的IMERGBi(ps)与偏差场f′(po-ps)相加得到偏差校正结果pf，表示为：

pf=ps+f′(po-ps).

(15)

式中，pf为最终融合的偏差校正降水数据.图3为该方案2的流程图.

图3 基于偏差校正的降水融合方法流程图Fig.3 Flow chart of precipitation merging method based Bias correction

3 实验结果和讨论

3.1 日尺度降水融合结果

本文选取2016年7月19日的IMERG降水数据作为例子，保持1 km×1 km高分辨的亮温数据与卫星降水数据的时间同步.分别使用点面融合估计方法(方案1)和站点偏差校正估计方法(方案2)对IMERG日降水数据与站点观测数据融合，并分别使用GPR、MARS、RF三个统计学习方法估计IMERG日降水数据与站点观测数据的融合结果.方案1和方案2的融合结果分别如图4和图5所示.

图4(a)表明原始的IMERG降水图像(图4(a))空间分辨率较低，气象站点数据直接插值的结果(图4(b))相比原始数据虽然分辨率得到提升，但是图像明显很模糊，缺少细节变化信息.利用MARS方法通过方案1融合IMERG数据和站点数据的结果(图4(c))的分辨率得到提升，但是图像细节信息不丰富；RF融合结果(图4(d))有足够的细节纹理信息，但是出现了明显的块状，如图4(d)的最北端的矩形块状和图像中心的圆形块状，这明显不符合降水的分布模式；图4(e)是基于GPR算法点面融合的降水图像，融合结果的图像分辨率和细节信息均有较大的提升，空间变化合理，且改善了反距离加权插值带来的“牛眼效应”.

使用方案2的流程对IMERG降水数据和站点数据融合的结果(图4(c)～(e))均能提升IMERG降水数据的空间分辨率.通过比较两个方案的融合结果，图5(c)相比于图4(c)，其空间细节信息得到改善；图5(d)仍然出现图4(d)的块状现象，采用偏差校正方法不能避免块状问题；图5(e) 明显优于图5(c)～(d)的融合效果，且相比于图4(e)变化不大，但是图5(e)保留了IMERGBi的几处插值痕迹.

3.2 精度验证

气象站点数据用于融合结果的精度验证，精度验证的最常用的方法有保留交叉验证、K折交叉验证和留一交叉验证法.研究区域内的站点数较少，本文选择留一交叉验证法，即假设站点数为N，每次使用N-1个站点建模并预测剩下的站点处的融合值，该过程循环N次以保证所有的站点都参与精度评价过程.精度评价选择的量化指标有相关系数R，均方根误差RMSE和偏差Bias.R表示融合的降水数据与站点观测数据的一致性，相关性越高则R越接近1；RMSE表示评价融合数据的整体误差；Bias表示数据的系统误差，评价融合结果的偏离程度.三个指标的计算公式如下：

(16)

(17)

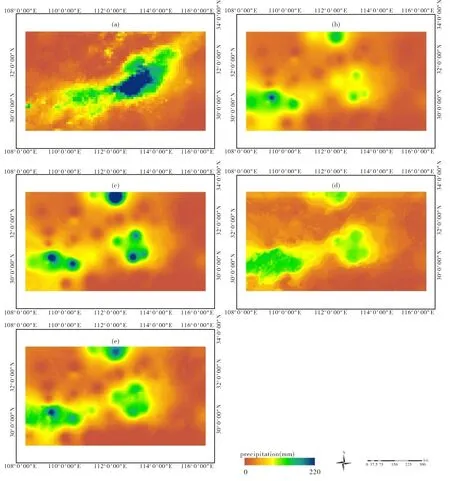
图4 IMERG数据(a),站点插值数据preps(b),基于MARS(c),RF(d),GPR(e)的点面融合方法的融合数据Fig.4 Comparison of (a) IMERGE precipitation，(b) preps，the merged results by point-to-surface fusion method using (c) MARS，(d) RF，and (e) GPR

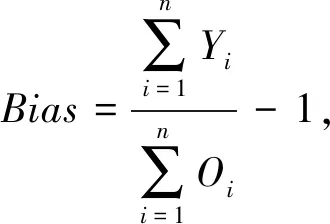
(18)

本文用气象站点数据评估IMERG降水数据的原始精度，作为与融合数据的精度对比的参照，图6为精度评价结果.从图6可得，该日尺度的精度较低(R=0.43，Bias=0.07%)，无法满足气象、水文等领域对高精度卫星降水数据的需求.

本文以站点降水数据为真值，用留一交叉验证法定量评估两种融合方案的效果，站点验证结果如表1所示，其中GPR_1表示使用方案1的GPR融合结果，GPR_2表示使用方案2的GPR融合结果，其余类似.

从模型精度结果来看，两种方案的模型训练的精度(R)都很高，站点处的拟合效果都比较好，因此比较模型的泛化能力更重要.留一交叉验证结果表明，对于两种融合方案，GPR的精度最高，都优于RF的融合结果，而MARS方法表现最差.对比方案1和方案2，方案1的三种算法的融合结果也都优于方案2.因此偏差校正融合方案相比点面融合估计没有任何优势.对比最佳的降水融合结果(GPR_1)和原始的IMERG降水数据，融合结果的精度得到较大的提升，R从0.43提升到0.79，Bias从0.07%降低到-0.02%.

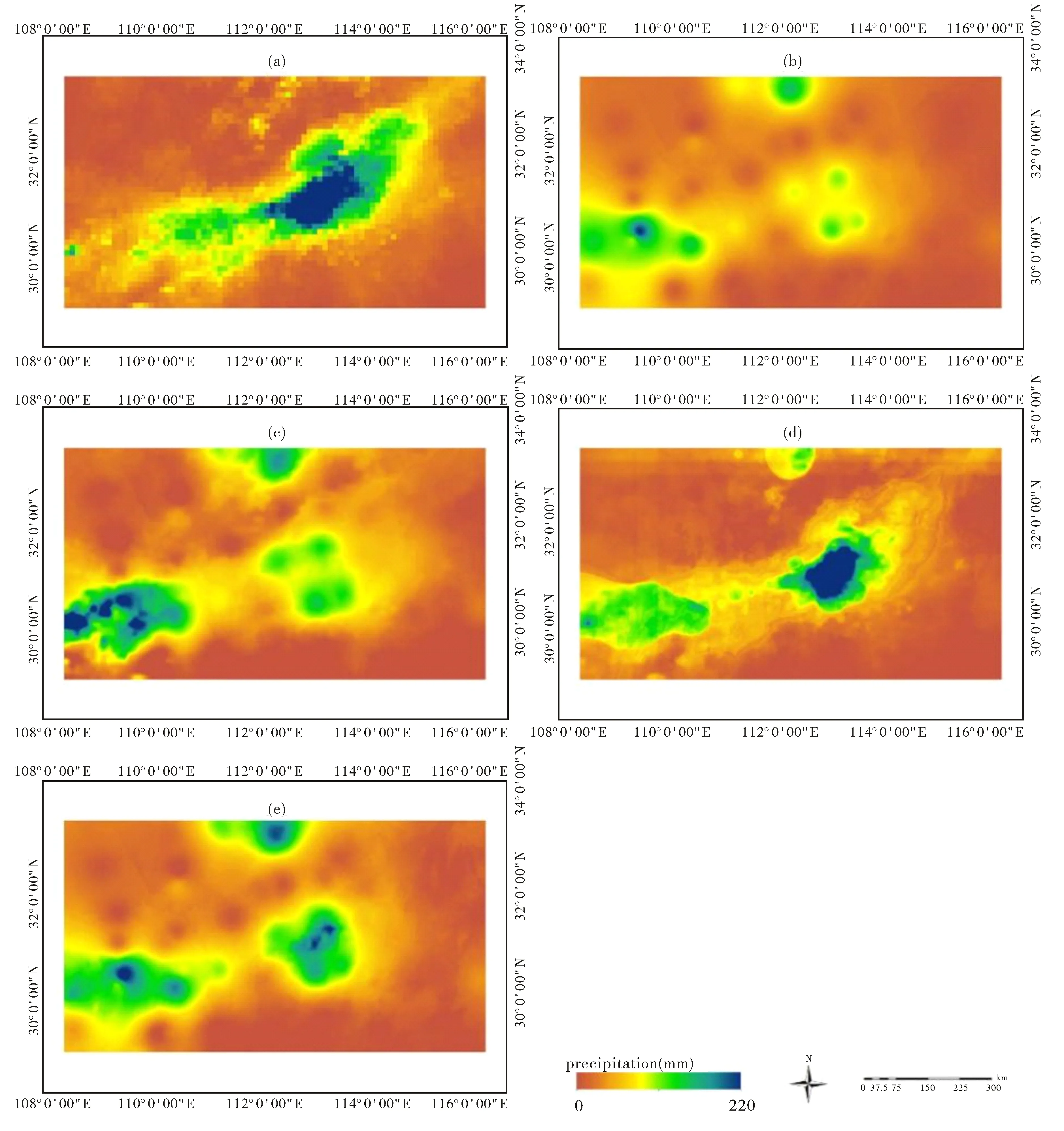
图5 IMERG数据(a),站点插值数据preps(b),基于MARS(c),RF(d),GPR(e)的偏差校正方法的融合数据Fig.5 Comparison of (a) IMERG precipitation，(b) preps，the merged result by bias-correction fusion method using (c)MARS，(d) RF，and (e) GPR

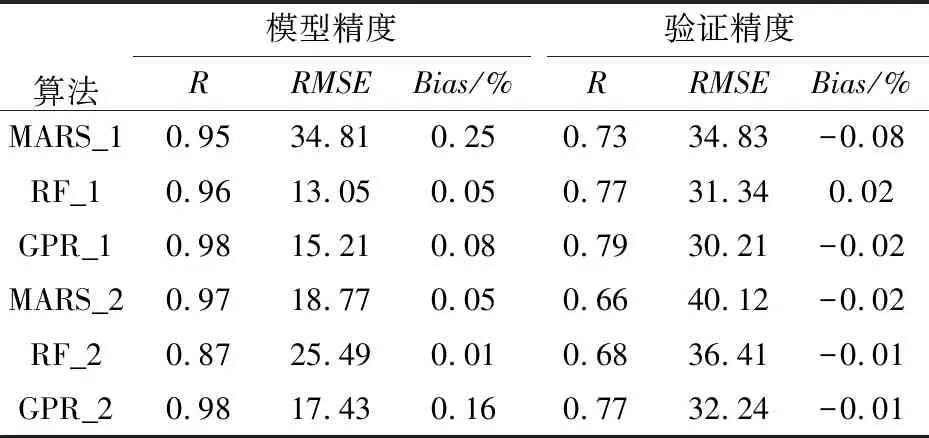
表1 两种融合方案的模型精度和降水融合结果的验证精度Tab.1 Model performances and validation performances of the above two merging schemes

图6 2016年7月19日IMERG降水数据精度评估结果图Fig.6 The accuracy evaluation result of IMERG precipitation data on July 19,2016

4 讨论和结论

4.1 实验结果讨论

方案2估计卫星降水数据和气象站点数据的偏差场，本质上也是点面融合.方案2相比方案1，增加了偏差计算的步骤，估计的偏差场与插值的IMERGBi数据相加，反而使最终的融合结果受到IMERGBi插值痕迹的影响比较大，最终影响融合结果的精度.

随机森林方法本质上是一种回归树，传统的回归树算法采用节点分裂机制，即对训练数据集进行划分，该机制会导致融合结果在空间上有被划分的块状痕迹.自适应多元样条回归采用前向选择和后向删除的机制，对训练数据集尤其是对于小样本数据集非常敏感，在样本稀疏的情况下容易造成非常平滑且有极端值的结果，因此该方法不适用于融合稀疏分布的站点数据与卫星降水数据.

4.2 结论

本文选择日分辨率的IMERG卫星降水数据和站点观测数据两种降水数据资料，并考虑经纬度、DEM、亮温数据、插值的IMERG数据等作为高分辨率的辅助变量，利用高斯过程回归算法结合点面融合估计和站点偏差校正估计两种方案融合两种降水数据资料，并与随机森林、自适应样条多元回归的结果作对比.首先对IMERG卫星降水数据做精度评估，评估结果表明IMERG数据与站点观测数据的不一致较高(R=0.43，Bias=0.07%)，然后从融合图像的结果定性分析每个方案的融合效果，最后使用站点观测数据作为真值定量评价融合数据的精度.实验结果表明：

1) RF融合结果会出现块状痕迹，MARS方法的融合结果很模糊，而提倡的GPR方法的融合结果变化合理，且细节信息优于站点数据直接插值的结果.

2) 三种算法的点面融合的精度都优于基于偏差校正融合结果的精度，且避免了偏差校正的融合结果保留的IMERG数据的一些插值痕迹.

3) 使用GPR方法对IMERG卫星降水数据和站点观测数据做点面融合，融合结果的精度(R=0.79，Bias=-0.02%)相比原始的卫星降水数据有较大的提升，该方案可对日分辨率降水数据的融合提供一个有价值的参考.

尽管本文提出的基于GPR的点面融合方法能改善IMERG数据的质量，但是该方法的融合结果仍然不能完全消除IMERG插值数据的痕迹，还需要更深入地研究如何完全消除插值数据的影响.