车轮多边形对车辆动力学性能影响分析
2020-06-18王红兵李国芳王泽根丁旺才
王红兵,李国芳,王泽根,丁旺才
(兰州交通大学机电工程学院,兰州 730070)
随着高速列车运行速度的不断提升,载运量及轴重不断加大,车轮与钢轨之间的相互作用力不断增强,列车车轮的磨耗问题也愈发突出。列车在行驶一段里程后,车轮踏面就会出现不同程度的多边形磨损。车轮多边形的出现会引起车辆/轨道系统一系列动力响应的变化,使车辆动力学性能恶化,产生强烈的轮轨噪声,降低乘客乘坐的舒适度以及列车运行品质,对铁路车辆系统的关键结构造成损伤甚至破坏,严重情况下会威胁到行车安全[1-2]。
近些年针对车轮多边形磨耗及其引起的动力学问题,国内外学者进行了大量研究。Morys[3]等建立了ICE-1型高速列车动力学模型和柔性轨道模型,结合迭代长期磨损模型,研究了车轮多边形的起因和发展规律;Johansson和Nielsen[4]认为使用三爪卡盘进行型面切削时车轮形成初始的三阶多边形,并分析了不同谐波阶数下车轮多边形对轮轨垂向力与轨道振动的影响,提出可依据扁疤的幅值开展车轮镟修。王忆佳[5]采用车轮圆周轮廓法来建立了更为准确的车轮多边形模型,分析了高速车轮多边形对车辆动力性能的影响,给出不同列车运行速度下各阶车轮多变形的幅值限值。刘韦等[6]建立刚柔耦合动力学模型,将轮对视为弹性体研究了直线电机地铁车辆轮对弹性对车轮振动、车轮多边形化及轮轨相互作用的影响。周新建、肖乾等[7-8]基于UM建立了车辆/轨道耦合动力学模型,以常见的车轮谐波磨耗为对象研究了车轮谐波磨耗对高速轮轨接触特性的影响。尹振坤[9]以某城际动车组列车原型,建立高速车辆/轨道耦合动力学模型和车轮多边形不平顺输入模型,分析了列车运行速度、车轮多边形幅值及其阶数等因素对轮轨垂向力的影响规律。胡晓依、宋志坤等[10-11]建立了基于柔性轮轨的车辆/轨道系统动力学模型,研究了车轮谐波磨耗对高速轮轨系统振动的影响。
为了更加深入地研究车轮多边形磨耗对高速车辆系统动力学的影响,以CRH2型动车组为研究对象,应用多体动力学软件UM和有限元软件ANSYS建立考虑轮对柔性的车辆/轨道耦合动力学模型,分析车轮多边形阶数和幅值的变化对轮对振动特性、非线性临界速度和轮轨力等车辆动力学性能的影响。
1 轮轨滚动接触简化理论
轮轨滚动接触简化理论是Kalker借助线性接触理论发展的快速计算模型,其快速计算方法FASTSIM是车辆系统动力学数值计算最常用的蠕滑理论之一[7]。该理论建立在以下基本假设的基础上:
(1)接触区中的任一点弹性位移仅和作用在该点的力有关;
(2)接触点某方向的位移仅与同方向的力有关;
(3)接触点的力和位移呈线性关系。
由简化理论计算得到接触面上的切向力分量为

(1)
由简化理论分析得到接触面上的切向力分布为

(2)
式中,a,b分别为椭圆接触斑的长短轴;ξ,η,φ分别为纵向蠕滑率,横向蠕滑率和自旋蠕滑率;Fx,Fy分别为纵向蠕滑力和横向蠕滑力;px,py,pz分别为接触区域内纵向,横向和垂向压应力;N为轮轨法向力;Li为接触点的柔度系数。
2 建立刚柔耦合车辆模型
基于多体动力学理论,结合CRH2型客车动力学参数对转向架的悬挂装置进行力元简化,在UM中建立考虑轮对柔性的刚柔耦合车辆动力学模型[12-13],如图1所示。添加车轮踏面,轨道不平顺等仿真参数,设置车轮多边形阶数为20,幅值为0.05 mm,进行多刚体模型和刚柔耦合模型的对比分析,验证应用刚柔耦合模型的必要性。表1为柔性轮对前42阶模态分析的结果,图2、图3为两种模型的时域和PSD对比图。

图1 刚柔耦合车辆模型
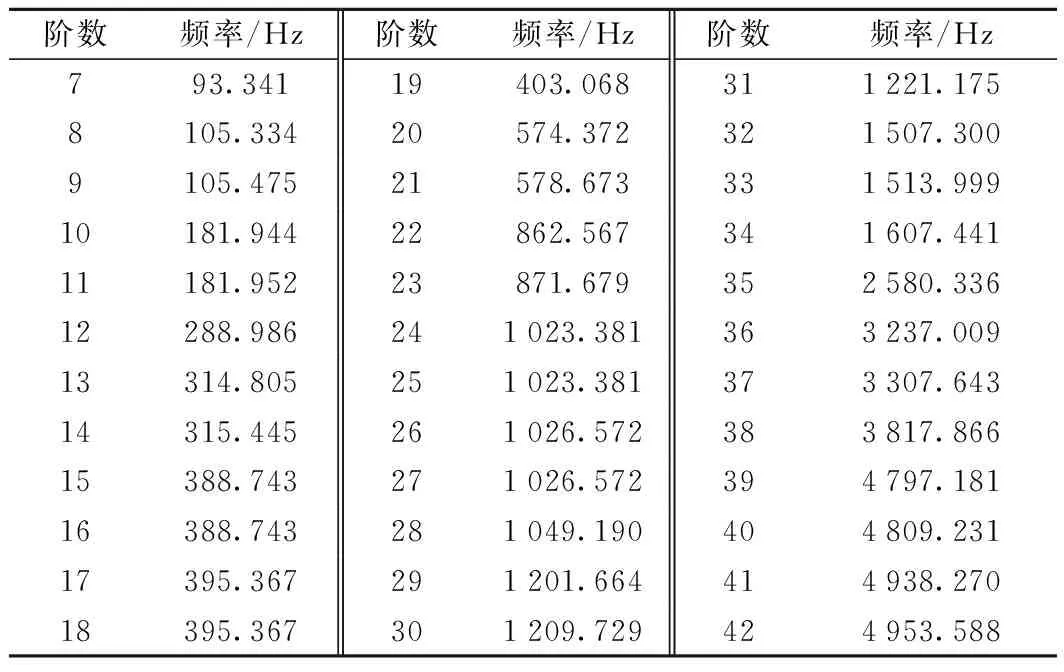
表1 柔性轮对模态分析结果
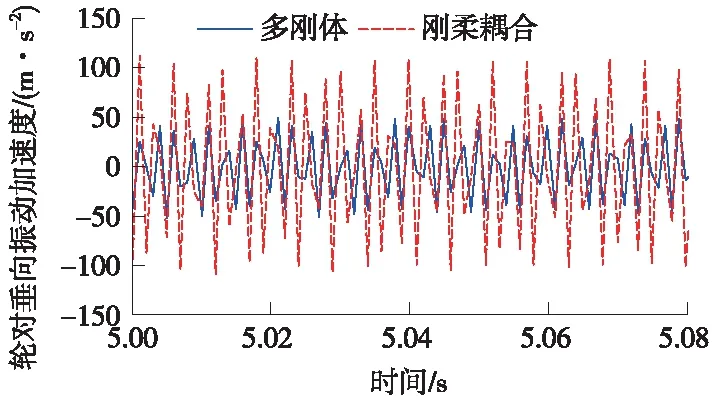
图2 轮对垂向振动加速度时域

图3 轮对垂向振动加速度频域
由图2、图3可知,刚柔耦合模型中轮对垂向振动更为剧烈,最大加速度为134.82 km/s2,而多刚体模型对应的垂向振动加速度最大仅为59.89 km/s2,频域图中两模型均出现411 Hz的主频,但刚柔耦合模型在该频率的幅值较大。可见考虑轮对为柔性体后,轮对的垂向振动响应比多刚体模型大很多,且20阶的车轮多边形的特征频率411 Hz接近柔性轮对的第19阶垂向振型模态的固有频率403 Hz,说明20阶车轮多边形引发了柔性轮对的垂向共振模态,加剧系统中垂向振动的动态响应,也延长了激扰过后系统恢复稳定耗费的时间。刚柔耦合模型与实际车辆的运行响应状况更加贴近,因此考虑轮对为柔性的刚柔耦合模型更加真实也非常有必要。
3 车轮多边形对轮对振动特性的影响
根据车轮多边形的阶数及列车运行速度可计算出车轮多边形的特征频率[14],计算公式如下。

(3)
式中,N为车轮多边形阶数;v为列车运行速度;r为车轮名义滚动圆的半径。
160~240 km/h这5个速度工况下,2~20阶所对应的车轮多边形的特征频率如表2所示。
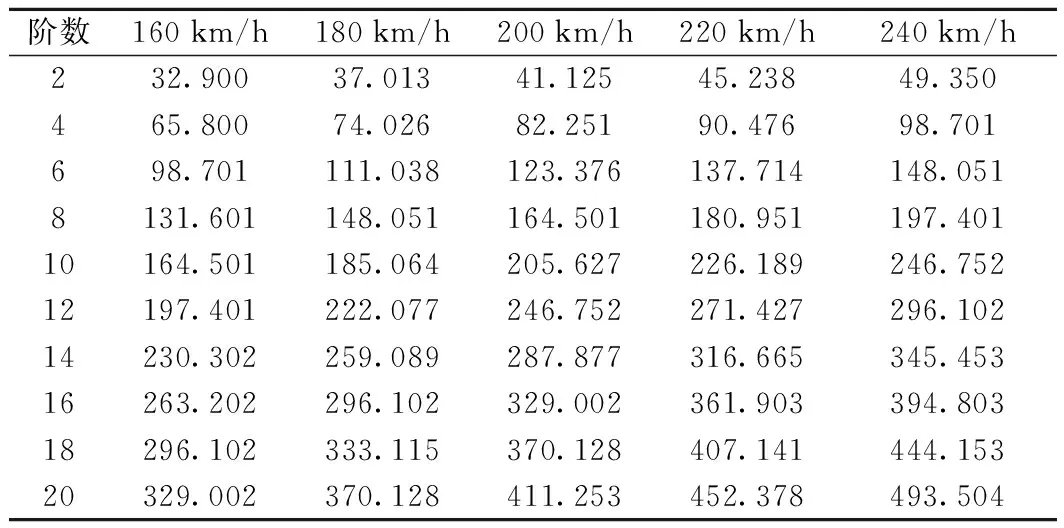
表2 车轮多边形的特征频率 Hz
随着车轮多边形阶数以及速度工况的变化,当多边形的特征频率与轮对某阶振型模态的自身频率相近或重合时,将引发轮对的共振现象,加剧轮轨间的动态作用。
研究车轮多边形对轮对振动特性影响时,测取1位轮对垂向振动加速度与轮对垂向位移,选取最大值进行对比分析。速度工况设置为160,180,200,220,240 km/h共五种工况,每种工况下均有一组正常车轮的对比数据。研究多边形阶数对轮对振动特性的影响时,幅值设定为0.05 mm,阶数设置有2,4,6,8,10,12,14,16,18,20阶;研究多边形幅值对轮对振动特性的影响时,阶数设定为20阶,幅值设置有0.01,0.02,0.03,0.04,0.05 mm。仿真结果如图4、图5所示。

图4 不同阶数时轮对垂向振动加速度
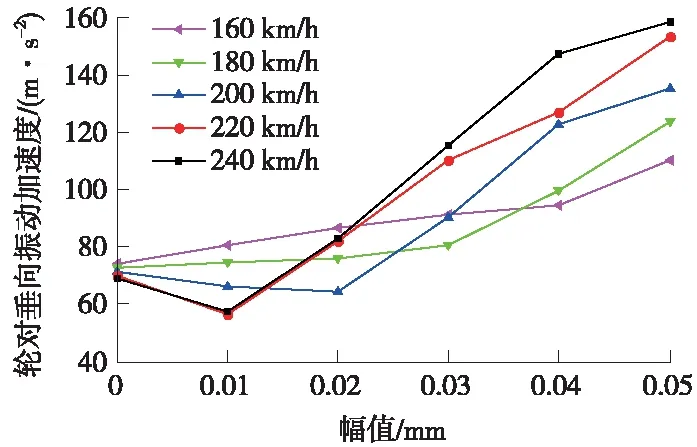
图5 不同幅值时轮对垂向振动加速度
由图4、图5可知,轮对垂向振动加速度随速度增加而呈上升趋势,随着阶数增加轮对垂向振动加速度普遍也呈上升趋势。在240 km/h速度工况中,阶数为8时轮对垂向振动加速度出现一个极值,该阶车轮多边形的特征频率为197 Hz,与此相近的轮对振型频率是181 Hz,由于频率差距使振动情况并不剧烈,但相较于前后两阶的振动情况要大一些。该工况下16阶时轮对垂向振动加速度达到最大值160.51 m/s2,该阶多边形的特征频率394 Hz与19阶轮对垂向振型模态的固有频率403 Hz最为接近,使得共振现象更明显。在220 km/h速度工况下,18阶多边形时轮对的垂向振动加速度达到最大163.54 m/s2,该阶多边形的特征频率为407 Hz,与403 Hz相离最近,垂向共振达到最大。
轮对垂向振动加速度随车轮多边形幅值增长呈线性上升趋势,并且速度越大,轮对垂向振动加速度增长的斜率越大,上升范围就越广。160 km/h速度工况下,该参量的变化幅度为38.10 m/s2,而240 km/h速度工况下该参量的变化幅度为91.98 m/s2,为低速160 km/h的2.4倍。
4 车轮多边形对动力学性能影响分析
4.1 运动稳定性能分析
(1)非线性临界速度
首先采用降速法测正常车轮情况下该模型的临界速度,初始速度为530 km/h,将速度作为横轴,轮对横向位移作为纵轴,观察轮对横向位移随速度下降的变化情况,仿真结果如图6所示。
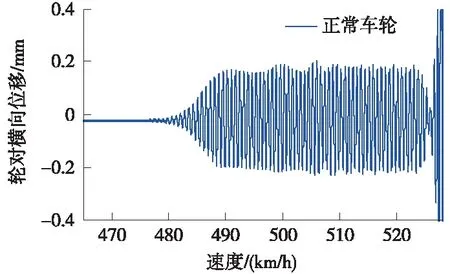
图6 非线性临界速度
为了准确得到标准车轮情况下的临界速度值,需对485~493 km/h速度范围的轮对横向位移进行逐一计算。结果如图7、图8所示。

图7 v=489 km/h

图8 v=490 km/h
由图7、图8可知,当速度为489 km/h时,随着时间的推移,轮对的横向位移会逐渐收敛到稳定范围,而速度为490 km/h时,无论仿真时间多长,轮对的横向位移终究不会收敛,一直处于发散不稳定状态。最终确定临界速度为489 km/h。
车轮多边形阶数和幅值对临界速度的影响如图9、图10所示。
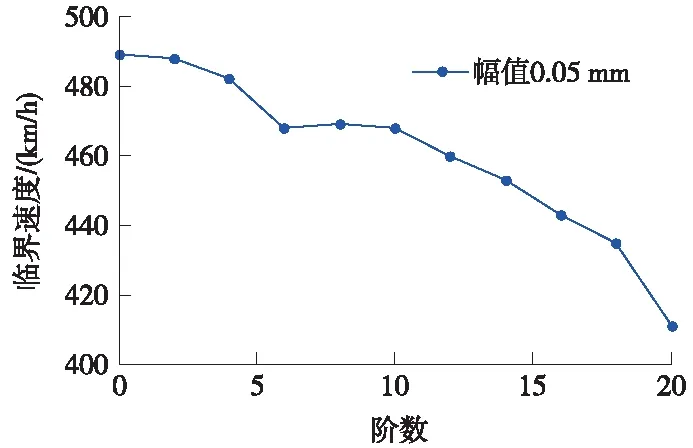
图9 不同阶数时临界速度

图10 不同幅值时临界速度
临界速度随多边形阶数的增加总体上呈下降趋势,与正常车轮情况下的临界速度相比差距越来越大。6~10阶多边形时临界速度变化幅度大大减小,维持在468 km/h左右,之后随阶数增加临界速度又继续下降,到20阶时临界速度降为411 km/h,降低的幅度为正常车轮值的16%。
临界速度随多边形幅值变化时,幅值增加则临界速度减小,并且减小幅度均匀,无剧烈变化。
由此可以得出,车轮多边形对临界速度的影响较大,尤其是高阶、高幅值的车轮多边形时的临界速度,与正常车轮情况的差距甚远。
4.2 运行安全性能分析
(1)脱轨系数
脱轨系数是根据车轮爬轨脱轨条件制定的,考虑轮轨之间爬轨脱轨临界条件并考虑一定的安全裕量制定评价限值,该指标值是轮轨横向力和轮轨垂向力的比值。车轮多边形阶数和幅值对脱轨系数的影响如图11、图12所示。
由图11、图12可知,脱轨系数受低阶多边形的影响较大,并且速度越低越明显,然后随着阶数的再次上升,脱轨系数逐渐达到稳定水平,高阶多边形对脱轨系数的影响较小。在160 km/h速度工况中,脱轨系数先随低阶(2~10阶)多边形的增长而缓慢上升,到10阶时脱轨系数达到稳定水平0.22,此后随阶数上升脱轨系数变化不明显;在180 km/h速度工况下,8阶多边形的脱轨系数就已上升至稳定水平;200 km/h速度工况下6阶时达到稳定水平;220 km/h速度工况下在4阶时就达到稳定水平;240 km/h速度工况下脱轨系数一直受阶数变化影响很小,直至20阶多边形时,脱轨系数快速上升至0.26,但较于脱轨系数的安全限值1.0,0.26则远远小于1.0,表明阶数变化对脱轨系数的影响很小,完全符合车辆运行的安全标准。
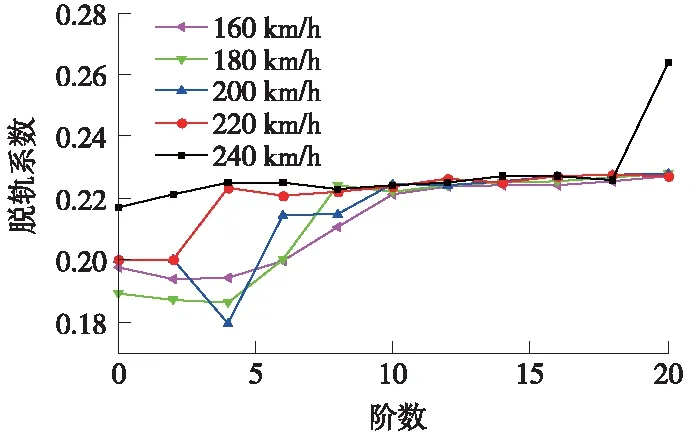
图11 不同阶数时脱轨系数

图12 不同幅值时脱轨系数
脱轨系数随车轮多边形幅值变化时,该参量表现出随幅值增加而缓慢上升的状态,逐渐趋于稳定。各个速度工况下脱轨系数的最大值分别为0.22,0.23,0.23,0.23,0.26。满足脱轨系数的安全裕度限值。
(2)轮重减载率
轮重减载率是评定因轮重减载过大而引起脱轨的另一种脱轨安全指标,为轮重减载量与该轴平均静轮重的比值。车轮多边形阶数和幅值对轮重减载率的影响如图13、图14所示。
由图13、图14可知,轮重减载率随列车运行速度的提高而增加。轮重减载率随车轮多边形阶数变化时,2、4阶对其影响很小,几乎与正常车轮情况下的轮重减载率相等。之后随阶数增加轮重减载率发生较大幅度变化,原因是多边形的特征频率与柔性轮对某阶振型的固有频率接近,两者相差越小则共振现象越明显。160,180,200 km/h速度工况下轮重减载率随阶数变化的最大值分别为0.50,0.57,0.58,均小于轮重减载率的安全限值0.60,能够保证列车运行安全;在220 km/h速度工况下,只有10阶多边形时轮重减载率达到0.63,虽达到合格标准但已超出安全裕度限值;在240 km/h速度工况下,8阶多边形时轮重减载率就已达到0.64,之后随着车轮多边形阶数的增长最大值可达0.74,严重超出了该参量的安全限值。

图13 不同阶数时轮重减载率
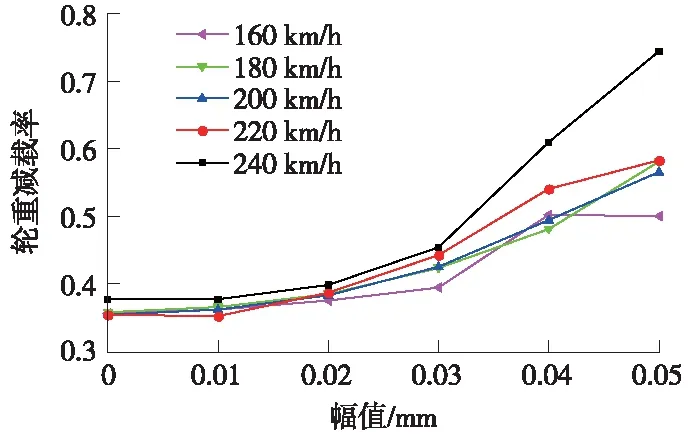
图14 不同幅值时轮重减载率
轮重减载率随多边形幅值的增加呈上升趋势,幅值越大,轮重减载率值越大。5个速度工况下轮重减载率随幅值增加的最大值分别为0.50,0.57,0.56,0.58,0.74,且240 km/h速度工况下幅值为0.04 mm时轮重减载率值为0.61,超出了我国标准限值。因此车轮多边形对轮重减载率的影响较大。
(3)轮轨垂向力
轮轨间的垂向冲击对车辆和轨道均有不利影响,是限制车辆轴重和提速的重要因素。车轮多边形阶数和幅值对轮轨垂向力的影响如图15、图16所示。

图15 不同阶数时轮轨垂向力

图16 不同幅值时轮轨垂向力
由图15可知,轮轨垂向力随速度的上升而增加。该参量随多边形阶数变化时总体呈上升趋势。160~240 km/h速度工况下轮轨垂向力随阶数变化的最大时分别为108,111,122,136,141 kN,均小于我国的轮轨垂向力限值170 kN。
由图16可知,轮轨垂向力随幅值的上升普遍呈线性增长的趋势,速度高的工况出现一些小的波动,但轮轨垂向力的最大值也都满足限值标准。与正常车轮情况下的轮轨垂向力相比,车轮多边形对轮轨垂向力的影响较大,但轮轨垂向力的最大值均小于限值,所以满足车辆运行安全的要求。
4.3 运行平稳性能分析
高速客车的运行平稳性主要是针对客车上旅客的乘坐舒适度评价车体振动的指标,主要根据车体加速度通过数理统计的方法得到。车轮多边形阶数和幅值对Sperling指数的影响如图17~图20所示。

图17 不同阶数时横向Sperling指标

图18 不同幅值时横向Sperling指标

图19 不同阶数时垂向Sperling指标
横向Sperling指标随运行速度的提高而增加,车轮多边形的阶数和幅值对横向Sperling指标的影响都很小,与正常车轮情况时的横向Sperling指标非常接近,这种影响可以忽略不计。160~240 km/h这5个速度工况下受车轮多边形影响的最大值分别为1.73,1.79,2.03,2.09,2.18,均小于客车1级平稳性能限值2.5,达优级水平。

图20 不同幅值时垂向Sperling指标
垂向Sperling指标的变化规律与横向Sperling指标相似,并且车轮多边形对垂向Sperling指标的影响更为微小,几乎与正常车轮情况的相等。160~240 km/h这5个速度工况下受车轮多边形变化的垂向Sperling指标分别保持在1.43,1.50,1.71,1.78,1.80,也都符合我国客车1级平稳性能标准,达到优级水平。
综上所述,车轮多边形对平稳性能的影响甚微,主要是因为一系和二系减振器的减振作用。
5 制定车轮多边形幅值限值
由于车轮多边形对轮重减载率的影响很大,为了保证列车有良好的运行安全性能,有必要制定车轮多边形幅值的限值,将轮重减载率控制在限度0.6之内,并且也可以为车轮踏面的镟修提供参考,车轮多边形发展到一定程度需要经过镟修来改善踏面外形,制定幅值限值后可据此来对车轮进行精确的镟修加工,避免加工次数太多带来的昂贵成本和构件寿命的折损,也能确保列车运行的安全性。
车轮多边形对轮轨垂向力的影响也较大,为了确保列车不会因轮轨垂向力太大而发生脱轨事故,要使这些幅值限值工况的轮轨垂向力也满足我国标准,即均小于限度170 kN,对限值工况进行仿真。根据轮重减载率制定的幅值限值工况的轮轨垂向力均未超限,其最大值仅为139.39 kN,都满足我国轮轨垂向力限度标准。因此综合这两个因素制定出的车轮多边形幅值随速度、多边形阶数变化的限值如图21所示。
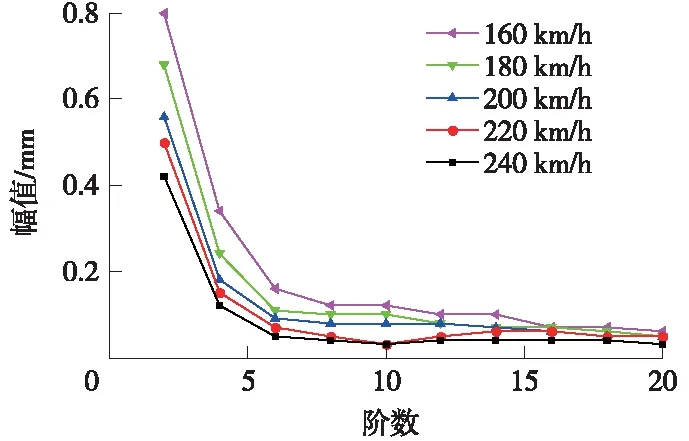
图21 车轮多边形幅值限值
由图21可知,多边形幅值限值随运行速度的升高而降低,并且多边形阶数越小,幅值的限值越大,尤其是2~4阶其幅值限值更高。
6 结论
本文研究了不同速度工况下2~20阶、幅值0.01~0.05 mm的车轮多边形对车辆动力学性能的影响并进行分析,得出如下结论。
(1)研究车轮多边形问题时,考虑轮对柔性的车辆动力学模型更能反映真实运行情况。
(2)非线性临界速度随多边形发展而呈下降趋势,因此对运动稳定性的影响较大;车轮多边形对运行平稳性的影响很小,可忽略不计。
(3)车轮多边形对脱轨系数的影响较小;车轮多边形对轮重减载率的影响很大,轮重减载率随车轮多边形发展呈上升趋势,240 km/h速度工况下8阶时轮重减载率达到0.64,超出我国标准限值;轮轨垂向力随多边形的发展总体呈上升趋势,但该参量值均小于我国的轮轨垂向力限值170 kN,不会发生脱轨事故。
(4)为保证行车安全,综合轮轨垂向力和轮重减载率限值制定车轮多边形不同速度工况、不同阶数的幅值限值,为车轮旋修提供参考依据。
