一种计盒维数估算的新方法

王晓燕，陈志杰，姜友华，唐文澜，薄乾祯

(1.湖北大学资源环境学院，湖北省农业遥感应用工程技术研究中心，湖北 武汉 430062;2.武汉大学土木建筑工程学院，湖北 武汉 430072)

0 引言

所谓分形(Fractal)，原意为破碎和不规则，用以指那些与整体以某种方式相似的部分构成的一类形体，如海岸线的弯曲、植物的分支、浮云的轮廓、山脊的形态、晶体的生长和流体的渗透等，其基本特征是自相似性(Self-similarity).分形理论最早由美籍法国科学家B. Mandelbrot创立，该理论用分形维数(Fractal dimension)(简称分维)的概念来度量自然现象的不规则程度，不仅可以揭示事物内部的自仿射或自相似特性，还可以揭示复杂系统的工作原理.经过近30年的发展，已经被广泛地应用于各种社会科学和自然科学领域[1].分形维数是刻画目标分形特征的一个重要参数，其定义有很多，而且对同一物体以不同方式定义或侧重面不同，其分形维数也各不相同[2].常用的分维有Hausdorff维数、计盒维数、相似维数、信息维数和关联维数等，其中计盒维数又是一种使用最为广泛的维数之一.如计盒维数可用于分析生态学中植物群落分布格局特征及其尺度变化特征[3]，也可以反映自然界中水系的空间分布特征和内部结构[4]；在云雾遥感监测中，采用计盒维数法与其他方法结合起来进行云雾的识别和分离[5]；此外，计盒维数在图像特征、声波信号分形特征提取等方面也有广泛的应用[1,6].然而，在计盒维数的实际估算中，还有一些问题是广大学者十分关心和感到困惑的.正如陈彦光指出，许多基本问题尚未解决，这些问题包括：测量尺度问题、标度区的识别问题和统计分析标准的确定问题等[7].总体来说，目前的情况仍然是，在计盒维数估算中，尚缺乏一种可操作的实用方法.

由于数学上标准分形体都有确切的理论分维值[8-9]，本文中采用3种标准的两维分形体(Koch曲线、Sierpinski三角形垫片、Vicsek分形)为实验对象，揭示盒子大小、盒子数量、盒子递减方式、盒子递减速率和标度区判断等对计盒维数估算的影响，并在此基础上提出相应的建议和解决问题的具体方法，这为计盒维数的准确和快速估算提供理论依据.

1 计盒维数估算中涉及的若干问题

计盒维数(box dimension)概念比较清晰，计算相对简单，并且对于是否具有自相似特性的图像均适用，是分形分析中较为直观实用且使用最广泛的一种.实际应用中可形象地理解为，在集合F中(可以是线、面或体)，构造一些边长为r的正方形(体)(或称为盒子)去覆盖集合，计算不同r值的“盒子”和F相交的个数N(r)，由N(r)与r在双对数坐标系中直线的斜率值可求得计盒维数D.D是传统意义上尺度为r的计盒维数，用以表征相同形状的小集合覆盖一个集合的效率.

logN(r)=-Dlog(r)+C

(1)

在计盒维数的实际估算中，盒子大小、盒子数量、盒子递减方式、盒子递减速率以及标度区识别等是我们经常碰到的棘手问题.

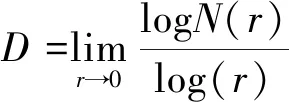
计盒维数的估算中，当盒子尺度太大时，盒子不能很好刻画分形体，从而使分维估算效果不佳；当盒子尺度小到一定程度，盒子可以更好地逼近分形体.但是，当尺度进一步小到一定程度之后，就会达到分辨率的极限.实际上，严格意义上的分形体仅存于数学世界，即使在数字化环境下采用计算机生成的分形图形，得到的图形分辨率也是有限的.因此，当尺度小到一定程度之后，就会达到分辨率的极限.所以，盒子尺寸不应该是无限小、而应该是不大不小.

1.2 盒子数量实际分维估算中，我们总是希望盒子数量越多越好，这是因为如果盒子数量太少，级别不够，也不利于逼近不同细节的分形体.一般来说，盒子数量多一是比较的.但是，根据我们的大量实验，如果使用很小的盒子衰减速率(如ε=0.80)，盒子数量必然很多，对于线状地物估算的分维值越接近1.0，对于面状地物估算的分维值越接近2.0，这与真实值有很大差异，这常令人困惑的问题之一.所以，盒子数量并不是越多越好，只需要保持适当的数量即可.

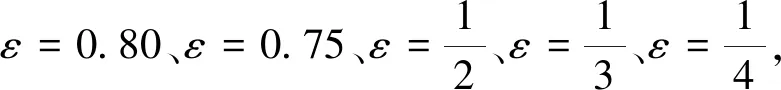
如果采用算术递减方式，在实际计算中，很难把握盒子大小和盒子数量.相对而言，指数递减方式可以使盒子比较快速地变小，盒子数目与盒子大小的乘积能比较快速逼近测量对象的某个测度(长度、面积或者体积)，容易捕捉分形体可能存在的等级体系递阶结构特征.实际上，在分维估算过程中，既可以采用指数递减测度，也可以采用算术递减测度.但是，在绝大多少情况下，算术递减尺度并不优于指数递减尺度[7].也即，测度的盒子最好采用指数方式递减.

表1 盒子大小与盒子数量关系(Koch曲线)

3)对于自然图形，建议采用递减速率：ε=0.75或ε=0.80.因为无法判断自然图形分形体结构，我们不清楚采用何种递减速率可以更好地逼近分形体，所以建议采用递减速率：ε=0.75或ε=0.80，这种递减速率可以使盒子的慢慢递减，更容易逼近自然图形的不同细节，分维估算效果更好.

1.5 标度区判断方法标度区识别是一个十分关键的问题.分形是一种分布广泛的具有标度性质的现象.测量尺度与相应测度的幂律关系通常仅在一定尺度范围内有效，从而形成所谓标度区.也就是说，双对数坐标上不是一条直线，而是两条以上的直线段[7].但是，如何判断标度区，我们尚缺乏可操作的实用方法，这里我们提出一种标度区判断的新方法.

根据不同尺度下覆盖目标的总长度(或总面积)曲线，通过目视判别方式就可以看出：当盒子太大，总长度(或总面积)波动很明显时，就需要剔除前面这些对数点对；当盒子变小，总长度(或总面积)基本上不随盒子变小而发生变化时，就需要不选取后面这些对数点对.也就是说，仅仅保留中间的对数点对.具体来说：

①若目标图形为线型，则沿横轴方向，将每相邻两点构成的直线，直线的斜率大于零且后续不存在斜率小于零的第一个点作为最大盒子，或者直线的斜率小于零且后续不存在斜率大于零的第一个点作为最大盒子，直线的斜率近似于零的最后一个点作为最小盒子，从而得到分维估算的合理尺寸的盒子组.

②若目标图形为面型，则沿横轴方向，将每相邻两点构成的直线，直线的斜率小于零且后续不存在斜率大于零的第一个点作为最大盒子，或者直线的斜率大于零且后续不存在斜率小于零的第一个点作为最大盒子，直线的斜率近似于零的最后一个点作为最小盒子，从而得到分维估算的合理尺寸的盒子组.

2 计盒维数估算新方法验证

由于3种严格分形体(Koch曲线、Sierpinski三角形垫片、Vicsek分形)有确切的分维理论值，下面就以这3种标准分形体为研究对象，验证本文中提出的建议和相关方法的实验效果.

2.1 Koch曲线、Sierpinski三角形垫片、Vicsek分形Koch曲线是1904年瑞典数学家Koch构造的几何图形.Koch曲线的生成过程：第一步，给定一个初始图形为一条线段；第二步，将这条线段中间的1/3处向外折起；第三步，按照第二步的方法不断的把各段线段中间的1/3处向外折起.如此循环下去最终即可构造出Koch曲线(图1).

图1 Koch 曲线

Sierpinski三角形是由波兰数学家Sierpinski在1915年提出.先作一个正三角形，挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形)，然后在剩下的小三角形中又挖去一个“中心三角形”，如此循环下去就得到高级Sierpinski三角形垫片(图2).

图2 Sierpinski三角形垫片

Vicsek分形体是1983年由英国数学家Vicsek提出的，第1级Vicsek分形由5个同种小正方形的组成，其配置方式是一个小正方形在正方形的中心，4个小正方形分别在正方形的4个角上；第2级的Vicsek分形由5个第1级Vicsek分形组成，其配置方式与第1级Vicsek分形相同，重复构造下去，可以得到所有高级的Vicsek分形(图3).

2.2 实验数据以Koch曲线、Sierpinski三角形垫片、Vicsek分形3种标准分形为研究对象，对本文中的方法进行验证，实验数据如表2.

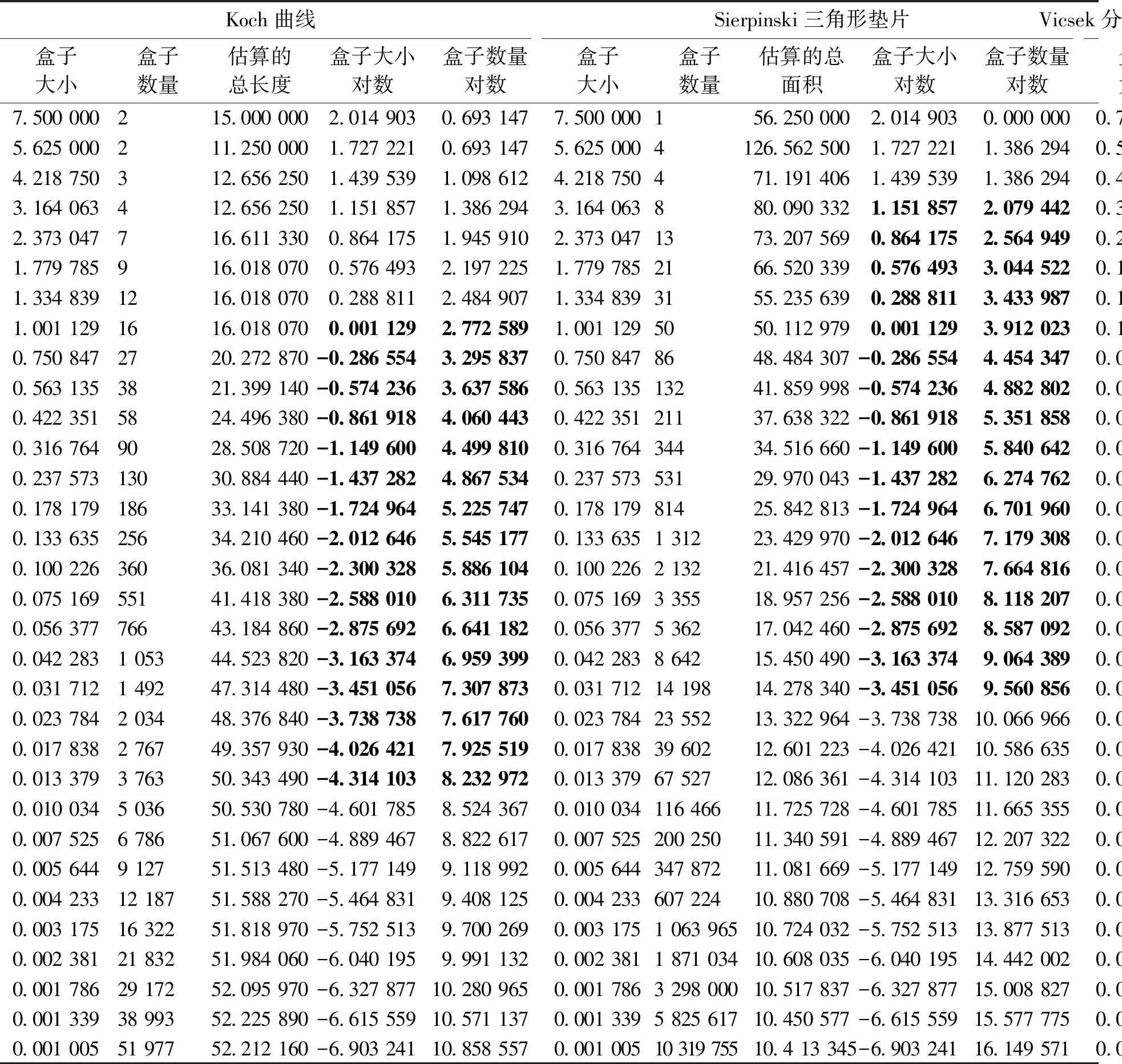
表2 实验数据(加黑数据为有效点对)

图3 Vicsek分形

2.3 实验数据分析当所有点对参与分维估算时，估算的分维值与理论值差异较大(图4、表3)；根据本文中提出的点对剔除方法，当仅有有效点对参与分维估算时，估算的分维值则非常接近分维理论值(图6、表3).这是因为，一方面，测量的前几步由于尺度太大，测量体与分形体吻合不好，测量尺度与相应测度的标度关系不能很好地反映分维数值；另一方面，当测量的尺度足够小时，就会达到分辨率的极限，或者超越分形最小单元的界限，从而尺度与相应测度的标度关系失效.

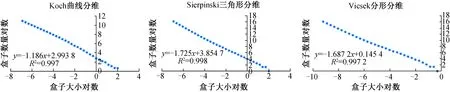
图4 分维(所有点对参与估算)(左：Koch曲线，中：Sierpinski三角形垫片，右：Vicsek分形)

图5 不同盒子测度下估算的总长度或总面积(左：Koch曲线，中：Sierpinski三角形垫片，右：Vicsek分形)(红色点为有效点对)

图6 分维(有效点对参与估算)(左：Koch曲线，中：Sierpinski三角形垫片，右：Vicsek分形)

表3 3种标准分形体的理论和估算分维值

3 结论和讨论

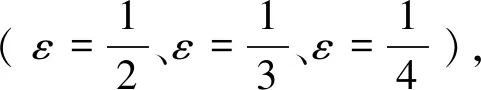
按照上述方法，标度区的判断结果大同小异.实际上，将标度区少算几个观测点原则上不会显著影响分维估算结果.或许准确的分维值很难找到，实际上单独一个分维数值或许没有太多的信息，使用同样方法得到的多个分维值比较才更有意义[7].

计盒维数揭示了研究对象的空间复杂程度、细节多少，或者反映出对平面空间的填充度能力、存在空隙多少等.当D=2.0时，所选范围所有的空隙全部填满，研究目标为欧氏几何图形；当D=0.0时，研究目标集聚成一点.以城市形态为例，在二维空间中，分维通常围绕D=1.7变化，而D大于1.9和小于1.4的城市形态比较罕见[7,12].

任何一个图形都存在一个空间维数(整数维、分数维).把一个复杂图形采用一个数据(分维)来表示，是一个降维问题，一定存在信息丢失，所以存在“异物同维、同维异物”现象.