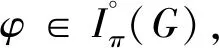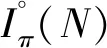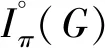π-部分特征标的McKay猜想

2020-06-18常学武王娜

湖北大学学报(自然科学版) 2020年3期

常学武，王娜

(山西大学数学科学学院, 山西太原 030006)

0 引言

设G为任意有限群,p为素数,通常记Irrp′(G)={χ∈Irr(G)|p⫮χ(1)}为G的次数不被p整除的所有不可约复特征标构成的集合.如果P∈Sylp(G)为G的一个Sylowp-子群,则著名的McKay猜想断言|Irrp′(G)|=|Irrp′(NG(P))|.事实上,有限群表示论近50年来的一个主要目标就是证明McKay猜想及其各种变形和加强,至今取得了很多重大的进展和突破,但尚未彻底攻克该猜想,具体成果和相关文献可参考Navarro在2018年出版的最新专著[1],我们在此仅提及几个与本研究有关的经典结果.第一个进展是1973年Isaacs[2]证明了McKay猜想对奇数阶群成立,特别地,他构造了一个典范双射Irrp′(G)→Irrp′(NG(P)).1978年Wolf[3]证明了McKay猜想对任意可解群都成立,而p-可解群的McKay猜想是Dade[4]以及Okushima和Wajima[5]在1979年分别独立地证明的.作为p-可解群的推广,π-可分群的McKay猜想也是成立的,即当G为π-可分群时,设H∈Hallπ(G)为Hallπ-子群,则|Irrπ′(G)|=|Irrπ′(NG(H))|,其中Irrπ′(G)为G的具有π′-次数的所有不可约复特征标的集合.该结果的证明可见Isaacs在2018年出版的最新特征标专著第6章[6].

值得指出的是,在G为可解群时,虽然已证明|Irrp′(G)|=|Irrp′(NG(P))|,但偶数阶可解群G一般不存在从Irrp′(G)到Irrp′(NG(P))的典范双射,一个典型的反例是G=GL(2,3)且p=3.在研究McKay猜想时,一个基本而重要的问题是探讨何时存在典范双射.Isaacs[7]研究M-群的Hall子群时,证明了下述重要结果(即该文中定理B和定理C),意义在于从单项特征标的角度具体构造了McKay猜想中的一个典范双射.

Isaacs定理设G为可解群,π为一个素数集合,H∈Hallπ(G)为G的Hallπ-子群.如果Irrπ′(G)中成员均为单项特征标,则存在一个典范双射

f:Irrπ′(G)→Irrπ′(NG(H))

使得对每个χ∈Irrπ′(G), 只要χ=λG,其中λ∈Irr(U)为线性特征标,并且H≤U≤G,就有f(χ)=(λNU(H))NG(H).特别地,Irrπ′(NG(H))中成员也都是单项特征标.

关于Brauer特征标的McKay猜想,目前已经证明对p-可解群成立,即当G为p-可解群时,则|IBrp′(G)|=|IBrp′(NG(P))|,在此IBrp′(G)表示G的次数不被素数p整除的所有不可约p-Brauer特征标的集合.值得提及的是该结果对非p-可解群一般不成立.此外,Wolf[8]考虑了Isaacs的π-部分特征标,证明了相应的McKay猜想(见该文定理A),包含了上述p-可解群的McKay猜想.这是非常一般化的结果,但Wolf并没有进一步探讨何时两个相应的不可约π-部分特征标(简称为Iπ-特征标)集合存在一个典范双射.关于Iπ-特征标的定义和性质,可见本文中第2节,或参考Isaacs最新特征标著作[6].

本文中主要研究π-部分特征标理论中的McKay猜想,在Wolf工作的基础上(见定理A[8]),我们给出了上述Isaacs定理的π-部分特征标版本,即在π-部分特征标理论的McKay猜想中,具体构造出相应两个Iπ-特征标集合之间的一个典范双射.

定理A设G为π-可分群,H∈Hallπ(G),则存在一个典范双射

f:{φ∈Iπ(G)|φ(1)为π′-数}→{ξ∈Iπ(NG(H))|ξ(1)为π′-数}

使得对任意φ∈Iπ(G)且φ(1)为π′-数,均有f(φ)=(λNU(H))NG(H),其中U为G的子群且包含H,λ∈Iπ(U)为线性特征标,并且φ=λG.特别地,f(φ)不依赖于U和λ的不同选取,并且这两个Iπ-特征标集合中的所有成员均为单项Iπ-特征标.

取π={p}′为素数p的余集,熟知π-可分群即通常的p-可解群,而Iπ-特征标等同于关于素数p的不可约Brauer特征标,即Iπ(G)=IBr(G).下述结果可看成是Brauer特征标中一种“对偶”的McKay猜想,即将Sylowp-子群P∈Sylp(G)替换为一个p-补Q∈Hallp′(G).

推论B设G为p-可解群,Q为G的一个p-补,则存在一个典范双射

f:{φ∈IBr(G)|φ(1)为p-数}→{ξ∈IBr(NG(Q))|ξ(1)为p-数}

使得对任意φ∈IBr(G)且φ(1)为p-数,均有f(φ)=(λNU(Q))NG(Q),其中U为G的子群且包含Q,λ∈IBr(U)为线性特征标,并且φ=λG.特别地,f(φ)不依赖于U和λ的不同选取.此外,上述两个Brauer特征标集合中的所有成员均为Brauer单项特征标.

再取π={p}为素数p的集合,则I{p}简记为Ip,这又是一类很重要的π-部分特征标,可视为关于素数p的Brauer特征标的一种对偶,在M-群和超单项特征标的研究中自然地出现,并提供有效的证明技术,相关文献可见[9-10].下述结果同样可看成是特征标π-理论中McKay猜想的另外一种对偶版本.

推论C设G为p-可解群,P∈Sylp(G),则存在一个典范双射

f:{φ∈Ip(G)|φ(1)为p′-数}→{ξ∈Ip(NG(P))|ξ(1)为p′-数}

使得对任意φ∈Ip(G)且φ(1)为p′-数,均有f(φ)=(λNU(P))NG(P),其中U为G的子群且包含P,λ∈Ip(U)为线性特征标,并且φ=λG.特别地,f(φ)不依赖于U和λ的不同选取,并且上述两个Ip-特征标集合中的成员均为单项Ip-特征标.

本研究只考虑有限群,复特征标的符号和术语可参考Isaacs的两本著作[6,11],关于Brauer特征标可参考Navarro的教材[12].

1 Iπ-特征标及其提升

本节简介所需的π-部分特征标的概念和性质,主要参考文献[6].

设G为π-可分群,通常记G0为G的所有π-元素构成的集合,则G的每个复特征标χ∈Char(G)在G0上的限制χ0称G的一个π-部分特征标.如果G的π-部分特征标χ0不能表为两个π-部分特征标之和,即不存在χ0=φ0+ψ0,其中φ,ψ为G的复特征标,则称χ0为G的一个不可约π-部分特征标,简称为G的Iπ-特征标,G的全体不可约π-部分特征标的集合记为Iπ(G).关于π-部分特征标到子群的限制和从子群的诱导,可按通常复特征标的限制和诱导定义.设H≤G,θ∈Char(H)且χ∈Char(G),则定义(χ0)H=(χH)0和(θ0)G=(θG)0.

从定义不难看出:当π={p}′为素数p的余集且G为p-可解群时,根据模表示论中著名的Fong-Swan定理,可知π-部分特征标即通常关于素数p的Brauer特征标,而Iπ-特征标等同于关于素数p的不可约Brauer特征标,亦即Iπ(G)=IBr(G),表明Iπ-特征标恰为不可约Brauer特征标在π-可分群中的直接推广.

为了研究π-部分特征标理论, Isaacs采用了类似于Fong-Swan定理给出的提升技术,核心内容是定义了所谓Bπ-特征标集合Bπ(G)⊆Irr(G),作为Iπ(G)的一种典范提升,即特征标的π-限制χ|→χ0给出了一个典范双射:Bπ(G)→Iπ(G).但Bπ-特征标的定义相当复杂,难以在此精确地给出,并且通常判定一个不可约复特征标χ∈Irr(G)是否为Bπ-特征标,也是很困难的问题.在2∈π的情形, Isaacs定义了一个关于群G和素数集合π的域自同构τ,可用来简单地判别Bπ-特征标,具体内容可见文献[6].

引理1.1设G为π-可分群, 2∈π,并且τ为关于G和π的域自同构.如果χ∈Irr(G),则χ∈Bπ(G)当且仅当χτ=χ且χ0∈Iπ(G).

引理1.1的证明见定理5.2[6].

但在2∉π的情形,则上述Bπ-特征标的判别方法失效,并且此时Bπ-特征标的诱导和限制等过程均难以控制.为此Isaacs[9，13]又定义了Dπ-特征标,同样指定了一个子集Dπ(G)⊆Irr(G),作为Iπ-特征标在2∉π时的又一种典范提升,即特征标的π-限制χ|→χ0也是一个双射:Dπ(G)→Iπ(G).值得指出的是Bπ-特征标和Dπ-特征标一般是不同的,但在奇数阶群中这两类特征标是一致的.

事实上,Dπ-特征标的定义同样很复杂的,特别是涉及到子群H在G中所谓的π-标准符号特征标δ(G,H),属于一类取值为±1的特殊的线性特征标.此外,如果θ∈Char(H),则定义θ到G的π-诱导θπG=(δ(G,H)θ)G.相关概念和性质,均可参考文献[6]或上段提及的两篇文献.

我们需要判别特征标的π-诱导何时恰为通常诱导,下述即为所需的一个充分条件.

引理1.2设G为π-可分群且2∉π,J≤G使得|G:J|为π′-数.如果α∈Char(J)为J的一个复特征标,则απG=αG.

引理1.2的证明因为|G:J|为π′-数,从定理2.5[13]可知J在G中的π-标准符号特征标δ(G,J)=1J,再从特征标π-诱导的定义得到απG=(δ(G,J)α)G=αG.

下述是Dπ-特征标的判别定理,即著名的Dade定理.

引理1.3设G为π-可分群且2∉π,如果H≤G,θ∈Irr(H)和χ∈Irr(G),满足θπG=χ,则θ∈Dπ(H)当且仅当χ∈Dπ(G).

引理1.3的证明见定理E[9].

通常在研究Iπ-特征标时,考虑到Bπ-特征标和Dπ-特征标各自具有的技术便利,人们往往区分两种情形,即2∈π和2∉π.方便起见,我们引入一个概念.

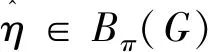
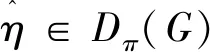
在本文中主要定理的证明中,我们将使用上述标准提升技术,把Iπ-特征标的结果提升为复特征标的相应结果,再借助Isaacs定理完成证明.为此,我们还需要用到Isaacs[7]的一个基本引理.

引理1.5设G为任意群,H∈Hallπ(G),U,V≤G，H≤U∩V,λ∈Irr(U)和μ∈Irr(V)均为线性特征标,使得λG,μG∈Irr(G).令N=NG(H).如果(λU∩N)N=(μV∩N)N则λG=μG.

引理1.5的证明即引理2.3[13]的特例.

最后,本文中还要用到下述Wolf定理,内容证明了Iπ-特征标的McKay猜想.

引理1.6设G为π-可分群,H∈Hallπ(G),则下述两个Iπ-特征标的集合具有相同的基数:

|{φ∈Iπ(G)|φ(1)为π′-数}|=|{ξ∈Iπ(NG(H))|ξ(1)为π′-数}|.

引理1.6的证明属于定理A[8]的特例,取其中素数集合ω=π即可.

2 主要结果及证明

我们先建立一个基本结果,在定理A的证明中有重要作用.

定理2.1设G为π-可分群,H∈Hallπ(G),并且φ∈Iπ(G).如果φ(1)为π′-数,则存在G的子群U≥H以及线性Iπ-特征标λ∈Iπ(U)使得φ=λG.进而,对任意如此的子群U和线性Iπ-特征标λ,均有(λNU(H))NG(H)不可约.

定理2.1的证明根据Iπ-特征标的Huppert定理(见推论5.5[6]),则Iπ-特征标存在π-次诱导,即存在子群U≤G以及λ∈Iπ(U)，使得φ=λG且λ(1)为π-数.此时φ(1)=|G:U|λ(1),已知φ(1)为π′-数,故|G:U|和λ(1)均为π′-数.由此可知λ(1)=1,即λ为线性的Iπ-特征标,并且U包含G的Hallπ-子群,从G为π-可分群可知其所有的Hallπ-子群彼此共轭,故H包含在U的某个G-共轭Ug中.此时(Ug,λg)也是φ的一个π-次诱导对,满足H≤Ug且λg(1)=λ(1)=1.我们用(Ug,λg)替换(U,λ)，即得所需的子群U和线性特征标λ.

固定任意一个Iπ-特征标对(U,λ)满足所述条件,为了便于归纳,我们将证明一个稍微一般的结论:只要子群J≤G使得|U:U∩J|为π′-数,就有(λU∩J)J∈Iπ(J).通过取J=NG(H),则U∩J=NU(H)≥H,显然满足指数为π′-数的条件,故得所证结论(λNU(H))NG(H)不可约.为此,我们将用反证法,假设(λJ∩U)J是可约的,在所有反例中,我们依次选取|G|, |G:U|和|G:J|尽可能的小,分以下几步完成证明.

1) 我们断言J必为G的极大子群.事实上,如果J不是极大子群,则存在中间子群V使得J

2) 任取N◁G,只要N≤U∩J,我们将证明φN必然是齐次的,即仅有唯一的Iπ-分量.为此,选取θ∈Iπ(N)在λ∈Iπ(U)的下方,因为λ是线性的Iπ-特征标,故λN=θ.特别地,θ是U-不变的.令T=IG(θ)为θ在G中的惯性群,则U≤T. 假设φN不是齐次的,因为θ也是φN的不可约分量,故φN非齐次等价于θ不是G-不变的,即T

3) 我们证明φJ是可约的.如果φJ不可约,则(λG)J=φJ∈Iπ(J),任取μ∈Irr(U)为λ∈Iπ(U)的提升,即μ0=λ,则((μG)J)0=((μ0)G)J=(λG)J=φJ不可约,迫使复特征标(μG)J也不可约,由Mackey定理可知G=UJ.此时(μU∩J)J=(μG)J,两边再做π-限制得到

(λU∩J)J=((μ0)U∩J)J=((μU∩J)J)0=((μG)J)0=((μ0)G)J=φJ∈Iπ(J),

与极小反例的假设矛盾,故φJ是可约的.

4) 因为φ不能是线性特征标,否则U=G且λ=φ,而U∩J=J,此时λJ∈Iπ(J),结论成立,与极小反例矛盾.已知φ(1)是π′-数,故φ(1)不能是π-数.使用引理5.12[6],存在某个G的正规子群M,使得φM的任意不可约分量γ的次数均为π-数,但γ不是G-不变的,等价于φM不是齐次的.因为φ=λG从U诱导,再由引理5.21[6]可知|MU:U|为π-数.但|G:U|整除φ(1)为π′-数,迫使MU=U,即M≤U.

如果M⊆J,从J为极大子群可知G=MJ,从而|M:M∩J|为π′-数.此时M∩J包含M的一个Hallπ-子群,仍从引理5.14[6]推出φM的不可约分量γ在M∩J上的限制不可约.此时φ∈Iπ(G|γ),再根据引理5.20[6],可知φJ也不可约,又与(3)中结论矛盾,故M≤J.

至此即证M≤U∩J,但M◁G且φM不是齐次的,又与2)中结论矛盾,证毕.