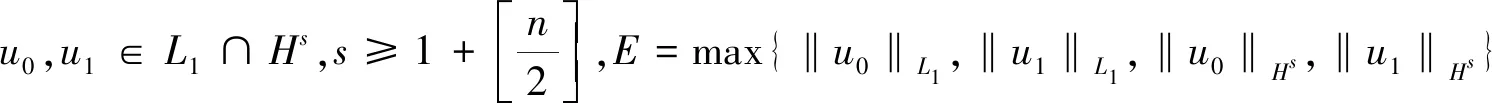带内能的Cahn-Hilliard方程解的整体存在性

徐红梅，李奇

(河海大学理学院, 江苏 南京 211100)

0 引言

研究在空间维数为1≤n≤3时带内能的Cahn-Hilliard方程在小初值情况下经典解的整体存在性:

(1)

其中，η>0是一个给定的常数，u表示一相对浓度.在非线性项Δf(u)中,取f(u)=u2.当η=0时,(1)式就是著名的Cahn-Hilliard方程[1].

ut+Δ2u-Δf(u)=0， (x,t)∈Rn×(0,∞)

(2)

为模拟在某些玻璃中由于过深过冷引起的不平衡分解,Galenko等[2-4]提议在方程(2)中增加不活泼项ηutt,即方程(1)式,详细物理背景可参看文献[3-4].

Cahn-Hilliard方程是抛物方程,因其丰富的物理背景,已有许多研究[5-9],但(1)式是一个带松弛项的双曲型方程,它的解在有限时间内不再正则化,因此很难得到经典解的整体存在性.事实上,对于(1)式,之前的工作主要集中在能量有界解和拟强解上[10-11].如文献[10]指出,(1)式是与半线性波动方程有很多相似之处,但由于它的弱耗散性,我们很难仅用标准能量方法得到(1)式解的整体存在性.Wang和Wu[12]介绍了一个长短波的方法,他们分别用格林函数和能量估计的方法来估计低频和高频部分,从而得到了(1)式在n≥3时小初值情形经典解的整体存在性.空间维数大小在衰减估计中起着很重要的作用.维数越高,衰减速度越快.本研究通过构造一个完备度量空间的柯西序列的方法得到了(1)式在小初值情况下经典解的整体存在性.在证明是柯西序列的过程中,我们同样分高低频用不同方法作估计.在高频时,我们是通过对格林函数的详细分析取代文献[12]中的能量估计得到的.

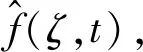
1 柯西序列的构造

令u(m)是下列线性非齐次方程的解

(3)

其中m≥1.且令u(0)(x,t)=0.由齐次化原理，类似文献[12]中2.5式的方法，得到(3)式的解为

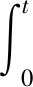
(4)

其中G是下列线性齐次方程的解

其中δ(x)为Dirac函数.容易算出

(5)

其中

(6)

我们首先分高低频对G(x,t)作出估计.先作光滑截断函数

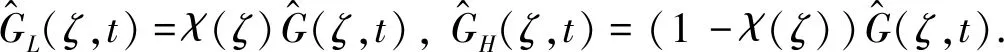
定理1对任意多重指标α,存在依赖于α的常数Cα,有

(7)

(8)

所以

(9)

因为

I1+I2+I3

(10)

由(6)～(9)式得

(11)

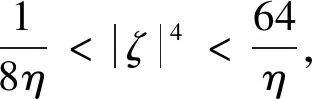
(12)

由(10)～(12)式,定理得证.

因为

(13)

定理2当u∈Hs,对任意α,|α|≤s,有

定理2的证明当4η|ζ|4≥2,由(6)式，有

所以

定理3的证明证明分3步.

1)u(0)(x,t)=0∈Ds,E.

2) 若u(m-1)(x,t)∈Ds,E,要证u(m)(x,t)∈Ds,E,由定理1,定理2,得

CE

(14)

由定理1,定理2,引理3.2[12]及Sobolev不等式,得

CE2+CE2

(15)

由(14)～(15)、(4)式,当E<1,有u(m)(x,t)∈Ds,E.

3) 证u(m)(x,t)是Ds,E内的柯西列.

令v(m)(x,t)=u(m)(x,t)-u(m-1)(x,t)，m≥3.

由(3)式,得v(m)(x,t)是下列方程的解.

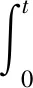
由定理1，定理2，引理3.3[12],当|α|≤s,得

CE‖v(m-1)‖L∞(0,+∞;Hs(Rn))+CE‖v(m-1)‖L∞(0,+∞;Hs(Rn))=

2CE‖v(m-1)‖L∞(0,+∞;Hs(Rn)).

则u(m)(x,t)是Ds,E内的柯西列.

综合步骤1)-3)定理得证.

2 结论

由于Ds,E是完备度量空间,由u(m)(x,t)的构造方法，得到本文中结论.