不同车辆密度下的车联网最大路由跳数仿真研究*

裴忠惠 杜路遥 纪 军 陈 伟，▲ 郑洪江

（1.武汉理工大学信息工程学院 武汉 430070；

（2.武汉理工大学自动化学院 武汉 430070；

（3.上海智能网联车载终端工程技术研究中心 上海 200030；

（4.上海博泰悦臻电子设备制造有限公司 上海 200030）

0 引 言

近年来，随着智能交通系统（intelligent transportation system，ITS）和自动驾驶技术的快速发展，车联网（internet of vehicles，IoV）作为其中的关键部分也得到了人们的重要关注，国内提出的智能网联汽车概念将车联网与智能车技术结合，使得车与路能够更好的协同工作[1-2]。车联网能够实现车与车（Vehicle to Vehicle，V2V）、车与路侧单元（Vehicle to Infrastructure，V2I）的实时可靠通信，为智能交通和车路协同提供了网络通信基础[3-5]。

由于车辆节点快速移动的特性，车联网的网络拓扑存在高动态地变化特性，传统网络中的路由技术大多不能够在这样高动态的网络环境中保证良好的通信质量[6-7]。针对车联网的高动态特性以及实际应用中的网络要求，众多路由方案被提出。根据路由技术所需的信息[8]，可分为基于网络拓扑的路由协议，例如无线自组网按需平面距离向量路由协议(ad-hoc on demand distance vector AODV)；基于地理位置的路由协议，例如贪婪边界无状态路由协议(greedy perimeter stateless routing GPSR)；基于地图的路由协议，例如地理源路由(geographic source routing GSR)；以及基于路径的路由协议，例如车辆辅助传输路由(vehicle-assisted data delivery VADD)[9]。

在各种路由协议中，路由跳数是一个极为重要的参数，与链路连接性、链路可靠性及数据包投递率有着密切联系，而在车联网这样一个高动态多变的网络环境中，其重要性尤为突出。通常不同的路由协议有其各自的路由跳数选择优化方案，AODV路由协议中是从可选的路由路径中选择路由跳数最小的1条路径进行转发，VADD选择具有最低延时的转发路径。赵海涛等[10]提出一种基于连通概率感知的多跳消息转发算法，利用所建立的多车道多跳连通概率分析模型，选择连通概率较高的道路路段和车辆节点进行转发。张沪寅等[11]结合了有限频谱资源调度研究与最小化路由跳数的优化目标，提出一种认知无线车载自组织网络中的联合路由调度，通过车辆间有效接触时间和CR频谱可用概率定义通信链路消耗，并提出一种混合启发式算法，对有限频谱资源进行调度，同时优化路由跳数。M.Nabil等[12]利用车辆位置信息、行驶方向和邻居车辆预计停留时间改进了位置辅助路由 (LAR),以增加路由生存时间。N.S.Rajput等[13]综合网络的时间、空间和环境依赖性进行链路鲁棒性地建模和量化，并在此基础上提出了一种路由选择策略。

目前针对车联网路由跳数的研究大多为最优化路由选择方案，以最小化路由跳数、最大化路由生存时间或者综合考虑多项通信性能指标来决定最终路由路径选择，但是却较少针对最大路由跳数参数的选择进行研究。最大路由跳数参数的设置限制了路由数据包的生命周期，决定着路由路径所经过的中继节点的最大跳数。值得注意的是，即使拥有较优的路由路径选择策略，最大路由跳数的设置依然对网络有着较大的影响，过大的数值可能会过度增加路由开销，增加网络拥堵，降低网络的数据传输率及可靠性；过小的数值又会导致路由成功率降低，同样会降低网络的数据传输率及可靠性[14-15]。

车辆密度对于车联网网络的连通性及各项通信性能有着重要的影响，将道路交通条件与网络环境相结合能够更好的发挥智能网联与车路协同的优势，形成环境与网路的自适应交互。Q.Yang等[14]在中提出一种自适应连接感知路由协议（ACAR），通过统计车辆密度和实时车辆密度收集以及文中建立的连接性模型来优化路由转发策略，以最小化分组错误率。O.S.Oubbati等[16]提出了在城市车载环境中使用实时交通信息的智能路由协议(IRTIV)，通过周期性的hello消息来收集实时的交通密度并基于交通密度和Dijkstra算法计算路段的权重，选择具有足够车辆连接和最短的传输路径，但是在交通密度较低时很难找到转发路径。C.Wang等[17]提出了一种用于车联网的软件定义认知路由(SDCoR)，利用软件定义网络和强化学习对环境进行感知学习，文中用到了车辆密度和速度2个环境参数，并设计了基于Q-learning的感知路由算法根据不同的环境来选择不同的路由策略。

一般来说，在车辆密度较大的环境下，节点之间的连通概率较大，但同时节点密度过大也容易导致网络拥堵现象，相反，在车辆密度较小时，发生网络拥堵的概率较低，但是节点之间的连通性也会随之降低[18]。将最大路由跳数参数与车辆密度相关联，利用道路交通条件优化网络建设，研究在不同的车辆密度情况下，选择不同的最大路由跳数参数对网络各项性能指标的影响，包括理论分析与仿真研究，为网络与环境的智能交互提供理论基础。

1 多跳车联网系统架构

车联网作为一个高动态大型网络，包括通信车辆和路边基础设施（roadside units，RSU）2个通信主体，通信方式包括车对车通信和车对基础设施通信。目前车联网的通信标准大多为单跳通信，在简化网络拓扑的同时，也降低了网络资源的利用率，增加了网络建设的成本，多跳通信是车联网发展的一个必然趋势。

多跳车联网系统架构见图1，路侧单元也可以看作是1个小型的通信基站，车辆可以看作是数量众多的移动通信终端。图1中r为车辆的有效通信半径（单位：m），RSU的通信范围通常由于其较大的功率会覆盖更大，用R表示（单位：m）。车联网中多跳通信的优势体现在2个方面：①针对V2I通信，对于RSU的布设来说，如果仅允许单跳通信，那么其布设密度要求较高，2个RSU之间必须无缝衔接，这样才能保证所有车辆均覆盖在RSU的有效通讯范围内。但是如果允许多跳通信，RSU的布设密度可以相对减小，例如图1中RSU1与RSU2可以不相互覆盖，转而通过它们之间车辆的多跳通信来间接增加其自身的覆盖范围。②对于V2V通信而言，例如图1中的车辆节点Vs与Vd如果想完成直接通信，仅通过单跳通信方式显然无法实现，而通过多跳通信则可实现。

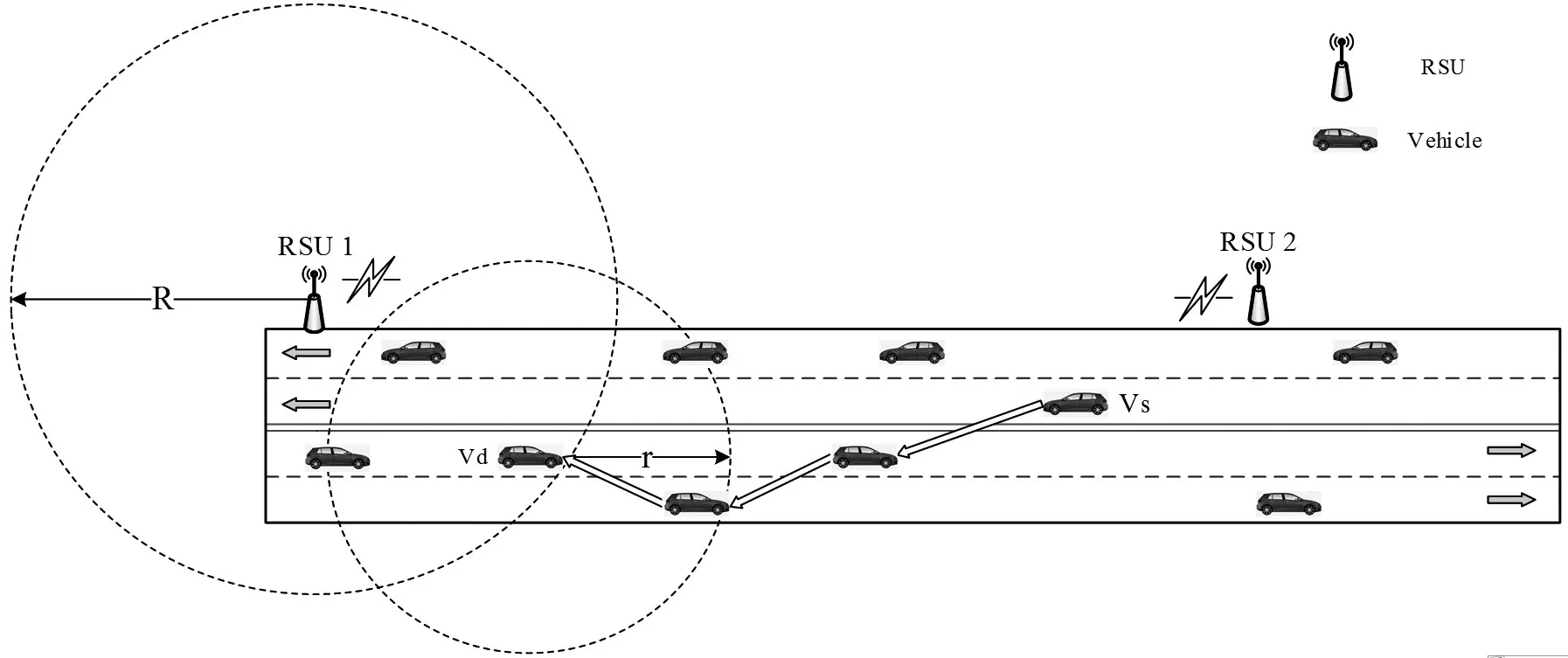
图1 多跳车联网系统架构Fig.1 Multi-hop IoV system architecture.

多跳车联网在一定程度上可以增加网络资源的利用率，减少网络的布设成本，但是如果网络中的跳数过大，同样会导致网络通信冲突增加，造成广播风暴，降低网络的吞吐量，所以对车联网最大允许路由跳数的设置至关重要。固定的最大路由跳数通常不能适应车联网环境的复杂多变，利用车路协同思想根据不同的交通车辆密度设定对应的最大路由跳数，可以改善车联网的多跳通信性能，做到真正的智能网联。

2 节点连接性概率及数据包投递率模型与分析

在车联网中通信质量的评估可以使用多种度量方式，针对网络节点间的最大路由跳数参数和车辆密度与节点连接概率和包投递率之间的联系进行理论模型分析。

2.1 节点连接性概率模型与分析

设车辆的通信模型为Unit-disk模型，这是最简易的一种通信模型，即假定车辆的有效通信半径为R，则只要2车之间的距离小于R即可建立有效通信。设g(x)为2节点之间可以建立通信的概率，则

式中：x为2个节点之间的距离，m。

考虑一种特殊场景下的节点连接概率与最大路由跳数及车辆密度的关系，见图2，设车辆在长为Lm的直线路段中，源节点车辆Vs与目的节点车辆Vd距离为 x,m，车辆通信范围为 R,m，且R＜x＜2R。

由图2中的场景可以看出，增加路由跳数可以在一定程度上增加节点之间的连接性概率，例如，源节点车辆Vs需要与目的节点车辆Vd建立通信链路，在最大路由跳数设置为1时，由于车辆间距x＞R，2个节点之间无法建立通信。最大路由跳数设置为2时，源节点与目的节点之间可以建立1条可能的通信链路Vs→Va→Vd。将最大路由跳数设置为3时，源节点与目的节点之间可以建立4条可能的通信链路，其中1条可能链路为2跳通信：Vs→Va→Vd；另外3条可能的通信链路为3跳通信：Vs→Va→Vc→Vd，Vs→Vb→Va→Vd，Vs→Vb→Vc→Vd。

图2 特殊场景下的车辆坐标图Fig.2 Vehicle coordinates in specific scenario

以源节点Vs为坐标原点建立一维坐标系，由于道路宽度相对于车辆通讯距离来说较小，故忽略道路宽度对通信距离的影响。在R＜x＜2R的场景下，分析最大路由跳数及车辆密度对节点之间的连接性概率的影响。

实际应用中的车辆密度通常由道路传感器检测、历史交通流密度记录和车联网通信中的beacon消息等方式获取，此处为便于分析，假设车流量分布服从车辆密度为λ辆/m的泊松分布[19]，则有k辆车分布在长度为x的路段上的概率为

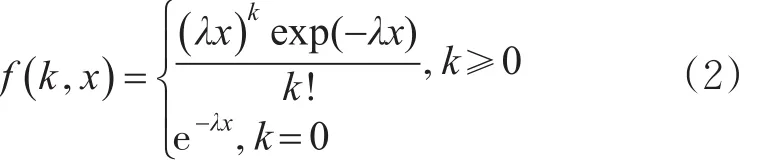
式中：e为自然指数。根据泊松分布模型，在长度为Lm的路段上共有车辆λL辆，其中源节点与目的节点之间共有车辆λx辆。设K(R)为长度为R的路段内存在的车辆数量，则R范围内至少有1辆车的概率为

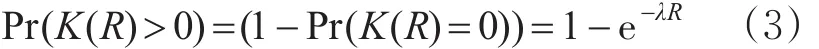
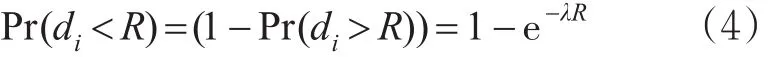
设h为通信链路的路由跳数，f(h=i)为路由跳数等于i时源节点Vs与目的节点Vd的连接性概率，xi为第i跳中继节点的坐标位置，即第i跳节点与Vs之间的距离，且 xi＜x,则设H为节点所允许的最大路由跳数，P(H=j)为最大路由跳数参数等于 j时源节点Vs与目的节点Vd的连接性概率，则

由于研究内容是最大路由跳数参数H对节点网络层的连接性概率的影响，故可假设在一般场景下（即在任意长度的路段，2个相距任意距离的源节点与目的节点），f*(h=i)为路由跳数等于i时源节点与目的节点的可能连接概率，P*(H=j)为最大路由跳数参数等于 j时源节点与目的节点的连接性概率，则

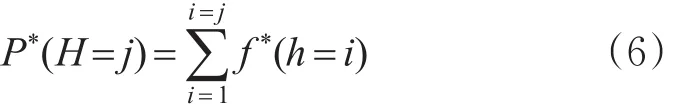
通过所建立的最大路由跳数和车辆密度的节点连接性概率数学模型不难看出，所允许的最大路由跳数和车辆密度越大，则节点之间的连接概率越大。

2.2 数据包投递率模型与分析

包投递率是指网络中成功接收的数据包的总数量与发送的数据包总数量的比值，能够直观地反映网络通信质量。数据包传输失败的原因主要分为2个：数据碰撞和物理层数据错误。首先提出路由跳数和车辆密度与网络层数据碰撞率的关系模型，然后结合物理层的传播模型共同建立了路由跳数和车联密度的数据包投递率模型。

设每个车辆节点在1个数据包持续时间内发送数据包的平均概率为τ，则

式中：Smean为数据包的平均持续时间，s，根据数据包长度获得；Tmean为数据包平均发送间隔，s；Hmean为平均最大路由跳数。

另节点干扰范围为R，则范围R内同1个数据包持续时间不发生碰撞的概率Pn为

则单跳碰撞概率Pc=1-Pn，h跳碰撞概率为

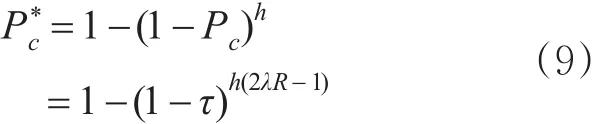
由于本文针对包投递率模型的研究主要为网络层最大路由跳数对其造成的影响，并且路由跳数的变化与物理层信道无关，故此处不对信道模型做研究。假设在DSRC/IEEE 802.11p物理环境下的信噪比为SINR，且使用BPSK调制方式，由文献[14]，其位错误率（Bit Error Rate,BER）可表示为

式中：N为重传次数。假设每个数据包由t帧组成，则物理层传输单跳数据包错误率PERphy=1-那么对于跳数为h的路由链路来说，其物理层传输数据包错误率为

由此，同时考虑数据碰撞率及物理层传输的数据包错误率，则数据包投递率可以表示为

通过以上建立的车辆密度和最大路由跳数的节点连接性概率模型和数据包投递率模型可以较为直观地反映车辆密度和最大路由跳数对通信质量的影响以及最大路由跳数与车辆密度之间的联系。大的路由跳数和高的车辆密度均可以增加节点间的连接概率，同时也会增加数据包的传输失败率，由此可以针对不同的车辆密度设置不同的最大路由跳数，达到车路智能交互的目的，并为进一步优化车联网路由算法提供了理论基础。

3 仿真实验与结果分析

使用Veins仿真平台，利用AODV路由协议，分析在不同车辆密度下，不同的最大路由跳数参数选择对网络的各项性能指标的影响。

3.1 仿真环境设置

Veins仿真平台集成了OMNET++网络模拟器及SUMO道路交通模拟器，为车联网地仿真提供了一套开源的仿真架构[20]。由于直线道路上的车辆密度分布简单，能够直观地反映不同的车辆密度下的最大路由跳数参数对通信指标的影响，首先建立1段长为5 km的直线道路仿真场景，双向4车道，也可用来代表高速公路场景。然后将仿真实验扩展到一般城市场景，对2 500 m×2 500 m的城市道路区域进行实时仿真数据分析。笔者重点关注于在同一道路环境下最大路由跳数及车辆密度对通信指标造成的影响，对直道场景与城市道路场景的环境差异可在进一步的工作中展开深入研究。

为了模拟真实的车辆模型，在SUMO环境下设置4种不同的车辆类型（根据市场上典型车辆数据），包括对车辆的最大速度、车辆加速度、车辆减速度、车辆长度及跟车模型等参数的设置，见表1，其中类型A为默认类型。同时使用Krauss跟车模型及LC2013变道模型，其中sigma为跟车模型的驾驶员行为因子。车辆以每秒钟给定的概率随机生成，并且从不同的道路位置以随机速度进入道路。利用对车辆生成概率的设置，可以粗略地控制车辆的分布密度，并且生成的车辆大致服从泊松分布模型。

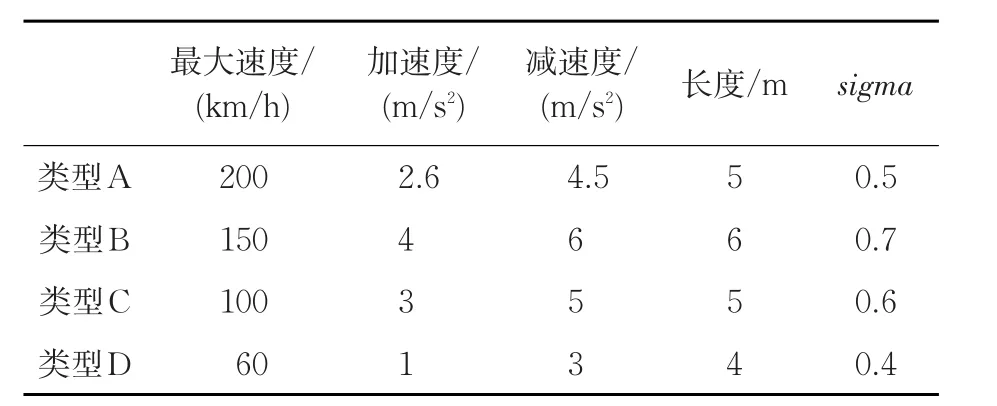
表1 4种车辆类型参数Table.1 Four Vehicle Types with Different Parameters

网络应用层使用UdpApp，车辆进入道路后以0～5 s的随机时间进行周期地发送信息，传输目的地址从道路中已有的车辆节点中进行随机选择，每个数据包的长度设置为512 Byte。为了实现可重复的随机性实验研究，同一场景下的同一组数据使用相同的随机数种子，并将几组不同随机数种子的数据取均值作为最终仿真数据。网络层使用IPV4报文格式，并且使用AODV路由协议。MAC层和物理层使用802.11p标准，每个节点的有效通信范围设置为300 m。每次仿真运行的时间根据道路长度和车流密度设置为300～600 s，通过不同仿真情景下的包投递率、路由跳数和端到端延迟来评价网络的通信性能。

3.2 仿真结果分析

3.2.1 直道场景

通过控制每个车道的车辆生成率λ（每秒钟生成车辆的概率，取值0～1）来控制车辆的分布密度，每组仿真运行时间为300 s，统计在不同的车辆密度情况下，不同的最大路由跳数参数的选择对网络的平均包投递率、平均路由跳数和平均端到端延时的影响。在整个仿真过程中，当λ=1时，道路上平均存在的车辆数量为71辆；λ=0.6时，平均存在车辆46辆；λ=0.2时，平均存在车辆20辆。

由图3可见，在最大路由跳数设置为10及以下时，随着车辆生成率的增加，包投递率也会随之增加，但是当最大路由跳数设置为15及以上时，车辆生成率由0.2升至0.6时包投递率随之增加，而由0.6升至1时导致了包投递率的降低。这说明在最大路由跳数参数数值较小时，高的车辆密度会增加数据包投递率，但是当最大路由跳数参数较大时，存在1个车辆密度的阈值。当车辆密度低于这个阈值时，包投递率会随着车辆密度的增加而增加；但是当车辆密度高于这个阈值时，数据包投递率会随着车辆密度的增加而降低，因为过大的路由跳数和车辆密度导致了严重的网络拥堵。

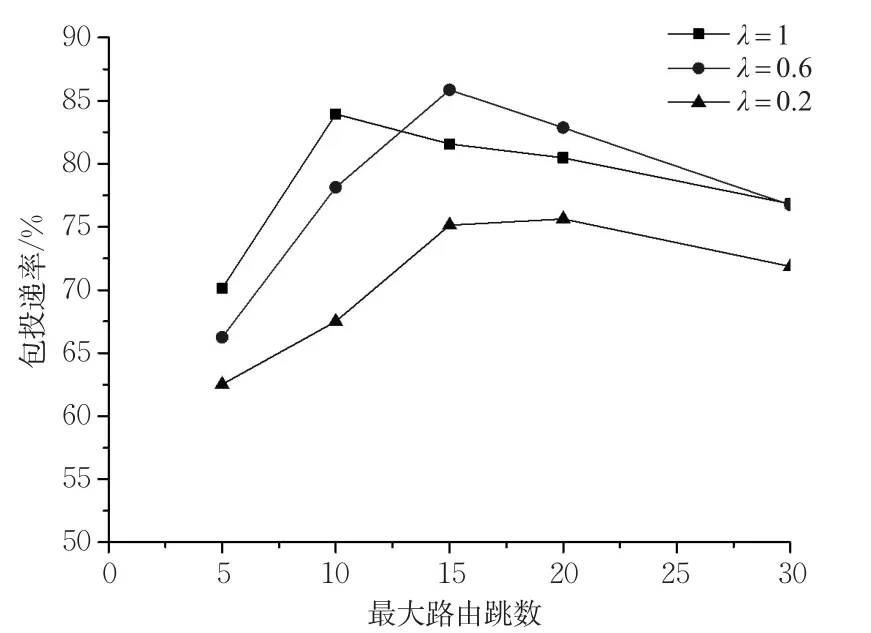
图3 不同车辆密度和最大路由跳数下的包投递率Fig.3 Packet delivery ratio with different vehicle density and maximum routing hops

还可以观察到，在车辆生成率一定时，存在1个最大路由跳数的阈值，当最大路由跳数的数值低于这个阈值时，增加最大路由跳数的数值会增加数据包投递率，但是当最大路由跳数的数值高于这个阈值时，增加最大路由跳数的数值会降低数据包投递率。同时，在车辆生成率一定时，实验中选择不同最大路由跳数造成的包投递率差异最大可达约20%，且存在一个最佳的最大路由跳数参数使得平均包投递率最高（例如车辆生成率为0.6时，最佳的最大路由跳数值为15），并且越小的车辆生成率通常对应于越大的最大路由跳数最佳数值，这表明可以根据不同的车辆密度来选择最佳的最大路由跳数参数。

图4给出了不同车辆密度和最大路由跳数下接收到的数据包的平均路由跳数。总体来说，增加最大路由跳数的数值会使平均路由跳数增加，但是当最大路由跳数和车辆密度均处于较大值时，增加最大路由跳数的值对平均路由跳数的增加影响不大，甚至会出现较小幅度的减小。这是因为在这种状态下网络拥堵情况严重，且丢包率会随着路由跳数的增加而增加，故虽然增加了允许的最大路由跳数，但实际上完成较大路由跳数传输的数据包很少，这种现象在实时仿真过程中很容易观察到。另外，在最大路由跳数一定时，随着车辆密度的增加，平均路由跳数总体呈现增加的趋势，因为车辆密度的增加会增加节点间的连接概率，为更大的路由跳数提供了可能性。

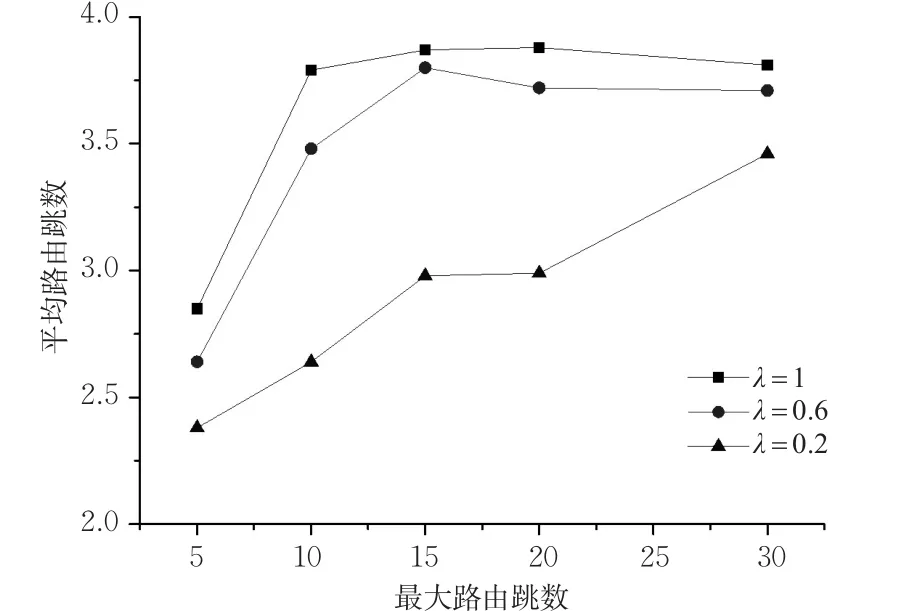
图4 不同车辆密度和最大路由跳数下的平均路由跳数Fig.4 Average routing hops with different vehicle density and maximum routing hops

从图5可以看出，随着最大路由跳数数值的增加，平均端到端延时也会随之增加。这是因为我们在仿真过程中计算的端到端延时为数据包生成的时间到被目的节点成功接收此数据包的时间，而当最大路由跳数增加时，AODV路由过程中的可选路径增加，同时路由过程中的路由请求（Route Request，RREQ）和路由回复（Route Reply，RREP）数据包也会增加，进而增加了路由过程中的决策时间。并且平均路由跳数的增加也会增加一定的数据包端到端延时。

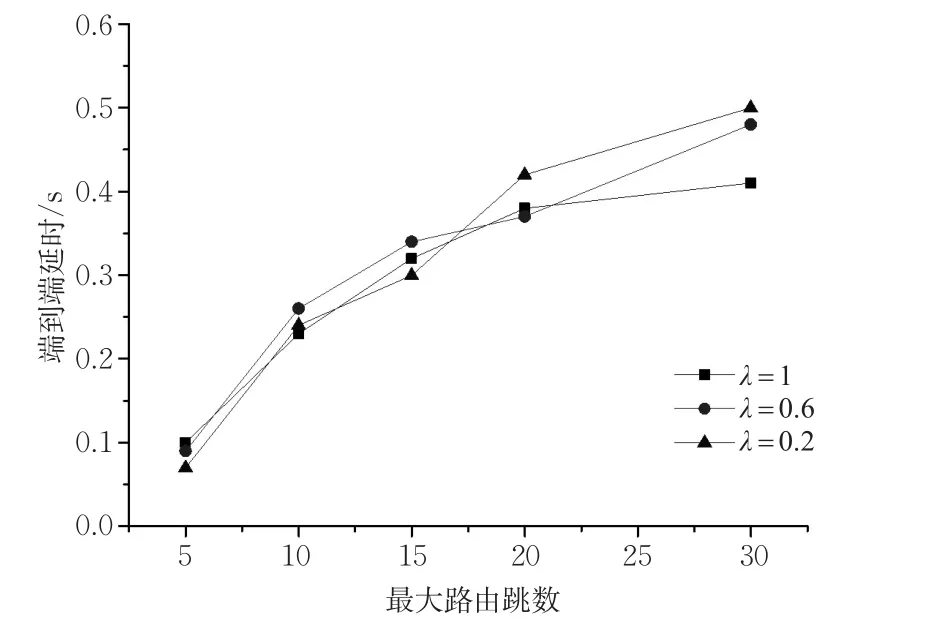
图5 不同车辆密度和最大路由跳数下的端到端延时Fig.5 End to end delay with different vehicle density and maximum routing hops

3.2.2 城市道路场景

为将研究扩展到一般场景，选择2 500 m×2 500 m的城市道路区域进行实时仿真数据分析，包括红绿灯、建筑物等道路环境地设置，仿真时间为600 s。

图6为仿真过程中记录的道路中实时存在的车辆数量，图7为实时仿真过程中设置不同的最大路由跳数参数对应的包投递率，可观察不同仿真时间道路中存在车辆的数量对应的包投递率。为便于观察，我们对仿真过程中数量过大的包投递率数据做了窗口平均和指数加权平均处理。可以看出，在约180 s之前，即道路中的车辆数量约低于85辆时，最大路由跳数参数越大，数据包投递率越大；而在180 s之后，即道路中的车辆数量约高于85辆时，最大路由跳数参数越小，数据包投递率越大。

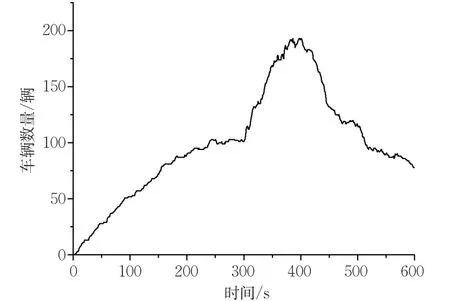
图6 实时车辆数量Fig.6 Number of vehicles in real-time

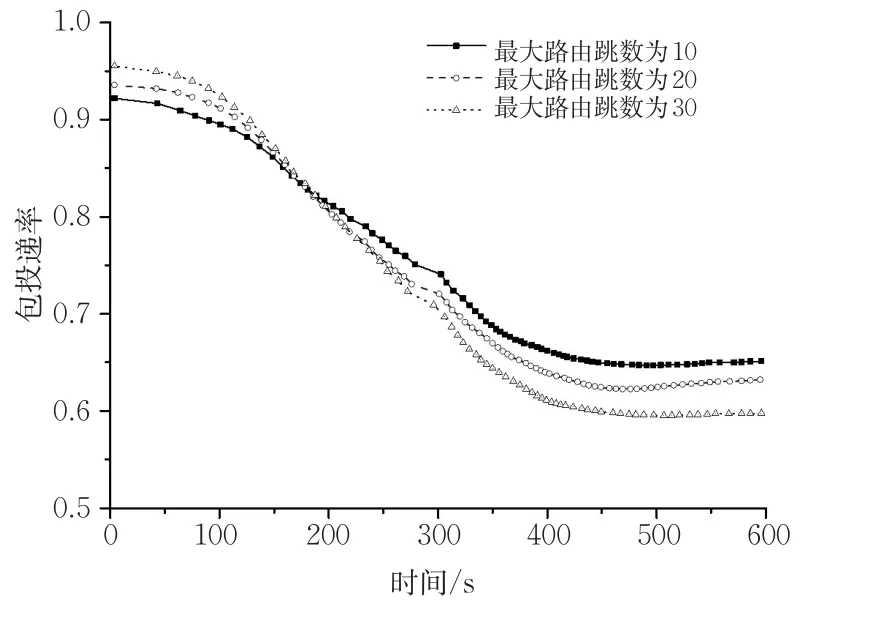
图7 实时数据包投递率Fig.7 Packet delivery ratio in real-time

图8 和图9分别列出了城市道路场景仿真过程中的实时路由跳数和端到端延迟，由于实际数据量过大，图中显示的数据已经过窗口平均和指数加权平均处理。可以看到，在仿真开始约200 s前，由于车辆密度较小，最大路由跳数设置越大，实时路由跳数越大；在200 s之后随着车辆密度的增加，最大路由跳数为30时的实时路由跳数低于其他2组数据；在约250～450 s车辆密度最大的区间，最大路由跳数为10的实时路由跳数大于最大路由跳数为20时的实时路由跳数；在450～600 s之间，车辆密度稍降时，最大路由跳数为20的实时路由跳数大于最大路由跳数为10时的实时路由跳数。这种现象是由于车辆密度和最大路由跳数均过大时导致了多跳转发的成功率降低，实际成功传输的数据包多为转发跳数较小的数据包。图9中的实时端到端延时整体随最大路由跳数的增加而增加，与直道场景结论一致。

图8 实时路由跳数Fig.8 Routing hop count in real-time

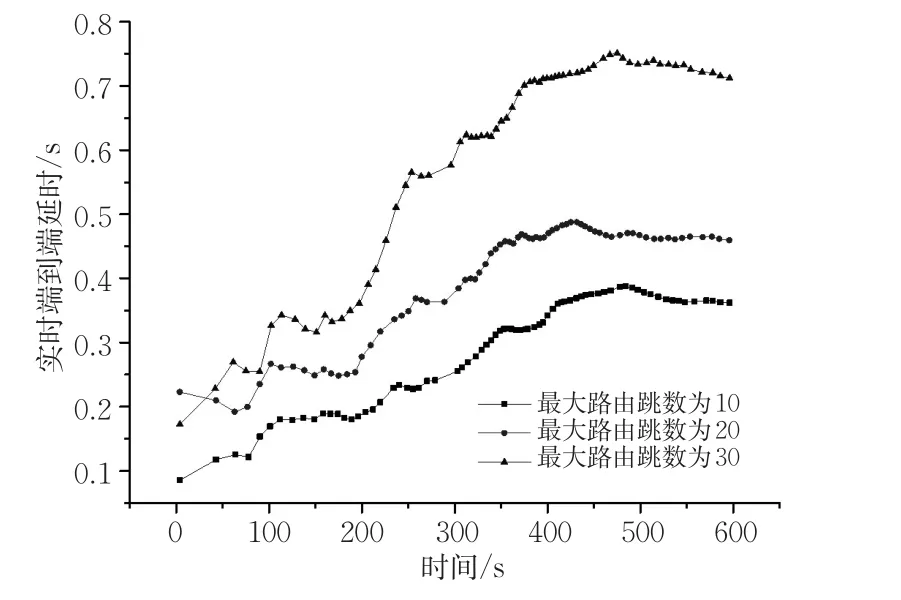
图9 实时端到端延时Fig.9 End-to-end delay in real-time

城市道路场景中所得的整体结论与直道场景基本一致，根据交通车辆密度选择不同的最大路由跳数能够进一步改善多跳车联网的通信质量，为智能交通和智能网联汽车的应用提供基础。

4 结束语

研究了在不同的车辆密度情况下，选择不同的最大路由跳数参数对车联网各项性能指标的影响。利用泊松分布模型，建立了最大路由跳数和车辆密度的节点连接性概率及数据包投递率模型。基于Veins仿真平台，分别对不同车辆密度下的直道场景和城市道路场景做大量仿真实验，并对数据包投递率、平均路由跳数和平均端到端延时做统计分析。仿真结果表明，同一车辆密度下，实验设定的几种不同最大路由跳数造成的包投递率差异在直道场景下最大可达约20%，在城市场景下最大可达约6%。根据不同的车辆密度选择其对应的最佳最大路由跳数参数可使得平均包投递率最高，并且越小的车辆密度通常对应于越大的最大路由跳数最佳数值。

在进一步的工作中可根据不同的车辆密度自适应选取最佳的最大路由跳数，作为车联网路由优化策略中的重要组成部分。在建立的数据包投递率模型及不同场景下的仿真研究时未考虑环境因素造成的物理信道等方面的差异，这在之后的工作中可展开进一步的深入研究。另外由于条件限制，文中的实验还停留在仿真阶段，在条件满足的情况下，可在车联网应用测试环境中进行测试。