考虑个体停车需求的医院泊位分配优化*

孙 博 焦朋朋 张羽佳

（北京建筑大学北京未来城市设计高精尖创新中心 北京 100044）

0 引 言

土地可利用资源有限的前提下，小汽车数量飞速增长造成极大的停车压力，医院作为保障生命健康的重要场所，其停车问题尤为突出。因此，最大化提高医院停车位的使用效率，有序化医院停车布置调整需求，满足不同类别就医者的停车需求成为亟需解决的问题。

近年来，停车问题研究多集中于停车需求预测、停车诱导和停车位优化。从停车需求预测进行分析实证的有：冉江宇[1]对停车需求的动态分布特征进行阐述；Yu Jingfei等[2]分析停车需求预测的必要性和阐述停车需求预测模型的发展过程，选择机动车OD法预测停车需求；Hyeonsup Lim等[3]考虑共享停车和停车需求的时间分布，建立基于广义时间成本的停车需求预测模型并进行灵敏度检验；Xiao等[4]基于排队论模型，建立包含停车参数估计的停车设施占用率预测模型。从停车诱导进行研究的：刘建明等[5]基于Stackelberg多轮博弈的原理，构造停车诱导系统与用户之间的博弈模型；Sarangi等[6]提出并验证最小化定位误差的停车策略；Muhammad Alam等[7]基于磁性和视觉传感器，设计智能交通构架向特定区域内的驾驶员提供关于空置停车位信息；Nazia Bibi等[8]基于视觉的智能停车框架建立了停车诱导模型。从停车位优化进行分析论证的：段满珍等[9]对于路网区域停车，提出面向个体的停车诱导配模型；Adam Wenneman等[10]研究了距离衰减加权回归估计模型，量化非法商用车停放、停车供需关系；陈峻等[11]以提升停车场泊位使用率为目标，建立高校共享泊位分配的双层模型；肖婧等[12]提出综合用户出行前后的高维多目标停车场选择及路径诱导模型，并通过高维多目标优化算法 KS-MODE求解。

目前，研究大多集中于在全路网范围内为驾驶员提供停车诱导信息，对于就医类驾驶员的个体需求特性及停车泊位选择的随机性研究较少，几乎没有对特殊功能用地按需求进行泊位分配的精细化设计方案。笔者以实体大型医院为例，充分考量不同泊位使用者的停车需求主观性，基于医院停车人群不同需求，兼顾停车场管理者的效益，建立泊位动态分配优化模型，调节停车需求，实现有序合理的泊位规划，使得社会效益最大化，为缓解医院停车难问题提供策略。

1 医院停车需求程度分级

将医院停车人群按需求归为7类[13]，主要包括：急诊人群、门诊人群、检查人群、探望人群、上班人群、住院人群和其他人群。从定性角度分析，对于急诊人群，其停车需求较为刚性，应保证车辆到达时有充足便捷的停车位。对于门诊及检查人群，其停车需求的紧张程度与病情急缓程度成正比，期望停车位置距就诊目的地越近越好，在医院正常工作时间内，医院整体规模愈大，停车需求量同比例增加。对于探望人群，其停车需求量随住院人群数量波动。而上班人群的停车需求量集中于医院的正常工作时间前，随医院内部不同员工停车政策产生的停车需求量不同。

按照到达医院目的不同，泊位使用者对停车需求不同，急诊人群停车需求紧迫程度为A级，泊车优先级最高，门诊人群停车需求紧迫程度次之。西安市红会医院为三级甲等大型医院，日门诊量为4 400人次，选取周一、周三对各类人群停车紧迫程度和时空需求定量调查，结果表1。

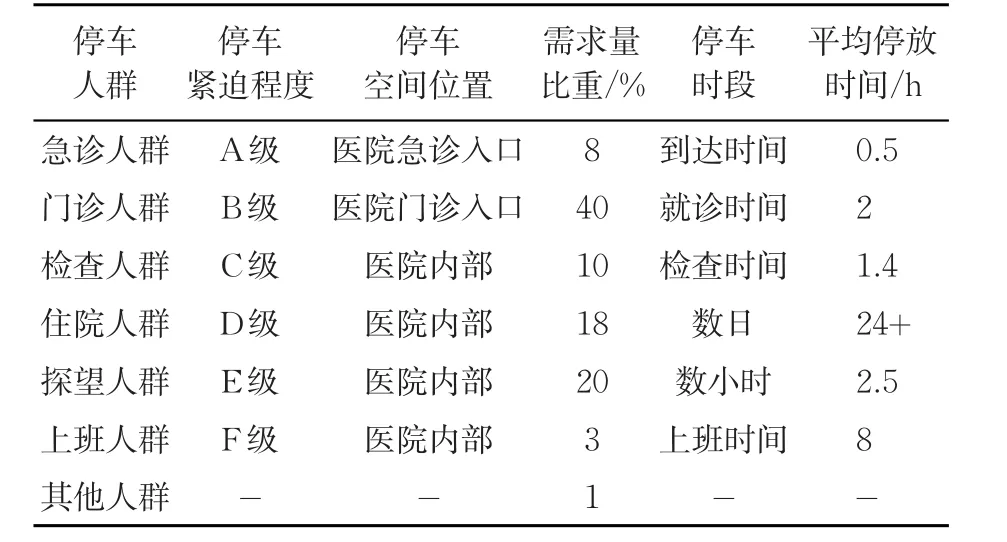
表1 各类人群停车时空需求Tab.1 Parking space requirements for all kinds of people

由表1统计结果分析可知，急诊人群的紧迫程度最高，为医院停车的首要服务对象。门诊人群停车紧迫程度次之，二者停车地点倾向于急诊或门诊入口。门诊人群需求量最大，为医院停车的主要服务对象。门诊人群、检查人群和探望人群的停车时段稳定且平均停放时间较短，停车流动性较大，为医院停车的重点服务对象。

因此，基于医院停车人群需求类型的差异性，建立高效的泊位分配方案，合理布置各类人群的车辆存取位置极为必要。

2 模型的建立与求解

医院停车场决策者期望分配方案在保障停车场收益的情况下达到社会效益最大化，而该方案依赖于各类个体需求的最优分配方案。同时，个体最优分配的方案受决策者最优分配方案的制约，属于双层递阶结构的系统优化问题[14]。本模型旨在对医院停车人群需求中，关键的可定量因素进行量化并优化，以期使得各类来往人群的停车需求得到最大化的满足，停车场的社会效益达到最优。

2.1 模型建立

将医院停车区域按相邻建筑属性划分成i个小区i=(1,2,…,n)；Pi为每个小区的命名；Ci为每个小区的停车最大容量（单位：辆）；用集合I={P1,P2,P3,…,Pn}表示医院内停车小区的集合；χ为分区密集程度，即主要需求类型小区的个数，本模型以门诊人群作为主要需求。

K为所有停车个体的集合，G为所有停车需求的集合；假设某一种需求下有 k(k=1,2,…,j)个个体同时到达医院；Kn∈K为第n种需求下停车个体的集合；J为对每个个体生成停车方案的集合；系统根据个体信息属性并结合对应小区内当前容纳车辆数Ni；为每个个体生成匹配方案Mij（第i个小区，第 j个方案），个体选择接受或拒绝系统方案。考虑费用对停车的吸引，按停车紧迫程度高低对车辆进行停车费用管理，紧迫程度较低，则停车收费标准τHx较高；反之停车收费标准较低，个体有权拒绝收费标准过高的分配方案，则该方案无效。

各停车小区内泊位使用情况以停车场集中指数yi反映，对小区样本的停车集中指数取方差；记λi=D(Y)为高峰时期整个停车场的使用效率，λi越小，说明各小区停车集中指数越接近，各小区停车饱和度相近，小区划分较为合理，满足各类人群的停车需求。

按递增排序 y1＜y2＜y3＜…＜yi，当 yi趋近于1时，该停车小区停车接近饱和，则安排个体按停车紧迫程度由低等级（E级）停车区域向高等级（A级）停车区域依次蔓延泊车，停车管理难度在车辆按区停放的基础上，与小区内车辆数、蔓延小区等级的跨度差成正比，引入停车管理指数Ω反映。

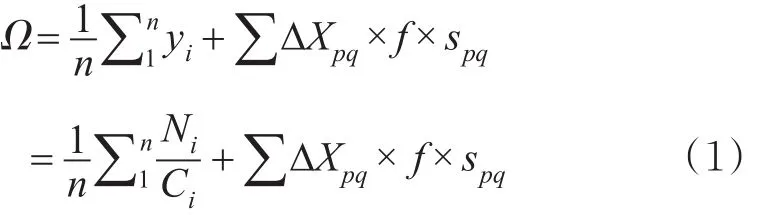
式中：p为量化后实际停车小区等级；q为量化后理论停车小区等级；ΔX为小区等级 p,q的差值；f表示难度系数，与停车跨度正相关；spq表示跨等级pq停车的个体数量，辆。

鉴于用地资源紧缺的问题，应合理充分利用停车场资源，对不同紧迫度的停车需求执行不同的收费标准，按既有划分的停车需求小区进行收费管理，规定停车场管理者的收益定义为F

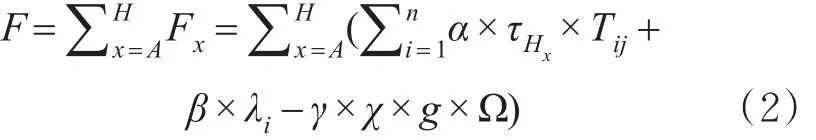
式中：Fx为某一个体需求下对应的停车场管理利益；Tij表示个体在Pi小区的停车时间，h；g为停车场管理费用，元；Ω为停车管理指数；α×τHx×Tij表示i小区内第 j个停车方案在停车时间Tij内应收取的停车费用，元；β×λi表示停车场使用效率；γ×χ×g×Ω为停车管理成本，元；α,β,γ为系数。

为避免单纯的追求高利润而造成现有停车资源的浪费，以10 min为间隔对等待个体需求进行1次筛选，按需求紧迫程度从高到低、综合考虑停车场管理者利益与停车系统中个体逗留时间成本进行泊位分配，以实现社会效益最大化，规定社会效益Y为

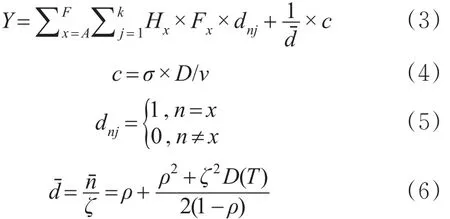
式中：Hx表示个体需求；Fx为该需求下，对应的停车场管理者利益；dnj为0-1变量，当个体实际需求紧迫程度与泊位分配方案相同时，取dnj=1，反之，dnj=0 ；dˉ为个体在系统中的平均等待时间，h；nˉ为系统中的个体数，辆；ζ为个体平均到达率，辆/h；ρ为服务强度；D(T)为个体服务时间的方差；c为逗留时间成本；σ为逗留过程中的单位时间成本；D为逗留过程中的行走距离，km；v为逗留过程中的平均速度，km/h。参照北京收费数据及车辆参数[15]，σ 取25元/h，v取10.8 km/h。

从停车场管理角度，考虑不同需求区域的收费标准、跨需求区域停车的管理对上层模型目标函数修正，兼顾管理者期望，在最大限度满足各类个体需求的条件下，停车场资源能得到充分利用且收益较大以保证社会效益最大化，进而确定各区域的停车方案 Wi。故上层模型为

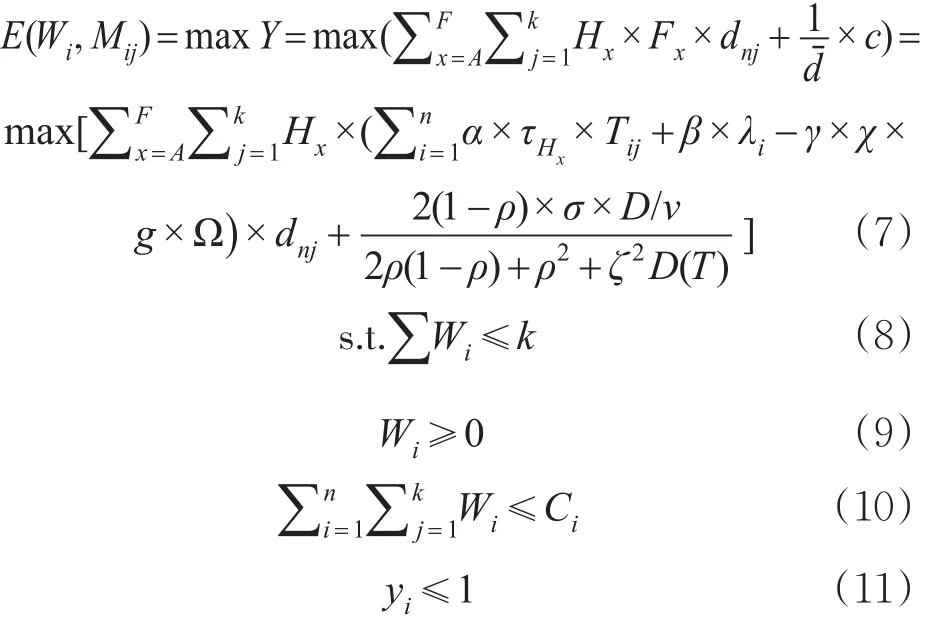
式（7）为目标函数，表示社会效益最大；式（8）表示方案数与个体数约束，系统最终生成的总停车方案不大于所有需求的停车个体数；式（9）表示按需分配，每个有需求小区的停车方案非负；式（10）表示方案数与停车小区容量的关系，对于每个小区生成的所有方案数不超过该小区的停车能力Ci；式（11）表示各停车小区容量限制，每个小区无停车溢出。

下层模型在规定停车区域内为个体推荐停车小区，引入选择模型对个体选择效用最佳的方案进行刻画。传统Logit选择模型仅研究可直接观测的显变量对选择结果的影响，如年龄、性别、收入、职业、是否为患者等个体特征变量，停车目的、停车时段、停车时长、周停放次数、停车区域步行距离等停车方案特征变量，停车费用、停车方式、停车位数量、是否与周边共享等停车场外部特征变量，此类变量作为通过现场调查或问卷调查直接获取的显变量。而实际医院停车过程中存在紧迫性、便捷性、合理性和环境舒适性等潜变量对个体的选择行为也会产生影响[16-17]。传统模型更注重选择的结果，在方案选择时无法体现与出行相关的潜变量，而对于医院类停车方案选择，个人态度、感受等潜变量对结果影响较大，SEM可以处理多个变量之间关系的社会科学验证性，包括回归分析、因子分析、潜变量关系等，更适用于用户出行偏好感知[18]，基于此本文通过构建SEM-Logit结构方程模型，充分考虑个体需求多样性，以满足实际案例中的停车需求问题。

医院不同停车人群由于停车紧迫程度和时空需求不同，对泊位选择具有需求差异性，除停车人群特征变量和停车方案特征变量外，本文引入停车方式、停车缴费方式、停车位数量、是否与周边共享等停车场外部特征变量，从需求侧对方案选择效用函数改进为

式中：j为选择方案；k为需求类型为Gx下的个体；r表示个体特征变量个数；m表示停车方案特征变量个数；l为停车外部特征变量个数；μGxjrk表示需求类型为Gx个体特征变量；γGxjmk表示需求类型为Gx停车方案变量；λGxjlk为需求类型为Gx停车外部特征变量；βGxjhk为需求类型为Gx个体关于第 j种停车方案的第h个潜变量aGxjr为Gx需求类型下个体特征变量对总效用的影响系数矩阵bGxjm为Gx需求类型下停车方案特性显变量对总效用的影响系数矩阵cGxjl为Gx需求类型下停车外部特征变量对总效用的影响系数矩阵dGxjh为Gx需求类型下停车内部特征潜变量对总效用的影响系数矩阵。

假设个体k的方式选择方案集合为Qx；可供选择方案 j的效用为Ujk；选择方案i'的效用为Ui'k；分析中引入二值变量Djk表示个体k的决策行为，通过结构方程模型建立各类变量之间的关系，模型具体表达形式见式（13）～（15）。

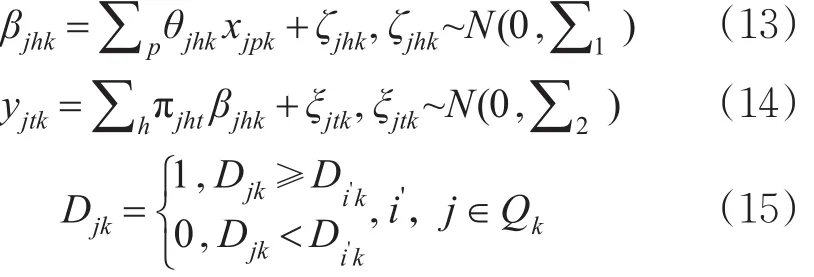
式中：p为显变量与潜变量具有关系的数量；h为潜变量数量；βjhk为第k个个体对于第 j个泊位分配方案的第h个潜变量；xjpk为与潜变量具有关系的显变量；θjhk为潜变量与相应观测变量之间的载荷因子；ζjhk为潜变量与相应观测变量的误差变量；yjtk为潜变量对应的观测变量；ξjtk为潜变量与显变量的误差变量；πjht为潜变量与显变量之间的载荷因子；Djk为个体对泊位分配方案的选择结果，Djk=0表示个体k不选择方案 j,Djk=1表示个体k选择方案 j。

个体选择方案 j的概率事件为Qx中所有泊车方式选择方案的最大效用值，假定效用函数的随机误差项 εjk服从 Gumbel(ε～Gumbel(0,μ))分布，基于需求分类的Logit行为选择模型为

个体可承受的最大时间成本为ξij由可接受最大步行距离为Lij（单位：m）和就诊紧急度φH(0＜φH＜1)决定，其中，就诊紧急度φH由个体到达后可接受的最大等待时长与该个体就诊紧迫性决定，H={A,B,C,D,E}为停车紧迫程度的集合，a，b为系数，不同需求下个体的时间成本可表示为

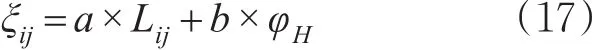
个体到达后可接受的最大等待时间由非生灭过程排队模型计算得到，个体到达服从泊松分布，停车服务时间与不同需求个体车辆停放位置有关，由此获得就诊紧急度φH为

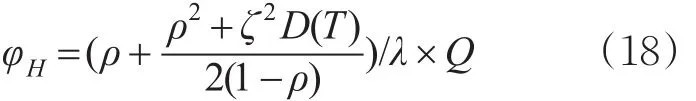
式中：Q为停车紧迫程度H中对应等级的量化值。

从个体角度，考虑不同需求人群停车的紧迫程度不同，可接受的时间成本不同导致停车方案选择不同，基于此对下层模型目标函数进行刻画，系统根据个体需求特性生成多个停车方案，停车泊位分配遵循个体效用函数，最大程度满足各类个体的停车需求进行泊位分配。下层模型为

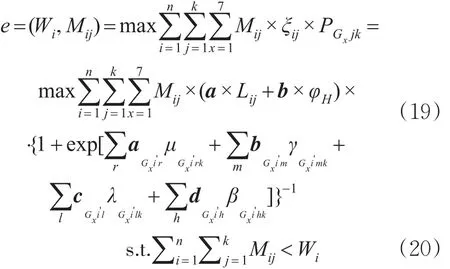
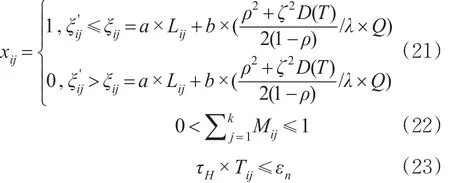
式（19）为目标函数，表示为不同需求个体分配其时间成本最小的方案；式（20）表示第i类人群的停车需求量不大于系统最终生成的停车方案数；式（21）表示个体接受与否，个体接受停车方案xij=1，否则放弃该方案；式（22）表示个体同一时刻只能选择一种停车方案；式（23）中，εn为第n种需求下停车个体可接受的平均停车费用成本（单位：元），表示每个用户的实际停车费用成本不大于该用户需求类型下的期望费用成本。

模型基于智能停车系统获取的个体需求特征数据和停车场泊位数据，通过对个体需求的系统化归类处理，化混乱停车为有序停车，从需求侧对停车需求分区诱导并管理，缓解医院停车供需矛盾，实现社会效益最大化。停车场泊位实时分配流程图见图1。

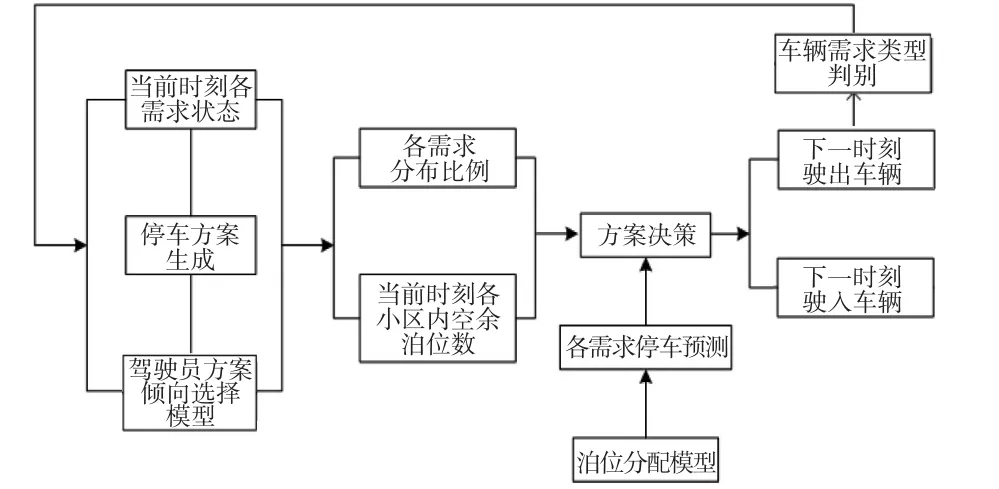
图1 停车场泊位分配流程图Fig.1 Parking lot berth allocation flow chart

2.2 模型求解

上层模型根据下层模型重新给出的停车分配方案，对停车分配方案进一步优化，选择最优方案对不同需求车辆分区停放。通过对模型分析，借鉴模拟退火算法[19]，对该模型进行优化算法求解，求解流程见图2。

步骤1。智能停车管理系统初始化，获取当前停车场各小区的初始车辆数N1,N2,…,Ni，并计算停车集中指数 y1,y2,…,yi，停车费用τH，以及整个停车场的初始使用效率λ0和初始停车管理指数Ω0，并代入下层进行求解，得到对于每个个体的分配方案e0，通过停车场管理者利益F重新计算得到停车场泊位分配方案E0。确定内层循环次数i，给定初始温度T0和终止温度Tz，令外层循环次数j=0，Tn=T0。

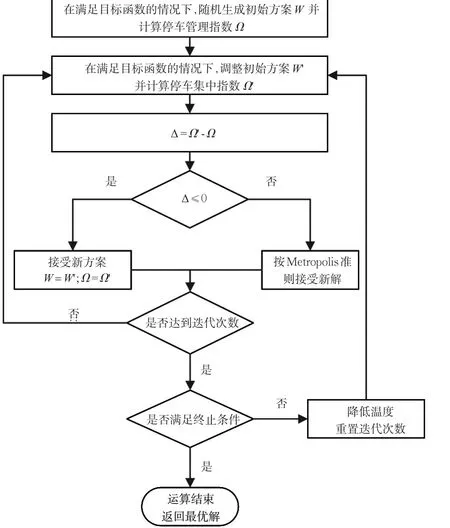
图2 模拟退火算法求解流程图Fig.2 Simulated annealing algorithm solution flow chart

步骤2。对温度Tn确定内循环次数n，产生新的状态，根据停车场的初始使用效率λ'，将其代入下层模型进行求解，得到新的个体分配方案e'，结合停车场收益、各区泊位使用情况以及跨区泊位蔓延情况，计算得到停车管理指数Ω'。

步骤3。令Δf=Ω'-Ω ，若Δf＜0，接受该泊位分配方案Wi；若Δf＞0，根据Metropolis准则判断是否接受。若n=i，转至步骤4；否则n=n+1，转至步骤2。

步骤4。判断是否终止。若Tj＜Tz，算法终止，根据此时停车场管理指数Ω，确定最优分配方案Wi；否则进行降温，降低Tj，j=j+1，转至步骤2。

3 案例分析

3.1 调查数据

以西安市红会医院作为实际研究案例，对模型进行验证研究。医院平面布局见图3。

结合相邻建筑物属性，以个体需求为依据划分的停车小区空间拓扑关系见图4。小区1主要服务上班人群，小区4主要服务住院人群，小区5主要服务探望人群，小区2，3，6主要服务就诊人群并分别对应检查人群、门诊人群和急诊人群。当某一小区停车饱和时，按需求紧迫程度等级由低至高向相邻小区蔓延停车。

选取工作日（周一、周三）和非工作日（周六）对红会医院停车进行连续3周的重复现场调查，通过现场和网络的形式发放停车调查问卷，3周累计发放问卷632份，共成功收回问卷608份，回收效率达96.2%，有效问卷为529份，有效率达83.7%，问卷变量设计见表2。

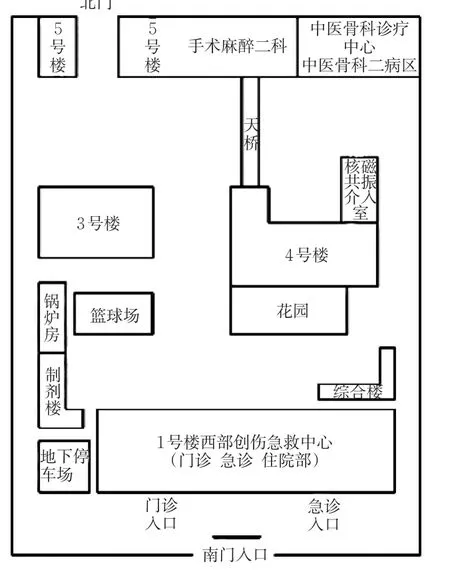
图3 医院内各主要建筑分布图Fig.3 Distribution map of major buildings in the hospital

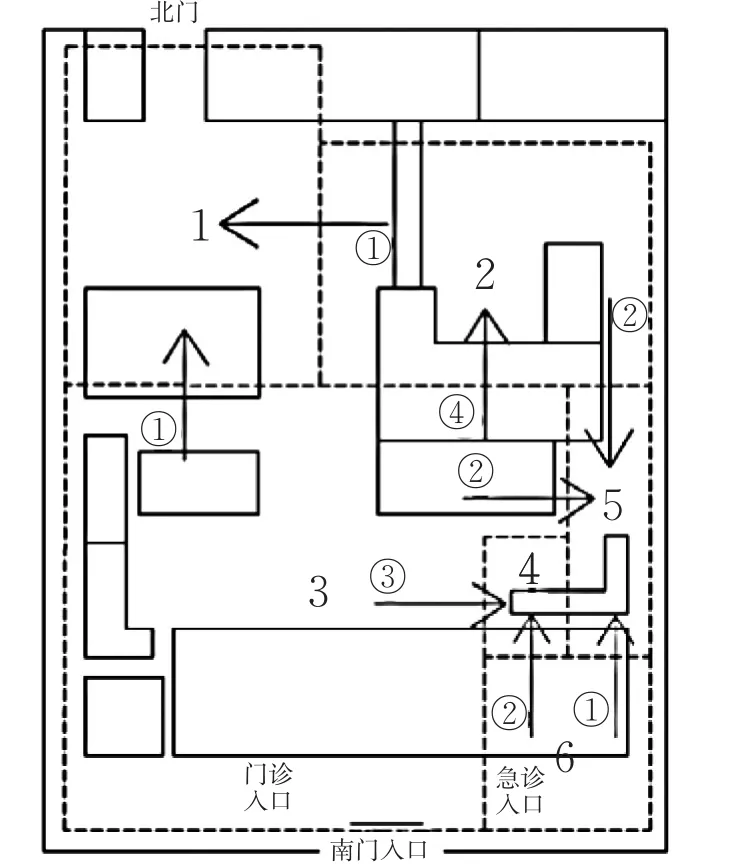
图4 停车小区搜索实例Fig.4 Parking area search example

表2 停车问卷变量设计Tab.2 Parking questionnaire variable design

基于调查数据建立进行结构方程模型，由AMOS计算得到结构方程的参数估计值，剔除无关变量，整理得到的标准化修正模型参数标定结果见表3。

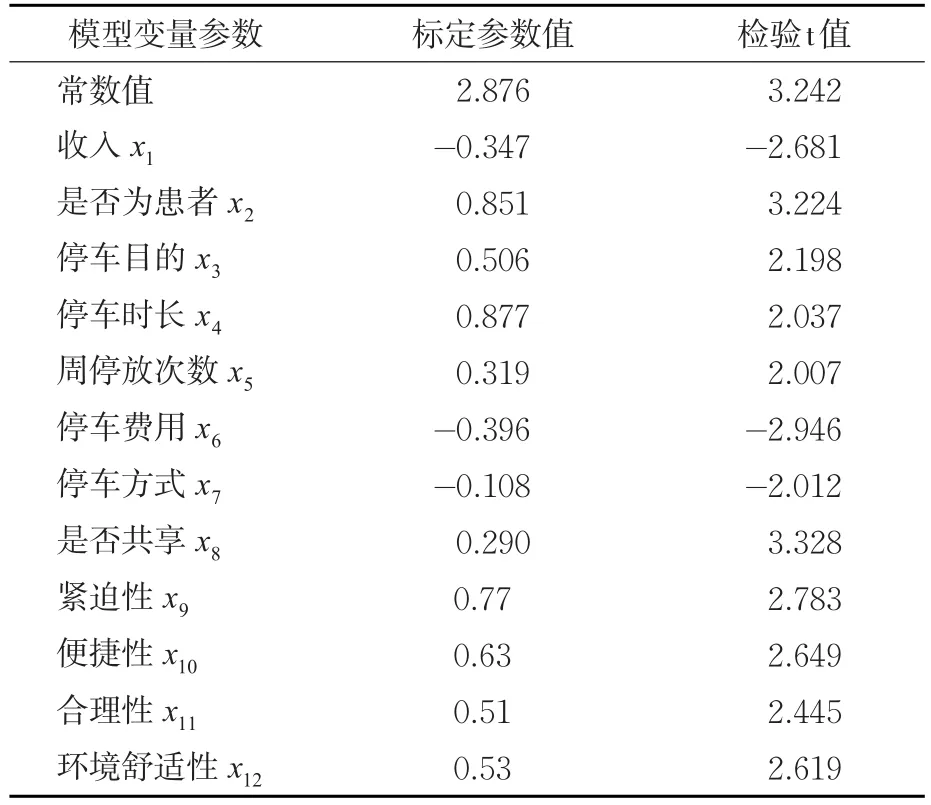
表3 标准化修正结果方程模型参数标定结果Tab.3 Standardized correction result equation model parameter calibration result

对问卷结果进行分析，将门诊人群、急诊人群和检查人群统一归为就诊人群。就诊人群、探望人群、上班人群和住院人群的平均单位期望成本为8元、5元、2元、1.5元；考虑停车个体对时间成本的倾向度，模型中a取0.4，b取0.5。

3.2 优化效果分析

本模型以智能停车系统为应用背景，在智能停车设备完善的情况下，通过医院出入口电磁线圈，可获取医院内车辆数，按小区对停车场监控，可获取小区内车辆变化情况。针对大型医院，其停车出入口与主要就诊楼相连，包括门诊楼、检查楼、住院楼等，以就诊楼服务功能作为按需求划分小区的标准。通过摄像头捕捉车牌照和驾驶员信息，按出现次数及位置进行需求归类。为便于对比分析，仿真时段内的个体数k采用连续周一调研数据的均值（服从泊松分布），数据采集时间间隔10 min，车辆停放时间服从Gamma分布。为对比在个体总数不变的条件下，停车场分配模型在城市停车管理方面的效果，利用Matlab软件对医院停车过程进行模拟仿真，仿真时段为00：00—23：00，迭代步长为1 h，计算得到医院停车相关指标。

停车管理指数高峰时期见图5，停车管理指数在高峰时期处于比较稳定的状态，均小于1，随停车场内车辆数有轻微浮动，停车场管理难度处于可接受范围内，认为分配方案可行。

优化前后1 d内停车场车辆数变化见表4，重新分配后2个停车峰值各后移1 h，分别由10：00和15：00后移至11：00和16：00。早晚峰值得到有效缓解，上午高峰峰值从265辆降至239辆，下午高峰峰值从253辆降至227辆，分别降低了9.8%和10.3%，在医院内车辆总数几乎未变的情况下，减少最高峰时刻医院内车辆数，使得高峰时段车辆数基本稳定在医院可容纳车辆数内，基本无车辆溢出现象。

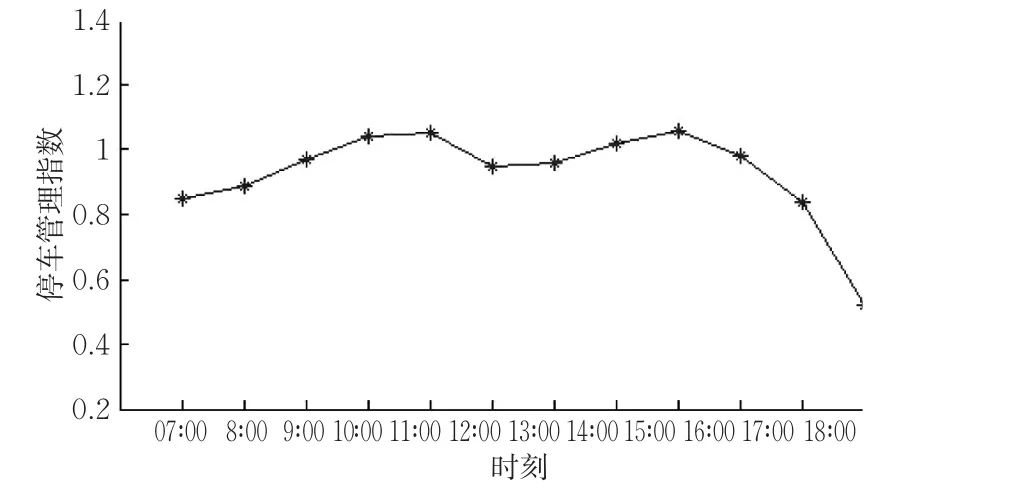
图5 停车管理指数Fig.5 Parking management index

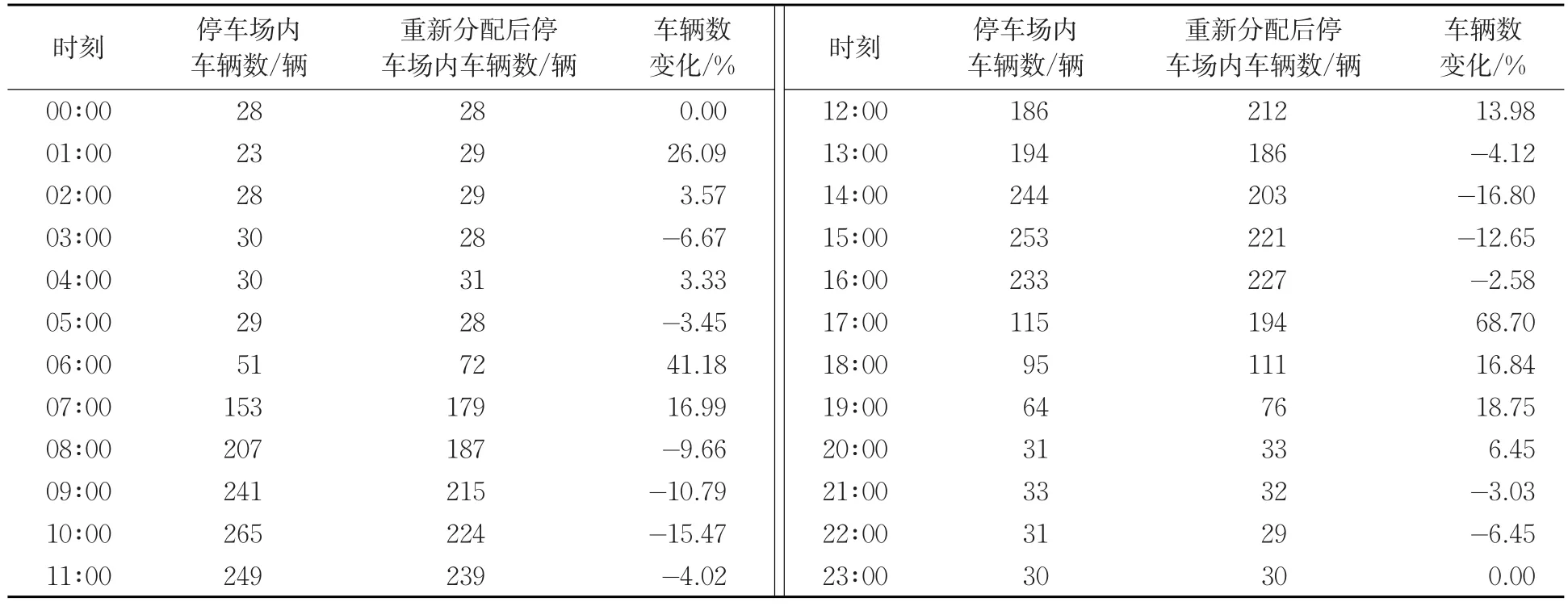
表4 1天内停车场内车辆数目变化Tab.4 The number of vehicles in the parking lot changes in one day

医院入口排队长度高峰时期重新分配前后对比见图6，排队长度明显减小，特别是高峰时期最大排队长度由13辆降至8辆，降低了38.5%，极大提高了医院入口处车辆的通行效率。

在07：00—18：00时段内，对停车场内每个停车位车辆停放次数统计，得到重新分配前后各车位停放次数的累计频率图，见图7。重新分配前大部分停车位停车3～7次，7.83%的停车位停放车辆次数大于10次，重新分配后大部分停车位停车5～10次，28.36%停车位停放车辆次数大于10次。医院停车场内泊位周转率明显增加，服务车辆数明显增多，停车场使用效率提高。

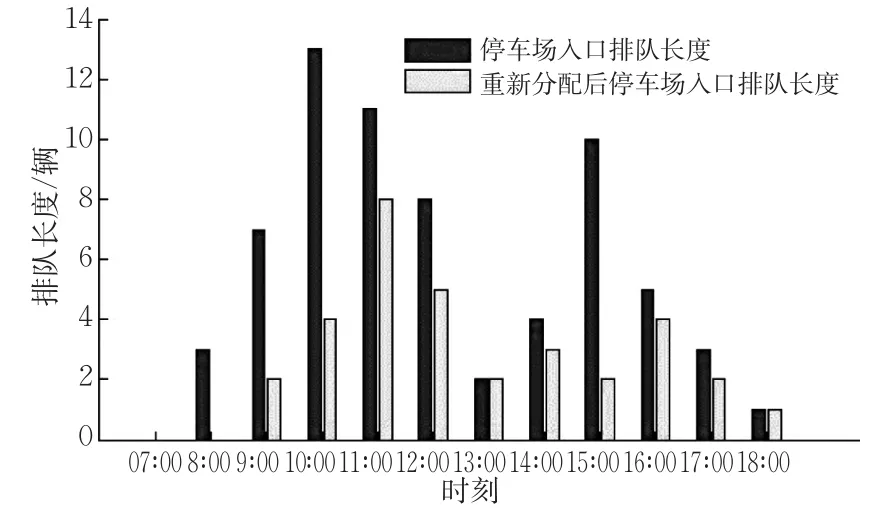
图6 停车场入口处排队长度Fig.6 Queue length at the entrance to the parking lot

优化模型仿真结果表明，考虑个体需求重新分配停车泊位的停车方案有效提高停车管理稳定性，极大程度满足各类个体的停车需求，同时提高车辆停放的有序性及停车泊位的利用率，保障高峰时段停车场内泊位均衡。

3.3 模型有效性分析

以各小区中需求量最大的小区作为主要需求类型小区，以分区密集程度χ来反应这种变化。将分区密集程度χ分别设置为1，2，4进行灵敏度分析。通过对比不同χ值下停车场使用情况和社会效益，可得出最佳分区密集程度，见表5。

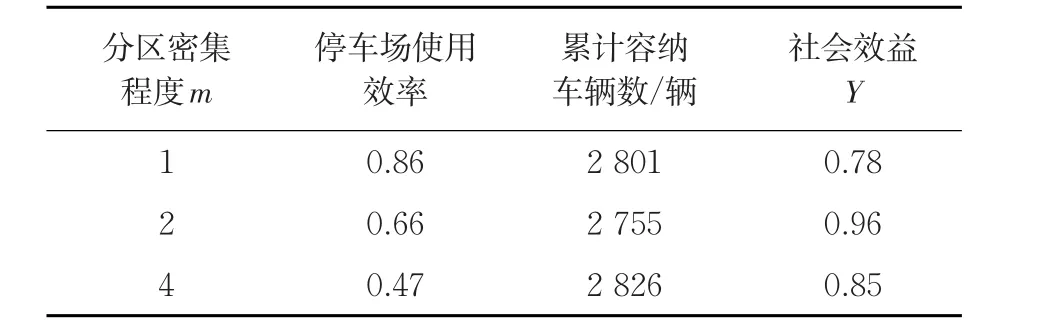
表5 不同χ条件下停车场使用情况Tab.5 Parking lot usage under differentχvalues

由上表可知，在分区密集程度分别为1，2，4时，Ci值逐渐减小，停车场使用效率提高，而社会效益先增加后减少，在χ=2的时候最大。分区密集程度为4的时候，停车场使用效率最大，说明对相同需求分区多而分散在一定程度上可以提高停车场的使用效率，但对停车管理产生一定压力，分区密集化不是最有效的选择。因此，分区密集程度χ=2时，停车场使用效率为0.66，为最佳泊位分配方案，此时社会效益达到最大0.96。

该模型根据医院停车人群需求特性进行分区分配泊位，很大程度上缓解了医院供需不平衡的问题，在停车管理指数基本平稳的前提下，削弱上午和下午高峰停车的车辆数，使得高峰时期系统中个体停车效率提高，累计停车频率增加，泊位分配模型为不同需求个体分配更具针对性的方案，保障停车场的社会效益。有效性分析显示，在分区密集程度影响模型稳定性，分区越密集，停车场使用效率越高，而在χ=2时社会效益最大，说明模型精度有待进一步优化。

4 结束语

本文建立了由管理层和用户层组成的停车泊位分配方案，可以结合停车人群需求的变化和停车场泊位的时变规律供给策略，以已知的固定分区确定初始解，并结合模拟退火算法求解，实现按个体需求的动态泊位分配。

改进了包含不可观测潜变量的SEM-Logit模型，考虑个体特征、停车方案特征和停车场外部特征，综合定量化描述停车行为选择过程，服务不同个体需求泊位分配优化。基于实例分析可知，将医院停车人群进行需求划分后，进行泊位按需配置，有助于减少个体泊车的随机性，减少就医停车时间，有序化停车的管理，有助于提高泊位利用率，达到了“削峰填谷”的作用。在合理分区的情况下停车场社会效益可达到最优，证明该模型在停车管理中有很强的实际应用价值和参考意义。下一步可对不同需求个体的停车分区界定进行深入研究讨论，本模型采用定区定收费标准，对于收费标准分时段变化的情况仍可做进一步分析。