基于卡尔曼-高斯联合滤波的车辆位置跟踪*

高 策 褚端峰▲ 何书贤 贺 宜 吴超仲 陆丽萍

(1.武汉理工大学智能交通系统研究中心 武汉 430063；2.武汉理工大学水路公路交通安全控制与装备教育部工程研究中心 武汉 430063；3.武汉理工大学计算机科学与技术学院 武汉 430063)

0 引 言

车辆卫星定位能够为车辆提供实时、准确的位置信息，为车辆服务提供了基础。随着智能网联汽车技术的发展，对车辆定位提出了更高的要求，车辆的精准定位也成为了当前研究的热点。

目前，车辆卫星定位的精度一般在10 m左右[1]。为了提高车辆卫星定位的精度，卡尔曼滤波和粒子滤波是2种常用的定位滤波算法。早期的卡尔曼滤波只能适用于线性系统[2]，但卫星定位系统是非线性的，这就导致了研究非线性卡尔曼滤波算法的必要性。一般使用卡尔曼滤波算法时，噪声的统计特性是难以确定的，往往通过调参确定相对滤波效果较好的噪声特性，但是不能保证滤波的稳定性。为了解决噪声的统计特性问题，赵欣[3]提出了基于噪声统计特性自适应估计的滤波算法。C.Zeng等[4]使用扩展卡尔曼滤波进行GPS信号的高动态跟踪。田宠[5]针对卡尔曼滤波容易发散的问题，提出了带衰减因子的自适应滤波器技术，采用衰减的加权因子，使估计器逐渐忘记陈旧数据的作用，同时增加新数据的比重，避免滤波过程的发散。付心如[6]研究了一种观测噪声协方差和抗差自适应相结合的卡尔曼滤波算法，有效的解决了观测异常对组合定位的影响。H.Feng等[7]使用卡尔曼滤波器对车辆位置进行预测，并对卡尔曼滤波器的预测性能进行了分析。张园[8]针对定位中有色噪声的情况，通过增加似然分布自适应调整来改进粒子滤波达到目标跟踪的目的。Q Shen等[9]针对车载定位收到的不连续周期信号，应用相对于参考卫星形成差分定位算法进行定位优化。王琰[10]针对历元定位精度有时不如单一系统定位精度的问题，提出了卫星分群的抗差卡尔曼滤波算法，根据卫星类型分类构建方差膨胀因子，从而改善定位精度。

对于车载卫星定位系统，在开阔环境中，GNSS可以为车辆提供实时、精确、可靠的位置信息，目前的滤波算法也可以很好地对卫星定位过程中的噪声进行滤除，对于常规噪声，一般采用卡尔曼滤波或者以卡尔曼为基础的衍生算法进行滤波操作[11-13]；但是当车辆处于复杂的行车环境中时，例如高大建筑物遮挡、城市隧道等，卫星定位信号会受到严重的干扰甚至是丢失，无法提供精确、持续、可靠的车辆位置信息，严重影响到行车安全。

车辆在行驶过程中卫星定位信号受到较大干扰时，由于噪声的统计特性突变，造成了卡尔曼滤波等算法并不能起到很好的滤波作用，造成车辆定位误差较大。针对上述问题，提出基于动态阈值的联合滤波方法，对噪声突变的车辆漂移位置进行识别，并使用高斯过程回归进行真实位置预测，并结合观测值构建观测补偿量，使用含有动态补偿量的卡尔曼滤波进行车辆卫星定位的优化，实现车辆精准定位。

1 卡尔曼-高斯联合滤波模型

车载卫星定位在不同情况下受到的信号干扰强度显然是不同的，对于行车过程中卫星信号受到干扰较大的情况下，卡尔曼滤波不能很好的解决这一问题[14]。为充分利用车辆的速度、加速度及航向角等信息，提高车辆定位系统的时间和空间覆盖率以及增加定位系统的信息利用率，建立基于动态阈值的卡尔曼-高斯联合滤波模型，该模型不仅设置了与车辆状态信息相关的动态阈值，可有效地识别出行车过程中卫星信号受到较大干扰造成的车辆定位漂移点，还对车辆的历史轨迹信息进行有监督式学习，从而可以根据车辆的历史信息预测当前时刻的车辆真实位置，并结合真实观测值构建卡尔曼滤波观测方程补偿量。通过联合滤波模型可以滤除多种行车工况下的噪声信号，对于比较恶劣的情况下产生的漂移现象，也会有很好的滤波作用。基于卡尔曼-高斯联合滤波模型的车载定位优化算法见图1。

首先，使用与车辆状态信息相关联的动态阈值进行车辆位置漂移点的识别；然后，利用车辆历史轨迹信息进行高斯过程回归，对当前车辆真实位置信息进行预测；最后，使用预测值和真实观测值构建观测补偿量，通过在卡尔曼观测方程加入动态补偿量，进行车辆定位的联合滤波，从而提高车辆定位精度。

1.1 动态阈值计算

图1 车载定位优化Fig.1 Vehicle positioning optimization

车辆行驶过程中的轨迹是连续的，车辆下一时刻的位置信息与车辆当前时刻的位置及车辆状态信息是密不可分的。车辆下一时刻的位置可以通过车辆当前时刻的位置与车辆的状态信息推算得出[15-16]，所以同样可以使用当前车辆位置信息与车辆的状态信息判断下一时刻车辆位置观测值的准确性。当周期Δt足够短时，认为当前时刻的位置与前一时刻的位置关系具体见式（1）。

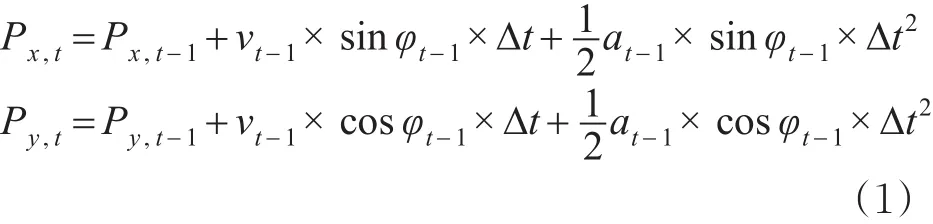
式中，Px,t为t时刻在东北天坐标系下东西方向上的位置，m；Py,t为t时刻在东北天坐标系下南北方向上的位置，m；vt-1为t-1时刻的速度，m/s2；at-1为t-1时刻的加速度；jt-1为t-1时刻的航向角（以真北方为基准），rad。

通过车辆位置信息和状态信息判断下一时刻的车辆位置信息的可靠性，从车辆卫星定位信息观测结果出发，设置与车辆速度及航向角等实时信息相关的动态阈值，使用动态阈值进行车辆卫星定位漂移点的识别。

动态阈值的设置与车辆当前的行驶状态信息相关，使用车辆位置推算的增量作为基本阈值，综合考虑信号干扰、速度以及加速度传感器误差的情况下，加入阈值增强因子l组成动态阈值，动态阈值公式见式（2）。

使用动态阈值可以判断车辆卫星定位信息是否可以信任，即在车辆卫星定位过程中是否产生漂移现象，判断依据见式（3）。

式中，Pt为t时刻车辆位置的实际观测值；Pt-1为t-1时刻车辆位置的实际观测值。

车辆当前位置实际观测值与前一时刻的位置之差的绝对值大于动态阈值时，可以认为车辆当前时刻定位信号不可信任，需要使用高斯过程回归进行车辆真实位置预测；该预测值结合观测值构建补偿量，通过在卡尔曼滤波观测方程中加入动态补偿量，达到联合滤波的目的。

考虑到车载卫星定位系统为动态定位，根据实车实验分析得出定位的精度跟车速密切相关，特别是当车速较低时，车载卫星定位精度较差，存在定位漂移现象，所以针对不同的车辆行驶状态，设置相应的阈值增强因子。根据反复的实车实验得知，当车速小于1 m/s时，λ取值为3；当车速大于等于1 m/s时，λ取值为1.5，动态阈值能够很好的识别车辆定位漂移点。

1.2 基于高斯过程回归的车辆位置预测

高斯过程基于贝叶斯原理，属于非参数概率模型，通过训练历史数据将先验分布转化为后验模型，通过后验模型得到具有概率意义的预测结果[17]。高斯过程回归是一种基于高斯随机函数的机器学习方法，主要利用样本进行学习来判断整个值函数的分布，对处理小样本、非线性等复杂问题具有很好的适应性。

利用车辆的历史轨迹信息作为学习样本进行高斯过程回归，样本的选取采用滑动窗口模式，随着时间的推移，窗口在学习样本上滑动，每1个周期内旧的样本被丢弃，新的样本被添加；为了减少计算量，更快地得到预测值，每次高斯过程回归的学习样本都是选取当前时刻之前的3个周期作为学习样本，进行核函数的参数优化，然后预测当前时刻的车辆位置。车辆位置预测过程见图2。

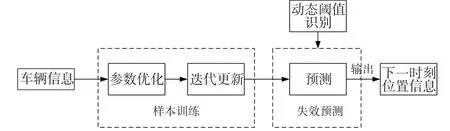
图2 车辆位置预测Fig.2 Vehicle position prediction

选取高斯核函数作为高斯过程回归的协方差函数，见式（5）。

根据高斯过程的性质，即学习样本跟预测样本符合同一分布的特点，可以得到学习样本和预测样本的联合分布。根据上面的协方差函数可以得到观测值与预测值的联合分布，观测值 y-3，y-2，y-1与预测值y的联合分布见式（6）。

其中，y-3，y-2，y-1为前3个时刻的观测值，y为当前时刻的预测值。

根据所得到的学习样本跟预测样本的联合分布可以得到预测样本的条件分布，见式（7）。

使用预测样本分布的均值作为当前时刻的预测值为

笔者并未对所有时刻的车辆位置数据都基于高斯过程回归进行预测，仅当车辆卫星定位数据不可以信任时，基于高斯过程回归进行车辆位置预测。因为车辆在行驶过程中具有一定的趋势性，当前时刻的位置一定跟历史轨迹相关[18]，所以使用车辆历史轨迹信息作为学习样本进行高斯过程回归然后预测当前时刻的车辆位置的方法具有一定的可靠性。

1.3 基于观测值补偿的卡尔曼滤波

普通卡尔曼滤波不能很好解决车辆受到较大干扰产生的漂移现象，原因是观测值中的噪声产生了突变，造成卡尔曼滤波无法有效滤波统计特性突变的噪声。针对车辆定位过程中噪声统计特性突变的情况，建立基于观测值补偿的卡尔曼滤波模型，状态量的选取见式（9）。

式中，e表示车辆在正东方向上的位置，m；n表示车辆在正北方向上的位置，m；v表示车辆的速度，m/s；h表示车辆的航向角（以正北方向为基准），rad；a表示车辆的加速度，m/s2；w表示车辆航向角的变化率，rad/s。

基于观测值补偿的卡尔曼滤波模型的状态方程跟观测方程见式（10）。

式中：Wk+1为过程噪声，该噪声为白色高斯过程噪声，均值为0，协方差为Q；Vk+1为观测噪声，该噪声为白色高斯过程噪声，均值为0，协方差为R；γ为观测值补偿量的系数，取值见式（11）。

ΔEk为观测值补偿量，见式（12）。

其中，ek，nk，vk，hk为车辆位置、速度和航向角的真实观测值为使用高斯过程回归进行的预测值。

基于观测值补偿的卡尔曼滤波可根据动态阈值的识别进行动态滤波。当动态阈值识别出车辆位置漂移点时，进行高斯过程回归，对车辆位置进行预测，通过预测值与真实观测值的差构建卡尔曼滤波观测方程的补偿量，从而应对定位过程中噪声统计特性突变的情况。

2 联合滤波过程

整个联合滤波过程均利用原始车辆数据及车辆状态信息，通过构建卡尔曼-高斯联合滤波模型进行车辆位置的滤波。首先，根据实时车速和航向角信息设置动态阈值，根据动态阈值结合上一时刻的车辆位置信息判断当前车辆位置是否为漂移点；然后，对动态阈值识别出的车辆卫星定位漂移点，进行高斯过程回归，使用车辆的历史轨迹信息作为学习样本预测当前时刻的车辆位置；最后，根据高斯过程回归的预测值和真实观测值构建卡尔曼滤波观测补偿量，结合动态阈值识别位置漂移情况，对卡尔曼滤波观测方程加入补偿量，从而实现卡尔曼滤波观测方程动态补偿，对车辆位置跟踪进行优化。联合滤波过程见图3。

图3 联合滤波模型流程图Fig.3 Flow chart of joint filter model

利用卡尔曼-高斯联合滤波模型进行实时动态滤波具体流程如下。

步骤1。计算当前时刻的动态阈值。通过当前时刻的车速与航向角等信息，计算出动态阈值。

步骤2。判断当前时刻的车辆位置与前1时刻车辆位置之差，是否超出动态阈值。若超出，则执行步骤3，否则直接执行步骤4。

步骤3。利用前3个时刻的车辆历史位置信息进行高斯过程回归的学习，再预测当前时刻的车辆位置信息，根据预测值和真实观测值之差构建观测补偿量。

步骤4。对卡尔曼滤波观测方程加入动态补偿，使用加入补偿量的卡尔曼滤波对车辆位置信息进行滤波优化。

步骤5。对每1时刻的车辆位置信息依次重复上述步骤。

3 实验验证与分析

3.1 实验方案设计

本文基于卡尔曼-高斯联合滤波模型采取实车数据验证，实验采用比亚迪e5电动车搭载某款OBU（on-board unit），板载的车载定位模块为u-blox M8模块，并搭载千寻RTK。实验路线选取武汉市太子湖附近的普通城市道路，车辆顺时针沿着车城北路、太子湖路、神龙大道、车城东路行驶，具体路线见图4。

图4 实验路线Fig.4 Route of experiment

为了更好地验证联合滤波对车辆卫星定位精度及可靠性的改进，实验中OBU与RTK设备同步采集车辆的卫星定位信息，周期都设置为0.2 s。RTK设备具有0.02 m的高定位精度，因此作为参考系统，其输出结果可近似作为汽车的实际位置信息即真值。采取对比实验验证，比较原始车辆卫星定位数据、普通卡尔曼滤波、基于动态阈值的卡尔曼-高斯联合滤波进行的车辆定位精度及可靠性。

3.2 算法验证与分析

通过实验采集的数据分析得知，车辆在行驶过程中，通过速度传感器得到的车速信息是可信的，车辆的航向角信息比较可靠。如图5～6所示，车辆在行驶过程中，车速与航向角信息随着时间比较平稳的变化，并没有发生较大的突变情况，所以采用车速信息与航向角信息作为动态阈值的设定依据比较可靠。

图5 车速信息Fig.5 Vehicle speed

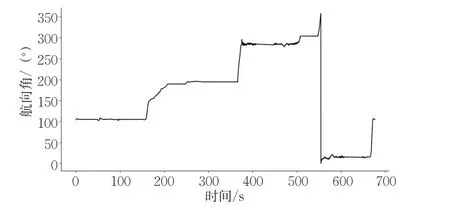
图6 航向角信息Fig.6 Vehicle heading angle

对于车辆在行驶过程中产生的卫星定位漂移现象，由于噪声统计特性的突变，导致常规的卡尔曼滤波不能很好地解决，滤波效果变差。基于动态阈值的卡尔曼-高斯联合滤波正是针对车辆卫星定位信号中噪声统计特性突变的情况，对于统计特性突变的噪声进行识别，然后进行联合滤波。普通卡尔曼滤波与联合滤波效果见图7。

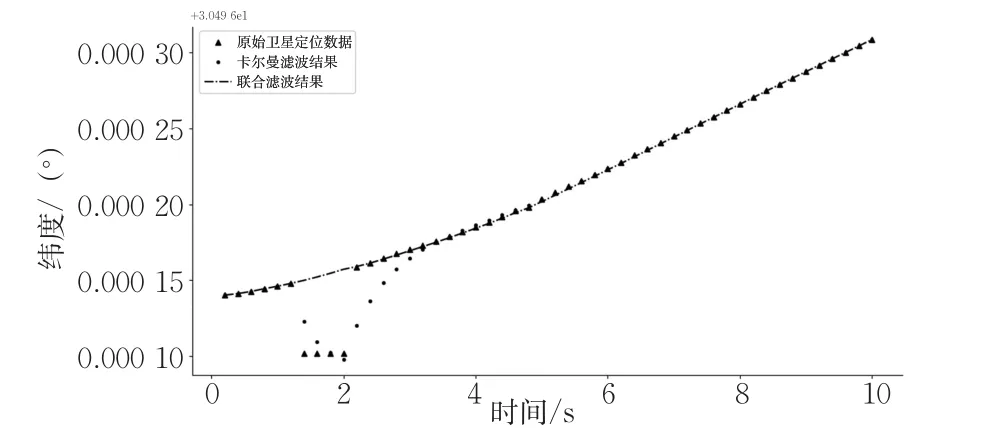
图7 联合滤波与卡尔曼滤波对比Fig.7 Comparison between joint filter and kalman filter

由图7可见，普通卡尔曼滤波对于卫星定位过程中噪声统计特性发生突变造成的车辆定位漂移现象的滤波效果不明显，而联合滤波是基于动态阈值识别车辆卫星定位漂移位置，并进行高斯过程回归处理，结合真实观测值设置动态的观测补偿量。对于易产生漂移现象的车辆定位，联合滤波效果明显好于普通卡尔曼滤波。

为了进一步验证算法的可靠性，选取了一段普通的城市道路，整个实验过程持续大约400 s，采样周期为0.2 s，全程共1 985条卫星定位数据，同时采集RTK数据作为车辆实际行驶轨迹的基准数据（即真值）。

图8 局部1联合滤波结果Fig.8 Part 1 of joint filter result

图9 局部2联合滤波结果Fig.9 Part 2 of joint filter result

整个实验过程中，选取了2处比较明显的车辆卫星定位漂移点，相对于RTK基准位置数据出现了较大的偏移。图8～9为2处存在卫星定位漂移点的车辆位置信息，图中黑色直线表示近似车辆实际行驶轨迹，三角形为车辆卫星定位原始数据。可以看到，受到较大干扰时，车辆卫星定位出现漂移现象，普通黑点为联合滤波之后的结果，可以从图8～9中看出，联合滤波对于定位噪声产生突变的车辆位置具有良好的滤波效果。

为了更加直观方便地观测联合滤波算法的效果，在卫星地图上绘制车辆原始位置信息以及滤波之后的轨迹，如图10所示，地标标记点为原始车辆位置数据，可以看到车辆位置受到干扰，位置产生漂移的车辆经纬度坐标，普通黑点标记为联合滤波之后的车辆经纬度坐标。根据联合滤波结果可以得出，联合滤波算法不仅对常规噪声有一定的滤波作用，对于车辆行驶过程中产生的较大的车辆漂移位置，可以很好地滤除。

图10 漂移点的滤波Fig.10 Filter of Drift Points

为了更好地证明联合滤波模型的有效性，对车辆的原始位置信息和联合滤波之后的位置信息做了数据对比分析。选取了图4实验中的一段数据作数据分析，其中包含了图8～9中的2段漂移信息，数据一共500个位置点信息。

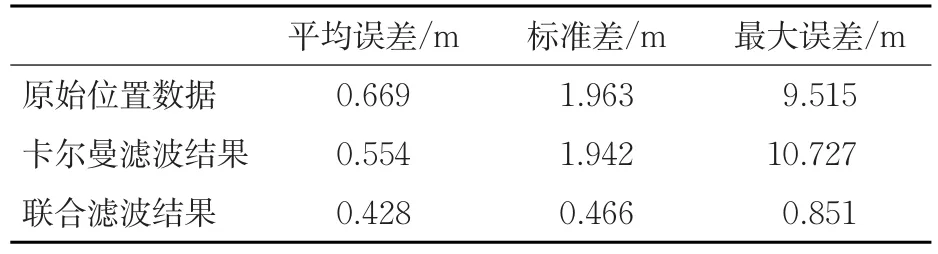
表1 滤波结果对比Tab.1 Comparison of filter results

表1为对比结果，从表1可以看出，卡尔曼滤波和联合滤波都对原始车辆卫星定位数据的精度有所改进。其中，平均误差反映定位精度，可以看出联合滤波的平均误差相对于普通卡尔曼滤波降低了大约0.12 m，定位精度提高了30%左右；联合滤波最突出的优点是可以有效滤除噪声突变引发的漂移点，最大误差由原始数据的9 m降低到0.8 m，可以反映联合滤波对漂移点的滤波效果；标准差也可以看出联合滤波对车辆定位位置漂移数据有很好的滤除效果。因此，联合滤波在提高定位精度的同时，可以有效识别并滤除车辆卫星定位漂移点，为车辆提供更加准确的位置信息，增强车辆定位的抗干扰能力。

相对于传统的车辆定位滤波方法，本文研究的联合滤波模型优点为：可以有效地识别并滤除卫星信号受到较大干扰时产生的车辆位置漂移点，在提高滤波精度的同时，也提高了车辆卫星定位的抗干扰性。

4 结束语

针对行车过程中卫星定位信号受到干扰产生的车辆位置漂移现象，建立了卡尔曼-高斯联合滤波模型，通过对车辆位置信息的实时滤波，提高了车辆位置信息的可靠性，增强了车载定位的抗干扰性。该模型从观测结果出发，通过设置与车速、航向角相关的动态阈值，识别车辆位置漂移现象，通过对车辆历史轨迹信息进行监督式学习，预测车辆位置，然后结合车辆位置真实观测值构建动态补偿量，通过对卡尔曼滤波观测方程中加入观测补偿量实现动态联合滤波。基于卡尔曼-高斯的联合滤波模型，可以有效识别出车辆定位漂移点，对于车辆卫星定位起到了很好的滤波作用。在现有低成本车载定位装置的情况下，有效提高车辆卫星定位的精度及可靠性。

研究尚缺少复杂路况对算法的验证，特别是存在城市隧道、高架桥等复杂且卫星信号干扰较大的路况；该算法主要利用车辆的历史轨迹数据进行有监督式的机器学习，还应结合道路信息，以此作为约束能更精确地确定车辆位置。